2018 IMO Problems/Problem 1
Contents
[hide]Problem
Let ![]() be the circumcircle of acute triangle
be the circumcircle of acute triangle ![]() . Points
. Points ![]() and
and ![]() are on segments
are on segments ![]() and
and ![]() respectively such that
respectively such that ![]() . The perpendicular bisectors of
. The perpendicular bisectors of ![]() and
and ![]() intersect minor arcs
intersect minor arcs ![]() and
and ![]() of
of ![]() at points
at points ![]() and
and ![]() respectively. Prove that lines
respectively. Prove that lines ![]() and
and ![]() are either parallel or they are the same line.
are either parallel or they are the same line.
Solution
http://wiki-images.artofproblemsolving.com/5/5d/FB_IMG_1531446409131.jpg
The diagram is certainly not to scale, but the argument is sound (I believe) and involves re-ordering the construction as specified in the original problem so that an identical state of affairs results, yet in so doing differently it is made clear that the line segments in question are parallel.
Construct a right-angled triangle ABC'. Select an arbitrary point H along the segment BC', and from point H select an arbitrary point F such that the segment HF is perpendicular to the segment AB. Mark the distance from the intersection of HF and AB to B at B" (i.e., HF is a perpendicular bisector). It follows that the triangle B"FB is isosceles. Construct an isosceles triangle FHG. Mark the distance of AB" along AC' at C". (From here, a circle can be constructed according to the sets of points A, B, F, and A, B, G. Points F and G may be repositioned to allow for these circles to coincide; also, point H may be repositioned so that point C falls on the coinciding circle, understood that HG is the other perpendicular bisector.)
Assign the angle BAC the value α. Hence, the angle FHG has the value 180°-α, and the angle HFG (also, HGF) has the value α/2. Assign the angle BFH the value β. Hence, the angle B'FB" has the value β-α/2. Consequently, the angle FB'B" has the value 180°-(β-α/2)-(90°-β) = 90°+α/2, and so too its vertical angle BB'G. As the triangle B"AC" is isosceles, and its subtended angle has the value α, the angles BB"C" and CC"B" both have the value 90°+α/2. It follows therefore that segments B"C" and FG are parallel.
(N.B. Points D and E, as given in the wording of the original problem, have been renamed B" and C" here.)
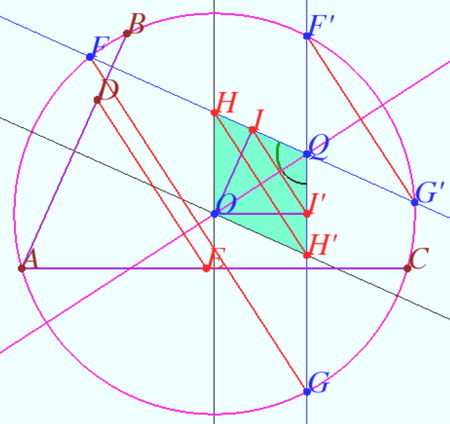
Solution 2
The essence of the proof is using a rhombus formed by the perpendicular bisectors of the segments ![]() and
and ![]() and the parallelism of its diagonal and the base of the triangle formed by the perpendiculars from one vertex of the rhombus.
and the parallelism of its diagonal and the base of the triangle formed by the perpendiculars from one vertex of the rhombus.
The perpendicular bisectors of the segments ![]() and
and ![]() intersect at points
intersect at points ![]() (the circumcenter
(the circumcenter ![]() and
and ![]() Let
Let ![]() The distance from the line
The distance from the line ![]() to point
to point ![]() is
is ![]() from
from ![]() to
to ![]() is
is ![]() Therefore, the distance between lines
Therefore, the distance between lines ![]() and
and ![]() is
is ![]() Similarly, the distance between the lines
Similarly, the distance between the lines ![]() and
and ![]() is
is ![]()
The quadrilateral ![]() is formed by the intersection of two pairs of equidistant lines
is formed by the intersection of two pairs of equidistant lines ![]()
![]() is a parallelogram with equal heights
is a parallelogram with equal heights ![]()
![]() is a rhombus.
is a rhombus.
Let ![]() and
and ![]() be the feet of the heights of the rhombus from the vertex
be the feet of the heights of the rhombus from the vertex ![]() In isosceles triangles
In isosceles triangles ![]() and
and ![]() the sides are parallel, hence the bases of these triangles are parallel,
the sides are parallel, hence the bases of these triangles are parallel, ![]() The feet of the heights
The feet of the heights ![]() and
and ![]() divide the sides of the rhombus in the same ratio, which means that the diagonal
divide the sides of the rhombus in the same ratio, which means that the diagonal ![]() of the rhombus is parallel to the segments
of the rhombus is parallel to the segments ![]()
The angles between the diagonal of the rhombus and its sides are the same, so ![]() The lines
The lines ![]() and
and ![]() are symmetrical with respect to the diameter
are symmetrical with respect to the diameter ![]() so
so ![]() The homothety of triangles
The homothety of triangles ![]() and
and ![]() centered at
centered at ![]() implies
implies ![]() Therefore, these three lines are parallel to
Therefore, these three lines are parallel to ![]()
Note that triangle ![]() may be obtuse.
may be obtuse.
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2018 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||