2022 AMC 10A Problems/Problem 25
Problem 25
Let ![]() ,
, ![]() , and
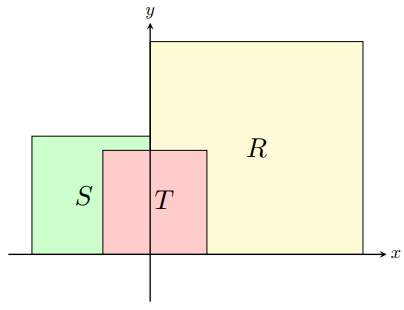
, and ![]() be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the x-axis. The left edge of
be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the x-axis. The left edge of ![]() and the right edge of
and the right edge of ![]() are on the
are on the ![]() -axis, and
-axis, and ![]() contains
contains ![]() as many lattice points as does
as many lattice points as does ![]() . The top two vertices of
. The top two vertices of ![]() are in
are in ![]() , and
, and ![]() contains
contains ![]() of the lattice points contained in
of the lattice points contained in ![]() . See the figure (not drawn to scale).
. See the figure (not drawn to scale).
The fraction of lattice points in ![]() that are in
that are in ![]() is 27 times the fraction of lattice points in
is 27 times the fraction of lattice points in ![]() that are in
that are in ![]() . What is the minimum possible value of the edge length of
. What is the minimum possible value of the edge length of ![]() plus the edge length of
plus the edge length of ![]() plus the edge length of
plus the edge length of ![]() ?
?
![]()
Solution
Let ![]() be the number of lattice points on the side length of square
be the number of lattice points on the side length of square ![]() ,
, ![]() be the number of lattice points on the side length of square
be the number of lattice points on the side length of square ![]() , and
, and ![]() be the number of lattice points on the side length of square
be the number of lattice points on the side length of square ![]() . Note that the actual lengths of the side lengths are the number of lattice points minus
. Note that the actual lengths of the side lengths are the number of lattice points minus ![]() , so we can work in terms of
, so we can work in terms of ![]() and subtract
and subtract ![]() to get the actual answer at the end. Furthermore, note that the number of lattice points inside a rectangular region is equal to the number of lattice points in its width times the number of lattice points along its length.
to get the actual answer at the end. Furthermore, note that the number of lattice points inside a rectangular region is equal to the number of lattice points in its width times the number of lattice points along its length.
Using this fact, the number of lattice points in ![]() is
is ![]() , the number of lattice points in
, the number of lattice points in ![]() is
is ![]() , and the number of lattice points in
, and the number of lattice points in ![]() is
is ![]() .
.
Now, by the first condition, we have ![]()
The second condition, the number of lattice points contained in ![]() is a fourth of the number of lattice points contained in
is a fourth of the number of lattice points contained in ![]() . The number of lattice points in
. The number of lattice points in ![]() is equal to the sum of the lattice points in their individually bounded regions, but the lattice points along the y-axis for the full length of square
is equal to the sum of the lattice points in their individually bounded regions, but the lattice points along the y-axis for the full length of square ![]() is shared by both of them, so we need to subtract that out.
is shared by both of them, so we need to subtract that out.
In all, this condition yields us ![]()
![]()
Note from ![]() that
that ![]() is a multiple of
is a multiple of ![]() . We can write
. We can write ![]() and substitute:
and substitute:
![]() .
Note that
.
Note that ![]() must be divisible by two for the product to be divisible by 4. Thus we make another substitution,
must be divisible by two for the product to be divisible by 4. Thus we make another substitution, ![]() :
:
![]()
Finally we look at the last condition; that the fraction of the lattice points inside ![]() that are inside
that are inside ![]() is
is ![]() times the fraction of lattice points inside
times the fraction of lattice points inside ![]() that are inside
that are inside ![]() .
.
Let ![]() be the number of lattice points along the bottom of the rectangle formed by
be the number of lattice points along the bottom of the rectangle formed by ![]() , and
, and ![]() be the number of lattice points along the bottom of the the rectangle formed by
be the number of lattice points along the bottom of the the rectangle formed by ![]() .
.
Therefore, the number of lattice points in ![]() is
is ![]() and the number of lattice points in
and the number of lattice points in ![]() is
is ![]() .
.
Thus by this condition, ![]()
Finally, notice that ![]() (subtracting overlap), and so we have
(subtracting overlap), and so we have ![]()
Now notice that by ![]() ,
, ![]() .
.
However, by ![]() ,
, ![]() . Therefore,
. Therefore, ![]()
Also, by ![]() , we know
, we know ![]() must be a perfect square since
must be a perfect square since ![]() is relatively prime to
is relatively prime to ![]() (Euclids algorithm) and the two must multiply to a perfect square. Hence we know two conditions on
(Euclids algorithm) and the two must multiply to a perfect square. Hence we know two conditions on ![]() , and we can now guess and check to find the smallest that satisfies both.
, and we can now guess and check to find the smallest that satisfies both.
We check ![]() first since its one less than a multiple of
first since its one less than a multiple of ![]() , but this does not work. Next, we have
, but this does not work. Next, we have ![]() which works because
which works because ![]() is a perfect square. Thus we have found the smallest
is a perfect square. Thus we have found the smallest ![]() , and therefore the smallest
, and therefore the smallest ![]() .
.
Now we just work backwards: ![]() and
and ![]() . Then
. Then ![]() . Finally, from
. Finally, from ![]() ,
, ![]() .
.
Finally, the sum of each square’s side lengths is ![]()
~KingRavi
Alternate Solution
Notice that each answer choice has a different residue mod ![]() . Therefore, we can just find the residue of
. Therefore, we can just find the residue of ![]() mod
mod ![]() and find the unique answer choice that fits, without actually finding
and find the unique answer choice that fits, without actually finding ![]() .
.
From Solution 1, we have ![]() from the second condition. From the third condition,
from the second condition. From the third condition, ![]() .
Substituting, we get
.
Substituting, we get ![]() . Therefore,
. Therefore, ![]() .
From the first condition, we have
.
From the first condition, we have ![]() , so
, so ![]() .
.
Therefore ![]() .
.
We want to find ![]() , so our answer will have a remainder of
, so our answer will have a remainder of ![]() when divided by
when divided by ![]() .
.
We divide ![]() by
by ![]() and find that the remainder is
and find that the remainder is ![]() . Therefore the answer that will give us a remainder of
. Therefore the answer that will give us a remainder of ![]() will be
will be ![]()
~KingRavi
See Also
| 2022 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.