Steiner line
Steiner line
Let ![]() be a triangle with orthocenter
be a triangle with orthocenter ![]() is a point on the circumcircle
is a point on the circumcircle ![]() of
of ![]() Then, the reflections of
Then, the reflections of ![]() in three edges
in three edges ![]() and point
and point ![]() lie on a line
lie on a line ![]() which is known as the Steiner line of point
which is known as the Steiner line of point ![]() with respect to
with respect to ![]()
Collings Clime
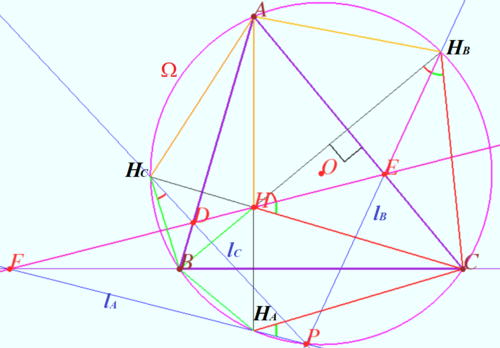
Let triangle ![]() be the triangle with the orthocenter
be the triangle with the orthocenter ![]() and circumcircle
and circumcircle ![]() Denote
Denote ![]() any line containing point
any line containing point ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in the edges
in the edges ![]() and
and ![]() respectively.
respectively.
Prove that lines ![]() and
and ![]() are concurrent and the point of concurrence lies on
are concurrent and the point of concurrence lies on ![]()
Proof
Let ![]() and
and ![]() be the crosspoints of
be the crosspoints of ![]() with
with ![]() and
and ![]() respectively.
respectively.
WLOG ![]() Let
Let ![]() and
and ![]() be the points symmetric to
be the points symmetric to ![]() with respect
with respect ![]() and
and ![]() respectively.
respectively.
Therefore ![]()
![]()
![]()
Let ![]() be the crosspoint of
be the crosspoint of ![]() and
and ![]() is cyclic
is cyclic ![]()
Similarly ![]() is cyclic
is cyclic ![]() the crosspoint of
the crosspoint of ![]() and
and ![]() is point
is point ![]()
Usually the point ![]() is called the anti-Steiner point of the
is called the anti-Steiner point of the ![]() with respect to
with respect to ![]()
vladimir.shelomovskii@gmail.com, vvsss