Complete Quadrilateral

Complete quadrilateral

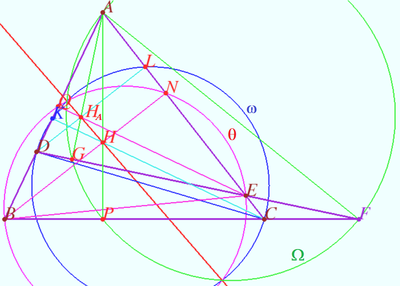
Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$ One can see some of the properties of this configuration and their proof using the following links.

Radical axis

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$

Let points $H,$ and $H_A$ be the orthocenters of $\triangle ABC$ and $\triangle ADE,$ respectively.

Let circles $\omega, \theta,$ and $\Omega$ be the circles with diameters $CD, BE,$ and $AF,$ respectively. Prove that Steiner line $HH_A$ is the radical axis of $\omega, \theta,$ and $\Omega.$

Proof

Let points $G, K, L, N, P,$ and $Q$ be the foots of perpendiculars $AH_A, CH, DH_A, BH, AH,$ and $EH_A,$ respectively.

Denote $Po(X)_{\omega}$ power of point $X$ with respect the circle $\omega.$ $\angle AGF = 90^\circ \implies G \in \Omega \implies Po(H_A)_{\Omega} = AH_A \cdot GH_A.$ $\angle CLD = 90^\circ \implies L \in \omega \implies Po(H_A)_{\omega} = DH_A \cdot LH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.$ $\angle EQB = 90^\circ \implies Q \in \theta \implies Po(H_A)_{\theta} = EH_A \cdot QH_A = AH_A \cdot GH_A = Po(H_A)_{\Omega}.$ $\angle APF = 90^\circ \implies P \in \Omega \implies Po(H)_{\Omega} = AH \cdot PH_A.$ $\angle BNE = 90^\circ \implies N \in \theta \implies Po(H)_{\theta} = BH \cdot NH = AH \cdot PH = Po(H)_{\Omega}.$ $\angle CKD = 90^\circ \implies K \in \theta \implies Po(H)_{\omega} = CH \cdot KH = AH \cdot PH = Po(H)_{\Omega}.$ Therefore power of points $H$ and $H_A$ with respect these three circles are the same, these points lies on the common radical axis of $\omega, \theta,$ and $\Omega \implies$ Steiner line $HH_A$ is the radical axis as desired.

Page

Toolbox

Search

Complete Quadrilateral

Complete quadrilateral

Radical axis