2022 AMC 12B Problems/Problem 10
Contents
Problem
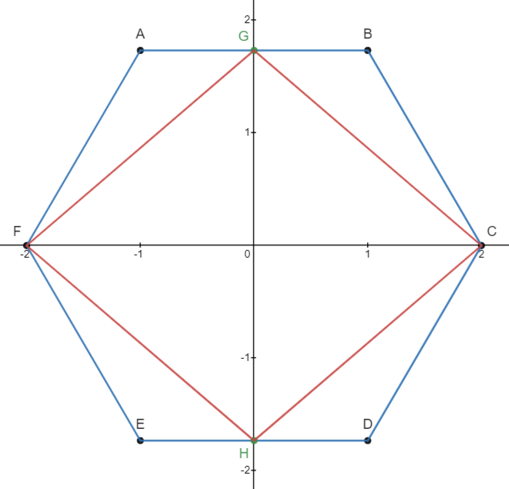
Regular hexagon ![]() has side length
has side length ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() . What is the perimeter of
. What is the perimeter of ![]() ?
?
![]()
Solution 1 (No trig)
Let the center of the hexagon be ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are all equilateral triangles with side length
are all equilateral triangles with side length ![]() . Thus,
. Thus, ![]() , and
, and ![]() . By symmetry,
. By symmetry, ![]() . Thus, by the Pythagorean theorem,
. Thus, by the Pythagorean theorem, ![]() . Because
. Because ![]() and
and ![]() ,
, ![]() . Thus, the solution to our problem is
. Thus, the solution to our problem is ![]()
~mathboy100
Solution 2
Consider triangle ![]() . Note that
. Note that ![]() ,
, ![]() , and
, and ![]() because it is an interior angle of a regular hexagon. (See note for details.)
because it is an interior angle of a regular hexagon. (See note for details.)
By the Law of Cosines, we have:

By SAS Congruence, triangles ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are congruent, and by CPCTC, quadrilateral
are congruent, and by CPCTC, quadrilateral ![]() is a rhombus. Therefore, the perimeter of
is a rhombus. Therefore, the perimeter of ![]() is
is ![]() .
.
Note: The sum of the interior angles of any polygon with ![]() sides is given by
sides is given by ![]() . Therefore, the sum of the interior angles of a hexagon is
. Therefore, the sum of the interior angles of a hexagon is ![]() , and each interior angle of a regular hexagon measures
, and each interior angle of a regular hexagon measures ![]() .
.
Solution 3
We use a coordinates approach. Letting the origin be the center of the hexagon, we can let ![]() Then,
Then, ![]() and
and ![]()
We use the distance formula four times to get ![]()
![]()
![]()
![]()
![]()
Thus, the perimeter of ![]() .
.
~sirswagger21
Note: the last part of this solution could have been simplified by noting that ![]()
Solution 4 (Fast)
Note that triangles ![]() and
and ![]() are all congruent, since they have side lengths of
are all congruent, since they have side lengths of ![]() and
and ![]() and an included angle of
and an included angle of ![]()
By the Law of Cosines, ![]()
Therefore, ![]()
-Benedict T (countmath1)
Video Solution 1
~Education, the Study of Everything
See Also
| 2022 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 9 |
Followed by Problem 11 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.