Feuerbach point

The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers and is named after Karl Wilhelm Feuerbach.

Sharygin’s prove

$1998, 24^{th}$ Russian math olympiad

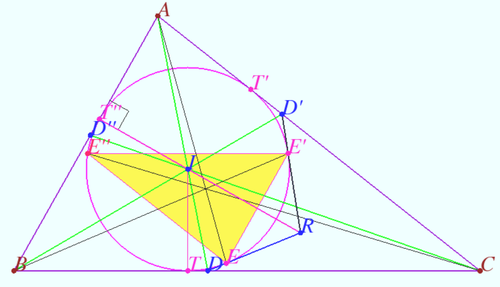
Claim 1

Let $D$ be the base of the bisector of angle A of scalene triangle $\triangle ABC.$

Let $DE$ be a tangent different from side $BC$ to the incircle of $\triangle ABC (E$ is the point of tangency). Similarly, we denote $D', E', D'',$ and $E''.$

Prove that $EE'||AB, \triangle ABC \sim \triangle EE'E'', AE, BE', CE''$ are concurrent.

Proof

Let $T, T',$ and $T''$ be the point of tangency of the incircle $\omega$ and $BC, AC,$ and $AB.$

Let $\angle A = 2 \alpha, \angle B = 2 \beta, \angle C = 2 \gamma, \alpha + \beta + \gamma = 90^\circ.$ WLOG, $\beta > \gamma.$ $\angle TIT'' = 180^\circ - 2 \beta, \angle ADB = 180^\circ - \alpha - 2 \beta,$ $\angle DIT = 90^\circ - \angle ADB = \alpha + 2 \beta - 90^\circ = \beta -\gamma, \angle EID = \angle TID \implies$ $\angle T''IE = \angle T''IT + 2 \angle TID = 180^\circ - 2 \beta + 2(\beta - \gamma) = 180^\circ - 2 \gamma.$ Similarly, $\angle T''IE' = 180^\circ – 2 \gamma \implies$ points $E$ and $E'$ are symmetric with respect $T''I \perp AB \implies AB || EE'.$

Similarly, $BC || E''E', AC || E''E \implies \triangle ABC \sim \triangle EE'E''.$

$AE, BE', CE''$ are concurrent at the homothetic center of $\triangle ABC$ and $\triangle EE'E''.$

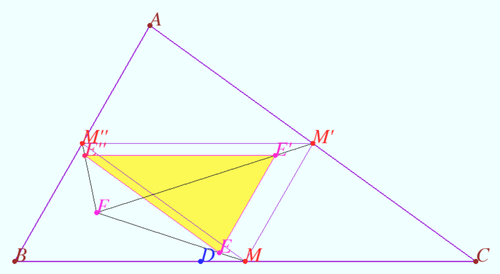
Claim 2

Let $M, M',$ and $M''$ be the midpoints $BC, AC,$ and $AB,$ respectively. Points $E, E',$ and $E''$ was defined at Claim 1.

Prove that $ME, M'E',$ and $M''E''$ are concurrent.

Proof

$\triangle ABC \sim \triangle MM'M'' \implies$ $\triangle MM'M'' \sim \triangle EE'E'' \implies$ $ME, M'E', M''E''$ are concurrent at the homothetic center of $\triangle MM'M''$ and $\triangle EE'E''.$

Page

Toolbox

Search

Feuerbach point

Sharygin’s prove