Cyclic quadrilateral

A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. While all triangles are cyclic, the same is not true of quadrilaterals. They have a number of interesting properties.

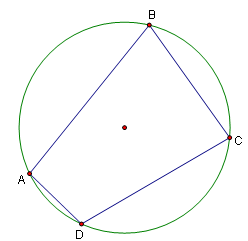
Properties

In a quadrilateral $ABCD$ :

$\angle A + \angle C = \angle B + \angle D = {180}^{o}$ This property is both sufficient and necessary, and is often used to show that a quadrilateral is cyclic.
$\angle ABD = \angle ACD$
$\angle BCA = \angle BDA$
$\angle BAC = \angle BDC$
$\angle CAD = \angle CBD$
All four perpendicular bisectors are concurrent. The converse is also true. This intersection is the circumcenter of the quadrilateral.
Any two opposite sites of the quadrilateral are antiparallel with respect TOTO SLOT to the other two opposite sites.
ef=ac+bd (e and f are the diagonals)