Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

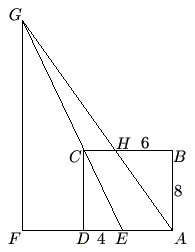
2003 AMC 10A Problems/Problem 22

Revision as of 13:26, 5 November 2006 by Xantos C. Guin (talk | contribs) (added pic)

Problem

In rectangle $ABCD$, we have $AB=8$, $BC=9$, $H$ is on $BC$ with $BH=6$, $E$ is on $AD$ with $DE=4$, line $EC$ intersects line $AH$ at $G$, and $F$ is on line $AD$ with $GF \perp AF$. Find the length of $GF$.

2003amc10a22.gif

$\mathrm{(A) \ } 16\qquad \mathrm{(B) \ } 20\qquad \mathrm{(C) \ } 24\qquad \mathrm{(D) \ } 28\qquad \mathrm{(E) \ } 30$

Solution

Since $ABCD$ is a rectangle, $CD=AB=8$.

Since $ABCD$ is a rectangle and $GF \perp AF$, $\angle GFE = \angle CDE = \angle ABC = 90^\circ$.

Since $ABCD$ is a rectangle, $AD || BC$.

So, $AH$ is a transversal, and $\angle GAF = \angle AHB$.

This is sufficient to prove that $GFE \approx CDE$ and $GFA \approx ABH$.

Using ratios:

$\frac{GF}{FE}=\frac{CD}{DE}$

$\frac{GF}{FD+4}=\frac{8}{4}=2$

$GF=2 \cdot (FD+4)=2 \cdot FD+8$

$\frac{GF}{FA}=\frac{AB}{BH}$

$\frac{GF}{FD+9}=\frac{8}{6}=\frac{4}{3}$

$GF=\frac{4}{3} \cdot (FD+9)=\frac{4}{3} \cdot FD+12$

Since $GF$ can't have 2 different lengths, both expressions for $GF$ must be equal.

$2 \cdot FD+8=\frac{4}{3} \cdot FD+12$

$\frac{2}{3} \cdot FD=4$

$FD=6$

$GF=2 \cdot FD+8=2\cdot6+8=20 \Rightarrow B$

See Also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_10A_Problems/Problem_22&oldid=11036"