2003 AMC 12A Problems/Problem 15
Problem
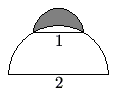
A semicircle of diameter ![]() sits at the top of a semicircle of diameter
sits at the top of a semicircle of diameter ![]() , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
![]()
Solution
The shaded area is equal to the area of the smaller semicircle minus the area of a sector of the larger circle plus the area of a triangle formed by two radii of the larger semicircle and the diameter of the smaller semicircle.
The area of the smaller semicircle is ![]() .
.
Since the radius of the larger semicircle is equal to the diameter of the smaller semicircle, the triangle is an equilateral triangle and the sector measures ![]() .
.
The area of the ![]() sector of the larger semicircle is
sector of the larger semicircle is ![]() .
.
The area of the triangle is ![]()
So the shaded area is ![]()