2021 Fall AMC 10B Problems/Problem 15
Contents
[hide]Problem
In square ![]() , points
, points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() , respectively. Segments
, respectively. Segments ![]() and
and ![]() intersect at right angles at
intersect at right angles at ![]() , with
, with ![]() and
and ![]() . What is the area of the square?
. What is the area of the square?
![[asy] size(170); defaultpen(linewidth(0.6)+fontsize(10)); real r = 3.5; pair A = origin, B = (5,0), C = (5,5), D = (0,5), P = (0,r), Q = (5-r,0), R = intersectionpoint(B--P,C--Q); draw(A--B--C--D--A^^B--P^^C--Q^^rightanglemark(P,R,C,7)); dot("$A$",A,S); dot("$B$",B,S); dot("$C$",C,N); dot("$D$",D,N); dot("$Q$",Q,S); dot("$P$",P,W); dot("$R$",R,1.3*S); label("$7$",(P+R)/2,NE); label("$6$",(R+B)/2,NE); [/asy]](http://latex.artofproblemsolving.com/9/3/0/9303b2a7f1e03de801c7915e1a61d7b755a6a43d.png)
![]()
Solution 1
Note that ![]() Then, it follows that
Then, it follows that ![]() Thus,
Thus, ![]() Define
Define ![]() to be the length of side
to be the length of side ![]() then
then ![]() Because
Because ![]() is the altitude of the triangle, we can use the property that
is the altitude of the triangle, we can use the property that ![]() Substituting the given lengths, we have
Substituting the given lengths, we have ![]() Solving, gives
Solving, gives ![]() and
and ![]() We eliminate the possibilty of
We eliminate the possibilty of ![]() because
because ![]() Thus, the side lengnth of the square, by Pythagorean Theorem, is
Thus, the side lengnth of the square, by Pythagorean Theorem, is ![]() Thus, the area of the sqaure is
Thus, the area of the sqaure is ![]() Thus, the answer is
Thus, the answer is ![]()
~NH14
Solution 2
Solution in Progress ~KingRavi
Solution 3
We have that ![]() Thus,
Thus, ![]() . Now, let the side length of the square be
. Now, let the side length of the square be ![]() Then, by the Pythagorean theorem,
Then, by the Pythagorean theorem, ![]() Plugging all of this information in, we get
Plugging all of this information in, we get ![]() Simplifying gives
Simplifying gives ![]() Squaring both sides gives
Squaring both sides gives ![]() We now set
We now set ![]() and get the equation
and get the equation ![]() From here, notice we want to solve for
From here, notice we want to solve for ![]() , as it is precisely
, as it is precisely ![]() or the area of the square. So we use the Quadratic formula, and though it may seem bashy, we hope for a nice cancellation of terms.
or the area of the square. So we use the Quadratic formula, and though it may seem bashy, we hope for a nice cancellation of terms. ![]() It seems scary, but factoring
It seems scary, but factoring ![]() from the square root gives us
from the square root gives us ![]() giving us the solutions
giving us the solutions ![]() We instantly see that
We instantly see that ![]() is way too small to be an area of this square (
is way too small to be an area of this square (![]() isn't even an answer choice, so you can skip this step if out of time) because then the side length would be
isn't even an answer choice, so you can skip this step if out of time) because then the side length would be ![]() and then, even the largest line you can draw inside the square (the diagonal) is
and then, even the largest line you can draw inside the square (the diagonal) is ![]() which is less than
which is less than ![]() (line
(line ![]() ) And thus,
) And thus, ![]() must be
must be ![]() , and our answer is
, and our answer is ![]()
![]()
~wamofan
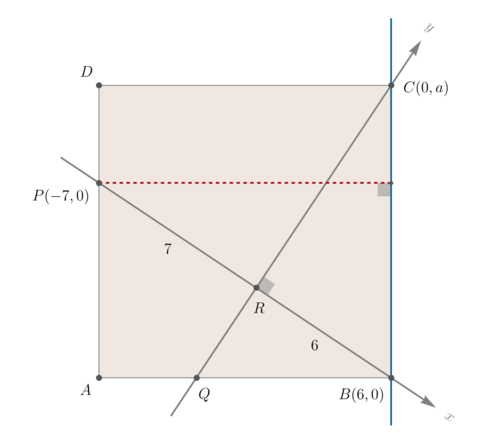
Solution 4 (Point-line distance formula)
Denote ![]() . Now tilt your head to the right and view
. Now tilt your head to the right and view ![]() and
and ![]() as the origin,
as the origin, ![]() -axis and
-axis and ![]() -axis, respectively. In particular, we have points
-axis, respectively. In particular, we have points ![]() . Note that side length of the square
. Note that side length of the square ![]() is
is ![]() . Also equation of line
. Also equation of line ![]() is
is
![\[\underbrace{\frac{x}{6} + \frac{y}{a} = 1}_{\text{intercepts form}} \quad \implies \quad ax + 6y - 6a = 0.\]](http://latex.artofproblemsolving.com/b/c/b/bcb9e70d5414a5c7f81392273aee5aa26b65f0dc.png) Because the distance from
Because the distance from ![]() to line
to line ![]() is also the side length
is also the side length ![]() , we can apply the point-line distance formula to get
, we can apply the point-line distance formula to get
![]() which reduces to
which reduces to ![]() . Since
. Since ![]() is positive, the last equations factors as
is positive, the last equations factors as
![]() . Now judging from the figure, we learn that
. Now judging from the figure, we learn that ![]() . So
. So ![]() .
Therefore, the area of the square
.
Therefore, the area of the square ![]() is
is ![]() . Choose
. Choose ![]() .
. ![]()
~VensL.
See Also
| 2021 Fall AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Problem 16 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.