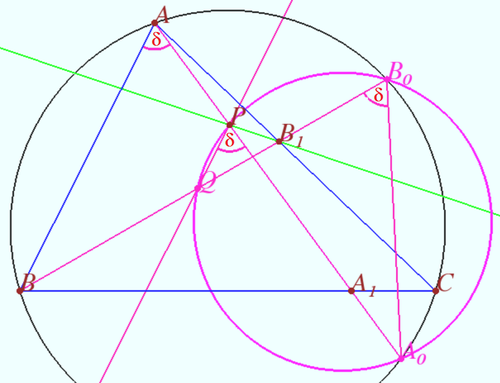
2019 IMO Problems/Problem 2

In triangle $ABC$ , point $A_1$ lies on side $BC$ and point $B_1$ lies on side $AC$ . Let $P$ and $Q$ be points on segments $AA_1$ and $BB_1$ , respectively, such that $PQ$ is parallel to $AB$ . Let $P_1$ be a point on line $PB_1$ , such that $B_1$ lies strictly between $P$ and $P_1$ , and $\angle PP_1C=\angle BAC$ . Similarly, let $Q_1$ be the point on line $QA_1$ , such that $A_1$ lies strictly between $Q$ and $Q_1$ , and $\angle CQ_1Q=\angle CBA$ .

Prove that points $P,Q,P_1$ , and $Q_1$ are concyclic.

Solution

The essence of the proof is to build a circle through the points $P, Q,$ and two additional points $A_0$ and $B_0,$ then we prove that the points $P_1$ and $Q_1$ lie on the same circle.

Let the circumcircle of $\triangle ABC$ be $\Omega$ . Let $A_0$ and $B_0$ be the points of intersection of $AP$ and $BQ$ with $\Omega$ . Let $\angle BAP = \delta.$

$PQ||AB \implies \angle QPA_0 = \delta.$

$\angle BAP = \angle BB_0A_0 = \delta$ since they intersept the arc $BA_0$ of the circle $\Omega$ .

$\angle QPA_0 = \angle QB_0A_0 \implies QPB_0A_0$ is cyclic (in circle $\omega.$ )

Page

Toolbox

Search

2019 IMO Problems/Problem 2

Solution