2019 IMO Problems/Problem 2
Problem
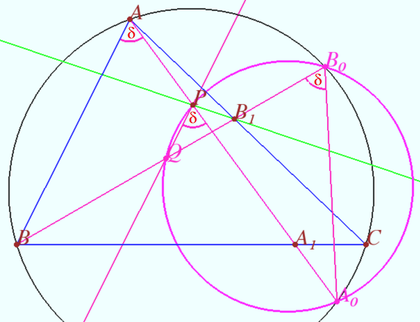
In triangle ![]() , point
, point ![]() lies on side
lies on side ![]() and point
and point ![]() lies on side
lies on side ![]() . Let
. Let ![]() and
and ![]() be points on segments
be points on segments ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() is parallel to
is parallel to ![]() . Let
. Let ![]() be a point on line
be a point on line ![]() , such that
, such that ![]() lies strictly between
lies strictly between ![]() and
and ![]() , and
, and ![]() . Similarly, let
. Similarly, let ![]() be the point on line
be the point on line ![]() , such that
, such that ![]() lies strictly between
lies strictly between ![]() and
and ![]() , and
, and ![]() .
.
Prove that points ![]() , and
, and ![]() are concyclic.
are concyclic.
Solution
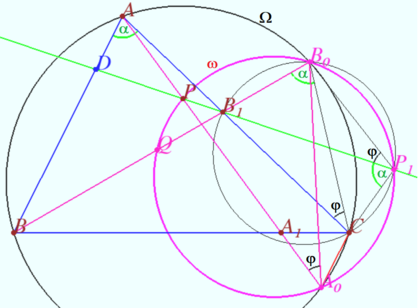
The essence of the proof is to build a circle through the points ![]() and two additional points
and two additional points ![]() and
and ![]() then we prove that the points
then we prove that the points ![]() and
and ![]() lie on the same circle.
lie on the same circle.
We assume that the intersection point of ![]() and
and ![]() lies on the segment
lies on the segment ![]() If it lies on segment
If it lies on segment ![]() then the proof is the same, but some angles will be replaced with additional ones up to
then the proof is the same, but some angles will be replaced with additional ones up to ![]() .
.
Let the circumcircle of ![]() be
be ![]() . Let
. Let ![]() and
and ![]() be the points of intersection of
be the points of intersection of ![]() and
and ![]() with
with ![]() . Let
. Let ![]()
![]()
![]() since they intersept the arc
since they intersept the arc ![]() of the circle
of the circle ![]() .
.
![]() is cyclic (in circle
is cyclic (in circle ![]() )
)
Let ![]()
![]() since they intersept the arc
since they intersept the arc ![]() of the circle
of the circle ![]() So
So ![]() is cyclic.
is cyclic.
![]() (they intersept the arc
(they intersept the arc ![]() of the circle
of the circle ![]()
![]()
![]() (since they intersept the arc
(since they intersept the arc ![]() of the circle
of the circle ![]()
Hence ![]() the point
the point ![]() lies on
lies on ![]()
Similarly, point ![]() lies on
lies on ![]()
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2019 IMO (Problems) • Resources | ||
| Preceded by Problem 1 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 3 |
| All IMO Problems and Solutions | ||