Miquel's point
Miquel and Steiner's quadrilateral theorem
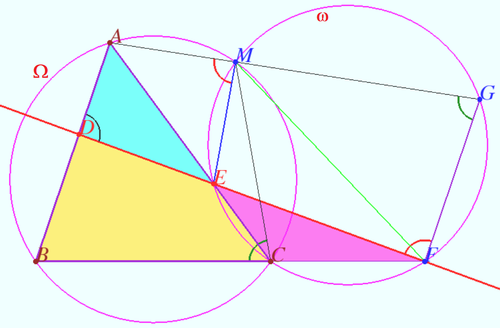
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]()
Prove that the circumcircles of all four triangles meet at a single point.
Proof
Let circumcircle of ![]() circle
circle ![]() cross the circumcircle of
cross the circumcircle of ![]() circle
circle ![]() at point
at point ![]()
Let ![]() cross
cross ![]() second time in the point
second time in the point ![]()
![]() is cyclic
is cyclic ![]()
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic and circumcircle of
is cyclic and circumcircle of ![]() contain the point
contain the point ![]()
Similarly circumcircle of ![]() contain the point
contain the point ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
Circle of circumcenters
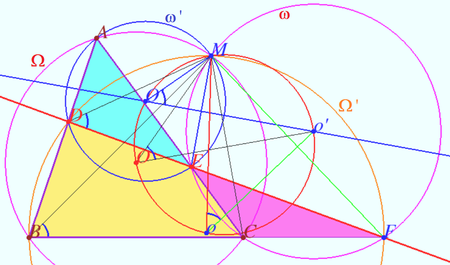
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]()
Prove that the circumcenters of all four triangles and point ![]() are concyclic.
are concyclic.
Proof
Let ![]() and
and ![]() be the circumcircles of
be the circumcircles of ![]() and
and ![]() respectively.
respectively.
In ![]()
In ![]()
![]() is the common chord of
is the common chord of ![]() and
and ![]()
![]()
Similarly, ![]() is the common chord of
is the common chord of ![]() and
and ![]()
Similarly, ![]() is the common chord of
is the common chord of ![]() and
and ![]()
![]() points
points ![]() and
and ![]() are concyclic as desired.
are concyclic as desired.
vladimir.shelomovskii@gmail.com, vvsss
Triangle of circumcenters
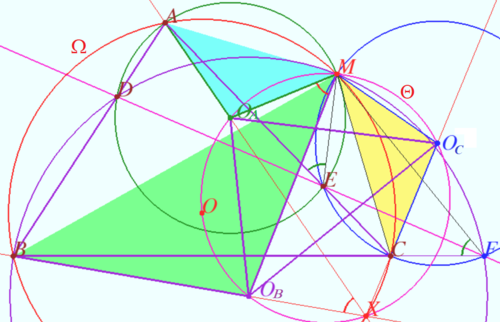
Let four lines made four triangles of a complete quadrilateral. In the diagram these are ![]() Let points
Let points ![]() and
and ![]() be the circumcenters of
be the circumcenters of ![]() and
and ![]() respectively.
Prove that
respectively.
Prove that ![]() and perspector of these triangles point
and perspector of these triangles point ![]() is the second (different from
is the second (different from ![]() ) point of intersection circumcircles of
) point of intersection circumcircles of ![]() and
and ![]() Proof
Quadrungle
Proof
Quadrungle ![]() is concyclic
is concyclic ![]()
![]()
![]() Spiral similarity sentered at point
Spiral similarity sentered at point ![]() with rotation angle
with rotation angle ![]() and the coefficient of homothety
and the coefficient of homothety ![]() mapping
mapping ![]() to
to ![]() ,
, ![]() to
to ![]() ,
, ![]() to
to ![]() \triangle O_AO_BO_C \sim \triangle ABC.$$ (Error compiling LaTeX. Unknown error_msg)\triangle AO_AM, \triangle BO_BM, \triangle CO_CM
\triangle O_AO_BO_C \sim \triangle ABC.$$ (Error compiling LaTeX. Unknown error_msg)\triangle AO_AM, \triangle BO_BM, \triangle CO_CM![]() M \implies
M \implies![]() \implies AO_A, BO_B, CO_C
\implies AO_A, BO_B, CO_C![]() X.
X.![]() \triangle AO_AM
\triangle AO_AM![]() \triangle BO_BM
\triangle BO_BM![]() O_AMO_B
O_AMO_B![]() O_AM
O_AM![]() O_BM
O_BM![]() AO_A
AO_A![]() BO_B
BO_B![]() \angle AXB \implies M O_AO_BX
\angle AXB \implies M O_AO_BX![]() implies M O_AO_BXO_C
implies M O_AO_BXO_C![]() \implies \angle O_AXO_B = \angle O_AO_CO_B = \angle ACB \implies ABCX$ is cyclic as desired.
\implies \angle O_AXO_B = \angle O_AO_CO_B = \angle ACB \implies ABCX$ is cyclic as desired.
vladimir.shelomovskii@gmail.com, vvsss