Spieker center
The Spieker center is defined as the center of mass of the perimeter of the triangle. The Spieker center of a ![]() is the center of gravity of a homogeneous wire frame in the shape of
is the center of gravity of a homogeneous wire frame in the shape of ![]() The Spieker center is a triangle center and it is listed as the point
The Spieker center is a triangle center and it is listed as the point ![]()
Contents
Incenter of medial triangle
Prove that the Spieker center of triangle ![]() is the incenter of the medial triangle
is the incenter of the medial triangle ![]() of a
of a ![]()
Proof
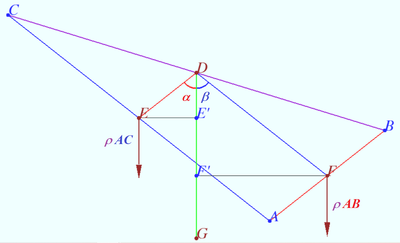
Let's hang up the ![]() in the middle of side
in the middle of side ![]() Side
Side ![]() is balanced.
is balanced.
Let's replace side ![]() with point
with point ![]() (the center of mass of
(the center of mass of ![]() the midpoint
the midpoint ![]() Denote
Denote ![]() the linear density of a homogeneous wire frame.
the linear density of a homogeneous wire frame.
The mass of point ![]() is equal to
is equal to ![]() the shoulder of the gravity force is
the shoulder of the gravity force is ![]()
The moment of this force is ![]()
Similarly the moment gravity force acting on AB is ![]()
Therefore, equilibrium condition is ![]() and the center of gravity of a homogeneous wire frame
and the center of gravity of a homogeneous wire frame ![]() lies on each bisector of
lies on each bisector of ![]()
This point is the incenter of the medial triangle ![]()
vladimir.shelomovskii@gmail.com, vvsss
Intersection of three cleavers
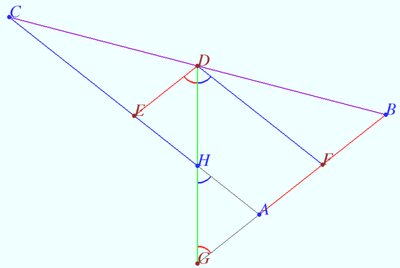
Prove that the Spieker center is located at the intersection of the three cleavers of triangle. A cleaver of a triangle is a line segment that bisects the perimeter of the triangle and has one endpoint at the midpoint of one of the three sides.
Proof
We use notation of previous proof. ![]() is the segment contains the Spieker center,
is the segment contains the Spieker center, ![]() WLOG,
WLOG, ![]()
![]() Similarly,
Similarly, ![]()
So ![]() is cleaver.
is cleaver.
Therefore, the three cleavers meet at the Spieker center.
vladimir.shelomovskii@gmail.com, vvsss
Radical center of excircles
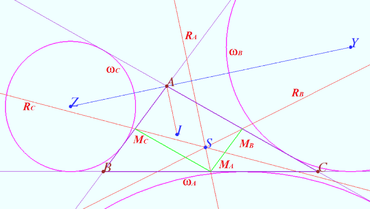
Prove that the Spieker center of triangle is the radical center of the three excircles.
Proof
Let ![]() be given,
be given,![]() be the midpoints of
be the midpoints of ![]() respectively.
respectively.
Let ![]() be A-excircle, B-excircle, C-excircle centered at
be A-excircle, B-excircle, C-excircle centered at ![]() respectively.
respectively.
Let ![]() be the incenter of
be the incenter of ![]() Let
Let ![]() be the radical axis of
be the radical axis of ![]() and
and ![]() be the radical axis of
be the radical axis of ![]() and
and ![]() be the radical axis of
be the radical axis of ![]() and
and ![]() respectively.
respectively.
It is known that the distances from ![]() to the tangent points of
to the tangent points of ![]() is equal to the distances from
is equal to the distances from ![]() to the tangent points of
to the tangent points of ![]() therefore
therefore ![]() lies on the radical axis
lies on the radical axis ![]() of
of ![]() and
and ![]() Similarly,
Similarly, ![]()
![]() is cleaver. Similarly,
is cleaver. Similarly, ![]() and
and ![]() are cleavers.
are cleavers.
Therefore the radical center of the three excircles coinside with the intersection of the three cleavers of triangle.
vladimir.shelomovskii@gmail.com, vvsss
Nagel line
Let points ![]() be the incenter, the centroid and the Spieker center of triangle
be the incenter, the centroid and the Spieker center of triangle ![]() respectively. Prove that points
respectively. Prove that points ![]() are collinear,
are collinear, ![]() and the barycentric coordinates of S are
and the barycentric coordinates of S are ![]()
The Nagel line is the line on which points ![]() and Nagel point
and Nagel point ![]() lie.
lie.
Proof
Let ![]() be the midpoints of
be the midpoints of ![]() respectively.
Bisector
respectively.
Bisector ![]() is parallel to cleaver
is parallel to cleaver ![]()
![]() Centroid
Centroid ![]() divide the median
divide the median ![]() such that
such that ![]()
![]() and points
and points ![]() are collinear.
are collinear.
The barycentric coordinates of ![]() are
are ![]() The barycentric coordinates of
The barycentric coordinates of ![]() are
are ![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
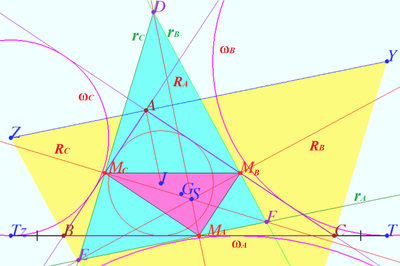
Shatunov triangle
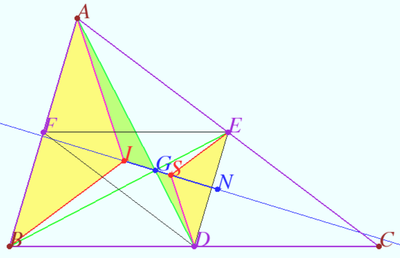
Let ![]() be given. Let
be given. Let ![]() be incircle, A-excircle, B-excircle, C-excircle centered at points
be incircle, A-excircle, B-excircle, C-excircle centered at points ![]() respectively.
respectively.
Let ![]() be the radical axes of the inscribed circle and one of the excircles of
be the radical axes of the inscribed circle and one of the excircles of ![]()
The triangle ![]() whose sides are
whose sides are ![]() we name the Shatunov triangle. Accordingly, the vertices of the Shatunov triangle are the radical centers of a pair of excircles and an inscribed circle.
we name the Shatunov triangle. Accordingly, the vertices of the Shatunov triangle are the radical centers of a pair of excircles and an inscribed circle.
Prove:
a) the heights of the Shatunov triangle lie on the bisectors of the medial triangle. The orthocenter of the Shatunov triangle is the Steiner point of ![]()
b) The Shatunov triangle is homothetic to the anticomplementary triangle of ![]() with respect to the centroid
with respect to the centroid ![]() with coefficient
with coefficient ![]()
Proof
a) Let ![]() be the midpoints of
be the midpoints of ![]() respectively.
respectively.
The distances from ![]() to the tangent points of
to the tangent points of ![]() and
and ![]() are the same, so
are the same, so ![]() Similarly
Similarly ![]()
Let ![]() and
and ![]() be the points of tangency of
be the points of tangency of ![]() and
and ![]() and
and ![]() respectively.
respectively.
It is clear that ![]() lies on the radical axis
lies on the radical axis ![]()
Similarly, ![]() lies on the radical axis
lies on the radical axis ![]() lies on the radical axis
lies on the radical axis ![]()
![]() D is the radical center of
D is the radical center of ![]()
![]() Similarly
Similarly ![]()
Therefore ![]() are the heights of
are the heights of ![]() is the orthocenter of
is the orthocenter of ![]()
![]() is the medial triangle of
is the medial triangle of ![]() is the bisector of
is the bisector of ![]() is the Steiner point of
is the Steiner point of ![]()
b) ![]()
![]() is the orthocenter of
is the orthocenter of ![]() is the orthocenter of
is the orthocenter of ![]()
Points ![]() and
and ![]() where
where ![]() is the centroid
is the centroid ![]() are collinear, sides of is the
are collinear, sides of is the ![]() are parallel to the respective sides of
are parallel to the respective sides of ![]() is homothetic to the
is homothetic to the ![]() with respect to
with respect to ![]()
![]() the coefficient of homothety is
the coefficient of homothety is ![]()
vladimir.shelomovskii@gmail.com, vvsss