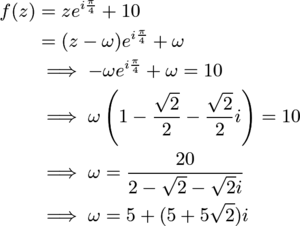2008 AIME II Problems/Problem 9
Problem
A particle is located on the coordinate plane at ![]() . Define a move for the particle as a counterclockwise rotation of
. Define a move for the particle as a counterclockwise rotation of ![]() radians about the origin followed by a translation of
radians about the origin followed by a translation of ![]() units in the positive
units in the positive ![]() -direction. Given that the particle's position after
-direction. Given that the particle's position after ![]() moves is
moves is ![]() , find the greatest integer less than or equal to
, find the greatest integer less than or equal to ![]() .
.
Contents
[hide]Solutions
Solution 1
Let ![]() be the position of the particle on the
be the position of the particle on the ![]() -plane,
-plane, ![]() be the length
be the length ![]() where
where ![]() is the origin, and
is the origin, and ![]() be the inclination of OP to the x-axis. If
be the inclination of OP to the x-axis. If ![]() is the position of the particle after a move from
is the position of the particle after a move from ![]() , then we have two equations for
, then we have two equations for ![]() and
and ![]() :
:
![]()
![]() Let
Let ![]() be the position of the particle after the nth move, where
be the position of the particle after the nth move, where ![]() and
and ![]() . Then
. Then ![]() ,
, ![]() . This implies
. This implies
![]() ,
, ![]() .
Substituting
.
Substituting ![]() and
and ![]() , we have
, we have ![]() and
and ![]() again for the first time. Thus,
again for the first time. Thus, ![]() and
and ![]() . Hence, the final answer is
. Hence, the final answer is
If you're curious, the points do eventually form an octagon and repeat. Seems counterintuitive, but believe it or not, it happens.
https://www.desmos.com/calculator/febtiheosz
Solution 2
Let the particle's position be represented by a complex number. Recall that multiplying a number by cis![]() rotates the object in the complex plane by
rotates the object in the complex plane by ![]() counterclockwise. In this case, we use
counterclockwise. In this case, we use ![]() . Therefore, applying the rotation and shifting the coordinates by 10 in the positive x direction in the complex plane results to
. Therefore, applying the rotation and shifting the coordinates by 10 in the positive x direction in the complex plane results to
where a is cis![]() . By De-Moivre's theorem,
. By De-Moivre's theorem, ![]() =cis
=cis![]() .
Therefore,
.
Therefore,
Furthermore, ![]() . Thus, the final answer is
. Thus, the final answer is
Solution 3
As before, consider ![]() as a complex number. Consider the transformation
as a complex number. Consider the transformation ![]() . This is a clockwise rotation of
. This is a clockwise rotation of ![]() by
by ![]() radians about the points
radians about the points ![]() . Let
. Let ![]() denote one move of
denote one move of ![]() . Then
. Then
Therefore, ![]() rotates along a circle with center
rotates along a circle with center ![]() . Since
. Since ![]() ,
, ![]() , as desired (the final algebra bash isn't bad).
, as desired (the final algebra bash isn't bad).
Solution 4
Let ![]() . We assume that the rotation matrix
. We assume that the rotation matrix ![]() here. Then we have
here. Then we have
This simplifies to
Since ![]() , so we have
, so we have ![]() , giving
, giving ![]() . The answer is yet
. The answer is yet ![]() .
.
See also
| 2008 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()