1992 OIM Problems/Problem 3

Problem

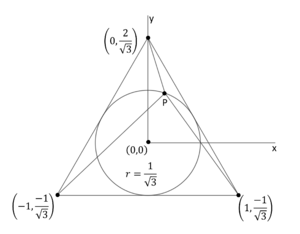
In an equilateral triangle $ABC$ whose side has length 2, the circle $G$ is inscribed.

a. Show that for every point $P$ of $G$ , the sum of the squares of its distances to the vertices $A$ , $B$ and $C$ is 5.

b. Show that for every point $P$ in $G$ it is possible to construct a triangle whose sides have the lengths of the segments $AP$ , $BP$ and $CP$ , and that its area is:

$\frac{\sqrt{3}}{4}$

~translated into English by Tomas Diaz. ~orders@tomasdiaz.com

Solution

Note. I actually competed at this event in Venezuela when I was in High School representing Puerto Rico. I got full points for part a and partial points for part b. I don't remember what I did. I will try to write a solution for this one later.

This problem needs a solution. If you have a solution for it, please help us out by adding it.

Page

Toolbox

Search

1992 OIM Problems/Problem 3

Problem

Solution

See also