Projective geometry (simplest cases)

Projective geometry contains a number of intuitively obvious statements that can be effectively used to solve some Olympiad mathematical problems.

Useful simplified information

Let two planes $\Pi$ and $\Pi'$ and a point $O$ not lying in them be defined in space. To each point $A$ of plane $\Pi$ we assign the point $A'$ of plane $\Pi'$ at which the line $AO$ intersects this plane. We want to find a one-to-one mapping of plane $\Pi$ onto plane $\Pi'$ using such a projection.

We are faced with the following problem. Let us construct a plane containing a point $O$ and parallel to the plane $\Pi'.$ Let us denote the line along which it intersects the plane $\Pi$ as $\ell.$ No point of the line $\ell$ has an image in the plane $\Pi'.$ Such new points are called points at infinity.

To solve it, we turn the ordinary Euclidean plane into a projective plane. We consider that the set of all points at infinity of each plane forms a line. This line is called the line at infinity. The plane supplemented by such line is called the projective plane, and the line for which the central projection is not defined is called (in Russian tradition) the exceptional line of the transformation. We define the central projection as follows.

Let us define two projective planes $\Pi$ and $\Pi'$ and a point $O.$

For each point $A$ of plane $\Pi$ we assign either:

- the point $A'$ of plane $\Pi'$ at which line $AO$ intersects $\Pi',$

- or a point at infinity if line $AO$ does not intersect plane $\Pi'.$

We define the inverse transformation similarly.

A mapping of a plane onto a plane is called a projective transformation if it is a composition of central projections and affine transformations.

Properties of a projective transformation

1. A projective transformation is a one-to-one mapping of a set of points of a projective plane, and is also a one-to-one mapping of a set of lines.

2. The inverse of a projective transformation is projective transformation. The composition of projective transformations is a projective transformation.

3. Let two quadruples of points $A, B, C, D$ and $A', B', C', D'$ be given. In each quadruple no three points lie on the same line: Then there exists a unique projective transformation that maps $A$ to $A',$ $B$ to $B', C$ to $C', D$ to $D'.$

4. There is a central projection that maps any quadrilateral to a square. A square can be obtained as a central projection of any quadrilateral.

5. There is a central projection that maps a circle to a circle, and a chosen interior point of the first circle to the center of the second circle. This central projection maps the polar of the chosen point to the line at infinity.

6. The relationships of segments belonging to lines parallel to the exceptional line are the same for images and preimages.

7. The double (anharmonic) ratio for given four points $A, B, C, D$ on a line (or on a circle) is a number $(A,B;C,D) = \frac {AC\cdot BD}{BC\cdot AD}.$

It is the only projective invariant of a quadruple of collinear points.

Projection of a circle into a circle

Let a circle $\omega$ with diameter $PQ$ and a point $A$ on this diameter $(2AP < PQ)$ be given.

Find the prospector of the central projection that maps the circle $\omega$ into the circle $\omega'$ and the point $A$ into point $O'$ - the center of $\omega'.$

Solution

Let $S$ be the center of transformation (perspector) which is located on the perpendicular through the point $P$ to the plane containing $\omega.$ Let $P = \omega \cap \omega', PQ'$ be the diameter of $\omega', PO' = O'Q'$ and plane $\omega'$ is perpendicular to $SQ.$

Spheres with diameter $PQ$ and with diameter $PS$ contain a point $Q'$ , so they intersect along a circle $\omega'.$

Therefore the circle $\omega$ is a stereographic projection of the circle $\omega'$ from the point $S.$

That is, if the point $M$ lies on $\omega$ , there is a point $M'$ on the circle $\omega'$ along which the line $SM$ intersects $\omega'.$

It means that $\omega$ is projected into $\omega'$ under central projection from the point $S.$

$PQ \perp SQ, PQ' \perp SQ \implies PQ'$ is antiparallel $PQ$ in $\triangle SPQ.$

$PO' = O'Q' \implies SA$ is the symmedian. $\frac {AQ}{AP} = \frac {SQ^2}{SP^2} \implies \frac {QP - AP}{AP} = \frac {SP^2 + PQ^2}{SP^2} \implies SP = \frac {QP}{\sqrt{\frac {QP}{AP}-2}}.$

Corollary

Let $Q'P || SA_0 \implies SA_0 \perp SQ \implies SP^2 = QP \cdot PA_0 = \frac {QP^2}{\frac {QP}{AP} - 2} \implies$ $PA_0 = \frac {AP \cdot OP}{OP – AP} \implies OA \cdot OA_0 = OP^2 .$ The inverse of a point $A$ with respect to a reference circle $\omega$ is $A_0.$

The line throught $A_0$ in plane of circle $\omega$ perpendicular to $PQ$ is polar of point $A.$

The central projection of this line to the plane of circle $\omega'$ from point $S$ is the line at infinity.

vladimir.shelomovskii@gmail.com, vvsss

Butterfly theorem

Let $M$ be the midpoint of a chord $PQ$ of a circle $\omega,$ through which two other chords $AB$ and $CD$ are drawn; $AC$ and $BD$ intersect chord $PQ$ at $X$ and $Y$ correspondingly.

Prove that $M$ is the midpoint of $XY.$

Proof

Let point $O$ be the center of $\omega, OM \perp PQ.$

We make the central projection that maps the circle $\omega$ into the circle $\omega'$ and the point $M$ into the center of $\omega'.$

Let's designate the images points with the same letters as the preimages points.

Chords $AB$ and $CD$ maps into diameters, so $ACBD$ maps into rectangle and in this plane $M$ is the midpoint of $XY.$

The exceptional line of the transformation is perpendicular to $OM,$ so parallel to $PQ.$

The relationships of segments belonging to lines parallel to the exceptional line are the same for images and preimages. We're done! $\blacksquare$ .

vladimir.shelomovskii@gmail.com, vvsss

Sharygin’s Butterfly theorem

Let a circle $\Omega$ and a chord $PQ$ be given. Points $E$ and $F$ lyes on $PQ$ such that $PE = QF (2PE > PQ).$ Chords $AB$ and $CD$ are drawn through points $E$ and $F,$ respectively such that quadrilateral $ACBD$ is convex.

Lines $AC$ and $BD$ intersect the chord $PQ$ at points $X$ and $Y.$

Prove that $PX=QY.$

Proof

Let us perform a projective transformation that maps the midpoint of the chord $PQ$ to the center of the circle $\Omega$ . The image $PQ$ will become the diameter, the equality $PE = QF$ will be preserved.

Let $B'$ and $D'$ be the points symmetrical to the points $B$ and $D$ with respect to line $\ell,$ the bisector $PQ.$

Denote $\omega = \odot AXE, K = \omega \cap \Omega.$ (Sharygin’s idea.)

$AKXE$ is cyclic $\implies \angle KXE = 180^\circ - \angle KAE.$

$AKB'B$ is cyclic $\implies \angle KB'B = 180^\circ - \angle KAB = \angle KXE.$

$PQ||B'B \implies$ points $K, X,$ and $B'$ are collinear.

Similarly points $K, E,$ and $D'$ are collinear.

We use the symmetry lines $DF$ and $D'E$ with respect $\ell$ and get in series

$-$ symmetry $K$ and $C$ with respect $\ell,$

$-$ symmetry $KB'$ and CB with respect $\ell,$

$-$ symmetry $X$ and $Y$ with respect $\ell.$

vladimir.shelomovskii@gmail.com, vvsss

Semi-inscribed circle

Let triangle $\triangle ABC$ and circle $\omega$ centered at point $O$ and touches sides $AB$ and $AC$ at points $E$ and $F$ be given.

Point $D$ is located on chord $EF$ so that $DO \perp BC.$

Prove that points $A, D,$ and $M$ (the midpoint $BC)$ are collinear.

Proof

Denote $K = AO \cap EF, r = OE, A' -$ point on line $DO$ such that $AA' || BC.$

$\frac {OK}{OD} = \frac{OA'}{AO}, \frac {OK}{OE} = \frac{OE}{AO} \implies OD \cdot OA' = r^2 .$

Therefore line $AA'$ is the polar of $D.$

Let us perform a projective transformation that maps point $D$ to the center of $\omega.$

Image $A$ is the point at infinity, so images $AB, AD,$ and $AC$ are parallel.

Image $EF$ is diameter, so image $D$ is midpoint of image $EF$ and image $M$ is midpoint of image $BC.$

$BC || AA',$ so image $BC$ is parallel to the line at infinity and the ratio $\frac {BM}{MC}$ is the same as ratio of images.

vladimir.shelomovskii@gmail.com, vvsss

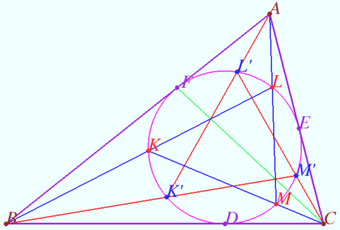
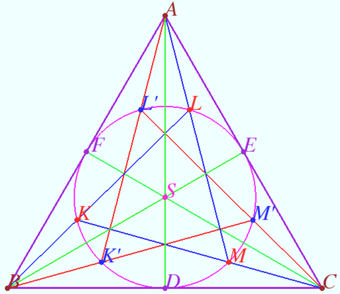
Fixed point

Let triangle $\triangle ABC$ and circle $\omega$ centered at point $O$ and touches sides $AB$ and $AC$ at points $E$ and $F$ be given.

The points $P$ and $Q$ on the side $BC$ are such that $BP = QC.$

The cross points of segments $AP$ and $AQ$ with $\omega$ form a convex quadrilateral $KK'LL'.$

Point $D$ lies at $FE$ and satisfies the condition $DO \perp BC.$

Prove that $D \in KL.$

Proof

Let us perform a projective transformation that maps point $D$ to the center of $\omega.$

Image $A$ is the point at infinity, so images $AB, AP, AQ,$ and $AC$ are parallel. The plane of images is shown, notation is the same as for preimages.

Image $EF$ is diameter $\omega,$ image $BC$ is parallel to the line at infinity, so in image plane $\frac {BP}{BC} = \frac {QC}{BC}, BP = QC.$

Denote $M = EF \cap PK, N = EF \cap QL.$ $\frac {EM}{BP} = \frac {NF}{QC} \implies EM = NF \implies MD = ND,$ $KM \perp EF, LN \perp EF \implies$ $KK'LL'$ is rectangle, so $D \in KL. \blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Set of lines

Let points $D$ at the line $BC, E$ at the line $AC, F$ at the line $AB$ be given.

Denote circle $\omega = \odot DEF, D' = \omega \cap BC \ne D,$ $E' = \omega \cap AC \ne E, F' = \omega \cap AB \ne F,$ $A' = D'E \cap DF', B' = EA' \cap FE', C' = FE' \cap DF'.$

Prove that lines $AA', BB',$ and $CC'$ are concurrent.

Proof

According the Pascal theorem in case shown in diagram points $DD' \cap E'F, FF' \cap D'E,$ and $EE' \cap DF'$ are collinear at Pascal line.

Note that lines $DD' = BC, EE' = AC, FF' = AB.$

Let point $X$ be the pole of Pascal line.

Let us perform a projective transformation that maps point $X$ to the center of $\omega.$

Then image of $AB$ is parallel to image of $D'E,$ image of $BC$ is parallel to image of $E'F,$ , image of $AC$ is parallel to image of $DF'.$

As shown in ( Set of parallel lines) images of lines $AA', BB',$ and $CC'$ are concurrent.

Therefore lines $AA', BB',$ and $CC'$ are concurrent.

vladimir.shelomovskii@gmail.com, vvsss

Set of lines in circle and triangle

Let points $D$ at the line $BC, E$ at the line $AC, F$ at the line $AB$ be given. Denote circle $\omega = \odot DEF, D' = \omega \cap BC \ne D,$ $E' = \omega \cap AC \ne E, F' = \omega \cap AB \ne F,$ $K = AD \cap CF', K' = CF \cap AD', L = BE \cap AD',$ $L' = AD \cap BE', N = BE \cap CF', N' = BE' \cap CF.$

Prove that lines $KK', LL',$ and $NN'$ are concurrent.

Proof

Let us consider the inscribed hexagon $DEFE'F'D',$ shown in diagram. According the Pascal theorem points $DD' \cap E'F, FF' \cap DE,$ and $EE' \cap D'F'$ are collinear at Pascal line. Note that lines $DD' = BC, EE' = AC, FF' = AB.$

The Pascal line has no common point with $\omega,$ so the pole of this line is the inner point of the circle.

Let us perform a projective transformation that maps this pole to the center of $\omega.$

Image of $DD' \cap E'F$ is the point at infinity, so image $BC$ is parallel to image $E'F.$ Similarly, images $AB$ and $AC$ are parallel to images $DE$ and $D'F'.$

As shown in ( Set of lines in triangle) images of lines $KK', LL',$ and $NN'$ are concurrent. Therefore lines $KK', LL',$ and $NN'$ are concurrent.

vladimir.shelomovskii@gmail.com, vvsss

Projection of any triangle into regular one

Find a projective transformation that maps the given triangle into a regular one, and its inscribed circle into a circle.

Solution

Any point of tangency of the circle and line and any crosspoint of the lines are invariants of any projective transformation. Therefore, the Gergonne point of preimage maps into Gergonne point of image.

We make transformation which maps the Gergonne point of given triangle into the center if the incircle. According with Lemma, given triangle maps into regular one.

Lemma

Let the Gergonne point of $\triangle ABC$ coincide with the incenter of this triangle. Prove that $\triangle ABC$ is regular.

Proof

The inradius connect the incenter and point of tangency, bisector connect vertex and incenter, Gergonne point belong the line connect vertex and point of tangency, so these objects lie at the same line.

The radius is perpendicular to the side at the points of tangency, which means that the bisector coincide with the altitude of the triangle. The axial symmetry with respect to bisector maps one side of triangle to another, the base side is perpendicular to the bisector so symmetric sides are equal. Applying symmetry with respect to another bisector, we find that all three sides are equal and the triangle is regular.

vladimir.shelomovskii@gmail.com, vvsss

Some properties of an equilateral triangle

Let an equilateral triangle $\triangle ABC, AB = 2a$ be given. Denote $\omega$ the incircle of $\triangle ABC, D = BC \cap \omega,$

$E = AC \cap \omega, F = AB \cap \omega, O = AD \cap BE, S = ML' \cap AD.$

Points $K, L, M, K', L', M'$ are located on $\omega$ so that ordered triplets of points $(A,L,M), (A,L',K'), (B,K,L), (B,K',M'), (C,M,K), (C,K',M')$ are collinear.

Find $LM, AL, \angle OAL, LL', K'M, AS,$ and $\frac{LL' \cdot K'M' \cdot KM}{K'M \cdot L'M' \cdot KL}.$

Prove that quadrilateral $LMOS$ is cyclic, $\odot LMO$ is tangent to $KC$ and symmetric to $\omega$ with respect $AM.$

Proof

1. The circumradius $R = AO$ is twice the inradius $OD = r.$ From considerations of symmetry we conclude that $\triangle KLM$ is regular, so $\triangle KLM \sim \triangle ABC \implies \frac {AO}{OD} = \frac {AB}{LM} = 2 \implies LM = a.$ $2.\hspace{10mm} AE^2 = AL \cdot AM = AL \cdot (AL + LM) \implies$

$AL = \frac {LM}{\varphi} = \frac {a}{\varphi},$ where $\varphi$ is the golden ratio: $\varphi = \frac{\sqrt{5}+1} {2}.$

3. Let $\theta$ be the angle of rotation of the spiral similarity that maps $\triangle ABC$ into $\triangle KLM \implies \theta = \angle CAL = \angle AOL.$ $\angle ALO = 180^\circ - \angle OAL - \angle AOL = 180^\circ - \angle OAL - \angle CAL = 180^\circ - \angle OAC = 150^\circ .$ By applying the Law of Sines on $\triangle ALO,$ we get $\sin \angle OAL = \frac {OL}{OA} \sin \angle ALO = \frac {\sin 150^\circ}{2} = \frac {1}{4} \implies \angle OAL = \arcsin \frac {1}{4} .$ $4.\hspace{10mm} LL' = 2 AL \sin \angle OAL = \frac {AL}{2} = \frac {a}{2 \varphi}, K'M = \frac {AM}{2} = \frac {a \varphi}{2} \implies K'M - LL' = \frac {a}{2}.$

$5.\hspace{10mm} AS$ is A-bisector of $\triangle AL'M \implies$ $AS = \frac {2 \cos \angle OAL} {AL'^{-1}+ AM^{-1}} = \frac {a \sqrt{3}}{2} = \frac{AD}{2}.$ So $S$ is the midpoint $AD.$ Similarly, $S \in K'L.$

$6.\hspace{10mm} \frac{LL' \cdot K'M' \cdot KM}{K'M \cdot L'M' \cdot KL} = \frac{LL'}{K'M} = \frac{1}{\varphi^2}.$

$7.\hspace{10mm}\angle LOM = 120^\circ \implies \overset{\Large\frown} {LM} = 120^\circ = \overset{\Large\frown} {L'K'} \implies \angle LSM = 120^\circ.$ $\angle MLO = 30^\circ = \angle KMO, OL = OM = r.$ Corollary

Lines $EF, K'L, L'M,$ and $AD$ are concurrent.

vladimir.shelomovskii@gmail.com, vvsss

Two generated triangles

Let triangle $\triangle ABC$ be given. Denote $\omega$ the incircle of $\triangle ABC, F = AB \cap \omega$ .

Points $K, L, M, K', L', M'$ are located on $\omega$ so that ordered triplets of points $(A,L,M), (A,L',K'), (B,K,L), (B,K',M'), (C,M,K), (C,K',M')$ are collinear.

Prove that lines $L'K', KL,$ and $CF$ are concurrent.

Proof

We make projective transformation which maps the incircle into circle and the Gergonne point $S$ of given triangle $\triangle ABC$ into the center of the incircle.

The image of $\triangle ABC$ is a regular triangle in which image of line $CF$ is the axis of symmetry.

The images of the points $A$ and $B$ are symmetric with respect to the image of the line $CF.$

The image of $\omega$ is symmetric with respect to the image of the line $CF.$

The image of the line $CK$ is symmetric to image of line $CL'$ with respect to image of the line $CF,$ so images of points $K$ and $L' (M$ and $M')$ are symmetric with respect to the image of the line $CF.$

Similarly, images of points $L$ and $K'$ are symmetric with respect to the image of the line $CF.$ So point $KL \cap L'K'$ lies at the line of the symmetry, i.e. the image of the line $CF.$

Therefore preimages of these lines are concurrent.

vladimir.shelomovskii@gmail.com, vvsss

Sphere and two points

Let a sphere $\omega$ and points $A$ and $B$ be given in space. The line $AB$ does not has the common points with the sphere. The sphere is inscribed in tetrahedron $ABCD.$

Prove that the sum of the angles of the spatial quadrilateral $ACBD$ (i.e. the sum $\angle ACB + \angle CBD + \angle ADB + \angle DAC)$ does not depend on the choice of points $C$ and $D.$

Proof

Denote $K, L, P, Q$ points of tangency $\omega$ and faces of $ABCD$ (see diagram), $\alpha = \angle AQB.$ $AQ = AK = AL, BP = BL = BQ \implies \angle ALB = \alpha.$

It is known that $\angle QBD = \angle PBD, \angle PBC = \angle LBC, \angle LAC = \angle KAC, \angle KAD = QAD.$ $\angle ACB = 180^\circ - \angle CBA - \angle CAB = 180^\circ - (\angle LBC + \angle LBA) - (\angle LAC + \angle LAB) =$ $= (180^\circ - \angle LBA - \angle LAB) - (\angle PBC + \angle KAC) = \alpha - \angle PBC - \angle KAC.$ Similarly, $\angle ADB = \alpha - \angle PBD + \angle KAD.$ $\angle ACB + \angle CBD + \angle ADB + \angle DAC =$ $= (\alpha - \angle PBC - \angle KAC) +(\angle PBC + \angle PBD) + (\alpha - \angle PBD - \angle KAD) + (\angle QAD + \angle QAC) = 2 \alpha,$ The sum not depend on the choice of points $C$ and $D.\blacksquare$

vladimir.shelomovskii@gmail.com, vvsss

Projecting non-convex quadrilateral into rectangle

Let a non-convex quadrilateral $ABCD$ be given. Find a projective transformation of points $A,B,C,D$ into the vertices of rectangle.

Solution

WLOG, point $D$ is inside the $\triangle ABC.$

$E = AB \cap CD, F = BC \cap AD, MF = ME = MS, SM \perp ABC, SE \perp SF.$

Let $SA,SC,SD,$ and $BS$ be the rays, $C'$ be any point on segment $SC.$ $B'C' || SF, B' \in BS, B'A' || SE, A' \in SA, D'C' || SE, D' \in SD.$ Planes $A'B'C'D'$ and $ABCD$ are perpendicular, planes $A'B'C'D'$ and $SEF$ are parallel, so image $EF$ is line at infinity and $A'B'C'D'$ is rectangle.

Let's paint the parts of the planes $ABC$ and $A'B'C'$ that maps into each other with the same color.

$\triangle ADC$ maps into $\triangle A'D'C'$ (yellow).

Green infinite triangle between $AB$ and $BC$ maps into $\triangle PB'Q,$ where plane $SPQ$ is parallel to plane $ABC.$

Blue infinite quadrilateral between $AB$ and $BC$ with side $AC$ maps into quadrilateral $A'C'PQ.$

Therefore inner part of quadrilateral $ABCD$ maps into external part of rectangle $A'B'C'D'.$ For example $\triangle CKL$ maps into $\triangle C'KL$ where $KL || EF$ is the intersection of planes $A'B'C'D'$ and $ABCD.$

Note that the lines through pairs of points (for example, $AB$ ) maps into the corresponding lines, and the intersection point of $AC$ and $BD$ maps into the center of the rectangle.

vladimir.shelomovskii@gmail.com, vvsss

Projecting convex quadrilateral into square

Let $ABCD$ be a convex quadrilateral with no parallel sides.

Find the projective transformation of $ABCD$ into the square $A'B'C'D$ if the angle between the planes $ABD$ and $A'B'D$ is given. This angle is not equal to $0$ or $180^\circ .$

Solution

Denote $E = AB \cap CD, F = BC \cap AD, K = EF \cap BD, L = EF \cap AC.$

Let $S$ be the point satisfying the conditions $\angle ESF = \angle KSL = 90^\circ.$

The locus of such points is the intersection circle of spheres with diameters $EF$ and $KL.$

Let $S$ be the perspector and the image plane be parallel to plane $ESF.$ We use the plane contains $D,$ so image $D' = D.$

Then image $EF$ is the line at infinity, point $E$ is point at infinity, so images $AB$ (line $A'B'$ ) and $CD$ (line $C'D$ ) are parallel to $ES.$

Similarly point $F$ is the point at infinity, so images $A'D || C'B' || FS \implies A'B'C'D$ is the rectangle.

Point $K$ is the point at infinity, so $B'D || KS.$ Point $L$ is the point at infinity, so $A'C' || LS.$

$KS \perp LS \implies A'C' \perp B'D \implies A'B'C'D$ is the square.

Let $M \in EF$ be such point that $SM \perp EF.$

The angle between $SM$ and plane $ABC$ is the angle we can choose. It is equal to the angle between planes $ABC$ and $A'B'C'.$

vladimir.shelomovskii@gmail.com, vvsss

Two lines and two points

Let lines $\ell$ and $\ell_1$ intersecting at point $Q$ , a point $P$ not lying on any of these lines, and points $A$ and $B$ on line $\ell$ be given. $C = BP \cap \ell_1, D = AP \cap \ell_1, E = AC \cap BD.$ Find the locus of points $E.$

Solution

Let $F$ be the point $\ell_1$ such that $BF||QP, M$ be the midpoint $BF.$ Let us prove that the points $Q, E,$ and $M$ are collinear.

The quadrilateral $ABCD$ is convex. We make the projective transformation of $ABCD$ into the square.

Then line $QP$ is the line at infinity, $BF||QP$ so image $M$ is the midpoint of image $BF,$ image $E$ is the center of the square.

Therefore images $\ell = AB, \ell_1 = CD,$ and $EM$ are parallel and points $Q, E,$ and $M$ are collinear.

vladimir.shelomovskii@gmail.com, vvsss

Crossing lines

Let a convex quadrilateral $ABCD$ be given. Denote $F = AB \cap CD, O = AC \cap BD, E = AD \cap BC,$ $K = BC \cap FO, L = AB \cap EO, M = AD \cap FO, N = CD \cap EO.$ Prove that lines $EF, KL,$ and $MN$ are collinear.

Solution

The quadrilateral $ABCD$ is convex.

We make the projective transformation of $ABCD$ into the square.

Then image of the line $EF$ is the line at infinity, image of $O$ is the center of the square.

Images of $EB, ED,$ and $EO$ are parallel, so image $L$ is the midpoint of the image $AB.$ Similarly images of $K, M,$ and $N$ are midpoints of the square sides.

Therefore images $KL$ and $MN$ are parallel, they are crossed at the point in infinity witch lyes at the line at infinity, that is at $EF.$

vladimir.shelomovskii@gmail.com, vvsss

Convex quadrilateral and point

Let a convex quadrilateral $ABCD$ and an arbitrary point $P$ be given, $E = AD \cap BC, F = AB \cap CD, K = BC \cap FP, L = AB \cap EP.$

Prove that lines $CL, AK,$ and $DP$ are concurrent.

Proof

The quadrilateral $ABCD$ is convex. We make the projective transformation of $ABCD$ into the square. Then image of the line $EF$ is the line at infinity, images of $AD, BC$ and $LP$ are parallel. Similarly $AB||CD||KP.$

We use the Cartesian coordinate system with $C(0,0), A(-1,-1), P(a,b).$

Then $L(-1,b), K(a,0).$

So line $CL$ is $y + bx = 0,$ line $AK$ is $y(1 + a) +x - a = 0,$ line $DP$ is $a(y - 1) + x(1 - b) = 0.$

These lines contain point $M \left ( \frac {-a}{1 - b - ab}, \frac {ab}{1 - b - ab} \right ).$

Therefore preimages of $CL, AK,$ and $DP$ are concurrent in preimage of the point $M.$ .

vladimir.shelomovskii@gmail.com, vvsss

Theorem on doubly perspective triangles

Let two triangles $\triangle ABC$ and $\triangle A'B'C'$ be given. Let the lines $AA', BB',$ and $CC'$ be concurrent at point $O,$ and the lines $AB', BC',$ and $CA'$ be concurrent at point $Q.$

Prove that the lines $AC', BA',$ and $CB'$ are concurrent (the theorem on doubly perspective triangles).

Proof

WLOG, the quadrilateral $AA'CC'$ is convex.

We make the projective transformation of $AA'CC'$ into the square.

Then image of the line contains point $O$ is the line at infinity, images of $AA', CC',$ and $BB'$ are parallel. Similarly $AC'||A'C.$

We use the Cartesian coordinate system with $A'(0,0), A(0,1), C'(1,1), C(1,0), B(a,b).$ $Q = BC' \cap A'C \implies Q\left (\frac{b-a}{b-1}, 0 \right ) \implies$ $B' = BB' \cap AQ, \implies B'\left (a, \frac{b-ab}{b-a} \right ).$ So the line $AC'$ is $y = 1,$ line $BA'$ is $a y = bx,$ line $B'C$ is $y(a - b) = b(x - 1).$

These lines contain point $P \left ( \frac {a}{b}, 1 \right ).$

Therefore preimages of $BA', AC',$ and $B'C$ are concurrent in point $P.$ .

vladimir.shelomovskii@gmail.com, vvsss

Complete quadrilateral theorem

Let points $A, B, C, D,$ no three of which are collinear, be given. $P = AD \cap BC, Q = AC \cap BD, E = AB \cap PQ, F = CD \cap PQ.$ Prove that $\frac{QE \cdot PF}{PE \cdot QF} = 1.$

Proof

We make the projective transformation of the vertices of $ABCD$ into vertices of the square. Then image of the point $P$ is the point at infinity, image of $Q$ is the center of the square, images of $AD, PQ,$ and $BC$ are parallel, so for images $QF = QE$ and $\frac {PE}{PF} = 1 \implies \frac{QE \cdot PF}{PE \cdot QF} = 1.$

The double ratio $\frac{QE \cdot PF}{PE \cdot QF}$ is the projective invariant of a quadruple of collinear points $(P,Q;E,F)$ so the equality also holds for the preimages.

vladimir.shelomovskii@gmail.com, vvsss

Medians crosspoint

Let a convex quadrilateral $ABCD$ and line $\ell$ in common position be given (points $A,B,C,$ and $D$ not belong $\ell,$ sides and diagonals are not parallel to $\ell.)$

Denote $P = AB \cap CD, Q = AC \cap BD, R = AD \cap BC,$ $E = BC \cap \ell, E' = AD \cap \ell, F = AB \cap \ell,$ $F' = CD \cap \ell, G = BD \cap \ell, G' = AC \cap \ell.$ Denote $P', Q',$ and $R'$ midpoints of $FF', GG',$ and $EE',$ respectively.

Prove that lines $PP', QQ',$ and $RR'$ are collinear.

Proof

Let the angle $\angle ARB$ be fixed and the line $\ell$ moves in a plane parallel to itself.

Then the line $RR'$ on which the median of the triangle lies is also fixed. Similarly, lines $PP'$ and $QQ'$ are fixed. Denote $T = PP' \cap QQ'.$

Let $\ell$ moves in a plane parallel to itself to the position where $T \in \ell \implies T = P' = Q' \implies EF' = FE'.$

It is known ( Six segments) that $\frac {EG' \cdot GF' \cdot FE'}{GE' \cdot FG' \cdot EF'} = 1 \implies \frac {EG' \cdot GF'}{GE' \cdot FG'} = 1.$

After some simple transformations one can get $GF' = FG' \implies T = R'.$

vladimir.shelomovskii@gmail.com, vvsss

Six segments

Let a convex quadrilateral $ABCD$ and line $\ell$ in common position be given (points $A,B,C,$ and $D$ not belong $\ell,$ sides and diagonals are not parallel to $\ell.)$ Denote $E = BC \cap \ell, E' = AD \cap \ell, F = AB \cap \ell, F' = CD \cap \ell, G = BD \cap \ell, G' = AC \cap \ell.$ Prove that $\frac {FE' \cdot GF' \cdot EG'}{FG' \cdot GE' \cdot EF'} = 1.$

Proof

By applying the law of sines, we get: $\frac{FE'}{\sin \angle BAC}= \frac{AF}{\sin \angle AE'F}, \frac{FG'}{\sin \angle BAC} = \frac{AF}{\sin \angle AG'F} \implies$ $\frac{FE'}{FG'} = \frac {\sin \angle BAD \cdot \sin \angle AG'F}{\sin \angle AE'F \cdot \sin \angle BAC},$ $\frac{GF'}{\sin \angle BDC} = \frac{GD}{\sin \angle CF'F}, \frac{GE'}{\sin \angle ADB} = \frac{GD}{\sin \angle AE'F} \implies \frac{GF'}{GE'} = \frac {\sin \angle BDC \cdot \sin \angle AE'F}{\sin \angle CF'F \cdot \sin \angle ADB},$

$\frac{EG'}{\sin \angle ACB} = \frac{EC}{\sin \angle AG'F}, \frac{EF'}{\sin \angle BCD} = \frac{EC}{\sin \angle CF'F} \implies \frac{EG'}{EF'} = \frac {\sin \angle ACB \cdot \sin \angle CF'F}{\sin \angle AG'F \cdot \sin \angle BCD},$

$\frac {FE' \cdot GF' \cdot EG'}{FG' \cdot GE' \cdot EF'} = \frac{\sin \angle BAC \cdot \sin \angle ADB \cdot \sin \angle BCD}{\sin \angle BCA \cdot \sin \angle BAD \cdot \sin \angle BDC} = 1.$ (see Sines of the angles of a quadrilateral)

vladimir.shelomovskii@gmail.com, vvsss

Sines of the angles of a quadrilateral

Let a convex quadrilateral $ABCD$ be given. Prove that $\frac{\sin \angle BAC \cdot \sin \angle ADB \cdot \sin \angle BCD}{\sin \angle BCA \cdot \sin \angle BAD \cdot \sin \angle BDC} = 1.$

Proof

By applying the law of sines, we get: $\frac{\sin \angle BAC}{\sin \angle BCA} = \frac {BC}{AB}, \frac{\sin \angle ADB}{\sin \angle BAD} = \frac {AB}{BD}, \frac{\sin \angle BCD}{\sin \angle BDC} = \frac {BD}{BC} \implies$ $\frac{\sin \angle BAC \cdot \sin \angle ADB \cdot \sin \angle BCD}{\sin \angle BCA \cdot \sin \angle BAD \cdot \sin \angle BDC} = \frac {BC \cdot AB \cdot BD}{AB \cdot BD \cdot BC} = 1.$

vladimir.shelomovskii@gmail.com, vvsss

Triangle and line

Let triangle $\triangle ABC$ and line $\ell$ be given.

Denote $D = AB \cap \ell, E = BC \cap \ell, F = AC \cap \ell.$

Let $A', B',$ and $C'$ be the points on $\ell$ such that $\frac {DA' \cdot EB' \cdot FC'}{FA' \cdot DB' \cdot EC'} = 1.$

Prove that points $M = AB \cap CC', K = BC \cap AA', L = AC \cap BB'$ are collinear.

Proof

Under projective transformation line $BC$ from point $A$ to $\ell$ points $B,K,C,$ and $E$ maps into points $D, A', F,$ and $E,$ so $(B,C;E,K) = (D,F;E,A') \implies \frac{BE \cdot CK}{BK \cdot CE} = \frac{DE \cdot FA'}{DA' \cdot FE}.$ Similarly, $\frac{BD \cdot AM}{AD \cdot BM} = \frac{DE \cdot C'F}{EC' \cdot DF},$ $\frac{AL \cdot CF}{CL \cdot AF} = \frac{EF \cdot DB'}{EB' \cdot DF}.$

We multiply these three equations and get: $\frac{BE \cdot CK}{BK \cdot CE} \cdot \frac{BD \cdot AM}{AD \cdot BM} \cdot \frac{AL \cdot CF}{CL \cdot AF} = \frac{DE \cdot FA'}{DA' \cdot FE} \cdot \frac{DE \cdot C'F}{EC' \cdot DF} \cdot \frac{EF \cdot DB'}{EB' \cdot DF}.$ We use the Menelaus' theorem for $\triangle ABC$ and a transversal line $\ell$ and get: $\frac{AD \cdot BE \cdot CF}{BD \cdot CE \cdot AF} = 1.$ We make reduction of fractions, we take into account the given condition $\frac {DA' \cdot EB' \cdot FC'}{FA' \cdot DB' \cdot EC'} = 1$ and get: $\frac {AL \cdot BM \cdot CK}{AM \cdot BK \cdot CL} = 1.$ Therefore in accordance with the Menelaus' theorem for $\triangle ABC$ points $M, K,$ and $L$ are collinear.

vladimir.shelomovskii@gmail.com, vvsss

Page

Toolbox

Search

Projective geometry (simplest cases)

Contents

Projection of a circle into a circle

Butterfly theorem

Sharygin’s Butterfly theorem

Semi-inscribed circle

Fixed point

Set of lines

Set of lines in circle and triangle

Projection of any triangle into regular one

Some properties of an equilateral triangle

Two generated triangles

Sphere and two points

Projecting non-convex quadrilateral into rectangle

Projecting convex quadrilateral into square

Two lines and two points

Crossing lines

Convex quadrilateral and point

Theorem on doubly perspective triangles

Complete quadrilateral theorem

Medians crosspoint

Six segments

Sines of the angles of a quadrilateral

Triangle and line