1977 Canadian MO Problems
Revision as of 21:37, 25 July 2006 by Boy Soprano II (talk | contribs)
The seven problems were all on the same day.
Contents
Problem 1
If ![]() prove that the equation
prove that the equation ![]() has no solutions in positive integers
has no solutions in positive integers ![]() and
and ![]()
Problem 2
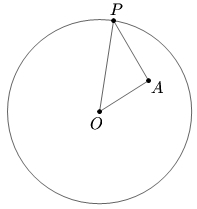
Let ![]() be the center of a circle and
be the center of a circle and ![]() be a fixed interior point of the circle different from
be a fixed interior point of the circle different from ![]() Determine all points
Determine all points ![]() on the circumference of the circle such that the angle
on the circumference of the circle such that the angle ![]() is a maximum.
is a maximum.
Problem 3
![]() is an integer whose representation in base
is an integer whose representation in base ![]() is
is ![]() Find the smallest positive integer
Find the smallest positive integer ![]() for which
for which ![]() is the fourth power of an integer.
is the fourth power of an integer.