Difference between revisions of "2003 AMC 10A Problems"
m (→Problem 1: fixed typo) |
(added problems 21 and 22) |
||
| Line 158: | Line 158: | ||
== Problem 21 == | == Problem 21 == | ||
| + | Pat is to select six cookies from a tray containing only chocolate chip, oatmeal, and peanut butter cookies. There are at least six of each of these three kinds of cookies on the tray. How many different assortments of six cookies can be selected? | ||
| + | |||
| + | <math> \mathrm{(A) \ } 22\qquad \mathrm{(B) \ } 25\qquad \mathrm{(C) \ } 27\qquad \mathrm{(D) \ } 28\qquad \mathrm{(E) \ } 729 </math> | ||
[[2003 AMC 10A Problems/Problem 21|Solution]] | [[2003 AMC 10A Problems/Problem 21|Solution]] | ||
== Problem 22 == | == Problem 22 == | ||
| + | In rectangle <math>ABCD</math>, we have <math>AB=8</math>, <math>BC=9</math>, <math>H</math> is on <math>BC</math> with <math>BH=6</math>, <math>E</math> is on <math>AD</math> with <math>DE=4</math>, line <math>EC</math> intersects line <math>AH</math> at <math>G</math>, and <math>F</math> is on line <math>AD</math> with <math>GF \perp AF</math>. Find the length of <math>GF</math>. | ||
| + | |||
| + | <math> \mathrm{(A) \ } 16\qquad \mathrm{(B) \ } 20\qquad \mathrm{(C) \ } 24\qquad \mathrm{(D) \ } 28\qquad \mathrm{(E) \ } 30 </math> | ||
[[2003 AMC 10A Problems/Problem 22|Solution]] | [[2003 AMC 10A Problems/Problem 22|Solution]] | ||
Revision as of 14:15, 5 November 2006
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
What is the difference between the sum of the first ![]() even counting numbers and the sum of the first
even counting numbers and the sum of the first ![]() odd counting numbers?
odd counting numbers?
![]()
Problem 2
Members of the Rockham Soccer Leauge buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the Leauge?
![]()
Problem 3
A solid box is ![]() cm by
cm by ![]() cm by
cm by ![]() cm. A new solid is formed by removing a cube
cm. A new solid is formed by removing a cube ![]() cm on a side from each corner of this box. What percent of the original volume is removed?
cm on a side from each corner of this box. What percent of the original volume is removed?
![]()
Problem 4
It takes Mary ![]() minutes to walk uphill
minutes to walk uphill ![]() km from her home to school, but it takes her only
km from her home to school, but it takes her only ![]() minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?
minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?
![]()
Problem 5
Let ![]() and
and ![]() denote the solutions of
denote the solutions of ![]() . What is the value of
. What is the value of ![]() ?
?
![]()
Problem 6
Define ![]() to be
to be ![]() for all real numbers
for all real numbers ![]() and
and ![]() . Which of the following statements is not true?
. Which of the following statements is not true?
![]() for all
for all ![]() and
and ![]()
![]() for all
for all ![]() and
and ![]()
![]() for all
for all ![]()
![]() for all
for all ![]()
![]() if
if ![]()
Problem 7
How many non-congruent triangles with perimeter ![]() have integer side lengths?
have integer side lengths?
![]()
Problem 8
What is the probability that a randomly drawn positive factor of ![]() is less than
is less than ![]()
![]()
Problem 9
Simplify
![$\sqrt[3]{x\sqrt[3]{x\sqrt[3]{x\sqrt{x}}}}$](http://latex.artofproblemsolving.com/c/f/2/cf2756b7e9bb76b2adf76f1709cc765535b27602.png) .
.
![]()
Problem 10
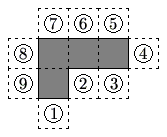
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attatched to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?
![]()
Problem 11
The sum of the two 5-digit numbers ![]() and
and ![]() is
is ![]() . What is
. What is ![]() ?
?
![]()
Problem 12
A point ![]() is randomly picked from inside the rectangle with vertices
is randomly picked from inside the rectangle with vertices ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . What is the probability that
. What is the probability that ![]() ?
?
![]()
Problem 13
The sum of three numbers is ![]() . The first is four times the sum of the other two. The second is seven times the third. What is the product of all three?
. The first is four times the sum of the other two. The second is seven times the third. What is the product of all three?
![]()
Problem 14
Let ![]() be the largest integer that is the product of exactly 3 distinct prime numbers
be the largest integer that is the product of exactly 3 distinct prime numbers ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are single digits. What is the sum of the digits of
are single digits. What is the sum of the digits of ![]() ?
?
![]()
Problem 15
What is the probability that an integer in the set ![]() is divisible by
is divisible by ![]() and not divisible by
and not divisible by ![]() ?
?
![]()
Problem 16
What is the units digit of ![]() ?
?
![]()
Problem 17
The number of inches in the perimeter of an equilateral triangle equals the number of square inches in the area of its circumscribed circle. What is the radius, in inches, of the circle?
![]()
![]()
Problem 18
What is the sum of the reciprocals of the roots of the equation
![]() ?
?
![]()
Problem 19
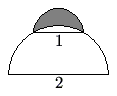
A semicircle of diameter ![]() sits at the top of a semicircle of diameter
sits at the top of a semicircle of diameter ![]() , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.
![]()
Problem 20
A base-10 three digit number ![]() is selected at random. Which of the following is closest to the probability that the base-9 representation and the base-11 representation of
is selected at random. Which of the following is closest to the probability that the base-9 representation and the base-11 representation of ![]() are both thee-digit numerals?
are both thee-digit numerals?
![]()
Problem 21
Pat is to select six cookies from a tray containing only chocolate chip, oatmeal, and peanut butter cookies. There are at least six of each of these three kinds of cookies on the tray. How many different assortments of six cookies can be selected?
![]()
Problem 22
In rectangle ![]() , we have
, we have ![]() ,
, ![]() ,
, ![]() is on
is on ![]() with
with ![]() ,
, ![]() is on
is on ![]() with
with ![]() , line
, line ![]() intersects line
intersects line ![]() at
at ![]() , and
, and ![]() is on line
is on line ![]() with
with ![]() . Find the length of
. Find the length of ![]() .
.
![]()