Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 AMC 12A Problems/Problem 17"

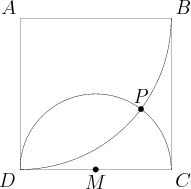
(New page: == Problem == Square <math>ABCD</math> has sides of length <math>4</math>, and <math>M</math> is the midpoint of <math>\overline{CD}</math>. A circle with radius <math>2</math> and center ...)
 
(→‎Problem)
Line 5: Line 5:
  
 
<math>\textbf{(A)}\ 3 \qquad \textbf{(B)}\ \frac {16}{5} \qquad \textbf{(C)}\ \frac {13}{4} \qquad \textbf{(D)}\ 2\sqrt {3} \qquad \textbf{(E)}\ \frac {7}{2}</math>
 
<math>\textbf{(A)}\ 3 \qquad \textbf{(B)}\ \frac {16}{5} \qquad \textbf{(C)}\ \frac {13}{4} \qquad \textbf{(D)}\ 2\sqrt {3} \qquad \textbf{(E)}\ \frac {7}{2}</math>
 +
 +
== Solution ==
 +
 +
Let <math>D</math> be the origin. <math>A</math> is the point <math>(0,4)</math> and <math>M</math> is the point <math>(2,0)</math>. We are given the radius of the quarter circle and semicircle as <math>4</math> and <math>2</math>, respectively, so their equations, respectively, are:
 +
 +
<math>x^2 + (y-4)^2 = 4^2</math>
 +
 +
<math>(x-2)^2 + y^2 = 2^2</math>
 +
 +
 +
Algebraically manipulating the second equation gives:
 +
 +
<math>y^2 = 2^2 - (x-2)^2</math>
 +
 +
<math>y^2 = (2-(x-2)(2+(x-2))</math>
 +
 +
<math>y^2 = (4-x)(x)</math>
 +
 +
<math>y = \sqrt{4x - x^2}</math>
 +
 +
 +
Substituting this back into the first equation:
 +
 +
<math>x^2 + (\sqrt{4x - x^2} - 4)^2 = 4^2</math>
 +
 +
<math>x^2 + 4x - x^2 - 8\sqrt{4x - x^2} + 16 = 16</math>
 +
 +
<math>4x - 8\sqrt{4x - x^2} = 0</math>
 +
 +
<math>4x = 8\sqrt{4x - x^2}</math>
 +
 +
<math>16x^2 = 64(4x - x^2)</math>
 +
 +
<math>16x^2 = 256x - 64x^2</math>
 +
 +
<math>80x^2 - 256x = 0</math>
 +
 +
<math>x(80x - 256) = 0</math>
 +
 +
 +
Solving each factor for 0 yields <math>x = 0 , \frac{16}{5}</math>. The first value of <math>0</math> is obviously referring to the point where the circles intersect at the origin, <math>D</math>, so the second value must be referring to the x value of the coordinate of <math>P</math>. Since <math>\overline{AD}</math> is the y-axis, the distance to it from <math>P</math> is the same as the x-value of the coordinate of <math>P</math>, so the distance from <math>P</math> to <math>\overline{AD}</math> is <math>\frac{16}{5} \Rightarrow B</math>

Revision as of 20:47, 31 May 2008

Problem

Square $ABCD$ has sides of length $4$, and $M$ is the midpoint of $\overline{CD}$. A circle with radius $2$ and center $M$ intersects a circle with raidus $4$ and center $A$ at points $P$ and $D$. What is the distance from $P$ to $\overline{AD}$?

5d50417537c6cddfb70810403c62787b889cdcb1.png

$\textbf{(A)}\ 3 \qquad \textbf{(B)}\ \frac {16}{5} \qquad \textbf{(C)}\ \frac {13}{4} \qquad \textbf{(D)}\ 2\sqrt {3} \qquad \textbf{(E)}\ \frac {7}{2}$

Solution

Let $D$ be the origin. $A$ is the point $(0,4)$ and $M$ is the point $(2,0)$. We are given the radius of the quarter circle and semicircle as $4$ and $2$, respectively, so their equations, respectively, are:

$x^2 + (y-4)^2 = 4^2$

$(x-2)^2 + y^2 = 2^2$


Algebraically manipulating the second equation gives:

$y^2 = 2^2 - (x-2)^2$

$y^2 = (2-(x-2)(2+(x-2))$

$y^2 = (4-x)(x)$

$y = \sqrt{4x - x^2}$


Substituting this back into the first equation:

$x^2 + (\sqrt{4x - x^2} - 4)^2 = 4^2$

$x^2 + 4x - x^2 - 8\sqrt{4x - x^2} + 16 = 16$

$4x - 8\sqrt{4x - x^2} = 0$

$4x = 8\sqrt{4x - x^2}$

$16x^2 = 64(4x - x^2)$

$16x^2 = 256x - 64x^2$

$80x^2 - 256x = 0$

$x(80x - 256) = 0$


Solving each factor for 0 yields $x = 0 , \frac{16}{5}$. The first value of $0$ is obviously referring to the point where the circles intersect at the origin, $D$, so the second value must be referring to the x value of the coordinate of $P$. Since $\overline{AD}$ is the y-axis, the distance to it from $P$ is the same as the x-value of the coordinate of $P$, so the distance from $P$ to $\overline{AD}$ is $\frac{16}{5} \Rightarrow B$

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12A_Problems/Problem_17&oldid=26210"