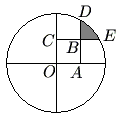
2006 AMC 10B Problems/Problem 19
Problem
A circle of radius ![]() is centered at
is centered at ![]() . Square
. Square ![]() has side length
has side length ![]() . Sides
. Sides ![]() and
and ![]() are extended past
are extended past ![]() to meet the circle at
to meet the circle at ![]() and
and ![]() , respectively. What is the area of the shaded region in the figure, which is bounded by
, respectively. What is the area of the shaded region in the figure, which is bounded by ![]() ,
, ![]() , and the minor arc connecting
, and the minor arc connecting ![]() and
and ![]() ?
?
![]()
Solution
The shaded area is equivilant to the area of sector ![]() minus the area of triangle
minus the area of triangle ![]() plus the area of triangle
plus the area of triangle ![]() .
.
Using the Pythagorean Theorem:
![]()
![]()
Clearly ![]() and
and ![]() are
are ![]() triangles with
triangles with ![]()
Since ![]() is a square,
is a square, ![]()
![]() can be found by doing some subtraction of angles.
can be found by doing some subtraction of angles.
![]()
![]()
![]()
![]()
So the area of sector ![]() is
is ![]()
The area of triangle ![]() is
is ![]()
Since ![]() ,
, ![]()
So the area of triangle ![]() is
is ![]()
Therefore, the shaded area is ![]()