2006 AMC 10B Problems/Problem 6
Problem
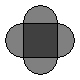
A region is bounded by semicircular arcs constructed on the side of a square whose sides measure ![]() , as shown. What is the perimeter of this region?
, as shown. What is the perimeter of this region?
![]()
Solution
Since the side of the square is the diameter of the semicircle, the radius of the semicircle is ![]()
Since the length of one of the semicircular arcs is half the circumference of the corresponding circle, the length of one arc is ![]()
Since the desired perimeter is made up of four of these arcs, the perimeter is ![]()