Difference between revisions of "2006 AMC 12A Problems/Problem 13"
(added category) |
m (+box, couple of wikilinks) |
||
| Line 3: | Line 3: | ||
[[Image:2006 AMC 12A Problem 13.gif]] | [[Image:2006 AMC 12A Problem 13.gif]] | ||
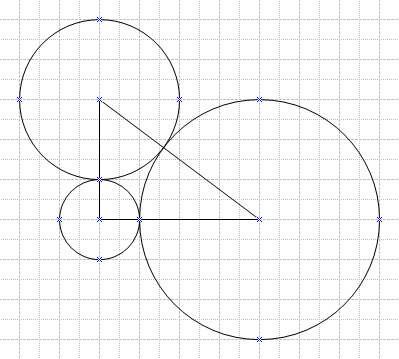
| − | The vertices of a <math>3-4-5</math> right triangle are the centers of three mutually externally tangent | + | The [[vertex|vertices]] of a <math>3-4-5</math> [[right triangle]] are the centers of three mutually externally tangent [[circle]]s, as shown. What is the sum of the areas of the three circles? |
<math> \mathrm{(A) \ } 12\pi\qquad \mathrm{(B) \ } \frac{25\pi}{2}\qquad \mathrm{(C) \ } 13\pi\qquad \mathrm{(D) \ } \frac{27\pi}{2}\qquad\mathrm{(E) \ } 14\pi</math> | <math> \mathrm{(A) \ } 12\pi\qquad \mathrm{(B) \ } \frac{25\pi}{2}\qquad \mathrm{(C) \ } 13\pi\qquad \mathrm{(D) \ } \frac{27\pi}{2}\qquad\mathrm{(E) \ } 14\pi</math> | ||
| Line 9: | Line 9: | ||
== Solution == | == Solution == | ||
| − | Let the radius of the smallest circle be <math> a </math>. We find that the radius of the largest circle is <math>4-a</math> and the radius of the second largest circle is <math>3-a</math>. Thus, <math>4-a+3-a=5\iff a=1</math>. The radii of the other circles are <math>3</math> and <math>2</math>. The sum of their areas is <math>\pi+9\pi+4\pi=14\pi\iff\mathrm{(E)}</math> | + | Let the radius of the smallest circle be <math> a </math>. We find that the [[radius]] of the largest circle is <math>4-a</math> and the radius of the second largest circle is <math>3-a</math>. Thus, <math>4-a+3-a=5\iff a=1</math>. The radii of the other circles are <math>3</math> and <math>2</math>. The sum of their areas is <math>\pi+9\pi+4\pi=14\pi\iff\mathrm{(E)}</math> |
== See also == | == See also == | ||
* [[2006 AMC 12A Problems]] | * [[2006 AMC 12A Problems]] | ||
| − | + | ||
| − | + | {{AMC box|year=2006|n=12A|num-b=13|num-a=15}} | |
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
Revision as of 19:45, 31 January 2007
Problem
The vertices of a ![]() right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
![]()
Solution
Let the radius of the smallest circle be ![]() . We find that the radius of the largest circle is
. We find that the radius of the largest circle is ![]() and the radius of the second largest circle is
and the radius of the second largest circle is ![]() . Thus,
. Thus, ![]() . The radii of the other circles are
. The radii of the other circles are ![]() and
and ![]() . The sum of their areas is
. The sum of their areas is ![]()
See also
| {{{header}}} | ||
| Preceded by Problem 13 |
AMC 12A 2006 |
Followed by Problem 15 |