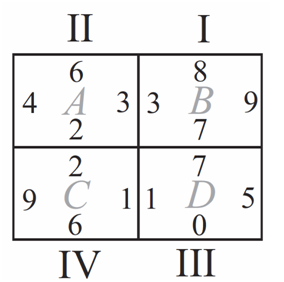
2007 AMC 8 Problems/Problem 11
Problem
Tiles ![]() and
and ![]() are translated so one tile coincides with each of the rectangles
are translated so one tile coincides with each of the rectangles ![]() and
and ![]() . In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle
. In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle ![]() ?
?

![]() cannot be determined
cannot be determined
Solution
We first notice that tile III has a ![]() on the bottom and a
on the bottom and a ![]() on the right side. Since no other tile has a
on the right side. Since no other tile has a ![]() or a
or a ![]() , Tile III must be in rectangle
, Tile III must be in rectangle ![]() . Tile III also has a
. Tile III also has a ![]() on the left, so Tile IV must be in Rectangle
on the left, so Tile IV must be in Rectangle ![]() .
.
The answer is ![]()