Difference between revisions of "2010 AMC 10B Problems/Problem 16"
| Line 1: | Line 1: | ||
| − | + | The radius of circle is <math>\frac{\sqrt{3}}{3} = \sqrt{\frac{1}{3}}</math> | |
| − | Half the diagonal of the square | + | Half the diagonal of the square is <math>\frac{\sqrt{1^2+1^2}}{2} = \frac{\sqrt{2}}{2}</math>. We can see that the circle passes outside the square, but the square is NOT completely contained in the circle |
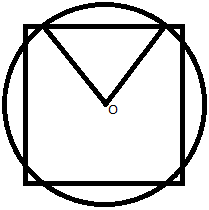
Therefore the picture will look something like this: | Therefore the picture will look something like this: | ||
| Line 7: | Line 7: | ||
[[Image:squarecircle.png]] | [[Image:squarecircle.png]] | ||
| − | Then | + | Then we proceed to find: 4 * (area of the sector marked off by the two radii drawn - area of the triangle with side on the square and the two radii). |
| + | |||
| + | |||
| + | To find this, we do the following: | ||
| + | |||
| + | First we realize that the radius perpendicular to the side of the square between the extra lines marking off the sector splits the chord in half. Let this half-length be <math>a</math>. Power of a point states that if two chords (AB and CD) intersect at X, then AX<math>\cdot</math>BX<math>=</math>CX<math>\cdot</math>DX. Applying power of a point to this situation, <math>a^2=(\frac{\sqrt{3}}{3}-\frac{1}{2})(\frac{\sqrt{3}}{3}+\frac{1}{2})</math>. (We know the center of a square to be halfway in each direction, if you know what I mean by direction). | ||
| + | |||
| + | Solving, <math>a= \frac{\sqrt{3}}{6}</math>. The significance? This means the chord is equal to the radius of a circle, so the sector has angle <math>60^{\circ}</math>. Since this is a sixth of the circle, the sector has area <math>\frac{\pi}{6}\cdot \frac{\sqrt{3}}{3}^2=\frac{\pi}{18}</math>. | ||
| + | |||
| + | Now we turn to the triangle. | ||
| + | |||
| + | Since it is equilateral, we know it has area equal to <math>\frac{\sqrt{3}}{4}</math> times the square of its sidelength. Therefore, our triangle has area <math>\frac{\frac{\sqrt{3}}{3}^2\sqrt{3}}{4}=\frac{\sqrt{3}}{12}</math>. | ||
| + | |||
| + | Putting it together, we get the answer to be <math>4\left( \frac{\pi}{18}-\frac{\sqrt{3}{12} \right)=</math> | ||
| + | |||
| + | <cmath>\frac{2\pi}{9}-\frac{\sqrt{3}}{3} (B)</cmath> | ||
| + | |||
| + | == See also == | ||
| + | [[Area of an equilateral triangle]] | ||
Revision as of 18:28, 12 June 2011
The radius of circle is ![]()
Half the diagonal of the square is ![]() . We can see that the circle passes outside the square, but the square is NOT completely contained in the circle
. We can see that the circle passes outside the square, but the square is NOT completely contained in the circle
Therefore the picture will look something like this:
Then we proceed to find: 4 * (area of the sector marked off by the two radii drawn - area of the triangle with side on the square and the two radii).
To find this, we do the following:
First we realize that the radius perpendicular to the side of the square between the extra lines marking off the sector splits the chord in half. Let this half-length be ![]() . Power of a point states that if two chords (AB and CD) intersect at X, then AX
. Power of a point states that if two chords (AB and CD) intersect at X, then AX![]() BX
BX![]() CX
CX![]() DX. Applying power of a point to this situation,
DX. Applying power of a point to this situation, ![]() . (We know the center of a square to be halfway in each direction, if you know what I mean by direction).
. (We know the center of a square to be halfway in each direction, if you know what I mean by direction).
Solving, ![]() . The significance? This means the chord is equal to the radius of a circle, so the sector has angle
. The significance? This means the chord is equal to the radius of a circle, so the sector has angle ![]() . Since this is a sixth of the circle, the sector has area
. Since this is a sixth of the circle, the sector has area ![]() .
.
Now we turn to the triangle.
Since it is equilateral, we know it has area equal to ![]() times the square of its sidelength. Therefore, our triangle has area
times the square of its sidelength. Therefore, our triangle has area ![]() .
.
Putting it together, we get the answer to be $4\left( \frac{\pi}{18}-\frac{\sqrt{3}{12} \right)=$ (Error compiling LaTeX. Unknown error_msg)
![]()