Difference between revisions of "2011 AIME II Problems/Problem 8"
(→Solution 1.\overline{6}) |
|||
| (34 intermediate revisions by 18 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Problem | + | == Problem == |
| − | Let <math> | + | Let <math>z_1,z_2,z_3,\dots,z_{12}</math> be the 12 zeroes of the polynomial <math>z^{12}-2^{36}</math>. For each <math>j</math>, let <math>w_j</math> be one of <math>z_j</math> or <math>i z_j</math>. Then the maximum possible value of the real part of <math>\sum_{j=1}^{12} w_j</math> can be written as <math>m+\sqrt{n}</math> where <math>m</math> and <math>n</math> are positive integers. Find <math>m+n</math>. |
| − | ---- | + | == Solution == |
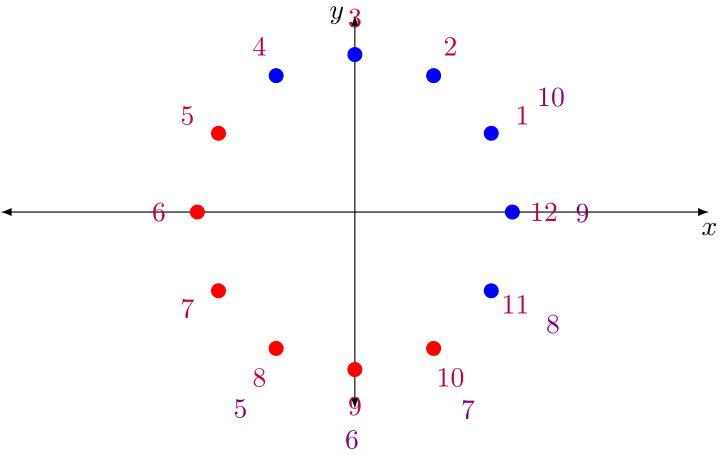
| − | Solution: | + | <center>[[File:2011_AIME_II_-8.png]]</center> |
| + | |||
| + | The twelve dots above represent the <math>12</math> roots of the equation <math>z^{12}-2^{36}=0</math>. If we write <math>z=a+bi</math>, then the real part of <math>z</math> is <math>a</math> and the real part of <math>iz</math> is <math>-b</math>. The blue dots represent those roots <math>z</math> for which the real part of <math>z</math> is greater than the real part of <math>iz</math>, and the red dots represent those roots <math>z</math> for which the real part of <math>iz</math> is greater than the real part of <math>z</math>. Now, the sum of the real parts of the blue dots is easily seen to be <math>8+16\cos\frac{\pi}{6}=8+8\sqrt{3}</math> and the negative of the sum of the imaginary parts of the red dots is easily seen to also be <math>8+8\sqrt{3}</math>. Hence our desired sum is <math>16+16\sqrt{3}=16+\sqrt{768}</math>, giving the answer <math>\boxed{784}.</math> | ||
| + | |||
| + | === Solution <math>1.\overline{3}</math> === | ||
| + | |||
| + | As a small note, we could factor the equation as <math>z^{12} = 2^{36} \implies (\frac{z}{8})^{12} = 1</math> in which these are just the 12th roots of unity for <math>\frac{z}{8}</math> which might be easier to work with. Then we just add up the optimal real parts as in solution 1 and then multiply by 8 at the end. | ||
| + | |||
| + | === Solution <math>1.\overline{6}</math> === | ||
| + | |||
| + | Note that <math>\sin(x) = \sin(x + \pi/2 - \pi/2) = \cos(x + \pi/2)</math>. | ||
| + | |||
| + | So, one can easily translate all the red dots by <math>90^{\circ}</math>. | ||
| + | |||
| + | [[File:Red Point Translation.png]] | ||
| + | |||
| + | Then, it's easy to see that points 2, 3, and 4 cancel out with 5, 6, and 7, so you're left with <math>8 \cdot (\cos \pi/6 + \cos -\pi/6 + \cos 0)</math> times two | ||
| + | ~[https://artofproblemsolving.com/wiki/index.php?title=User:Crazyvideogamez CrazyVideoGamez] | ||
| + | |||
| + | == Solution 2 == | ||
| + | |||
| + | The equation <math>z^{12}-2^{36}=0</math> can be factored as follows: | ||
| + | <cmath>(z^6-2^{18})(z^6+2^{18})=0</cmath> | ||
| + | <cmath>(z^2-2^6)(z^2+2^6)({(z^2+2^6)}^2-z^2\cdot2^6)({(z^2-2^6)}^2+z^2\cdot2^6)=0</cmath> | ||
| + | <cmath>(z^2-2^6)(z^2+2^6)(z^2+2^6-z\cdot2^3)(z^2+2^6+z\cdot2^3) (z^2-2^6-iz\cdot2^3)(z^2-2^6+i z\cdot2^3)=0</cmath> | ||
| + | |||
| + | Since this is a 12th degree equation, there are 12 roots. Also, since each term in the equation is even, the positive or negative value of each root is another root. That would mean there are 6 roots that can be multiplied by <math>-1</math> and since we have 6 factors, that’s 1 root per factor. We just need to solve for <math>z</math> in each factor and pick whether or not to multiply by <math>i</math> and <math>-1</math> for each one depending on the one that yields the highest real value. After that process, we get <math>8+8+2((4\sqrt{3}+4)+(4\sqrt{3}-4))</math> Adding the values up yields <math>16+16\sqrt{3}</math>, or <math>16+\sqrt{768}</math>, and <math>16+768=\boxed{784}</math>. | ||
| + | |||
| + | -Solution by Someonenumber011. | ||
| + | |||
| + | == Solution 3 == | ||
| + | Clearly, the roots are: <math>2^3*(\cos{\frac{k\pi}{12}}+i\sin{\frac{k\pi}{12}}), k\in{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}</math>. | ||
| + | |||
| + | Now, realize for <math>z=a+bi</math>, <math>\operatorname{Re}(iz)=-b</math>. <math>\operatorname{Re}(z)=a</math>. <math>\operatorname{Re}(z)<\operatorname{Re}(iz)</math> is true when <math>a<-b</math>. | ||
| + | |||
| + | This means: | ||
| + | |||
| + | When <math>a>0</math>, <math>b<-a<0</math>. | ||
| + | |||
| + | When <math>a<0</math>, <math>0<b<-a</math>. | ||
| + | |||
| + | For the 12 roots of the polynomial in the original equation, <math>8\cos{k\pi/12}=\operatorname{Re}(z), k\in{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}</math>. <math>-8\sin{k\pi/12}=\operatorname{Im}(iz), k\in{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}</math>. | ||
| + | |||
| + | So <math>8\cos{k\pi/12}<-8\sin{k\pi/12}</math>. <math>-\cos{k\pi/12}>\sin{k\pi/12}</math>. This can be easily true for roots that are in the 3rd quadrant in the complex plane. | ||
| + | |||
| + | This cannot be true for roots in the 1st quadrant because that would yield a negative number bigger than a positive one. | ||
| + | |||
| + | Consider the roots in the 2nd and 4th quadrants. Calculate the roots, choose, and then add the ones up. You will get <math>\boxed{784}</math>. | ||
| + | |||
| + | ~hastapasta | ||
| + | |||
| + | == Solution 4 (Brute Force)== | ||
| + | |||
| + | Use De Moivre's Theorem to brute force all the roots out. Then choose the greater value of <math>\operatorname{Re}(z), \operatorname{Re}(iz)</math>. After adding everything up, you get <math>\boxed{784}</math>. | ||
| + | |||
| + | ~hastapasta | ||
| + | |||
| + | ==See also== | ||
| + | {{AIME box|year=2011|n=II|num-b=7|num-a=9}} | ||
| + | |||
| + | [[Category:Intermediate Algebra Problems]] | ||
| + | [[Category:Complex Number Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 18:46, 27 January 2024
Contents
Problem
Let ![]() be the 12 zeroes of the polynomial
be the 12 zeroes of the polynomial ![]() . For each
. For each ![]() , let
, let ![]() be one of
be one of ![]() or
or ![]() . Then the maximum possible value of the real part of
. Then the maximum possible value of the real part of ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Solution
The twelve dots above represent the ![]() roots of the equation
roots of the equation ![]() . If we write
. If we write ![]() , then the real part of
, then the real part of ![]() is
is ![]() and the real part of
and the real part of ![]() is
is ![]() . The blue dots represent those roots
. The blue dots represent those roots ![]() for which the real part of
for which the real part of ![]() is greater than the real part of
is greater than the real part of ![]() , and the red dots represent those roots
, and the red dots represent those roots ![]() for which the real part of
for which the real part of ![]() is greater than the real part of
is greater than the real part of ![]() . Now, the sum of the real parts of the blue dots is easily seen to be
. Now, the sum of the real parts of the blue dots is easily seen to be ![]() and the negative of the sum of the imaginary parts of the red dots is easily seen to also be
and the negative of the sum of the imaginary parts of the red dots is easily seen to also be ![]() . Hence our desired sum is
. Hence our desired sum is ![]() , giving the answer
, giving the answer ![]()
Solution 
As a small note, we could factor the equation as ![]() in which these are just the 12th roots of unity for
in which these are just the 12th roots of unity for ![]() which might be easier to work with. Then we just add up the optimal real parts as in solution 1 and then multiply by 8 at the end.
which might be easier to work with. Then we just add up the optimal real parts as in solution 1 and then multiply by 8 at the end.
Solution 
Note that ![]() .
.
So, one can easily translate all the red dots by ![]() .
.
Then, it's easy to see that points 2, 3, and 4 cancel out with 5, 6, and 7, so you're left with ![]() times two
~CrazyVideoGamez
times two
~CrazyVideoGamez
Solution 2
The equation ![]() can be factored as follows:
can be factored as follows:
![]()
![]()
![]()
Since this is a 12th degree equation, there are 12 roots. Also, since each term in the equation is even, the positive or negative value of each root is another root. That would mean there are 6 roots that can be multiplied by ![]() and since we have 6 factors, that’s 1 root per factor. We just need to solve for
and since we have 6 factors, that’s 1 root per factor. We just need to solve for ![]() in each factor and pick whether or not to multiply by
in each factor and pick whether or not to multiply by ![]() and
and ![]() for each one depending on the one that yields the highest real value. After that process, we get
for each one depending on the one that yields the highest real value. After that process, we get ![]() Adding the values up yields
Adding the values up yields ![]() , or
, or ![]() , and
, and ![]() .
.
-Solution by Someonenumber011.
Solution 3
Clearly, the roots are: ![]() .
.
Now, realize for ![]() ,
, ![]() .
. ![]() .
. ![]() is true when
is true when ![]() .
.
This means:
When ![]() ,
, ![]() .
.
When ![]() ,
, ![]() .
.
For the 12 roots of the polynomial in the original equation, ![]() .
. ![]() .
.
So ![]() .
. ![]() . This can be easily true for roots that are in the 3rd quadrant in the complex plane.
. This can be easily true for roots that are in the 3rd quadrant in the complex plane.
This cannot be true for roots in the 1st quadrant because that would yield a negative number bigger than a positive one.
Consider the roots in the 2nd and 4th quadrants. Calculate the roots, choose, and then add the ones up. You will get ![]() .
.
~hastapasta
Solution 4 (Brute Force)
Use De Moivre's Theorem to brute force all the roots out. Then choose the greater value of ![]() . After adding everything up, you get
. After adding everything up, you get ![]() .
.
~hastapasta
See also
| 2011 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.