2017 IMO Problems/Problem 4
Let ![]() and
and ![]() be different points on a circle
be different points on a circle ![]() such that
such that ![]() is not a diameter. Let
is not a diameter. Let ![]() be the tangent line to
be the tangent line to ![]() at
at ![]() . Point
. Point ![]() is such that
is such that ![]() is the midpoint of the line segment
is the midpoint of the line segment ![]() . Point
. Point ![]() is chosen on the shorter arc
is chosen on the shorter arc ![]() of
of ![]() so that the circumcircle
so that the circumcircle ![]() of triangle
of triangle ![]() intersects
intersects ![]() at two distinct points. Let
at two distinct points. Let ![]() be the common point of
be the common point of ![]() and
and ![]() that is closer to
that is closer to ![]() . Line
. Line ![]() meets
meets ![]() again at
again at ![]() . Prove that the line
. Prove that the line ![]() is tangent to
is tangent to ![]() .
.
Solution
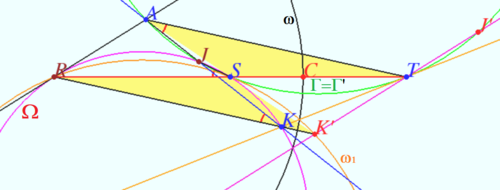
We construct inversion which maps ![]() into the circle
into the circle ![]() and
and ![]() into
into ![]() Than we prove that
Than we prove that ![]() is tangent to
is tangent to ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
We construct circle ![]() centered at
centered at ![]() which maps
which maps ![]() into
into ![]()
Let ![]() Inversion with respect to
Inversion with respect to ![]() swap
swap ![]() and
and ![]() maps into
maps into ![]()
Let ![]() be the center of
be the center of ![]()
Inversion with respect to ![]() maps
maps ![]() into
into ![]() .
.
![]() belong
belong ![]() circle
circle ![]() is the image of
is the image of ![]() . Let
. Let ![]() be the center of
be the center of ![]()
![]() is the image of
is the image of ![]() at this inversion,
at this inversion, ![]() is tangent line to
is tangent line to ![]() at
at ![]() so
so ![]()
![]() is image K at this inversion
is image K at this inversion ![]() is parallelogram.
is parallelogram.
![]() is the midpoint of
is the midpoint of ![]() is the center of symmetry of
is the center of symmetry of ![]()
![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]()
![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]()
![]() is symmetrycal
is symmetrycal ![]() with respect to
with respect to ![]()
![]() lies on
lies on ![]() and on
and on ![]() is tangent to
is tangent to ![]() line
line ![]() is tangent to
is tangent to ![]()
vladimir.shelomovskii@gmail.com, vvsss
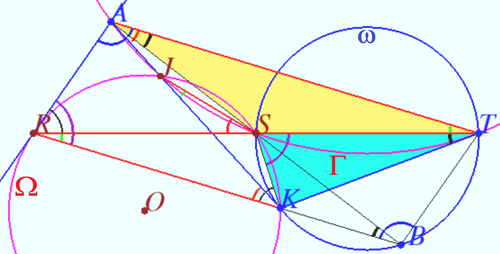
Solution 2
We use the tangent-chord theorem: the angle formed between a chord and a tangent line to a circle is equal to the inscribed angle on the other side of the chord.
Quadrangle ![]() is cyclic
is cyclic ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
![]()
(One can use Reim’s theorem – it is shorter way.)
Let ![]() be symmetric to
be symmetric to ![]() with respect to
with respect to ![]()
![]() is parallelogram.
is parallelogram.
![]()
![]()
![]() is cyclic.
is cyclic.
![]()
Inscribed angle of ![]() is equal to angle between
is equal to angle between ![]() and chord
and chord ![]()
![]() is tangent to
is tangent to ![]() by the inverse of tangent-chord theorem.
by the inverse of tangent-chord theorem.
vladimir.shelomovskii@gmail.com, vvsss