2017 USAMO Problems/Problem 3
Problem
Let ![]() be a scalene triangle with circumcircle
be a scalene triangle with circumcircle ![]() and incenter
and incenter ![]() Ray
Ray ![]() meets
meets ![]() at
at ![]() and
and ![]() again at
again at ![]() the circle with diameter
the circle with diameter ![]() cuts
cuts ![]() again at
again at ![]() Lines
Lines ![]() and
and ![]() meet at
meet at ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() The circumcircles of
The circumcircles of ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]() Prove that
Prove that ![]() passes through the midpoint of either
passes through the midpoint of either ![]() or
or ![]()
Solution
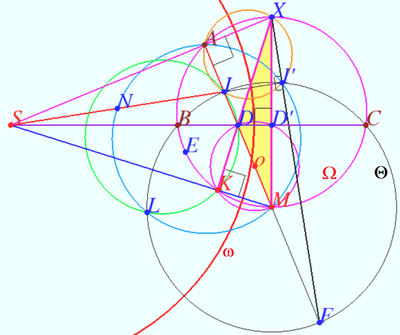
Let ![]() be the point on circle
be the point on circle ![]() opposite
opposite ![]() . This means
. This means ![]()
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Let ![]()
![]() is the orthocenter of
is the orthocenter of ![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
We denote ![]() inversion with respect to
inversion with respect to ![]()
Note that the circle ![]() has diameter
has diameter ![]() and contain points
and contain points ![]() and
and ![]()
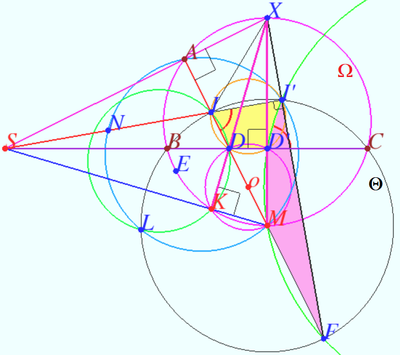
![]() circle
circle ![]()
![]() circle
circle ![]()
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Let ![]() It is well known that
It is well known that ![]()
![]() is circle centered at
is circle centered at ![]()
![]()
Let ![]()
![]() is cyclic.
is cyclic.
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic.
is cyclic.
Therefore point ![]() lies on
lies on ![]()
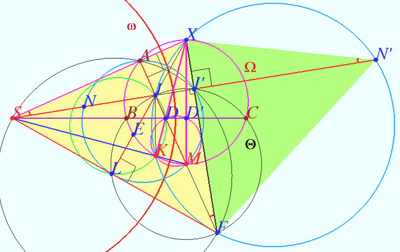
![]() is orthocenter of
is orthocenter of ![]()
![]() is midpoint
is midpoint ![]() is midpoint
is midpoint ![]() is orthocenter of
is orthocenter of ![]() is root of height
is root of height ![]() is the nine-point circle of
is the nine-point circle of ![]()
Let ![]()
![]()
![]() is cyclic.
is cyclic.
Therefore point ![]() lies on
lies on ![]()
The points ![]() and
and ![]() are collinear,
are collinear, ![]() is cyclic.
is cyclic.
Point ![]() is orthocenter
is orthocenter ![]()
![]() The points
The points ![]() and
and ![]() are collinear.
are collinear.
![]() is circle
is circle ![]()
![]() is cyclic.
is cyclic.
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Contact
Contact v_Enhance at https://www.facebook.com/v.Enhance.
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()