2021 AIME I Problems/Problem 11
Problem
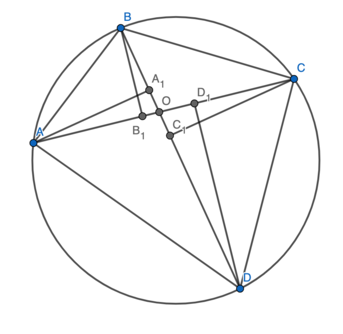
Let ![]() be a cyclic quadrilateral with
be a cyclic quadrilateral with ![]() and
and ![]() . Let
. Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() , respectively, to line
, respectively, to line ![]() and let
and let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to line
respectively, to line ![]() . The perimeter of
. The perimeter of ![]() is
is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Let
. Let ![]() .
.
Firstly, since ![]() , we deduce that
, we deduce that ![]() is cyclic. This implies that
is cyclic. This implies that ![]() , with a ratio of
, with a ratio of ![]() . This means that
. This means that ![]() . Similarly,
. Similarly, ![]() . Hence
. Hence ![]() It therefore only remains to find
It therefore only remains to find ![]() .
.
From Ptolemy's theorem, we have that ![]() . From Brahmagupta's Formula,
. From Brahmagupta's Formula, ![]() . But the area is also
. But the area is also ![]() , so
, so ![]() . Then the desired fraction is
. Then the desired fraction is ![]() for an answer of
for an answer of ![]() .
.
See also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.