2021 JMPSC Sprint Problems/Problem 13
Contents
Problem
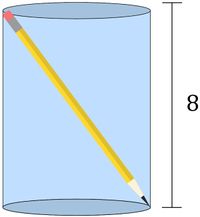
Grace places a pencil in a cylindrical cup and is surprised to see that it fits diagonally. The pencil is ![]() units long and of negligible thickness. The cup is
units long and of negligible thickness. The cup is ![]() units tall. The volume of the cup can be written as
units tall. The volume of the cup can be written as ![]() cubic units. Find
cubic units. Find ![]() .
.
Solution
By the Pythagorean Theorem, we have that the diameter of the cylinder's base is 15 units long. Thus, the cylinder's base has radius ![]() units. Thus, the volume of the cylinder is
units. Thus, the volume of the cylinder is ![]()
~Lamboreghini
Solution 2
The diameter is ![]() . Therefore,
. Therefore,
![]() So,
So, ![]()
- kante314 -
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.