2021 JMPSC Sprint Problems/Problem 16
Contents
Problem
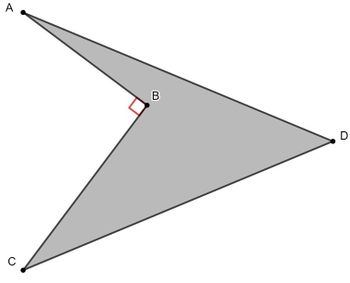
![]() is a concave quadrilateral with
is a concave quadrilateral with ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Find the area of
. Find the area of ![]() .
.
Solution
Notice that ![]() and
and ![]() by the Pythagorean Thereom. We then have that the area of triangle of
by the Pythagorean Thereom. We then have that the area of triangle of ![]() is
is ![]() , and the area of triangle
, and the area of triangle ![]() is
is ![]() , so the area of quadrilateral
, so the area of quadrilateral ![]() is
is ![]() .
.
~Mathdreams
Solution 2
![]()
![]() Therefore,
Therefore, ![]()
- kante314 -
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.