Difference between revisions of "2021 JMPSC Sprint Problems/Problem 3"
(→Problem) |
|||
| Line 6: | Line 6: | ||
==Solution== | ==Solution== | ||
| − | + | ||
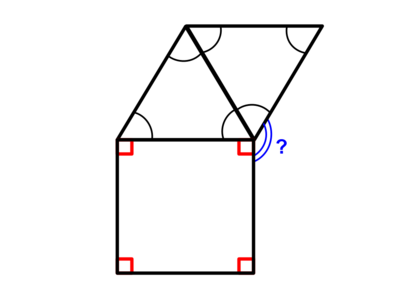
| + | It is given that the right angles are <math>90</math> degrees, and that all the angles in the two triangles are all equal. We can already infer that the black angles are all <math>60</math> degrees, since they are equilateral triangles. | ||
| + | |||
| + | There are <math>360</math> degrees in a whole circle. We are given two of the black curves, and a <math>90</math> degree angle, in which all three of them add up to <math>210</math> degrees. | ||
| + | |||
| + | <math>360-210=150</math>. Therefore, the angle marked with a question mark has a measure of <math>150</math> degrees. | ||
Revision as of 00:50, 11 July 2021
Problem
If all angles marked with a red square are ![]() and all angles marked with one black curve are equal, find the measure of the angle with a question mark.
and all angles marked with one black curve are equal, find the measure of the angle with a question mark.
Solution
It is given that the right angles are ![]() degrees, and that all the angles in the two triangles are all equal. We can already infer that the black angles are all
degrees, and that all the angles in the two triangles are all equal. We can already infer that the black angles are all ![]() degrees, since they are equilateral triangles.
degrees, since they are equilateral triangles.
There are ![]() degrees in a whole circle. We are given two of the black curves, and a
degrees in a whole circle. We are given two of the black curves, and a ![]() degree angle, in which all three of them add up to
degree angle, in which all three of them add up to ![]() degrees.
degrees.
![]() . Therefore, the angle marked with a question mark has a measure of
. Therefore, the angle marked with a question mark has a measure of ![]() degrees.
degrees.