2022 AMC 10A Problems/Problem 25
Problem 25
Let ![]() ,
, ![]() , and
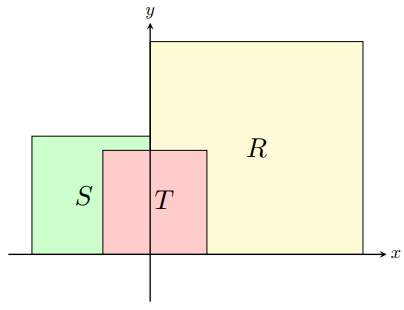
, and ![]() be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the x-axis. The left edge of
be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the x-axis. The left edge of ![]() and the right edge of
and the right edge of ![]() are on the
are on the ![]() -axis, and
-axis, and ![]() contains
contains ![]() as many lattice points as does
as many lattice points as does ![]() . The top two vertices of
. The top two vertices of ![]() are in
are in ![]() , and
, and ![]() contains
contains ![]() of the lattice points contained in
of the lattice points contained in ![]() . See the figure (not drawn to scale).
. See the figure (not drawn to scale).
The fraction of lattice points in ![]() that are in
that are in ![]() is 27 times the fraction of lattice points in
is 27 times the fraction of lattice points in ![]() that are in
that are in ![]() . What is the minimum possible value of the edge length of
. What is the minimum possible value of the edge length of ![]() plus the edge length of
plus the edge length of ![]() plus the edge length of
plus the edge length of ![]() ?
?
![]()
Solution
Let ![]() be the number of lattice points on the side length of square
be the number of lattice points on the side length of square ![]() ,
, ![]() be the number of lattice points on the side length of square
be the number of lattice points on the side length of square ![]() , and
, and ![]() be the number of lattice points on the side length of square
be the number of lattice points on the side length of square ![]() . Note that the actual lengths of the side lengths are the number of lattice points minus
. Note that the actual lengths of the side lengths are the number of lattice points minus ![]() , so we can work in terms of
, so we can work in terms of ![]() and subtract
and subtract ![]() to get the actual answer at the end. Furthermore, note that the number of lattice points inside a rectangular region is equal to the number of lattice points in its width times the number of lattice points along its length.
to get the actual answer at the end. Furthermore, note that the number of lattice points inside a rectangular region is equal to the number of lattice points in its width times the number of lattice points along its length.
Using this fact, the number of lattice points in ![]() is
is ![]() , the number of lattice points in
, the number of lattice points in ![]() is
is ![]() , and the number of lattice points in
, and the number of lattice points in ![]() is
is ![]() .
Solution in progress
.
Solution in progress
~KingRavi
See Also
| 2022 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by [[2022 AMC 10A Problems/Problem {{{num-a}}}|Problem {{{num-a}}}]] | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.