Difference between revisions of "Basic Programming With Python"
m (→Why Are Datatypes So Important?: BUG) |
(→Why Are Datatypes So Important?: floats) |
||
| Line 608: | Line 608: | ||
If you run this, you will get 5, which is correct. | If you run this, you will get 5, which is correct. | ||
| + | |||
| + | Here's another reason datatypes are important. Now, we will introduce the datatype called the '''floating point number''', or '''float'''. A floating point number is a number with a decimal point. | ||
| + | |||
| + | Let's go back to the IDLE. Type "0.1*10". The result is 1.0. Notice the decimal point. | ||
| + | |||
| + | Let's type something different. Type <math>0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1.</math> | ||
| + | |||
| + | '''WHAT!?''' | ||
| + | |||
| + | You would have expected the answer to be 1, but it isn't 1. What happened? | ||
| + | |||
| + | '''Float approximation''' happened. Most (almost all) programming languages have a bad float approximation. That means that 1.0 can turn into 0.99999999999999 and 0.5 can turn into 0.49999999999999999993. That only happens with floats, so we should try to use floats as sparingly as possible. | ||
Revision as of 16:54, 13 March 2018
Important: It is extremely recommended that you read Getting Started With Python Programming before reading this unless you already know some programming knowledge.
This article will talk about some basic Python programming. If you don't even know how to install Python, look here.
Note that this article has lots of program examples. It is recommended (but not required) to try these on your own before looking at the solutions.
Contents
[hide]Loops
There are two different kinds of loops in Python: the for loop and the while loop.
The For Loop
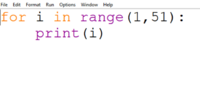
The for loop iterates over a list, or an array, of objects. You have probably seen this code before:
This for loop iterates over the list of integers from 1 to 51, excluding the 51 and including the 1. That means it is a list from 1 to 50, inclusive. On every iteration, Python will print the number that the loop is iterating through.
For example, in the first iteration, i = 1, so Python prints 1.
In the second iteration, i = 2, so Python prints 2.
This continues so on until the number, 50, is reached. Therefore, the last number Python will print out is 50.
Program Example
Find 
To do this task, we must create a for loop and loop over the integers from 1 to 50 inclusive:
for i in range(1,51):
Now what? We must keep a running total and increase it by ![]() every time:
every time:
total = 0
for i in range(1,51):
- total += 2**i
We must not forget to print the total at the end!
total = 0
for i in range(1,51):
- total += 2**i
print(total)
You must exit out of the for loop one you reach the print(total) line by pressing backspace.
Once you run your program, you should get an answer of ![]()
The While Loop
While loops don't loop over a list. They loop over and over and over...until...a condition becomes false.
i = 3
total = 0
while i < 1000:
- total += i
- i += 3
print(total)
In this code, the while loop loops 333 times, until i becomes greater than or equal to 1000.
Program Example
Find ![]() using a while loop.
using a while loop.
We must create a while loop that will iterate until n is greater than ![]()
n = 1
total = 0
while n <= 50:
- total += 2**n
- n += 1
print(total)
We must not forget to include the n += 1 line at the end of the while loop!
If we run this, we will get the same answer as last time, ![]()
Functions
In this section, we will define new operations and do arithmetic with them in Python.
The New Operation
Let's say that you defined a new binary operation, the ![]() You want it to be so
You want it to be so ![]() Therefore,
Therefore, ![]() and
and ![]() Let's call this operation an up down arrow.
Let's call this operation an up down arrow.
Program Example 1
Find ![]()
We know this will be a big number, so we should write a program to do it! We certainly don't want to do the exponentiation and multiplication every time we use the operation in our program, and that's where functions come in! Functions can take in parameters (![]() and
and ![]() ) and return a result depending on the parameters.
) and return a result depending on the parameters.
def up_down_arrow(a,b):
- return ((a**b) * (b**a))
Above is the code to define our function. We need to print the final result at the end, so we must put a print statement at the end.
def up_down_arrow(a,b):
- return ((a**b) * (b**a))
print(up_down_arrow(up_down_arrow(2,up_down_arrow(1,2)),2))
All those nested up_down_arrow's might be confusing at first, but it really isn't that confusing.
If you run your program, you should get your answer: ![]()
You might be surprised that the answer is so big. If you actually start calculating the real answer without a program, you will really quickly find that the final result is ![]() which does turn out to be 16,777,216 if you use a calculator.
which does turn out to be 16,777,216 if you use a calculator.
Let's make another operation!
We will define the operation ![]() to be called all around.
to be called all around. ![]() That's an operation that will make really big numbers!
That's an operation that will make really big numbers!
Program Example 2
Find 87 all around 132.
The answer is bound to be a huge number, so we must make a program to solve it.
We will keep our up_down_arrow function because in the definition of our all_around function we will use it. Then, we will define the all_around function.
def up_down_arrow(a,b):
- return ((a**b) * (b**a))
def all_around(a,b):
- return ((a * b * up_down_arrow(a,b)) ** 2)
We must print all_around(87,132) at the end. Once we do that, and we run our program, we get a super super huge number that has over 800 digits!
Understanding Functions
Every single function has a return value. If a function does not return anything, the return value is null. Null is a term used in programming as a placeholder that stands for nothing.
Simple Program Example 1
Define a function that adds 1 to an input.
How will the function know what number to add 1 to? We will input a parameter for the function to add 1 to.
def add_one(x):
- return x + 1
In this function, ![]() is the parameter.
is the parameter.
def add_one(x):
- return x + 1
print(add_one(2))
In the print statement, we set ![]() as 2, and the function returns
as 2, and the function returns ![]() so the program prints
so the program prints ![]() .
.
Simple Program Example 2
Define a function that prints out an input.
We will use a parameter again.
def print_function(x):
- print(x)
Uh oh! We have nothing to return! Therefore, we will return nothing (or null), by just writing return.
def print_function(x):
- print(x)
- return
print_function("print_function")
This code prints out print_function. print_function() is said to be called in the final line of the code. Again, we set ![]() , our parameter, as "print_function."
, our parameter, as "print_function."
Flow
Flow consists of if statements, elif (else if) statements, and else statements.
- An if statement checks if a comparison is true.
- An else statement checks if a comparison is not true. It is used after an if statement (and all elif statements after the if statement) and it shares the same comparison as the if statement.
- An elif statement checks for two things: if a comparison is true, and if a comparison is not true. It is used right after the if statement.
Program Example
Does the number 10 have the property that when you multiply 10 by 5, you get a two digit number?
This problem is super easy to solve without a program, but let's write a program to solve this anyway. We will use an if statement to check if ![]() is less than 100 and greater than 9.
is less than 100 and greater than 9.
if 10*5 > 9:
- if 10*5 < 100:
- print("Yes")
- else:
- print("No")
else:
- print("No")
This code means, if 10*5 > 9, then we will check if it is less than 100. If it is not greater than 9, however, we will print No. If it is greater than 9, we check if it is less than 100. If it is, we print Yes. If it isn't we print No.
These nested if statements can be very confusing. Luckily, there is a faster an easier way to do this.
if 10*5 > 9 and 10*5 < 100:
- print("Yes")
else:
- print("No")
This code checks for the two conditions at the same time. If we run it, we get our answer of Yes.
Booleans
Program Example
Print all two digit positive integers ![]() such that
such that ![]() is a two digit positive integer.
is a two digit positive integer.
We can create a function with our previous code.
We will have to slightly modify our function so we can use it in a for loop at the end:
def check(a):
- if a*5 > 9 and a*5 < 100:
- return True
- else:
- return False
True and False are what are called booleans. When an if or elif statement receives True, the code inside of the statement happens. When an if or elif statement receives False, the code inside of the statement does not happen.
We must create a for loop that will iterate through all two digit positive integers.
def check(a):
- if a*5 > 9 and a*5 < 100:
- return True
- else:
- return False
for i in range(10,100):
- if check(i):
- print(i)
The final for loop checks if ![]() is a two digit integer. If it is, the function returns True and the code inside the if statement gets run. If it isn't, the function returns False and the code inside the if statement gets ignored.
is a two digit integer. If it is, the function returns True and the code inside the if statement gets run. If it isn't, the function returns False and the code inside the if statement gets ignored.
If we run this, we will get the answer.
All two digit integers from 10 to 19 inclusive work!
Soft Coding Programs
In the next few examples, you will see why hard coding programs is bad.
Program Example 1
Print all two digit positive integers ![]() such that
such that ![]() is a three digit positive integer.
is a three digit positive integer.
We can keep our code and modify some parts of it.
def check(a, min, max):
- if a*5 > min - 1 and a*5 < max + 1:
- return True
- else:
- return False
def print_check(range_min, range_max, check_min, check_max):
- for i in range(range_min, range_max + 1):
- if check(i, check_min, check_max):
- print(i)
- return
print_check(10, 99, 100, 999)
Why did we add so many functions?
Well, if the numbers in a problem change (and the words stay the same), and you need to change a lot of numbers in your program, your program is considered hard-coded. We want our programs to be as soft-coded as possible. In our new program, we only need to change 4 numbers (in the print_check() statement) if the numbers in the problem change. Therefore, our program is relatively soft-coded. There are still ways to soft-code this program even more, though.
If we run our program, we get our answer.
All numbers from 20 to 99 work!
Program Example 2
Print all three digit positive integers ![]() such that
such that ![]() is a three digit positive integer.
is a three digit positive integer.
We can just change the print_check line at the end to
print_check(100, 999, 100, 999)
and our program will be ready to be run.
All numbers from 100 to 199 work.
Program Example 3
Print all two digit positive integers ![]() such that
such that ![]() is a three digit positive integer.
is a three digit positive integer.
Uh oh. Only changing the print_check line won't work. We will need to change our functions!
def check(a, min, max, factor):
- if a*factor > min - 1 and a*factor < max + 1:
- return True
- else:
- return False
def print_check(range_min, range_max, check_min, check_max, check_factor):
- for i in range(range_min, range_max + 1):
- if check(i, check_min, check_max, check_factor):
- print(i)
- return
print_check(10, 99, 100, 999, 3)
In this step, we added a parameter in both functions. We also soft-coded our program even more! Hooray!
All integers from 34 to 99 work.
Program Example 4
Print all two digit positive integers ![]() such that
such that ![]() is a positive integer from 500 to 900.
is a positive integer from 500 to 900.
This problem may look a bit different from the other ones, but it really is the same thing, except that the factor is 12 and check_min and check_max are 500 and 900, respectively.
Once we change the final print_check line to satisfy our needs, we can run our program.
All numbers from 42 to 75 work!
Congrats! You have written your first programs above 10 lines of code!
Random
There is a package in Python that allows the use of random numbers.
Program Example 1
Generate a random number from 1 to 6.
Easy peasy. We will just generate a random number from 1 to 6 with the package like this:
import random
print(random.randint(1,6))
As you can see, when you run this program, you get a random number from 1 to 6.
Program Example 2
Simulate the rolling of 1000 dice. Now, count the amount of times you roll 6. Print that amount out.
We can create a function that returns a random number from 1 to 6. Then, we can make a for loop that rolls the dice 1000 times and check if it is a 6.
import random
count = 0
def roll():
- return random.randint(1,6)
for i in range(1, 1001):
- if roll() == 6:
- count += 1
print(count)
If we run this, we will get a number around 170.
Program Example 3
Simulate the rolling of 10,000 dice. Now, count the amount of times you roll 3. Print that amount out.
We can keep our roll function and our code inside the for loop, but we need to change our for loop statement.
We can actually soft-code our program more. Let's turn the whole for loop into a function!
import random
def roll():
- return random.randint(1,6)
def count(amount):
- count_ = 0
- for i in range(1, amount+1):
- if roll() == 3:
- count_ += 1
- return count_
print(count(10000))
If we run this code, it works.
Program Example 4
One of my friends loves rolling dice. He is going to roll 1 die tomorrow, 2 dice two days from now, 3 dice three days from now, and so on so that he rolls ![]() dice
dice ![]() days from now. He gets tired rolling dice after rolling dice for 365 days (so the last day he rolls 365 dice). In Python, simulate this. How many times does he roll 3 after 365 days of rolling dice?
days from now. He gets tired rolling dice after rolling dice for 365 days (so the last day he rolls 365 dice). In Python, simulate this. How many times does he roll 3 after 365 days of rolling dice?
We can use a for loop that calls a function multiple times.
import random
def roll():
- return random.randint(1,6)
def count(amount):
- count_ = 0
- for i in range(1, amount+1):
- if roll() == 3:
- count_ += 1
- return count_
total = 0
for i in range(1, 366):
- total += count(i)
print(total)
This is a really long program, but the whole program should make sense if you look at it for a while. We defined our count function in the previous example, and now we are using it with a for loop and a running total.
You should get a number around 11,000 when you run it. Wow, lots of 3's!
Program Example 5
20 of my friends love rolling dice. They are all going to roll 1 die each tomorrow, 2 dice each two days from now, 3 dice each three days from now, and so on so that they roll ![]() dice each
dice each ![]() days from now. But, one of my friends gets tired very quickly and he only rolls dice for 1 day and stops. Another friend only will roll dice for 2 days, and another will roll dice for three days only, and so on up to the fact that my last friend will roll dice for 20 days. In Python, simulate this. How many times does someone roll 3 after everything?
days from now. But, one of my friends gets tired very quickly and he only rolls dice for 1 day and stops. Another friend only will roll dice for 2 days, and another will roll dice for three days only, and so on up to the fact that my last friend will roll dice for 20 days. In Python, simulate this. How many times does someone roll 3 after everything?
We will have to make our for loop into a function again.
import random
def roll():
- return random.randint(1,6)
def count(amount):
- count_ = 0
- for i in range(1, amount+1):
- if roll() == 3:
- count_ += 1
- return count_
def count2(amount)
- total = 0
- for i in range(1, amount + 1):
- total += count(i)
- return total
def count3(amount)
- total = 0
- for i in range(1, amount + 1):
- total += count2(i)
- return total
print(count3(20))
I also made a new function just in case we needed to turn that into a function later.
Make sure you read the code carefully and you fully understand it. If you don't understand every single line of code, then you will get confused later on in this article.
When you run this program, you might be surprised that the answer isn't so big.
Program Example 6
365 of my friends love rolling dice. They are all going to roll 1 die each tomorrow, 2 dice each two days from now, 3 dice each three days from now, and so on so that they roll ![]() dice each
dice each ![]() days from now. But, one of my friends gets tired very quickly and he only rolls dice for 1 day and stops. Another friend only will roll dice for 2 days, and another will roll dice for three days only, and so on up to the fact that my last friend will roll dice for 365 days. In Python, simulate this. How many times does someone roll 3 after everything?
days from now. But, one of my friends gets tired very quickly and he only rolls dice for 1 day and stops. Another friend only will roll dice for 2 days, and another will roll dice for three days only, and so on up to the fact that my last friend will roll dice for 365 days. In Python, simulate this. How many times does someone roll 3 after everything?
Because we soft-coded our program so much, all we have to do is change the last line so the parameter of count3() is 365.
If we run it...we get a big answer, as expected. It also takes quite a while! Our code isn't that efficient, but the program doesn't take WAY TOO LONG, and we are still learning Basic Programming With Python, so we don't have to worry about it now.
You may not have realized that we soft-coded our program at all, but the whole point of functions is so soft-code programs!
Congrats on writing a program that is around 25 lines long!
Very Basic Datatypes
An integer is a basic datatype in Python. Basically, all variables with the datatype of int is an integer.
A string is another basic datatype, and it is a string of characters enclosed by quotes.
Why Are Datatypes So Important?
Let's say we wanted to make a program that would add 2 and 3. Some bogus code would be:
x="2"
y="3"
print(x+y)
If you ran this code, you would get 23. Why is that?
Well, here, x and y are strings. When you perform the addition operator to strings in Python, it concatenates the strings, giving 23.
The real code is:
x=2
y=3
print(x+y)
If you run this, you will get 5, which is correct.
Here's another reason datatypes are important. Now, we will introduce the datatype called the floating point number, or float. A floating point number is a number with a decimal point.
Let's go back to the IDLE. Type "0.1*10". The result is 1.0. Notice the decimal point.
Let's type something different. Type ![]()
WHAT!?
You would have expected the answer to be 1, but it isn't 1. What happened?
Float approximation happened. Most (almost all) programming languages have a bad float approximation. That means that 1.0 can turn into 0.99999999999999 and 0.5 can turn into 0.49999999999999999993. That only happens with floats, so we should try to use floats as sparingly as possible.