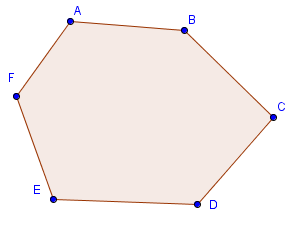
Convex polygon
A convex polygon is a polygon whose interior forms a convex set. That is, if any 2 points on the perimeter of the polygon are connected by a line segment, no point on that segment will be outside the polygon. For example, every regular polygon is convex.
All internal angles of a convex polygon are less than ![]() . Equivalently, all external angles are less than
. Equivalently, all external angles are less than ![]() . The sum of the exterior angles of any convex polygon is
. The sum of the exterior angles of any convex polygon is ![]() and the sum of the internal angles of a convex
and the sum of the internal angles of a convex ![]() -gon is
-gon is ![]() .
.
The convex hull of a finite set of points is a convex polygon with some or all of the points as its vertices.
See also
This article is a stub. Help us out by expanding it.