Difference between revisions of "Cross-Segment Identity"
Mathboy282 (talk | contribs) (Created page with "==Motivation== After repetitive usage of this in AMC/AIME Euclidean Geometry problems, I (mathboy282) only found it fit to make it an identity. ==Identity== Let there be a c...") |
Mathboy282 (talk | contribs) (→Proof) |
||
| Line 14: | Line 14: | ||
| − | [[File:CrossSegment-Identity.png]] | + | [[File:CrossSegment-Identity.png|700px]] |
Latest revision as of 01:35, 2 January 2024
Motivation
After repetitive usage of this in AMC/AIME Euclidean Geometry problems, I (mathboy282) only found it fit to make it an identity.
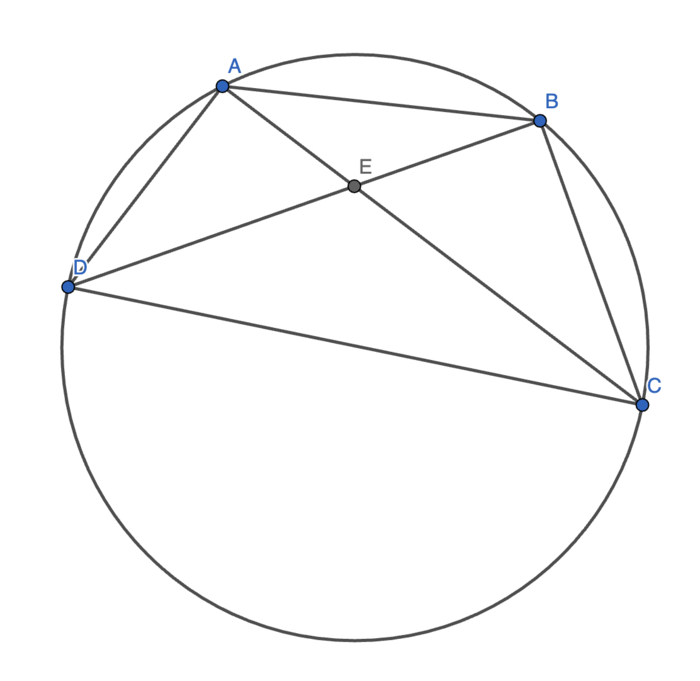
Identity
Let there be a cyclic quadrilateral ![]() with
with ![]() as the intersection of the diagonals
as the intersection of the diagonals ![]() and
and ![]()
Let ![]() and
and ![]() Then, we must have:
Then, we must have:
![]()
Proof
This comes as a direct result of Ptolemy's theorem.
![]()