Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Feuerbach point"

(→‎Sharygin’s prove)
(→‎Sharygin’s prove)
Line 1: Line 1:
 
The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers  and is named after Karl Wilhelm Feuerbach.
 
The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers  and is named after Karl Wilhelm Feuerbach.
−
==Sharygin’s prove==
+
==Sharygin’s proof==
 
<math>1998, 24^{th}</math> Russian math olympiad
 
<math>1998, 24^{th}</math> Russian math olympiad
 
[[File:Feuerbach 1.png|500px|right]]
 
[[File:Feuerbach 1.png|500px|right]]
−
<i><b>Claim 1</b></i>
+
===Claim 1===
−
 
 
 
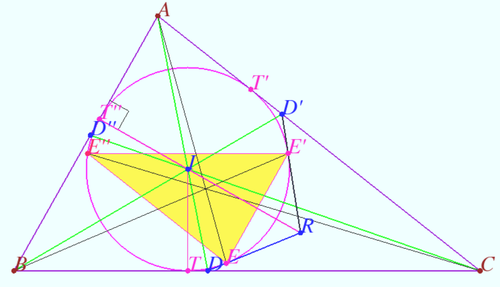
Let <math>D</math> be the base of the bisector of angle A of scalene triangle <math>\triangle ABC.</math>
 
Let <math>D</math> be the base of the bisector of angle A of scalene triangle <math>\triangle ABC.</math>
  
Line 26: Line 25:
 
<math>AE, BE', CE''</math> are concurrent at the homothetic center of <math>\triangle ABC</math> and <math>\triangle EE'E''.</math>
 
<math>AE, BE', CE''</math> are concurrent at the homothetic center of <math>\triangle ABC</math> and <math>\triangle EE'E''.</math>
  
−
<i><b>Claim 2</b></i>
+
===Claim 2===
 
[[File:Feuerbach 2.png|500px|right]]
 
[[File:Feuerbach 2.png|500px|right]]
 
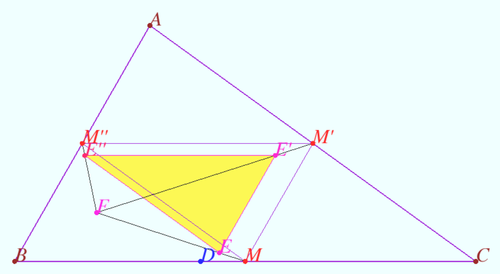
Let <math>M, M',</math> and <math>M''</math> be the midpoints <math>BC, AC,</math> and <math>AB,</math> respectively. Points <math>E, E',</math> and <math>E''</math> was defined at Claim 1.
 
Let <math>M, M',</math> and <math>M''</math> be the midpoints <math>BC, AC,</math> and <math>AB,</math> respectively. Points <math>E, E',</math> and <math>E''</math> was defined at Claim 1.
Line 54: Line 53:
  
 
Therefore <math>MH \cdot MD = MT^2 = ME \cdot MF \implies</math>  points <math>F, E, D,</math> and <math>H</math> are concyclic.
 
Therefore <math>MH \cdot MD = MT^2 = ME \cdot MF \implies</math>  points <math>F, E, D,</math> and <math>H</math> are concyclic.
 +
===Claim 3===
 +
[[File:Feuerbach 3.png|500px|right]]
 +
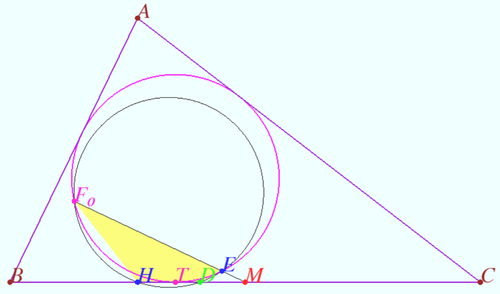
Let <math>H</math> be the base of height <math>AH.</math> Let <math>F_0 = ME \cap \omega \ne E.</math>
 +
Prove that points <math>F_0, E, D,</math> and <math>H</math> are concyclic.
 +
 +
<i><b>Proof</b></i>
 +
 +
<math>MT</math> tangent to <math>\omega \implies MT^2 = ME \cdot MF_0.</math>
 +
Denote <math>a = BC, b = AC, c = AB.</math>
 +
<cmath>BD = \frac {ac}{b+c}, BM = \frac {a}{2} \implies MD = \frac {a(b-c)}{2(b+c)}.</cmath>
 +
<cmath>BT = \frac {a+c-b}{2} \implies MT = \frac {b-c}{2}.</cmath>
 +
Point <math>H</math> lies on radical axis of circles centered at <math>B</math> and <math>C</math> with the radii <math>c</math> and <math>b,</math> respectively. So <math>BH = \frac {a}{2} - \frac {b^2 – c^2}{2a} \implies HM =  \frac {b^2 – c^2}{2a}.</math>
 +
Therefore <math>MH \cdot MD = MT^2 = ME \cdot MF_0 \implies</math> points <math>F_0, E, D,</math> and <math>H</math> are concyclic.

Revision as of 08:32, 29 December 2023

The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers and is named after Karl Wilhelm Feuerbach.

Sharygin’s proof

$1998, 24^{th}$ Russian math olympiad

Feuerbach 1.png

Claim 1

Let $D$ be the base of the bisector of angle A of scalene triangle $\triangle ABC.$

Let $DE$ be a tangent different from side $BC$ to the incircle of $\triangle ABC (E$ is the point of tangency). Similarly, we denote $D', E', D'',$ and $E''.$

Prove that $EE'||AB, \triangle ABC \sim \triangle EE'E'', AE, BE', CE''$ are concurrent.

Proof

Let $T, T',$ and $T''$ be the point of tangency of the incircle $\omega$ and $BC, AC,$ and $AB.$

Let $\angle A = 2 \alpha, \angle B = 2 \beta, \angle C = 2 \gamma, \alpha + \beta + \gamma = 90^\circ.$ WLOG, $\beta > \gamma.$ \[\angle TIT'' = 180^\circ - 2 \beta, \angle ADB = 180^\circ - \alpha - 2 \beta,\] \[\angle DIT = 90^\circ - \angle ADB = \alpha + 2 \beta - 90^\circ = \beta -\gamma, \angle EID = \angle TID \implies\] \[\angle T''IE = \angle T''IT + 2 \angle TID = 180^\circ - 2 \beta + 2(\beta - \gamma) = 180^\circ - 2 \gamma.\] Similarly, $\angle T''IE' = 180^\circ – 2 \gamma \implies$ points $E$ and $E'$ are symmetric with respect $T''I \perp AB \implies AB || EE'.$

Similarly, $BC || E''E', AC || E''E \implies \triangle ABC \sim \triangle EE'E''.$

$AE, BE', CE''$ are concurrent at the homothetic center of $\triangle ABC$ and $\triangle EE'E''.$

Claim 2

Feuerbach 2.png

Let $M, M',$ and $M''$ be the midpoints $BC, AC,$ and $AB,$ respectively. Points $E, E',$ and $E''$ was defined at Claim 1.

Prove that $ME, M'E',$ and $M''E''$ are concurrent.

Proof

\[\triangle ABC \sim \triangle MM'M'' \implies\] \[\triangle MM'M'' \sim \triangle EE'E'' \implies\] $ME, M'E', M''E''$ are concurrent at the homothetic center of $\triangle MM'M''$ and $\triangle EE'E''.$

Claim 3

Feuerbach 3.png

Let $H$ be the base of height $AH.$

Prove that points $F, E, D,$ and $H$ are concyclic.

Proof

$MT$ tangent to $\omega \implies MT^2 = ME \cdot MF.$

Denote $a = BC, b = AC, c = AB.$ \[BD = \frac {ac}{b+c}, BM = \frac {a}{2} \implies MD = \frac {a(b-c)}{2(b+c)}.\] \[BT = \frac {a+c-b}{2} \implies MT = \frac {b-c}{2}.\] Point $H$ lies on radical axis of circles centered at $B$ and $C$ with the radii $c$ and $b,$ respectively. So $BH = \frac {a}{2} - \frac {b^2 - c^2}{2a} \implies HM = \frac {b^2 - c^2}{2a}.$

Therefore $MH \cdot MD = MT^2 = ME \cdot MF \implies$ points $F, E, D,$ and $H$ are concyclic.

Claim 3

Feuerbach 3.png

Let $H$ be the base of height $AH.$ Let $F_0 = ME \cap \omega \ne E.$ Prove that points $F_0, E, D,$ and $H$ are concyclic.

Proof

$MT$ tangent to $\omega \implies MT^2 = ME \cdot MF_0.$ Denote $a = BC, b = AC, c = AB.$ \[BD = \frac {ac}{b+c}, BM = \frac {a}{2} \implies MD = \frac {a(b-c)}{2(b+c)}.\] \[BT = \frac {a+c-b}{2} \implies MT = \frac {b-c}{2}.\] Point $H$ lies on radical axis of circles centered at $B$ and $C$ with the radii $c$ and $b,$ respectively. So $BH = \frac {a}{2} - \frac {b^2 – c^2}{2a} \implies HM = \frac {b^2 – c^2}{2a}.$ Therefore $MH \cdot MD = MT^2 = ME \cdot MF_0 \implies$ points $F_0, E, D,$ and $H$ are concyclic.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Feuerbach_point&oldid=208640"