Kimberling’s point X(24)

Kimberling's point X(24)

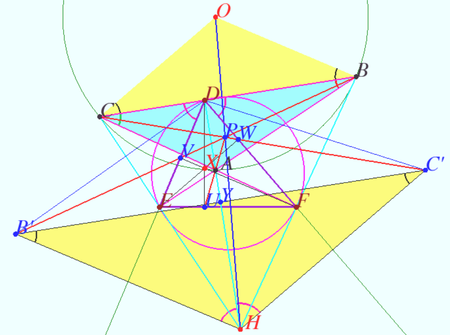
Kimberling defined point X(24) as perspector of $\triangle ABC$ and Orthic Triangle of the Orthic Triangle of $\triangle ABC$ .

Theorem 1

Denote $T_0$ obtuse or acute $\triangle ABC.$ Let $T_0$ be the base triangle, $T_1 = \triangle DEF$ be Orthic triangle of $T_0, T_2 = \triangle UVW$ be Orthic Triangle of the Orthic Triangle of $T_0$ . Let $O$ and $H$ be the circumcenter and orthocenter of $T_0.$

Then $\triangle T_0$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line $OH$ of $T_0.$

The ratio of the homothety is $k = \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

Proof

WLOG, we use case $\angle A = \alpha > 90^\circ.$ Let $B'$ be reflection $H$ in $DE.$

In accordance with Claim, $\angle BVD = \angle HVE \implies B', V,$ and $B$ are collinear.

Similarly, $C, W,$ and $C',$ were $C'$ is reflection $H$ in $DF,$ are collinear.

Denote $\angle ABC = \beta = \angle CHD, \angle ACB = \gamma = \angle BHD \implies$

$\angle HDF = \angle HDE = \angle DHB' = \angle DHC' = 180^\circ - \alpha.$

$B'C' \perp HD, BC \perp HD \implies BC|| B'C'.$ $OB = OC, HB' = HC', \angle BOC = \angle B'HC' = 360^\circ - 2 \alpha \implies OB ||HB', OC || HC' \implies$

$\triangle HB'C' \sim \triangle OBC, BB', CC'$ and $HO$ are concurrent at point $P.$

In accordance with Claim, $\angle HUF = \angle AUF \implies$ points $H$ and $P$ are isogonal conjugate with respect $\triangle UVW.$

$\angle HDE = \alpha - 90^\circ, \angle HCD = 90^\circ - \beta \implies$

$HB' = 2 HD \sin (\alpha - 90^\circ) = - 2 CD \tan(90^\circ- \beta) \cos \alpha = - 2 AC \cos \gamma \frac {\cos \beta}{\sin \beta} \cos \alpha = - 4 OB \cos A \cos B \cos C.$ $k = \frac {HB'}{OB} = \frac {HP}{OP}= - 4 \cos A \cos B \cos C \implies \frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C.$

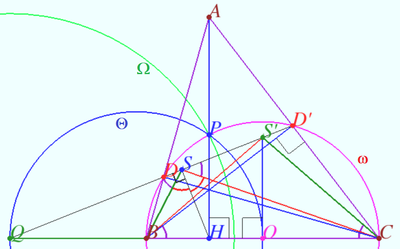
Claim

Let $\triangle ABC$ be an acute triangle, and let $AH, BD',$ and $CD$ denote its altitudes. Lines $DD'$ and $BC$ meet at $Q, HS \perp DD'.$ Prove that $\angle BSH = \angle CSH.$

Proof

Let $\omega$ be the circle $BCD'D$ centered at $O (O$ is midpoint $BC).$

Let $\omega$ meet $AH$ at $P.$ Let $\Omega$ be the circle centered at $Q$ with radius $QP.$

Let $\Theta$ be the circle with diameter $OQ.$

Well known that $AH$ is the polar of point $Q,$ so $QO \cdot HO = QP^2 \implies QB \cdot QC = (QO – R) \cdot (QO + R) = QP^2$ $\implies P \in \Theta, \Omega \perp \omega.$

Let $I_{\Omega}$ be inversion with respect $\Omega, I_{\Omega}(B) = C, I_{\Omega}(H) = O.$

Denote $I_{\Omega}(D) = D', I_{\Omega}(S) = S',$

$HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.$ $\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.$ $\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.$

Theorem 2

Let $T_0 = \triangle ABC$ be the base triangle, $T_1 = \triangle DEF$ be orthic triangle of $T_0, T_2 = \triangle KLM$ be Kosnita triangle. Then $\triangle T_1$ and $\triangle T_2$ are homothetic, the point $P,$ center of this homothety lies on Euler line of $T_0,$ the ratio of the homothety is $k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.$ We recall that vertex of Kosnita triangle are: $K$ is the circumcenter of $\triangle OBC, L$ is the circumcenter of $\triangle OAB, M$ is the circumcenter of $\triangle OAC,$ where $O$ is circumcenter of $T_0.$

vladimir.shelomovskii@gmail.com, vvsss

Page

Toolbox

Search

Kimberling’s point X(24)

Kimberling's point X(24)