Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 7"
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
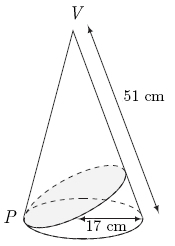
| − | A right circular cone of base radius <math>17</math>cm and slant height <math> | + | A right circular cone of base radius <math>17</math>cm and slant height <math>51</math>cm is given. <math>P</math> is a point on the circumference of the base and the shortest path from <math>P</math> around the cone and back is drawn (see diagram). If the length of this path is <math>m\sqrt{n},</math> where <math>n</math> is squarefree, find <math>m+n.</math> |
[[Image:Mock_AIME_2_2007_Problem8.jpg]] | [[Image:Mock_AIME_2_2007_Problem8.jpg]] | ||
==Solution== | ==Solution== | ||
| − | {{ | + | "Unfolding" this cone results in a circular sector with radius <math>51</math> and arc length <math>17\cdot 2\pi=34\pi</math>. Let the vertex of this sector be <math>O</math>. The problem is then reduced to finding the shortest distance between the two points <math>A</math> and <math>B</math> on the arc that are the farthest away from each other. Since <math>34\pi</math> is <math>1/3</math> of the circumference of a circle with radius <math>51</math>, we must have that <math>\angle AOB=\frac{360^{\circ}}{3}=120^{\circ}</math>. We know that <math>AO=OB=51</math>, so we can use the Law of Cosines to find the length of <math>AB</math>: |
| + | <cmath>AB=\sqrt{AO^2+OB^2-2AO\cdot OB\cdot\cos{120^{\circ}}}=\sqrt{51^2+51^2+51^2}=51\sqrt{3}.</cmath> | ||
| + | Hence <math>m=51</math>, <math>n=3</math>, <math>m+n=\boxed{054}</math>. | ||
| − | + | ==See Also== | |
| − | + | {{Mock AIME box|year=2006-2007|n=2|num-b=6|num-a=8}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
Latest revision as of 18:10, 10 July 2014
Problem
A right circular cone of base radius ![]() cm and slant height
cm and slant height ![]() cm is given.
cm is given. ![]() is a point on the circumference of the base and the shortest path from
is a point on the circumference of the base and the shortest path from ![]() around the cone and back is drawn (see diagram). If the length of this path is
around the cone and back is drawn (see diagram). If the length of this path is ![]() where
where ![]() is squarefree, find
is squarefree, find ![]()
Solution
"Unfolding" this cone results in a circular sector with radius ![]() and arc length
and arc length ![]() . Let the vertex of this sector be
. Let the vertex of this sector be ![]() . The problem is then reduced to finding the shortest distance between the two points
. The problem is then reduced to finding the shortest distance between the two points ![]() and
and ![]() on the arc that are the farthest away from each other. Since
on the arc that are the farthest away from each other. Since ![]() is
is ![]() of the circumference of a circle with radius
of the circumference of a circle with radius ![]() , we must have that
, we must have that ![]() . We know that
. We know that ![]() , so we can use the Law of Cosines to find the length of
, so we can use the Law of Cosines to find the length of ![]() :
:
![]() Hence
Hence ![]() ,
, ![]() ,
, ![]() .
.
See Also
| Mock AIME 2 2006-2007 (Problems, Source) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||