Difference between revisions of "Mock AIME 2 2006-2007 Problems/Problem 7"
| Line 1: | Line 1: | ||
| − | + | == Problem == | |
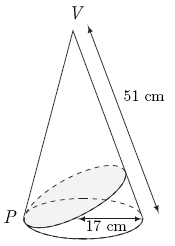
| − | [[Image: | + | A right circular cone of base radius <math>\displaystyle 17</math>cm and slant height <math>\displaystyle 34</math>cm is given. <math>\displaystyle P</math> is a point on the circumference of the base and the shortest path from <math>\displaystyle P</math> around the cone and back is drawn (see diagram). If the length of this path is <math>\displaystyle m\sqrt{n},</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers, find <math>\displaystyle m+n.</math> |
| + | |||
| + | [[Image:Mock_AIME_2_2007_Problem8.jpg]] | ||