Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Simson line"

(→‎Simson line (main))
(→‎Simson line (main))
Line 6: Line 6:
 
==Simson line (main)==
 
==Simson line (main)==
 
[[File:Simson line.png|300px|right]]
 
[[File:Simson line.png|300px|right]]
−
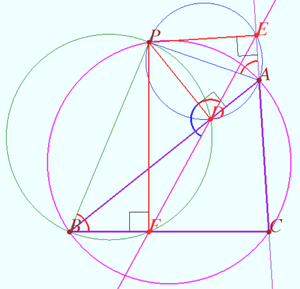
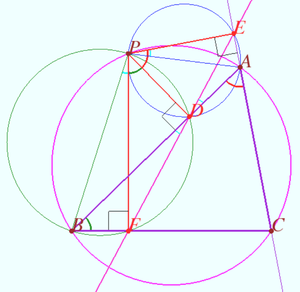
Let a triangle <math>\triangle ABC</math> and a point <math>P</math> be given. Let <math>D, E,</math> and <math>F</math> be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.
+
[[File:Simson line inverse.png|300px|right]]
 +
Let a triangle <math>\triangle ABC</math> and a point <math>P</math> be given.
 +
 
 +
Let <math>D, E,</math> and <math>F</math> be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.
  
 
Then points  <math>D, E,</math> and <math>F</math> are collinear iff the point <math>P</math> lies on circumcircle of <math>\triangle ABC.</math>
 
Then points  <math>D, E,</math> and <math>F</math> are collinear iff the point <math>P</math> lies on circumcircle of <math>\triangle ABC.</math>
Line 29: Line 32:
  
 
Let the points  <math>D, E,</math> and <math>F</math> be collinear.  
 
Let the points  <math>D, E,</math> and <math>F</math> be collinear.  
−
[[File:Simson line inverse.png|300px|right]]
+
 
 
<math>AEPD</math> is cyclic <math>\implies \angle APE = \angle ADE, \angle APE = \angle BAC.</math>  
 
<math>AEPD</math> is cyclic <math>\implies \angle APE = \angle ADE, \angle APE = \angle BAC.</math>  
  
Line 39: Line 42:
  
 
<math>ACBP</math> is cyclis as desired.
 
<math>ACBP</math> is cyclis as desired.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
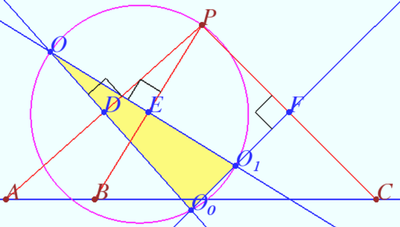
==Problem==
 +
[[File:Problem on Simson line.png |400px|right]]
 +
 +
Let the points <math>A, B,</math> and <math>C</math> be collinear and the point <math>P \notin AB.</math>
 +
 +
Let <math>O,O_0,</math> and <math>O_1</math> be the circumcenters of triangles <math>\triangle ABP, \triangle ACP,</math> and <math>\triangle BCP.</math>
 +
 +
Prove that <math>P</math> lies on circumcircle of <math>\triangle OO_0O_1.</math>
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>D, E,</math> and <math>F</math> be the midpoints of segments <math>AB, AC,</math> and <math>BC,</math> respectively.
 +
 +
Then points  <math>D, E,</math> and <math>F</math> are collinear <math>(DE||AB, EF||DC).</math>
 +
 +
<math>PD \perp OO_0, PE \perp OO_1, PF \perp O_0O_1 \implies</math>
 +
<math>DEF</math> is Simson line of <math>\triangle OO_0O_1 \implies P</math> lies on circumcircle of <math>\triangle OO_0O_1</math> as desired.
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 15:55, 30 November 2022

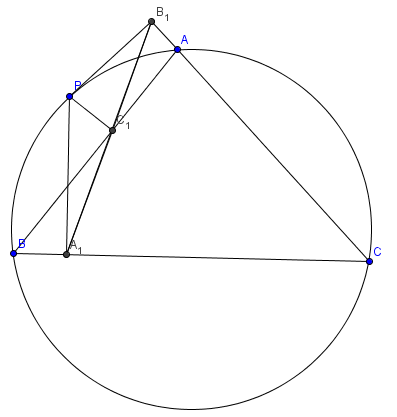
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. Simsonline.png

Proof

In the shown diagram, we draw additional lines $AP$ and $BP$. Then, we have cyclic quadrilaterals $ACBP$, $PC_1A_1B$, and $PB_1AC_1$. (more will be added)

Simson line (main)

Simson line.png
Simson line inverse.png

Let a triangle $\triangle ABC$ and a point $P$ be given.

Let $D, E,$ and $F$ be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.

Then points $D, E,$ and $F$ are collinear iff the point $P$ lies on circumcircle of $\triangle ABC.$

Proof

Let the point $P$ be on the circumcircle of $\triangle ABC.$

$\angle BFP = \angle BDP = 90^\circ \implies$

$BPDF$ is cyclic $\implies \angle PDF = 180^\circ – \angle CBP.$

$\angle ADP = \angle AEP = 90^\circ \implies$

$AEPD$ is cyclic $\implies \angle PDE = \angle PAE.$

$ACBP$ is cyclic $\implies \angle PBC = \angle PAE \implies \angle PDF + \angle PDE = 180^\circ$

$\implies D, E,$ and $F$ are collinear as desired.

Proof

Let the points $D, E,$ and $F$ be collinear.

$AEPD$ is cyclic $\implies \angle APE = \angle ADE, \angle APE = \angle BAC.$

$BFDP$ is cyclic $\implies \angle BPF = \angle BDF, \angle DPF = \angle ABC.$

$\angle ADE = \angle BDF \implies \angle BPA = \angle EPF$

$= \angle BAC + \angle ABC = 180^\circ – \angle ACB \implies$

$ACBP$ is cyclis as desired.

vladimir.shelomovskii@gmail.com, vvsss

Problem

Problem on Simson line.png

Let the points $A, B,$ and $C$ be collinear and the point $P \notin AB.$

Let $O,O_0,$ and $O_1$ be the circumcenters of triangles $\triangle ABP, \triangle ACP,$ and $\triangle BCP.$

Prove that $P$ lies on circumcircle of $\triangle OO_0O_1.$

Proof

Let $D, E,$ and $F$ be the midpoints of segments $AB, AC,$ and $BC,$ respectively.

Then points $D, E,$ and $F$ are collinear $(DE||AB, EF||DC).$

$PD \perp OO_0, PE \perp OO_1, PF \perp O_0O_1 \implies$ $DEF$ is Simson line of $\triangle OO_0O_1 \implies P$ lies on circumcircle of $\triangle OO_0O_1$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Simson_line&oldid=183352"