Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Steiner line"

(→‎Collings Clime)
(→‎Collings Clime)
Line 23: Line 23:
  
 
Similarly <math>\angle CH_BE = \angle CHE = \angle CH_A \implies CH_BH_AP</math> is cyclic <math>\implies P \in \Omega \implies</math> the crosspoint of  <math>l_B</math> and <math>l_A</math> is point <math>P.</math>
 
Similarly <math>\angle CH_BE = \angle CHE = \angle CH_A \implies CH_BH_AP</math> is cyclic <math>\implies P \in \Omega \implies</math> the crosspoint of  <math>l_B</math> and <math>l_A</math> is point <math>P.</math>
 +
 +
Usually the point <math>P</math> is called the anti-Steiner point of the <math>H-line</math> with respect to <math>\triangle ABC.</math>
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 11:58, 7 December 2022

Steiner line

Let $ABC$ be a triangle with orthocenter $H. S$ is a point on the circumcircle $\Omega$ of $\triangle ABC.$ Then, the reflections of $S$ in three edges $BC, CA, AB$ and point $H$ lie on a line $s$ which is known as the Steiner line of point $S$ with respect to $\triangle ABC.$

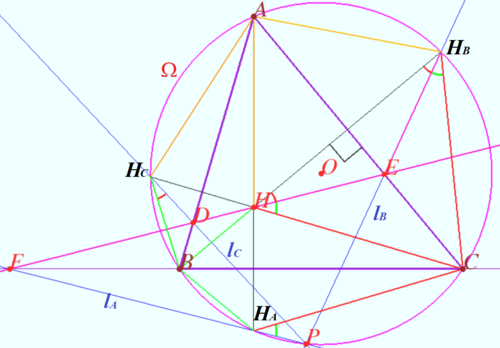
Collings Clime

Steiner H line.png

Let triangle $ABC$ be the triangle with the orthocenter $H$ and circumcircle $\Omega.$ Denote $H–line$ any line containing point $H.$

Let $l_A, l_B,$ and $l_C$ be the reflections of $H-line$ in the edges $BC, AC,$ and $AB,$ respectively.

Prove that lines $l_A, l_B,$ and $l_C$ are concurrent and the point of concurrence lies on $\Omega.$

Proof

Let $D, E,$ and $F$ be the crosspoints of $H–line$ with $AB, AC,$ and $BC,$ respectively.

WLOG $D \in AB, E \in AC.$ Let $H_A, H_B,$ and $H_C$ be the points symmetric to $H$ with respect $BC, AC,$ and $AB,$ respectively.

Therefore $H_A \in l_A, H_B \in l_B, H_C \in l_C,$ \[AH = AH_B = AH_C, BH = BH_A = BH_C, CH = CH_A = CH_B \implies\] \[\angle HH_BE = \angle EHH_B = \angle BHD = \angle BH_CD.\]

Let $P$ be the crosspoint of $l_B$ and $l_C \implies BH_CH_BP$ is cyclic $\implies P \in \Omega.$

Similarly $\angle CH_BE = \angle CHE = \angle CH_A \implies CH_BH_AP$ is cyclic $\implies P \in \Omega \implies$ the crosspoint of $l_B$ and $l_A$ is point $P.$

Usually the point $P$ is called the anti-Steiner point of the $H-line$ with respect to $\triangle ABC.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Steiner_line&oldid=183702"