Steiner line
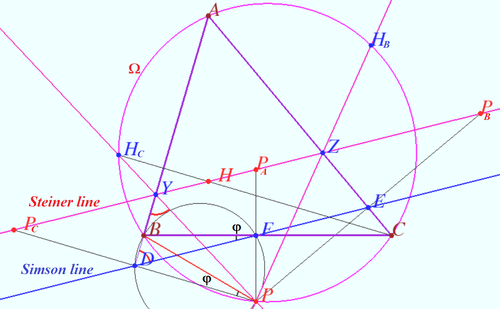
Steiner line
Let ![]() be a triangle with orthocenter
be a triangle with orthocenter ![]() is a point on the circumcircle
is a point on the circumcircle ![]() of
of ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in three lines which contains edges
in three lines which contains edges ![]() and
and ![]() respectively.
respectively.
Prove that ![]() and
and ![]() are collinear. Respective line is known as the Steiner line of point
are collinear. Respective line is known as the Steiner line of point ![]() with respect to
with respect to ![]()
Proof
Let ![]() and
and ![]() be the foots of the perpendiculars dropped from
be the foots of the perpendiculars dropped from ![]() to lines
to lines ![]() and
and ![]() respectively.
respectively.
WLOG, Steiner line cross ![]() at
at ![]() and
and ![]() at
at ![]()
The line ![]() is Simson line of point
is Simson line of point ![]() with respect of
with respect of ![]()
![]() is midpoint of segment
is midpoint of segment ![]() homothety centered at
homothety centered at ![]() with ratio
with ratio ![]() sends point
sends point ![]() to a point
to a point ![]()
Similarly, this homothety sends point ![]() to a point
to a point ![]() , point
, point ![]() to a point
to a point ![]() therefore this homothety send Simson line to line
therefore this homothety send Simson line to line ![]()
Let ![]()
![]()
![]() is simmetric to
is simmetric to ![]()
Quadrungle ![]() is cyclic
is cyclic ![]()
![]() at point
at point ![]() Similarly, line
Similarly, line ![]() at
at ![]()
According the Collins Claim ![]() is
is ![]() therefore
therefore ![]()
vladimir.shelomovskii@gmail.com, vvsss
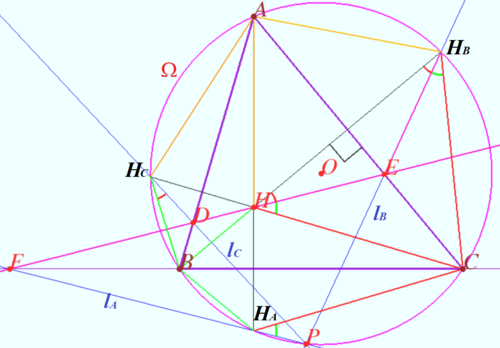
Collings Clime
Let triangle ![]() be the triangle with the orthocenter
be the triangle with the orthocenter ![]() and circumcircle
and circumcircle ![]() Denote
Denote ![]() any line containing point
any line containing point ![]()
Let ![]() and
and ![]() be the reflections of
be the reflections of ![]() in the edges
in the edges ![]() and
and ![]() respectively.
respectively.
Prove that lines ![]() and
and ![]() are concurrent and the point of concurrence lies on
are concurrent and the point of concurrence lies on ![]()
Proof
Let ![]() and
and ![]() be the crosspoints of
be the crosspoints of ![]() with
with ![]() and
and ![]() respectively.
respectively.
WLOG ![]() Let
Let ![]() and
and ![]() be the points symmetric to
be the points symmetric to ![]() with respect
with respect ![]() and
and ![]() respectively.
respectively.
Therefore ![]()
![]()
![]()
Let ![]() be the crosspoint of
be the crosspoint of ![]() and
and ![]() is cyclic
is cyclic ![]()
Similarly ![]() is cyclic
is cyclic ![]() the crosspoint of
the crosspoint of ![]() and
and ![]() is point
is point ![]()
Usually the point ![]() is called the anti-Steiner point of the
is called the anti-Steiner point of the ![]() with respect to
with respect to ![]()
vladimir.shelomovskii@gmail.com, vvsss
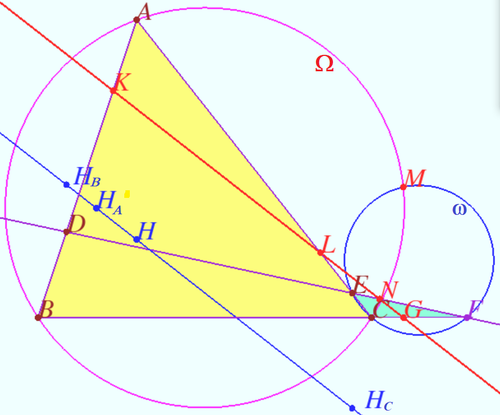
Ortholine
Let four lines made four triangles of a complete quadrilateral.
In the diagram these are ![]()
Let points ![]() and
and ![]() be the orthocenters of
be the orthocenters of ![]() and
and ![]() respectively.
respectively.
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
Let ![]() be Miquel point of a complete quadrilateral.
be Miquel point of a complete quadrilateral.
Line ![]() is the line which contain
is the line which contain ![]() Simson lines of
Simson lines of ![]() triangles.
triangles.
Using homothety centered at ![]() with ratio
with ratio ![]() we get
we get ![]() coinciding Stainer lines which contain points
coinciding Stainer lines which contain points ![]() and
and ![]() .
.
vladimir.shelomovskii@gmail.com, vvsss