Math history is full of incredible thinkers, innovators, and personalities. One of these talents was Italian mathematician Giovanni Ceva! Ceva is most known for his eponymous theorem and we have a challenge for you: try your hand at proving Ceva's Theorem. Then, after attempting the theorem yourself, read on to find the solution.
Ceva's Theorem
Draw any triangle and pick any point inside the triangle. Next, draw segments from each vertex through the chosen point to the opposite side. Then, the product of the red lengths below will always equal the product of the blue lengths below.
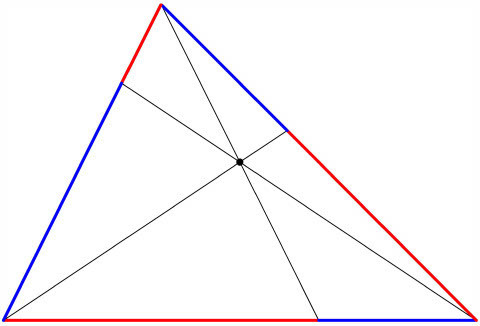
Can you walk in Ceva's shoes and prove that it always works?
How Can You Prove Ceva's Theorem?
Here's one way.
First, let's label the red distances p, q, r and the blue distances x, y, z as shown below:
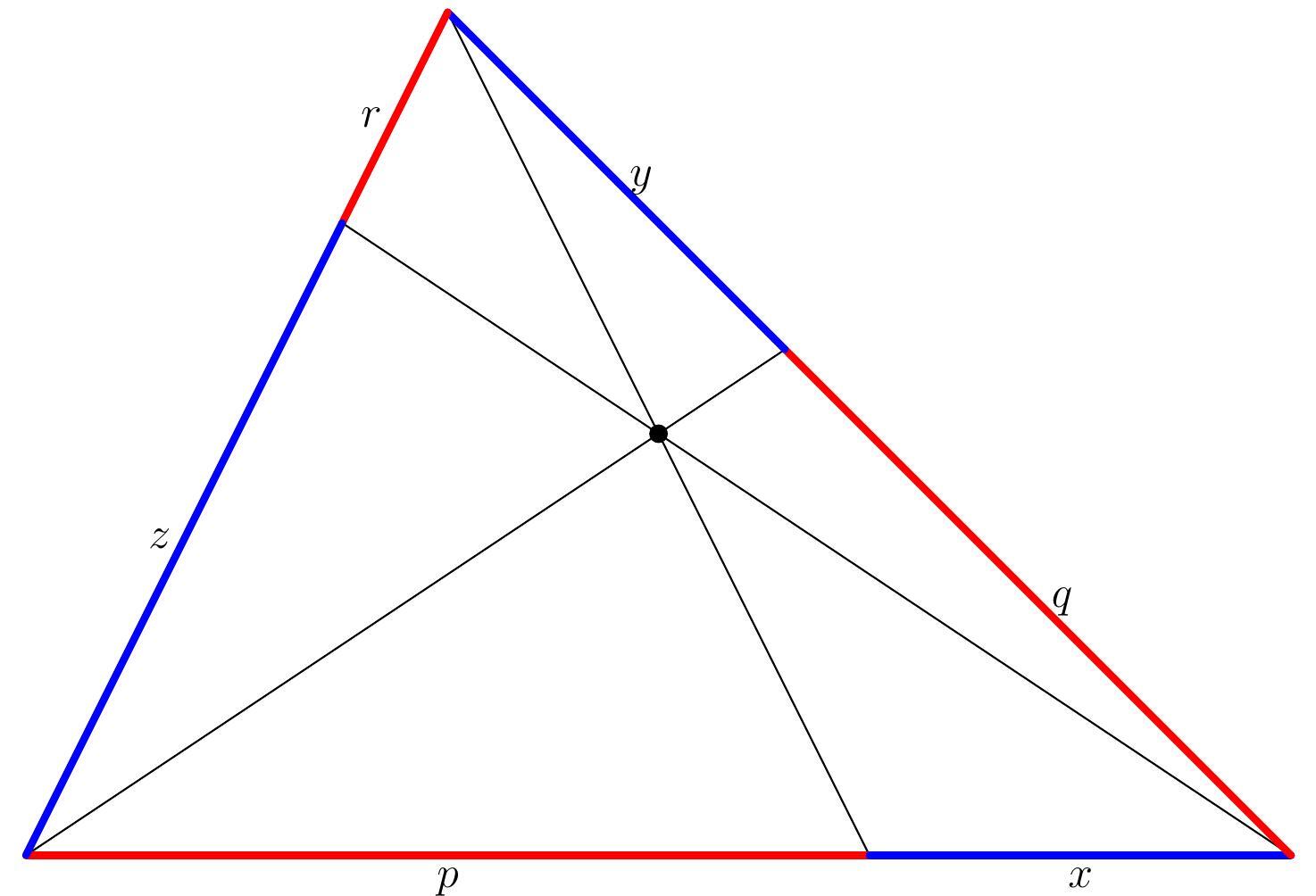
Consider the red and blue shaded triangles in the picture below:
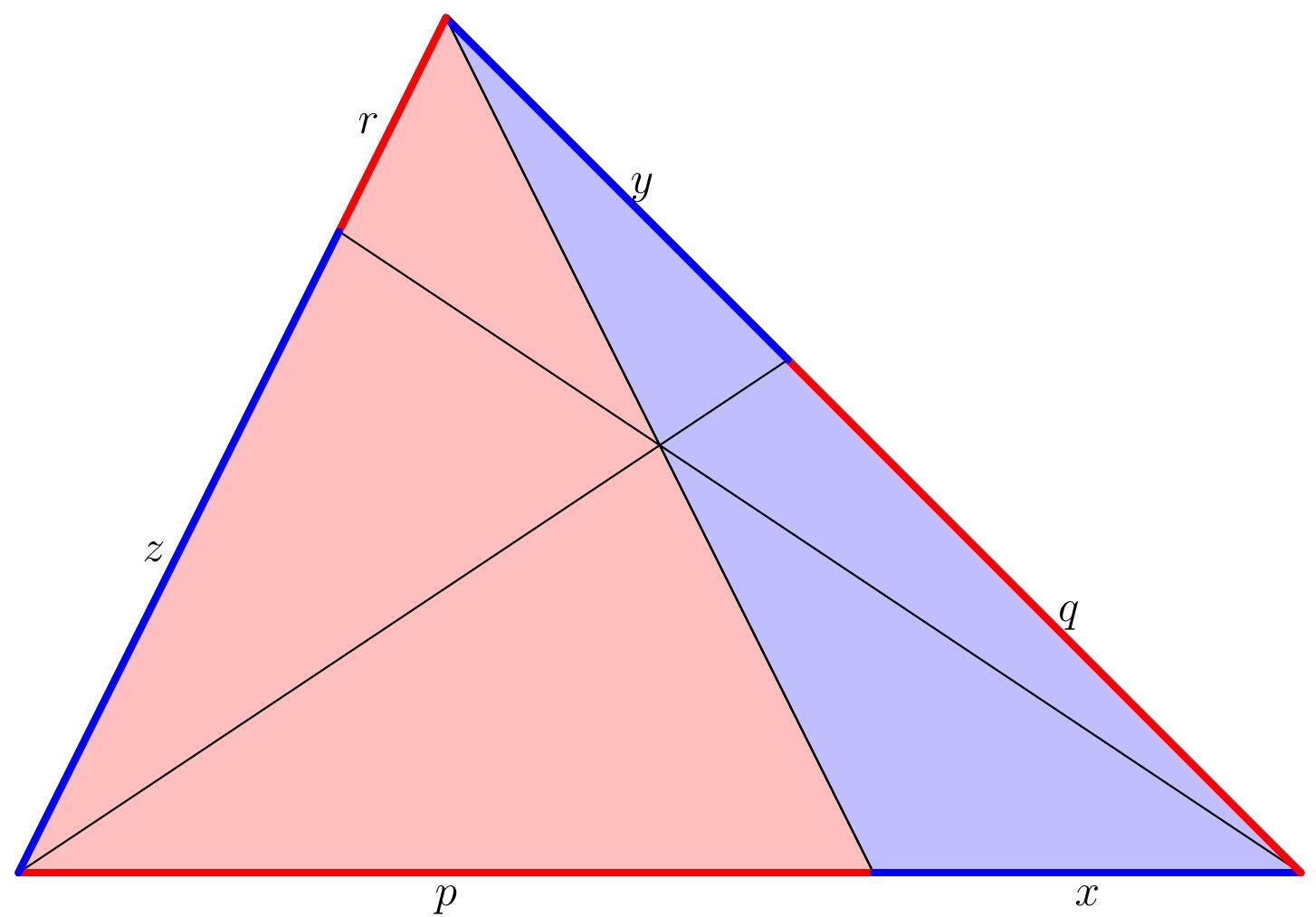
They have the same height, but the red triangle has base p and the blue triangle has base x. Therefore:
But we can also do the same thing with the smaller shaded triangles in the picture below:
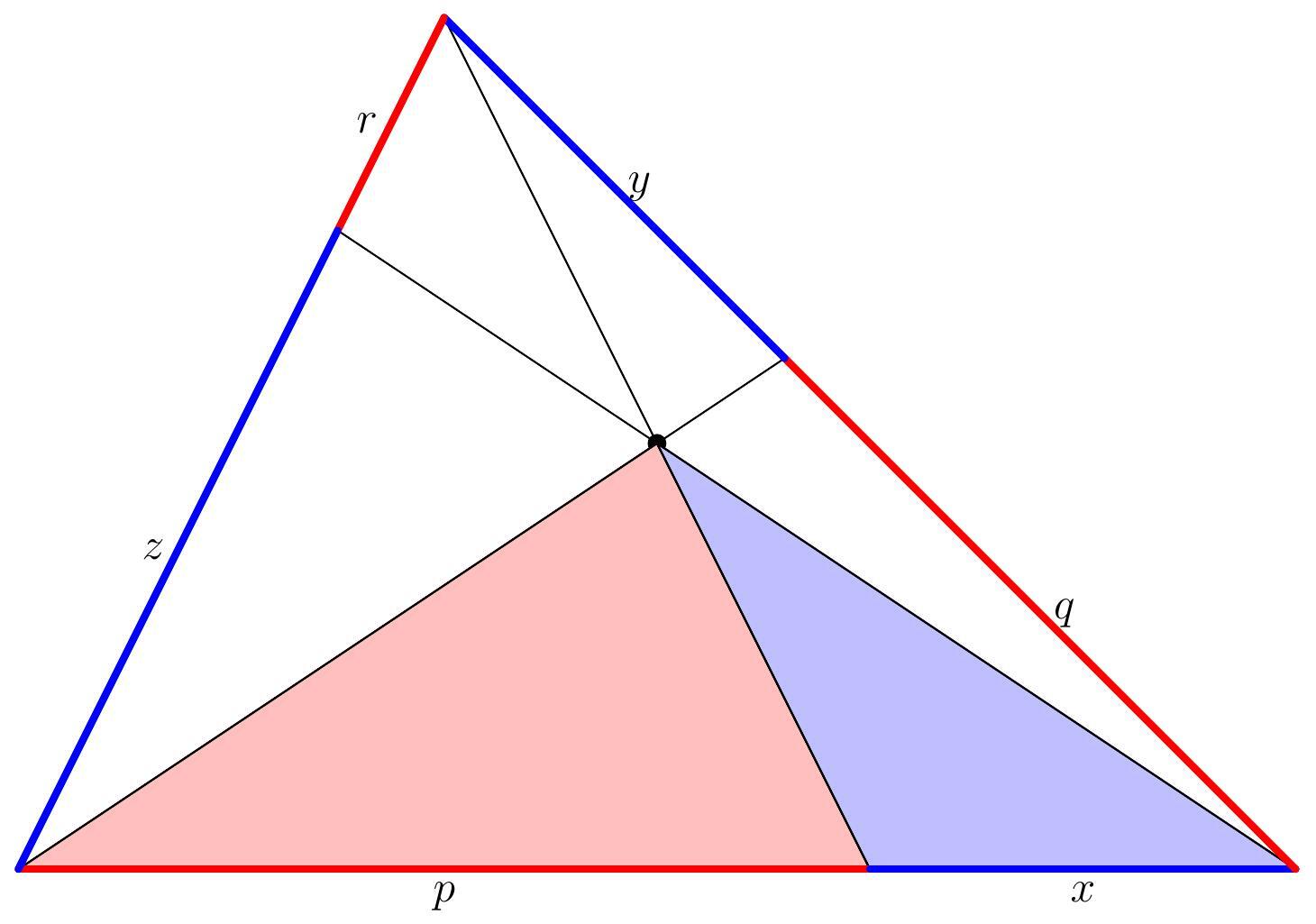
These two triangles also have the same height but different bases. Again, we get
When we take the difference, we get the yellow and green triangles below:
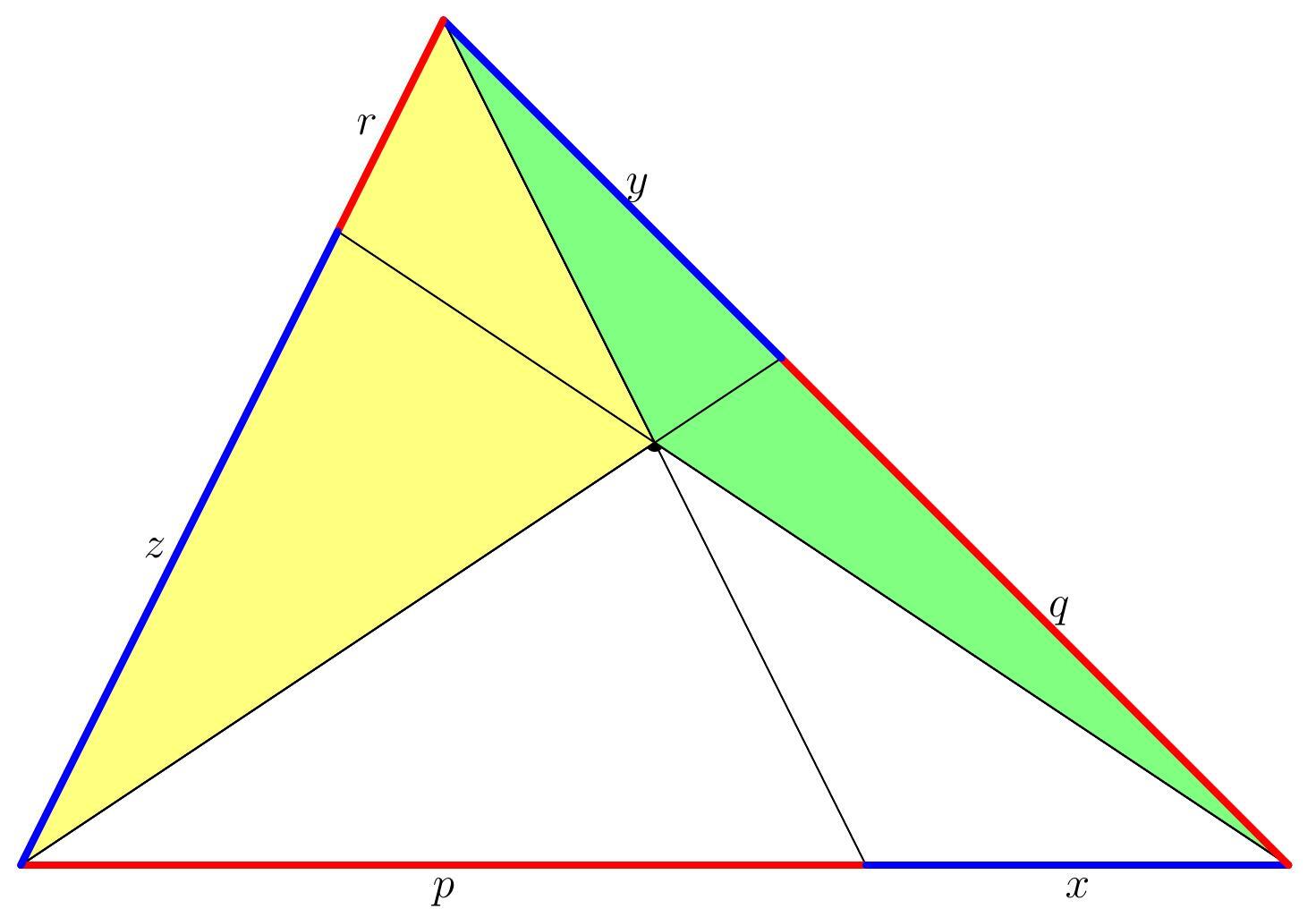
These new triangles still have the same ratio of areas:
Now, let's use purple to shade the rest of the triangle, and do the same calculation using the other two sides of the big triangle.
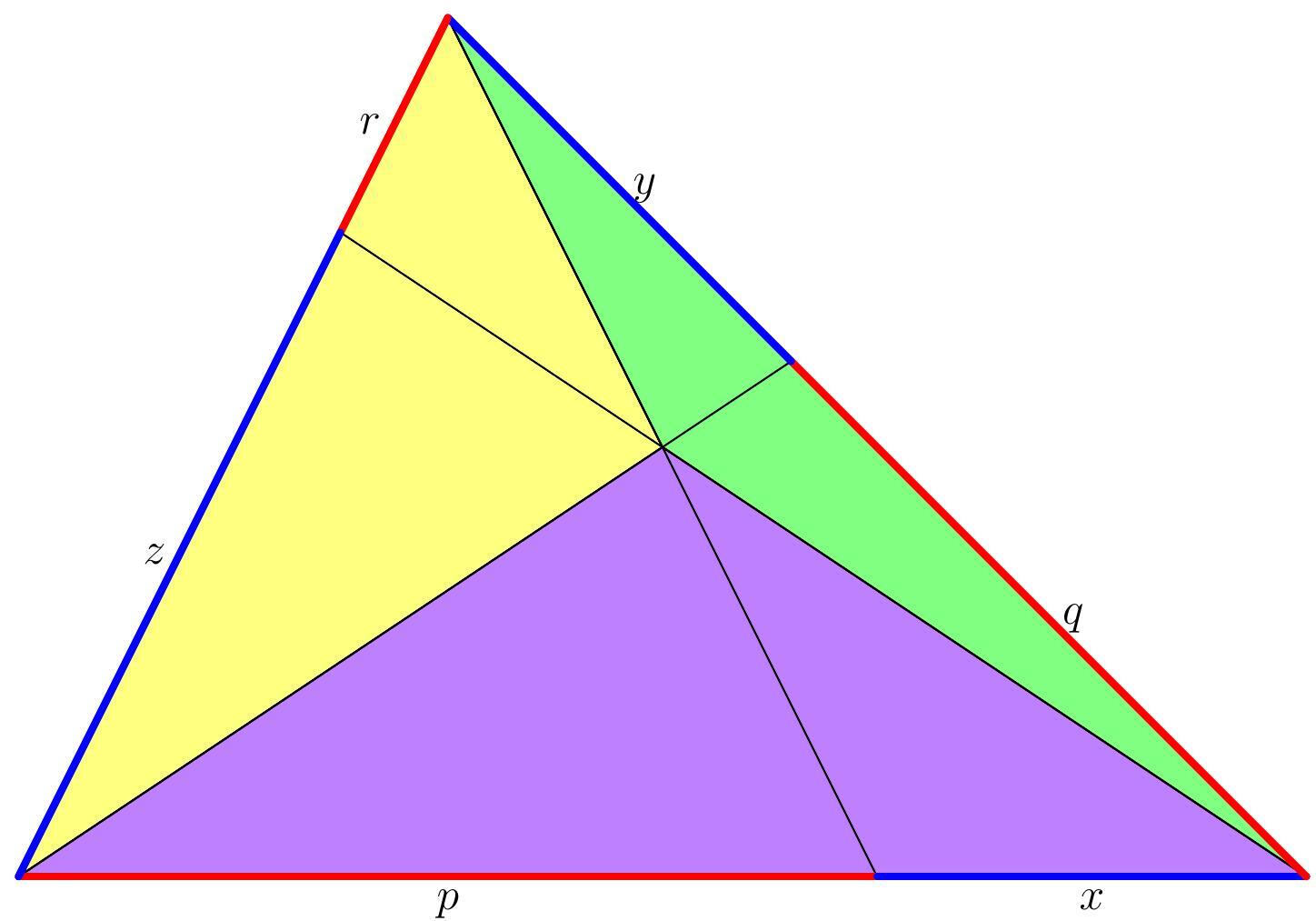
We get
What Happens When We Multiply These All Together?
All of the areas on the left sides of these equations cancel out! (Each area appears in one numerator and one denominator.)
So, we're left with:
This simplifies to xyz = pqr, which is exactly what Ceva's Theorem states.
And we're done!











