Math Jams

rrusczyk 2010-09-22 19:21:39
Hello. This is the Math Jam classroom. The Math Jam will start at 7:30 PM ET (4:30 PM PT).

rrusczyk 2010-09-22 19:23:12
This is not the classroom for Intermediate Counting & Probability, Introduction to Geometry, MATHCOUNTS/AMC 8 Basics, or Intro to Programming. This is the AoPS Classes Math Jam. If you are enrolled in a course and trying to attend it, then you should leave the classroom now, click Classroom, and then choose the appropriate link on the next page.

rrusczyk 2010-09-22 19:25:00
The classroom is moderated: students can type into the classroom, but only the moderators can choose a comment to drop into the classroom. So, when you send a message, it will not appear immediately, and may not appear at all.

rrusczyk 2010-09-22 19:30:14
We'll be getting started in just a minute.

rrusczyk 2010-09-22 19:32:18
Let's get started!

rrusczyk 2010-09-22 19:32:30
Hello, and welcome to an Art of Problem Solving Math Jam. Today we'll be discussing Art of Problem Solving classes. We'll start with a few sample problems, so you can get a little taste of what the classes are like. Then, I'll give an overview of how our courses work, and answer any questions you may have about the courses.

rrusczyk 2010-09-22 19:32:35
My name is Richard Rusczyk. I founded Art of Problem Solving and have written several Art of Problem Solving textbooks.

rrusczyk 2010-09-22 19:32:42
Before we get started I would like to take a moment to explain our Virtual Classroom to those who have not previously participated in a Math Jam or one of our online classes.

rrusczyk 2010-09-22 19:32:52
The classroom is moderated: students can type into the classroom, but only the moderators can choose a comment to drop into the classroom. So, when you send a message, it will not appear immediately, and may not appear at all. This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read. Also, only moderators can enter into private chats with other people in the classroom.

rrusczyk 2010-09-22 19:33:22
In general in our classes, we have assistant instructors in all of our classes, and all math questions get answered by the primary instructor of the assistants. Tonight, since there are so many of you, we might not be able to answer *every single math question*, but we get to them all in the classes.

rrusczyk 2010-09-22 19:33:39
As for questions about the classes, we will try to answer all of those tonight. I will let you know when to start asking questions about specific classes.

rrusczyk 2010-09-22 19:33:47
Also, note that you can adjust the sizing of the classroom to your liking; feel free to experiment with it!

rrusczyk 2010-09-22 19:34:18
In this Math Jam, we will start off by doing a few sample problems. These will be drawn from our Introduction to Number Theory and Introduction to Counting & Probability courses. We won't be doing problems from all of the courses tonight, since that would take too long. Instead, we'll just do a batch of problems at the beginning of the Math Jam, and discuss the courses for the remainder of the class.

rrusczyk 2010-09-22 19:34:35
If you're just here to discuss the courses, you can tune out for 15-20 minutes while we do some math. You can also read more about how our courses work here:

rrusczyk 2010-09-22 19:34:39
http://www.artofproblemsolving.com/School/index.php?page=classinformation

rrusczyk 2010-09-22 19:34:44
And you can read more about our online classroom here:

rrusczyk 2010-09-22 19:34:49
http://www.artofproblemsolving.com/School/index.php?page=howclassroomworks

rrusczyk 2010-09-22 19:35:09
Before we get started, I'd like to note that the mathematics we will discuss today covers a *very* wide range of difficulty. Moreover, I know that many of you are here just to check out the classroom before your classes start.

rrusczyk 2010-09-22 19:35:22
Please understand that if you are enrolled in one of our introductory classes, or haven't much experience yet with advanced problem solving, then much of the material we cover tonight might be well beyond you right now. We won't be able to teach you all the math you need to understand this material in one night! So, don't be frustrated if you don't understand the problems we discuss for those classes -- your time will come!

rrusczyk 2010-09-22 19:35:43
Our assisting tonight is Ariana Levin; her username is ArianaL.

rrusczyk 2010-09-22 19:35:54
Ariana discovered AoPS after participating in the first Math Prize for Girls competition. Ariana promoted math in high school as a member of the Mu Alpha Theta National Honor Society. She also pole-vaulted on the track and field team, because pole vault was the only event that enables flight by a double pendulum. Ariana is entering the Women in Science and Engineering (WiSE) program at Stony Brook University in the fall. She plans to double major in math and biology

rrusczyk 2010-09-22 19:36:09
She'll be answering some of your questions. Sometimes she'll do so by whispering to you, other times she'll do so by opening a private window with you.

rrusczyk 2010-09-22 19:36:21
One quick note before we start on the math. While the discussion tonight will be similar to that in our classes, there are a few differences between tonight and the typical class.

rrusczyk 2010-09-22 19:36:37
There is a much wider range of students here tonight than in our typical classes. So, some of you will find tonight's material very, very easy, and others will find it very, very hard. Also, because there's such a wide spread of students, we typically end up going a bit faster in the Math Jam than we do in class.

rrusczyk 2010-09-22 19:36:56
Furthermore, there are more students here tonight than in a typical class. In our classes, we get to all the student questions, and everyone who is participating gets lots of "air time" in the classroom. We also often have an extra assistant in our usual classes.

rrusczyk 2010-09-22 19:37:06
Now, let's do a few problems, and then we'll discuss the courses.

rrusczyk 2010-09-22 19:37:24
Here comes the first problem:

rrusczyk 2010-09-22 19:37:25
Suppose we have a group of 4 girls and 3 boys and we wish to seat them in a row of 7 chairs. In how many ways can the students be seated?

rrusczyk 2010-09-22 19:37:34
Note that I can stick the problem to the top of the classroom, so it won't scroll away while we discuss it; you can adjust the bar between it and the rest of the room.

2012 2010-09-22 19:37:44
Are the students distinguishable?

iwinforthewin 2010-09-22 19:37:45
are the boys and girls distinguishable?

rrusczyk 2010-09-22 19:37:50
No twins here!

rrusczyk 2010-09-22 19:37:57
They're all different

ln25e6 2010-09-22 19:38:10
7!

load 2010-09-22 19:38:10
7!

bulutcocuk 2010-09-22 19:38:10

rrusczyk 2010-09-22 19:38:19
Um, what's that exclamation point all about?

number.sense 2010-09-22 19:38:35
factorial

catlover114 2010-09-22 19:38:35
factorial

$LaTeX$ 2010-09-22 19:38:35
*factorial

2012 2010-09-22 19:38:35
Factorial

Orange-2728 2010-09-22 19:38:35
7 factorial

Qazmaz 2010-09-22 19:38:35
factorials

mackamom 2010-09-22 19:38:35
factoral

Caphi100 2010-09-22 19:38:35
itt means factorial

rrusczyk 2010-09-22 19:38:38
What's that?

harukikara 2010-09-22 19:38:53
7! = 7x6x5x4x3x2x1

iwinforthewin 2010-09-22 19:38:53
7! means 7 factorial, or 7x6x5x...x2x1

kevin7 2010-09-22 19:38:58
7! = 7*6*5*4*3*2*1

joyofpi 2010-09-22 19:38:58
n!=1x2x3x...n

mackamom 2010-09-22 19:38:58
7*6*5*4*3*2*1

number.sense 2010-09-22 19:39:00
multiply all numbers from 1 to the number

rrusczyk 2010-09-22 19:39:04
Exactly.

2012 2010-09-22 19:39:17
We can count the possibilities for the first, and then the second, and the third, etc...

rrusczyk 2010-09-22 19:39:19
This problem is a straightforward application of multiplication: there are 7 students who could sit in the first seat. For each of these choices we make for the first seat, there are six ways to choose a student for the next seat, so there are 7 x 6 ways to seat the first two students.

rrusczyk 2010-09-22 19:39:25
Continuing in this vein, for each of these 7 x 6 ways to seat the first two students, there are 5 ways to pick a student for the third seat. Thus, there are 7 x 6 x 5 ways to seat the first three students.

number.sense 2010-09-22 19:39:31
because there are 7 ways to seat first one 6 to seat second and so on

rrusczyk 2010-09-22 19:39:34
We keep going like this: there are 4 ways to seat the fourth student, 3 ways to seat the fifth, 2 ways to seat the sixth, and one way to seat the last student. This gives us 7 x 6 x 5 x 4 x 3 x 2 x 1 ways to seat all the students.

rrusczyk 2010-09-22 19:39:40
We run into products like 7 x 6 x 5 x 4 x 3 x 2 x 1 so much in mathematics that we have a symbol and a name for it. We write 7 x 6 x 5 x 4 x 3 x 2 x 1 = 7! and we call this 'seven factorial'.

rrusczyk 2010-09-22 19:39:45
Similarly,

rrusczyk 2010-09-22 19:39:50
6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.

$LaTeX$ 2010-09-22 19:40:01
7!=5040

number.sense 2010-09-22 19:40:01
5040

Orange-2728 2010-09-22 19:40:01
or 5040

momoshi 2010-09-22 19:40:01
7! or 5040 ways

2012 2010-09-22 19:40:01
The answer is 5040

number.sense 2010-09-22 19:40:04
5040=7!

rrusczyk 2010-09-22 19:40:13
Indeed, multiplying out 7!, we get 5040.

rrusczyk 2010-09-22 19:40:20
That problem was pretty simple. Let's put a wrinkle in it. Suppose we must have a girl in the first chair and a girl in the last chair. Then how many seatings are there?

rrusczyk 2010-09-22 19:40:28
What's wrong with this answer:

rrusczyk 2010-09-22 19:40:34
There are 4 ways to choose the girl for the first chair. After that, we have 6 students left for the next chair, then 5 for the next, and so on, giving us a total of:

rrusczyk 2010-09-22 19:40:38
4 x 6 x 5 x 4 x 3 x 2 x 1 seatings.

rrusczyk 2010-09-22 19:40:42
What's wrong with that?

catlover114 2010-09-22 19:41:08
girl in last chair

Orange-2728 2010-09-22 19:41:08
there has to be a girl at the end

ksun48 2010-09-22 19:41:08
the last chair might be a boy

Qazmaz 2010-09-22 19:41:08
there is a limtied amount of girls

professordad 2010-09-22 19:41:08
the last person could be a boy or girl by that method

rrusczyk 2010-09-22 19:41:13
The problem here is the last chair - we must have a girl in that last chair, but our approach above definitely does not guarantee this. We might end up with a boy left at the end, which would violate the problem.

rrusczyk 2010-09-22 19:41:18
What do we have to do to deal with this?

iwinforthewin 2010-09-22 19:41:51
so do first and last chairs first, then deal with middle ones

$LaTeX$ 2010-09-22 19:41:51
select the girl that sits at the end first

catlover114 2010-09-22 19:41:51
deal with 1st and last chairs first, then the rest

theorist2 2010-09-22 19:41:59
assign the end chairs first

rrusczyk 2010-09-22 19:42:02
We can think to ourselves 'How would we seat the kids according to these restrictions if we had to make up a seating ourselves?' Our answer is: we'd seat the girls at the ends first, so we make sure we satisfy that restriction. What do we find?

rrusczyk 2010-09-22 19:42:53
What do we get for the number of seatings?

joyofpi 2010-09-22 19:43:29
We have 4 ways for the first girl, 3 for the last girl and then 5! for the middle ones so we multiply them to get 1440

professordad 2010-09-22 19:43:29
4*5*4*3*2*1*3

$LaTeX$ 2010-09-22 19:43:29
4*3*5!=12*120=1440

number.sense 2010-09-22 19:43:29
4*5*4*3*2*1#=1440 ways

Qazmaz 2010-09-22 19:43:29
is it 4x3x5!

mackamom 2010-09-22 19:43:29
4*5*4*3*2*3

anumoluha 2010-09-22 19:43:35
4 x 3 x 5 x 4 x 3 x 2 x 1

theorist2 2010-09-22 19:43:37
4*3*5*4*3*2

rrusczyk 2010-09-22 19:43:42
As before, there are 4 ways to seat a girl in the first seat. Next we seat a second girl in the last seat - there are 3 girls left, so there are 3 choices. Now we have our restriction taken care of. We can then seat the rest of the students as before. There are 5 students left to choose one for the second chair, then 4 students for the third chair, and so on.

rrusczyk 2010-09-22 19:43:52
Thus, we have 4 x 3 ways to seat girls at each end, and for each of these seatings we have 5 x 4 x 3 x 2 x 1 ways to seat the rest of the students, for a total of:

rrusczyk 2010-09-22 19:43:56
4 x 3 x 5 x 4 x 3 x 2 x 1 = 1440

rrusczyk 2010-09-22 19:44:03
ways to seat the students such that there is a girl on either end.

rrusczyk 2010-09-22 19:44:16
This example brings up two important counting concepts.

rrusczyk 2010-09-22 19:44:22
First, when dealing with a counting problem that has restrictions, it often pays to think about how you would create one possible arrangement yourself. Here, we realize that if we seated the students ourselves, we'd start with the girls on the ends. This brings us to our second important counting concept:

rrusczyk 2010-09-22 19:44:31
When dealing with restrictions, it usually helps to deal with the restrictions first. Here, we took care of the girls on the ends first since that was our restriction.

rrusczyk 2010-09-22 19:44:42
However, there are other clever ways for dealing with restrictions. Let's check a couple others out:

rrusczyk 2010-09-22 19:44:46
We still have 7 students to seat in a row, but two of them, Ali and Brianna, refuse to sit next to each other. In how many ways can we seat the students now?

rrusczyk 2010-09-22 19:44:53
What's wrong with this solution:

rrusczyk 2010-09-22 19:44:59
There are 7 ways to seat Ali. We deal with the restriction first and realize that we can't seat Brianna in either of the seats next to Ali. Hence, Brianna has 4 choices. Then the next student has 5 choices, the one after that has 4 choices, and so on.

rrusczyk 2010-09-22 19:45:03
What's wrong?

$LaTeX$ 2010-09-22 19:45:48
what if Ali sits at the end?

Tigris 2010-09-22 19:45:48
Ali may sit at the end chair

ln25e6 2010-09-22 19:45:48
Ali can sit on the end.

anumoluha 2010-09-22 19:45:48
if ali is seated on either end, brianna has 5 choices, not 4

theorist2 2010-09-22 19:45:56
Ali could be at an end, giving B 5 choices

nwalton125 2010-09-22 19:46:00
if Ali sits on an end, Brianna has 5 choices

rrusczyk 2010-09-22 19:46:01
The problem here is that there are not always 2 seats next to Ali - sometimes he may be put at the end. Hence, sometimes Brianna will have 5 choices for her seat.

rrusczyk 2010-09-22 19:46:08
We could deal with this by using casework (and we'll discuss very important casework strategies in the course - these tricky casework problems are often the difference in proceeding to the next level in MATHCOUNTS/AMC), but there is a slicker approach. What else could we do?

2012 2010-09-22 19:46:45
WE can count all the cases

rrusczyk 2010-09-22 19:46:48
Then what?

catlover114 2010-09-22 19:47:28
subtract where they are next to each other from the total

$LaTeX$ 2010-09-22 19:47:28
count the number of ways that they can't sit and then subtract from the total

$LaTeX$ 2010-09-22 19:47:28
subtract the number of ways that ali and brianna are next to each other

danny96221 2010-09-22 19:47:28
subtract the unnecessary

ln25e6 2010-09-22 19:47:28
count the wrong answers and subtract.

rrusczyk 2010-09-22 19:47:32
What makes this problem hard is the restriction that Ali and Brianna are not adjacent. We know there are 7! ways to seat the students without any restrictions.

rrusczyk 2010-09-22 19:47:39
Instead of counting our desired seatings directly, we count what we don't want and subtract.

rrusczyk 2010-09-22 19:47:52
We know there are 7! ways without restrictions, so we will try to count those that violate our restriction that Ali and Brianna are separate. We'll then subtract these violators from our total.

rrusczyk 2010-09-22 19:47:59
In how many ways can we seat Ali and Brianna if they are together?

catlover114 2010-09-22 19:49:04
12

nwalton125 2010-09-22 19:49:04
oops, 12

rrusczyk 2010-09-22 19:49:07
Why?

$LaTeX$ 2010-09-22 19:49:37
since 6 places to put them next to each other

$LaTeX$ 2010-09-22 19:49:37
and then 2 to arrange them when they're next to each other

catlover114 2010-09-22 19:49:39
6 ways to choose which 2 seats, out of those 2 2 ways to arrange.

number.sense 2010-09-22 19:49:39
there are 6 ways to seat them together, but you can change order of a and b

Caphi100 2010-09-22 19:49:44
they can be seated 6 ways, and they can switch seats

rrusczyk 2010-09-22 19:49:50
There are 6 pairs of consecutive seats.

yangboda 2010-09-22 19:50:07
Because, 6 ways to chose 2 seats, out of the other ways to organize

Qazmaz 2010-09-22 19:50:07
6 ways 2 different ways to sit and switch

rrusczyk 2010-09-22 19:50:13
Once we choose their seats, there are 2 ways to put them in the chairs we choose.

rrusczyk 2010-09-22 19:50:31
So, are there a total of 6*2 = 12 seatings with Ali and Brianna together?

catlover114 2010-09-22 19:51:07
no,the other people still have choices.

Tigris 2010-09-22 19:51:07
no. other kids may sit at other sits

$LaTeX$ 2010-09-22 19:51:07
u have to arrange the other 5 people

danny96221 2010-09-22 19:51:16
no because other people are arrnaged

rrusczyk 2010-09-22 19:51:18
Oh yeah, we can't forget the others!

rrusczyk 2010-09-22 19:51:24
How can we account for them?

nwalton125 2010-09-22 19:52:11
12*5!, because you have to account for the others

$LaTeX$ 2010-09-22 19:52:11
so 12 * 5! = 1440

catlover114 2010-09-22 19:52:11
give the others 5! ways to arrange themselves

ln25e6 2010-09-22 19:52:11
multiply by 5!

rrusczyk 2010-09-22 19:52:16
We must seat the other 5 people. There are 5! ways to seat these people in the remaining chairs for each of the 12 ways Ali and Brianna can sit, so there are 12*5! seatings with Ali and Brianna together.

rrusczyk 2010-09-22 19:52:24
Here's another way to think about it:

theorist2 2010-09-22 19:52:26
Treat A-B as one person (aliBaba?), this gives 6! ways to seath the now 6 people. But considering that Ali and Briana can sit on either side of each other, multiply by two. This yields 6! * 2e

rrusczyk 2010-09-22 19:52:35
Now, we have to answer the original question.

rrusczyk 2010-09-22 19:52:55
We want to know the number of ways to seat them so that Ali and Brianna are SEPARATED, not together.

number.sense 2010-09-22 19:53:40
3600 ways

danny96221 2010-09-22 19:53:40
subract 1440 from 7!=5040 getting 3600 :D

$LaTeX$ 2010-09-22 19:53:40
its 7!-12*5!=5040-1440=3600

Orange-2728 2010-09-22 19:53:40
3600

catlover114 2010-09-22 19:53:40
subtract from 7!

$LaTeX$ 2010-09-22 19:53:40
subtract 1440 from 5040 (7!)

rrusczyk 2010-09-22 19:53:43
There are 7! ways without restrictions, and 12 x 5! ways for them to be together. This leaves 7! - 12 x 5! ways for them to be apart. Computing this, we get 3600 seatings.

rrusczyk 2010-09-22 19:53:54
This example brings up a couple more important tactics.

rrusczyk 2010-09-22 19:54:00
First, when it looks hard to count something directly, try counting the opposite of what you're asked for. We call this approach complementary counting, since 'complement' in dealing with groups of objects in mathematics roughly means 'opposite'. I also call this 'counting what you don't want'.

rrusczyk 2010-09-22 19:54:33
Second, when your restriction is that some of your items must remain together when putting them in a row, a useful tactic is to consider the items all together as a single item, as theorist2 did aliBaba above. Then you separately consider how many ways you can order the items within the group.

rrusczyk 2010-09-22 19:54:43
These three basic examples show why it is pointless to memorize your way through counting - I can ask zillions of variations of the above questions. Instead of memorizing your way through each variation, you should learn when to add, when to subtract, when to multiply, and when to divide. Since you already know how to perform these operations, once you know when to do them, you know how to count!

rrusczyk 2010-09-22 19:54:54
The first of these three problems was considerably easier than most of the problems we will do in the Introduction to Counting & Probability course. The second and third are a little closer to the middle in difficulty, though they are still a good bit easier than the average problem.

rrusczyk 2010-09-22 19:55:03
In general in the course we will go through the ideas more gradually than we did here - each idea will be explored with gradually more difficult examples. Thus, the pace at which new ideas are introduced is a little slower than we did here (in which we introduced 4 general tactics in two problems!)

yangboda 2010-09-22 19:55:06
what other ways can you use complementary counting

rrusczyk 2010-09-22 19:56:05
You'll see tons of examples in the Intro to Counting & Probability course. Any time you have problems counting something directly, you can consider trying complementary counting. This is especially true when the "no restrictions" is easy to count, like the "all seatings" here.

rrusczyk 2010-09-22 19:56:10
Now, let's take a look at a couple counting problems with a number theory taste.

rrusczyk 2010-09-22 19:56:18
COUNTING DIVISORS

rrusczyk 2010-09-22 19:56:22
Once we know how to find the prime factorization of numbers, we can begin to use this tool to solve other problems.

rrusczyk 2010-09-22 19:56:28
One such problem is answering the question, 'How many positive divisors does a particular integer have?' This kind of counting problem is common in number theory.

rrusczyk 2010-09-22 19:56:33

rrusczyk 2010-09-22 19:56:50
How can we describe any divisor of 200?

Qazmaz 2010-09-22 19:57:20
divisible by 2 and 5

joyofpi 2010-09-22 19:57:20
its divisible by 2 or 5

anumoluha 2010-09-22 19:57:20
a multiple of 2 or 5

momoshi 2010-09-22 19:57:20
it is a multile of 2 and/or 5

rrusczyk 2010-09-22 19:57:39
Indeed it must be a multiple of 2 and/or 5. Is that a strong enough condition?

$LaTeX$ 2010-09-22 19:58:07
no

iwinforthewin 2010-09-22 19:58:07
no

catlover114 2010-09-22 19:58:07
no, can't have > 3 2's or >2 5's.

rrusczyk 2010-09-22 19:58:11
That's not quite strong enough! 30 is a multiple of 2 and of 5, but it is not a divisor of 200.

momoshi 2010-09-22 19:58:20
yes

danny96221 2010-09-22 19:58:20
it must be in a form 2^a1 x 5^a2 such that a1 < 3 and a2 < 5

iwinforthewin 2010-09-22 19:58:31
1000 is a multiple of 2 and 5, but it is not a factor

rrusczyk 2010-09-22 19:58:52
Good point. It's not enough just to say "it only has 2 and 5 in its prime factorization".

rrusczyk 2010-09-22 19:59:51
It is true that:

rrusczyk 2010-09-22 19:59:53

rrusczyk 2010-09-22 20:00:09

$LaTeX$ 2010-09-22 20:00:51
where a<=3 and b<=2, and both are non-negative

2012 2010-09-22 20:00:51
a<=3, b<=2

2012 2010-09-22 20:00:51
a<=3,b<=2, including a=0, b=0

rrusczyk 2010-09-22 20:01:08

rrusczyk 2010-09-22 20:01:14
Now that you know what the possible values for a and b are, how can you use this to count the total number of divisors of 200?

$LaTeX$ 2010-09-22 20:02:49
you have 4 choices for the power of 2 and 3 choices for the power of 5, so there are 3*4 = 12 divisors of 200

catlover114 2010-09-22 20:02:49
4 different ways for 2's, 3 different ways for 5's, so 4*3=12

professordad 2010-09-22 20:02:49

bryanxqchen 2010-09-22 20:02:49
4*3

princesssnigdha 2010-09-22 20:02:56
12

rrusczyk 2010-09-22 20:02:58
Consider this tree diagram:

rrusczyk 2010-09-22 20:03:03

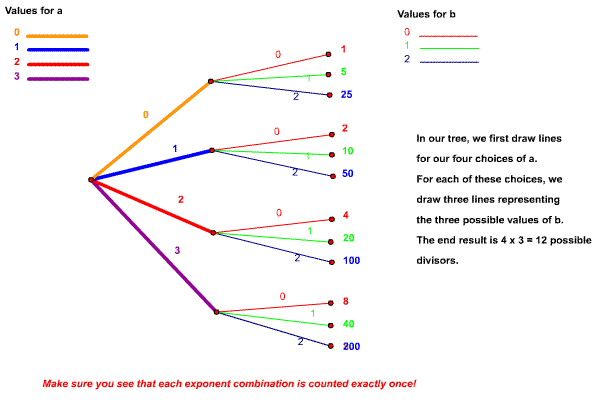
rrusczyk 2010-09-22 20:03:20

rrusczyk 2010-09-22 20:03:34
Indeed we can see that this is true by listing the divisors:
1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, and 200 are all the positive divisors of 200.

rrusczyk 2010-09-22 20:03:41
So, why is it that we multiply the number of possible values for the exponent of each prime together?

iwinforthewin 2010-09-22 20:04:26
you are counting the number of combinations, so you multiply]

professordad 2010-09-22 20:04:26
because we can have any combination of those numbers.

momoshi 2010-09-22 20:04:26
is it like one of those clothing combination problems

Orange-2728 2010-09-22 20:04:32
because those are all the possible combinations

catlover114 2010-09-22 20:04:32
they're independent but related: they don't affect each other but they're both included in the result

rrusczyk 2010-09-22 20:04:58
I like the "clothing combination" comparison: we are dressing the 2 with an exponent, and dressing the 5 with an exponent...

myth17 2010-09-22 20:05:00
you know the number of choices possible for each factor. by multiplying the amount of possibilities for each factor you find the amount of divisors

rrusczyk 2010-09-22 20:05:03
The reason we simply multiply the numbers of values for the exponents together is because we can select the values for each exponent independently from the values of the other exponent(s).

rrusczyk 2010-09-22 20:05:09

rrusczyk 2010-09-22 20:05:13

rrusczyk 2010-09-22 20:05:18
So, in general, how do we find the total number of divisors of an integer n?

$LaTeX$ 2010-09-22 20:06:26
you add one to all the powers, then multiply

number.sense 2010-09-22 20:06:26
add 1 to each of powers in p.f. and multiply

professordad 2010-09-22 20:06:26
add 1 to all the exponents and multiply all the new numbers

catlover114 2010-09-22 20:06:26
n = p^a * p^b*...

catlover114 2010-09-22 20:06:26
then (a+1)(b+1)...

rrusczyk 2010-09-22 20:06:31

rrusczyk 2010-09-22 20:06:39

rrusczyk 2010-09-22 20:06:57
We do this for each prime factor in the original number, and then we multiply all the results (for the reason we saw in the tree, or in the table). That gives us the total number of divisors.

rrusczyk 2010-09-22 20:07:03
To make this method more clear, we will now work through a couple exercises.

rrusczyk 2010-09-22 20:07:11
How many positive divisors does 60 have?

rrusczyk 2010-09-22 20:07:16
Where do we start?

Caphi100 2010-09-22 20:07:36
find the prime factors

bryanxqchen 2010-09-22 20:07:36
prime factorize it

2012 2010-09-22 20:07:36
Prime Factorize 60

princesssnigdha 2010-09-22 20:07:36
prime factorization

anumoluha 2010-09-22 20:07:36
the p.f. of 60

Curtis 2010-09-22 20:07:38
primefactorization

rrusczyk 2010-09-22 20:07:46
And what is that prime factorization?

myth17 2010-09-22 20:08:11
p.f. of 60 is 2*2*3*5

number.sense 2010-09-22 20:08:11
2^2*5*3

$LaTeX$ 2010-09-22 20:08:11

catlover114 2010-09-22 20:08:11
2*2*3*5

iwinforthewin 2010-09-22 20:08:11
2^2x3x5

Orange-2728 2010-09-22 20:08:11
2^2*3*5

myth17 2010-09-22 20:08:11
2^2 *3*5

ln25e6 2010-09-22 20:08:11
2^2*3*5

anumoluha 2010-09-22 20:08:11
3 x 5 x 2^2

rrusczyk 2010-09-22 20:08:16

amazazing 2010-09-22 20:08:17
2^2*3*5

rrusczyk 2010-09-22 20:08:33
So, how many divisors are there?

number.sense 2010-09-22 20:09:03
12

ahaanomegas 2010-09-22 20:09:03

catlover114 2010-09-22 20:09:03
3*2*2=12

iwinforthewin 2010-09-22 20:09:03
(2)(3)(2) = 12

$LaTeX$ 2010-09-22 20:09:03

myth17 2010-09-22 20:09:03
so (2+1) (1+1) (1+1)=12

cathy_fong 2010-09-22 20:09:03
there are 12

momoshi 2010-09-22 20:09:03
12 divisors

amazazing 2010-09-22 20:09:07
3*2*2=12

$LaTeX$ 2010-09-22 20:09:08

rrusczyk 2010-09-22 20:09:11

rrusczyk 2010-09-22 20:09:16

rrusczyk 2010-09-22 20:09:21

rrusczyk 2010-09-22 20:09:32
One last problem coming up!

rrusczyk 2010-09-22 20:09:38
Find the number of positive divisors of 792 that are even.

rrusczyk 2010-09-22 20:09:58
We'll get started on this by solving an easier problem (that's the way I do a lot of hard problems).

rrusczyk 2010-09-22 20:10:00
First, how many positive divisors does 792 have?

ahaanomegas 2010-09-22 20:10:08
Start with the Prime Factorization again

rrusczyk 2010-09-22 20:10:12
OK, what is it?

bryanxqchen 2010-09-22 20:10:39

myth17 2010-09-22 20:10:39
the p.f. of 792 is 2^3 *3^2 *11

$LaTeX$ 2010-09-22 20:10:39

catlover114 2010-09-22 20:10:39
2*2*2*3*3*11

ahaanomegas 2010-09-22 20:10:39

iwinforthewin 2010-09-22 20:10:39
792 = 2^3*11*3^2

amazazing 2010-09-22 20:10:39
2^3*3^2*11

rrusczyk 2010-09-22 20:10:43

rrusczyk 2010-09-22 20:10:49
How many divisors total are there?

$LaTeX$ 2010-09-22 20:11:06

Qazmaz 2010-09-22 20:11:06
24

iwinforthewin 2010-09-22 20:11:06
that gives you 4x3x2 factors total

number.sense 2010-09-22 20:11:06
24

YasserR 2010-09-22 20:11:06
24

Curtis 2010-09-22 20:11:06
24

theorist2 2010-09-22 20:11:06
4*3*2

ahaanomegas 2010-09-22 20:11:06
24

catlover114 2010-09-22 20:11:06
24

rrusczyk 2010-09-22 20:11:10

myth17 2010-09-22 20:11:40
you must have a positive integer for the exponent of 2, so 3*3*2

bryanxqchen 2010-09-22 20:11:40

theorist2 2010-09-22 20:11:40
3*3*2 = 18

ahaanomegas 2010-09-22 20:11:40

catlover114 2010-09-22 20:11:40
even must have a 2 in it, so 18

ln25e6 2010-09-22 20:11:40
18

rrusczyk 2010-09-22 20:11:51

rrusczyk 2010-09-22 20:11:59

rrusczyk 2010-09-22 20:12:05

iwinforthewin 2010-09-22 20:12:07
couldn't you just divide 792 by 2 and get 396, and find its factors

rrusczyk 2010-09-22 20:12:16
Will that work?

catlover114 2010-09-22 20:13:08
hmmm... works in this scenario...

rrusczyk 2010-09-22 20:13:16
Indeed, but will it always work?

rrusczyk 2010-09-22 20:13:30
I see some of you saying not always.

rrusczyk 2010-09-22 20:13:36
And others saying yes.

rrusczyk 2010-09-22 20:13:46
But I don't see a convincing explanation yet!

rrusczyk 2010-09-22 20:14:32
(To be clear: iwinforthewin is not saying that the divisors of 396 are the even divisors of 792. iwinforthewin is saying that there are exactly as many divisors of 396 as there are even divisors of 792.)

$LaTeX$ 2010-09-22 20:15:01
you divided out the 2, so the divisors of 396 multiplied by 2, must be an even divisor of 792

NYCDL 2010-09-22 20:15:02
Yes, it will. After finding all the factors of 396, they will multiply back with 2. This will yield all even factors.

number.sense 2010-09-22 20:15:02
yes because dividing by 2 just takes out the extra 2^0 term

iwinforthewin 2010-09-22 20:15:02
it should work because you took one less power of two from 792, and by dividing by 2, you get the same number if you * it out.

aamontree 2010-09-22 20:15:12
actually that might work...

rrusczyk 2010-09-22 20:15:15
Yep!

rrusczyk 2010-09-22 20:15:33
To make an even divisor of 792, we can take a divisor of 396 (half of 792) and multiply it by 2.

rrusczyk 2010-09-22 20:15:54
Going the other direction, if we halve any even divisor of 792, we get a divisor of 396.

rrusczyk 2010-09-22 20:16:13
We call this a 1-to-1 correspondence, which we study much more in the Intermediate Counting & Probability class.

cathy_fong 2010-09-22 20:16:23
ohh so it does work

rrusczyk 2010-09-22 20:16:26
Exactly.

rrusczyk 2010-09-22 20:16:36
While the discussion tonight was similar to that in our classes, there are a few BIG differences between tonight and the typical class.

rrusczyk 2010-09-22 20:16:42
There is a much wider range of students here tonight than in our typical classes. So, some of you will find tonight's material very, very easy, and others will find it very, very hard. Also, because there's such a wide spread of students, we typically end up going a bit faster in the Math Jam than we do in class.

rrusczyk 2010-09-22 20:16:52
Furthermore, there are many more students here tonight than in a typical class. In our classes, we get to all the student questions, and everyone who is participating gets lots of "air time" in the classroom. We also often have an extra assistant in our usual classes.

rrusczyk 2010-09-22 20:17:09
If you have any math questions about the problems we did tonight, ask them now, and Ariana will help you.

rrusczyk 2010-09-22 20:17:14
That's it for the math tonight. We will now discuss the courses.

rrusczyk 2010-09-22 20:17:38
All of our courses offer full transcripts for each class, so if you're going to miss some classes, you'll still have access to everything that happened in class. Moreover, you'll be able to use the course message board to ask any questions you have outside of class time.

rrusczyk 2010-09-22 20:17:43
We have two new courses this fall. We are launching our computer science curriculum with an Introduction to Programming course, and we are offering an exploration of powerful higher mathematics in a Group Theory course.

rrusczyk 2010-09-22 20:17:53
[u]Introductory level: Grades 6-10[/u]
Algebra 1: Tues, Sept 14 - Jan 11, 1 PM - 2:30 PM ET (10 AM - 11:30 AM PT)
Algebra 1: Mon, Oct 4 - Jan 31
Introduction to Counting & Probability: Wed, Oct 13 - Jan 19
Introduction to Number Theory: Fri, Oct 8 - Jan 14
Algebra 2: Tues, Sept 28 - Jan 25
Introduction to Geometry: Thurs, Sept 30 - Mar 31
MATHCOUNTS/AMC 8 Basics: Thurs, Oct 7 - Jan 13
Advanced MATHCOUNTS/AMC 8: Tues, Oct 5 - Jan 11
Advanced MATHCOUNTS/AMC 8: Wed, Dec 1 - Mar 2

rrusczyk 2010-09-22 20:18:00
Unless otherwise noted, classes for each course are once a week, 7:30 PM - 9 PM ET (4:30 PM - 6 PM PT).

rrusczyk 2010-09-22 20:18:09
[u]Intermediate level: Grades 8-12[/u]
Algebra 3: Mon, Oct 4 - Apr 4
Intermediate Number Theory: Fri, Oct 1 - Nov 19
Precalculus: Wed, Oct 6 - Feb 23
AMC 10 Problem Series: Mon, Oct 18 - Jan 24 (9-10:30 PM ET/6-7:30 PM PT)
AMC 12 Problem Series: Mon, Sept 13 - Dec 6
AMC 12 Problem Series: Wed, Oct 20 - Jan 26 (9-10:30 PM ET/6-7:30 PM PT)
AIME Problem Series A: Tues, Aug 31 - Nov 16 (9-10:30 PM ET/6-7:30 PM PT)
AIME Problem Series A: Fri, Dec 3 - Mar 4
AIME Problem Series B: Thurs, Dec 2 - Mar 3

rrusczyk 2010-09-22 20:18:15
[u]Advanced[/u]
Calculus: Tues, Sept 28 - Apr 5 (7:30 - 9:30 PM ET/4:30 - 6:30 PT)
Group Theory: Wed, Oct 6 - Jan 26 (7:30 - 9:30 PM ET/4:30 - 6:30 PT)
WOOT!: Sept - April

rrusczyk 2010-09-22 20:18:23
[u]Computer Science/Programming[/u]
Introduction to Programming: Thurs, Sept 16 - Dec 9
Introduction to Programming: Wed, Sept 22 - Dec 15

rrusczyk 2010-09-22 20:18:29
More details about each course can be found by clicking the appropriate course name here:

rrusczyk 2010-09-22 20:18:36
http://www.artofproblemsolving.com/School/classlist.php

rrusczyk 2010-09-22 20:19:06
We offer two types of classes: subject classes and contest prep "problem series" courses. Each course has its own course homepage for enrolled students. On the course homepage, there is a variety of information about the course. Each course also has its own message board on which students can ask questions outside class time. Students even have the ability to ask questions anonymously by using an "Ask a Question" feature on the course homepage.

rrusczyk 2010-09-22 20:19:25
After class each week, we make a class transcript available on the course homepage. So, if you miss a class, you still have access to everything that happened in class. The class transcript also frees you from having to take notes during class. Instead of copying everything down during class, you can focus on the math and think about the problems. The transcript will be there later when you want to review.

rrusczyk 2010-09-22 20:19:36
We also place problems on the course message board for the students to discuss. The following week, we post solutions to the problems.

rrusczyk 2010-09-22 20:19:51
There is an accompanying textbook for most of the subject classes (not the contest prep problem series courses, nor for Intermediate Number Theory or Group Theory). For each of these courses, there are corresponding readings in the textbook each week. As you might expect, students who work with the textbook in addition to attending class get a lot more out of the courses! The appropriate chapters for each week are listed in the Course Information document that students can access on the course homepage upon enrolling.

rrusczyk 2010-09-22 20:20:12
The other main difference between the subject classes and the problem series courses is that each subject course (besides Intermediate Number Theory) has longer problem sets called Challenge Sets roughly every three weeks. These are the primary homework assignments for the subject classes. Students should write up full solutions and submit them to us for evaluation (there are thorough instructions for how to do so on each Challenge Set). These solutions will be evaluated by AoPS graders, and you will receive detailed feedback.

rrusczyk 2010-09-22 20:20:31
There are diagnostic tests available for each of the subject classes. You can find these on the Class Schedule page here: http://www.artofproblemsolving.com/School/classlist.php

rrusczyk 2010-09-22 20:20:45
To get the most out of the courses, students should spend 5-7 hours/week on the subject courses and 3-4 hours/week on the problem series courses (including class time).

rrusczyk 2010-09-22 20:20:52
I'll take questions about the courses now. Here's the schedule again:

rrusczyk 2010-09-22 20:20:56
http://www.artofproblemsolving.com/School/classlist.php

rrusczyk 2010-09-22 20:21:02
Please note that I'll probably have a *lot* of questions tonight, so it might take me a little while to get to yours. But I will try to get to all of them!

rrusczyk 2010-09-22 20:21:15
Please only ask your question once unless I haven't answered it for 10 minutes or so.

rrusczyk 2010-09-22 20:21:22
I will have a queue of questions, and will get to them all.

Birbal 2010-09-22 20:21:33
I have a question. I've just been put into an accelerated math class at my school. In it, we cover alegbra 2 and precalculus. I have some catching up to do in algebra but dont want to fall behind in precalculus. I was wondering if I should take precalculus and algebra 2 at the same time or algebra first and precalculus second.

rrusczyk 2010-09-22 20:22:15
Our Algebra 2 and Precalculus course are far apart in difficulty. If you are concerned about your algebra background, go for the Algebra 2 class. Also, much of our Precalculus course is way beyond what you'll see in your school.

koek67 2010-09-22 20:22:17
does the 5-7 hours include the class time

rrusczyk 2010-09-22 20:22:20
Yes

Qazmaz 2010-09-22 20:22:33
do we have to already know number theory or probability

rrusczyk 2010-09-22 20:22:34
Not if you are enrolling in the Intro courses.

rober5x7 2010-09-22 20:22:43
is advanced mathcounts hard nats?

rrusczyk 2010-09-22 20:22:57
Yes, that course is aimed at students preparing for Nationals (or for State competitions)

LotharCollatz 2010-09-22 20:23:03
How do the intermidate level courses compare in dificulty to the AIME prep courses and WOOT?

rrusczyk 2010-09-22 20:23:29
Wider range of difficulty than AIME (more easy stuff, and more hard stuff). Not as hard as WOOT.

Orange-2728 2010-09-22 20:23:33
WOOT??

rrusczyk 2010-09-22 20:23:56
Our high school olympiad training program:

rrusczyk 2010-09-22 20:23:57
http://www.artofproblemsolving.com/School/woot.php

momoshi 2010-09-22 20:24:02
are all of these classes free?

rrusczyk 2010-09-22 20:24:17
No; the fees are on the class list page linked at the top of this page.

Orange-2728 2010-09-22 20:24:22
what is the difference between Number THeory and Counting and Probability

rrusczyk 2010-09-22 20:24:36
You can look at the class descriptions by clicking the appropriate classes here:

rrusczyk 2010-09-22 20:24:41
http://www.artofproblemsolving.com/School/classlist.php

rrusczyk 2010-09-22 20:24:46
They are different areas of math.

harukikara 2010-09-22 20:24:51
would we learn probability in either of the number theory classes or is it only in the counting and probability class?

rrusczyk 2010-09-22 20:24:58
Just the counting & probability class.

aamontree 2010-09-22 20:25:31
Can you take both classes?

rrusczyk 2010-09-22 20:25:33
Yes

theorist2 2010-09-22 20:25:35
How do the help and resources outside of the online classroom differ between the subject courses and the problem series? notes, problem sets, graded solutions ... ?

rrusczyk 2010-09-22 20:25:36
There are no graded Challenge Sets in the problem series, and there is no textbook. There are no course notes in the problem series either.

aamontree 2010-09-22 20:26:05
If we are lets say scoring a 80-90 on the AMC 10. Do you recomend taking the AMC PRoblem Series Class? Or will that be much too difficult?

rrusczyk 2010-09-22 20:26:07
The AMC 10 class could be a fine fit for you, as would the various Introduction level courses.

catlover114 2010-09-22 20:26:33
are there specific contest score cutoffs for the Advanced Contest class?

rrusczyk 2010-09-22 20:26:35
No; it's mainly students preparing for State or Nationals in MATHCOUNTS.

yangboda 2010-09-22 20:27:00
Right now, my school is studying algebra 1, yet I want to get ahead and start doing some more exercises ahead of time. What do you suggest?

rrusczyk 2010-09-22 20:27:02
Get our Introduction to Algebra book and/or enroll in the Algebra 1 course. We'll be way ahead of your school in no time.

LotharCollatz 2010-09-22 20:27:15
what is covered in the precalculus course?

rrusczyk 2010-09-22 20:27:24
Trig, complex numbers, and beginning linear algebra.

rrusczyk 2010-09-22 20:27:30
Here's a more detailed list:

rrusczyk 2010-09-22 20:27:30
http://www.artofproblemsolving.com/School/courseinfo.php?course_id=precalc

yangboda 2010-09-22 20:27:43
what do you suggest for a middle school student

rrusczyk 2010-09-22 20:28:03
Usually, middle school students take our Intro level subject courses and/or the MATHCOUNTS/AMC 8 problem series course.

anumoluha 2010-09-22 20:28:05
Do you have a list of schools that accept credits from your AoPS courses?

rrusczyk 2010-09-22 20:28:20
No; students sort that out with their own schools on a case-by-case basis.

Birbal 2010-09-22 20:28:22
are we going to get a transcript of this "class"

rrusczyk 2010-09-22 20:28:32
It will be here:

rrusczyk 2010-09-22 20:28:33
http://www.artofproblemsolving.com/School/mathjams.php?past=1

rrusczyk 2010-09-22 20:28:40
Probably a half hour after we finish.

koek67 2010-09-22 20:28:44
do you have any courses in summer

rrusczyk 2010-09-22 20:28:52
Many. We'll have the schedule up around year-end.

momoshi 2010-09-22 20:28:57
What would you reccomend for me I have been to the chapter twice in mathcounts. I have also, finished algebra 1 and am taking geometry this year.

rrusczyk 2010-09-22 20:29:22
Intro Counting & Probability or Intro Number Theory. You'll see a lot of good stuff that you won't see in school, but will see in MATHCOUNTS (or other areas of study).

poingu 2010-09-22 20:30:07
My son is in Algebra 1 now and loves it but I'm worried he'll get discouraged at the pace. He's 10 so there is plenty of time...but if we decide it's too hard, would you recommend one of the problem solving courses as a good way to ready himself? Or to take Algebra 1 twice? He -is- enjoying it but I could see it getting harder this week...

rrusczyk 2010-09-22 20:30:10
10 is young, indeed. The MATHCOUNTS/AMC 8 Basics is a good bit lighter in the workload and intensity.

Curtis 2010-09-22 20:30:51
how hard is intermediate number theory compare to intro to number theroy, what age should you be?

rrusczyk 2010-09-22 20:30:53
It's not so much age as math experience. You should know modular arithmetic, and have a good handle on algebra up through Algebra 2.

LotharCollatz 2010-09-22 20:31:05
How much easeir is the AMC12 class compared to AIME A

rrusczyk 2010-09-22 20:31:07
About as much easier as the AMC 12 is than the AIME.

Curtis 2010-09-22 20:31:12
do we take amc8 in 8th grade?

rrusczyk 2010-09-22 20:31:18
In or before the 8th grade.

koek67 2010-09-22 20:31:21
I am enrolled to do introduction to Geometry. If I have a question in the middle of the week, can I still post the question and get an answer

rrusczyk 2010-09-22 20:32:00
Absolutely! You can post it on the course message board, or you can use the Ask a Question feature on the course homepage, which will post the question on the message board for you (and email the instructor that a question is there).

number.sense 2010-09-22 20:32:34
is there any possibility of an AOPS linear algebra course in the future?

rrusczyk 2010-09-22 20:32:36
Some possibility. There's a lot of linear algebra in the Precalc class (enough to get you through a collegiate physics or multivariable calc course, for example)

Qazmaz 2010-09-22 20:32:53
does this class count for credits like in high school or something?

rrusczyk 2010-09-22 20:32:54
It can in some schools, but you have to get your school to agree to it.

LotharCollatz 2010-09-22 20:32:59
Is there a continuation of WOOT/ something similar offered during the summer?

rrusczyk 2010-09-22 20:33:13
Not something like WOOT, but there will be some Intermediate courses.

theorist2 2010-09-22 20:33:16
I understand that if I acccidentally register for a class that torns out to be a poor fit I can request a refund before the 3rd class. Does this apply if I'm using a gift certificate to partially pay for the course? If I drop the course after one or two classes, could I still use the gift certificate on another course of books?

rrusczyk 2010-09-22 20:33:19
Yes and yes

danny96221 2010-09-22 20:33:24
i am confident in the amcs, scoring 120 +, but i feel i have a weak basis, which causes problems in aime level problems.what would you recommend?

rrusczyk 2010-09-22 20:33:46
Work through AoPS Volume 1. And if there's a particular subject that gives you problems, use the corresponding Intro book.

Saraswati Devi 2010-09-22 20:34:01
What topics show up the most in MATHCOUNTS?

rrusczyk 2010-09-22 20:34:03
Hard to answer. It's usually a good mix!

princesssnigdha 2010-09-22 20:34:19
I am studying Algebra I in my school and has been working on your algebra book. What class would you suggest for me? I want to prepare for Mathcounts and have no exposure to probability and geometry sections.

rrusczyk 2010-09-22 20:34:20
Intro Counting & Probability would be a good course for you.

load 2010-09-22 20:34:23
Is Intermediate Number Theory good for AMC12 more, or the AIME?

rrusczyk 2010-09-22 20:34:35
Both, with a bit of a bias towards the AIME

Dsquared 2010-09-22 20:34:38
So you can take amc8 in 7th grade?

rrusczyk 2010-09-22 20:34:40
Yes

bulutcocuk 2010-09-22 20:34:42
will the intermediate c/p help with high level AIME? (problems 8-15)

rrusczyk 2010-09-22 20:34:53
Definitely; we have many problems of that difficulty in the course and book.

momoshi 2010-09-22 20:34:55
i am EXTREMELY busy on weekdays. can you please create some introductory weekend classes

rrusczyk 2010-09-22 20:35:11
We haven't had much luck getting people to enroll in those in the past, but we may try it again in the future.

Dsquared 2010-09-22 20:35:15
What is the recommed order of courses?

rrusczyk 2010-09-22 20:35:31
Essentially what you see on the schedule page:

rrusczyk 2010-09-22 20:35:32
http://www.artofproblemsolving.com/School/classlist.php

catlover114 2010-09-22 20:35:35
With Geometry, how do students post diagrams with their work?

rrusczyk 2010-09-22 20:36:17
On the message board, they can use geogebra (try clicking the Geogebra button when you make a post). For their Challenge Sets, they can use whatever they want, including hand-drawn. In class, the teacher provides all the necessary diagrams.

theorist2 2010-09-22 20:36:47
Are the message boards for problem series courses as busy as those for subject courses?

rrusczyk 2010-09-22 20:36:49
Depends on the course. Just like with the subject classes, the older the students, the less active the message boards, probably because older students have so many other time demands.

rrusczyk 2010-09-22 20:37:00
Are there any more questions about the courses?

Curtis 2010-09-22 20:37:31
I'm in 8th grade geometry, and have taken intro. o number theory, will intermediate number theory be to hard for me?

rrusczyk 2010-09-22 20:38:05
Hard to say. You could try the first two weeks, and then drop if you find it too hard. If you haven't gone through the counting class or book, that could be a good choice.

theorist2 2010-09-22 20:38:08
Do the problem series courses usually us new-mock or old -real test questions?

rrusczyk 2010-09-22 20:38:15
Mostly old test questions.

koek67 2010-09-22 20:38:25
I am in 9th grade taking honors Geometry. I have enrolled for intro geometry, will it be a good fit for me

rrusczyk 2010-09-22 20:38:36
Sure. It will make your school class very easy.

rrusczyk 2010-09-22 20:39:32
Thank you for attending the Math Jam! If you have any more questions, we can be reached at classes@artofproblemsolving.com. If you would like specific recommendations, you can email me at that address. Include your math background, including what classes you have taken and your goals in taking a course.

Qazmaz 2010-09-22 20:40:41
is this the end of the session?

rrusczyk 2010-09-22 20:40:48
Yes. See you next time!

LotharCollatz 2010-09-22 20:40:52
Thank you

theorist2 2010-09-22 20:40:52
Thank you.

theorist2 2010-09-22 20:40:52
This was very helpful and informative.

koek67 2010-09-22 20:40:52
thank you very much, I wish I had known about these courses before, I could have taken some classes during summer

rrusczyk 2010-09-22 20:40:58
We'll catch you next summer ;)

AoPS Classes Math Jam

Facilitator: Richard Rusczyk