2011 AIME I Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2011 AIME I.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Richard Rusczyk
rrusczyk
2011-03-19 19:02:53
Welcome to the 2011 AIME I Math Jam!
Welcome to the 2011 AIME I Math Jam!
rrusczyk
2011-03-19 19:02:58
I'm Richard Rusczyk, founder of AoPS, and I'll be leading our discussion tonight.
I'm Richard Rusczyk, founder of AoPS, and I'll be leading our discussion tonight.
rrusczyk
2011-03-19 19:03:01
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
rrusczyk
2011-03-19 19:03:07
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
rrusczyk
2011-03-19 19:03:15
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
rrusczyk
2011-03-19 19:03:26
There are a lot of students here! As I said, only (a very small fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only (a very small fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
rrusczyk
2011-03-19 19:03:46
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all! This Math Jam will be much more of a zoo than our usual classes.
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all! This Math Jam will be much more of a zoo than our usual classes.
rrusczyk
2011-03-19 19:04:03
We have an assistant to help us out tonight -- Miles Dillon Edwards. Miles is an alumnus of Canada/USA Mathcamp, the Research Science Institute, HCSSiM, and MOP. He is a top-25 scorer on the Putnam exam, and he was also a four-time USAMO qualifier, a two-time ARML high scorer, and a participant at Mathcounts nationals (representing Georgia). He discovered a new proof for Heron's formula in 2007. (You can find it in our Precalculus text!) He is currently studying math and cello performance at Indiana University. His username is Boy Soprano II.
We have an assistant to help us out tonight -- Miles Dillon Edwards. Miles is an alumnus of Canada/USA Mathcamp, the Research Science Institute, HCSSiM, and MOP. He is a top-25 scorer on the Putnam exam, and he was also a four-time USAMO qualifier, a two-time ARML high scorer, and a participant at Mathcounts nationals (representing Georgia). He discovered a new proof for Heron's formula in 2007. (You can find it in our Precalculus text!) He is currently studying math and cello performance at Indiana University. His username is Boy Soprano II.
Boy Soprano II
2011-03-19 19:04:13
Hello!
Hello!
rrusczyk
2011-03-19 19:04:35
He can answer questions by whispering to you or by opening a window with you to chat 1-on-1.
He can answer questions by whispering to you or by opening a window with you to chat 1-on-1.
rrusczyk
2011-03-19 19:04:45
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
apple.singer
2011-03-19 19:05:19
will we go through multiple solutions to some problems?
will we go through multiple solutions to some problems?
rrusczyk
2011-03-19 19:05:28
Yes, but not many. We do have 15 problems to cover!
Yes, but not many. We do have 15 problems to cover!
rrusczyk
2011-03-19 19:05:35
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test?
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test?
SuperNerd123
2011-03-19 19:06:05
#4
#4
hsm174
2011-03-19 19:06:05
10
10
calvinhobbesliker
2011-03-19 19:06:05
Number 9
Number 9
cwein3
2011-03-19 19:06:05
number 4
number 4
policecap
2011-03-19 19:06:05
#15
#15
daddy1cherry
2011-03-19 19:06:05
1
1
knowmath
2011-03-19 19:06:05
#8
#8
KingSmasher3
2011-03-19 19:06:05
8
8
hchen023
2011-03-19 19:06:05
Question 15
Question 15
hrithikguy
2011-03-19 19:06:05
#4 because it was so epic
#4 because it was so epic
inquisitivity
2011-03-19 19:06:05
#7
#7
tan90
2011-03-19 19:06:05
Number 6
Number 6
leekspeak
2011-03-19 19:06:05
5
5
policecap
2011-03-19 19:06:05
#12
#12
JSGandora
2011-03-19 19:06:05
number 7!
number 7!
pi091997
2011-03-19 19:06:05
1. the easiest one :D
1. the easiest one :D
admin25
2011-03-19 19:06:05
#1-it was the only one I could easily do.
#1-it was the only one I could easily do.
dlennon
2011-03-19 19:06:05
I liked problem 11.
I liked problem 11.
mathelete
2011-03-19 19:06:05
#11
#11
daddy1cherry
2011-03-19 19:06:05
The ones I could answer.
The ones I could answer.
willwang123
2011-03-19 19:06:05
Number 1
Number 1
apple.singer
2011-03-19 19:06:05
#5
#5
hrithikguy
2011-03-19 19:06:05
#4 because it was so epically hard!
#4 because it was so epically hard!
BOGTRO
2011-03-19 19:06:05
7 i guess
7 i guess
wtRiViaL
2011-03-19 19:06:05
not number 3
not number 3
.cpp
2011-03-19 19:06:05
Number 4.
Number 4.
crobogc
2011-03-19 19:06:05
#3, because of the graph
#3, because of the graph
rrusczyk
2011-03-19 19:06:12
A lot of different answers!
A lot of different answers!
rrusczyk
2011-03-19 19:06:26
Here's a question I'm guessing won't have many different answers:
Here's a question I'm guessing won't have many different answers:
rrusczyk
2011-03-19 19:06:28
OK, what was your least favorite problem?
OK, what was your least favorite problem?
leekspeak
2011-03-19 19:06:43
3
3
mhy123
2011-03-19 19:06:43
#4
#4
inquisitivity
2011-03-19 19:06:43
#3
#3
zazz4
2011-03-19 19:06:43
3
3
prophet886
2011-03-19 19:06:43
the same ones :)
the same ones :)
bojobo
2011-03-19 19:06:43
number 4
number 4
minirafa
2011-03-19 19:06:43
13
13
SuperNerd123
2011-03-19 19:06:43
#1
#1
agejiageji
2011-03-19 19:06:43
number 3
number 3
hrithikguy
2011-03-19 19:06:43
#4!! I hated that!!
#4!! I hated that!!
girishvar12
2011-03-19 19:06:43
#3
#3
jeff10
2011-03-19 19:06:43
4
4
wtRiViaL
2011-03-19 19:06:43
number 3 haha
number 3 haha
apple.singer
2011-03-19 19:06:43
#4
#4
cwein3
2011-03-19 19:06:43
3
3
mathelete
2011-03-19 19:06:43
#4
#4
sincostanseccsccot
2011-03-19 19:06:43
#1 I got it wrong
#1 I got it wrong
KingSmasher3
2011-03-19 19:06:43
definately 4
definately 4
willwang123
2011-03-19 19:06:43
All the other ones
All the other ones
minirafa
2011-03-19 19:06:43
13
13
JoeJack
2011-03-19 19:06:43
14
14
ahaanomegas
2011-03-19 19:06:43
None, all were pretty interesting
None, all were pretty interesting
DavidTong
2011-03-19 19:06:43
3
3
bojobo
2011-03-19 19:06:43
definitely
definitely
omega1
2011-03-19 19:06:43
number 7
number 7
hsm174
2011-03-19 19:06:43
num 5
num 5
vcez
2011-03-19 19:06:43
3/4, too hard
3/4, too hard
theone142857
2011-03-19 19:06:43
12
12
policecap
2011-03-19 19:06:43
7
7
calvinhobbesliker
2011-03-19 19:06:43
4 and 3
4 and 3
policecap
2011-03-19 19:06:43
#7
#7
rrusczyk
2011-03-19 19:06:56
I was guessing I'd see a lot of 3&4 on that one.
I was guessing I'd see a lot of 3&4 on that one.
rrusczyk
2011-03-19 19:07:01
Let's get to the problems.
Let's get to the problems.
rrusczyk
2011-03-19 19:07:06
At a couple points during the Math Jam, I will get thirsty or hungry, or my fingers will get tired, and I'll take a 1-2 minute break. Other than that, we will simply plow through all 15 problems.
At a couple points during the Math Jam, I will get thirsty or hungry, or my fingers will get tired, and I'll take a 1-2 minute break. Other than that, we will simply plow through all 15 problems.
rrusczyk
2011-03-19 19:07:17
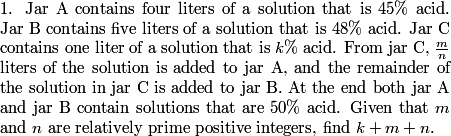
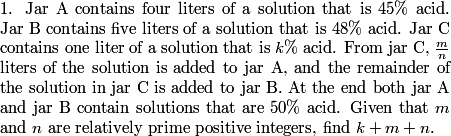
rrusczyk
2011-03-19 19:07:28
What do we find first?
What do we find first?
Ttocs45
2011-03-19 19:07:54
k
k
Kinata12
2011-03-19 19:07:54
k?
k?
.cpp
2011-03-19 19:07:54
Solve for k.
Solve for k.
willwang123
2011-03-19 19:07:54
k?
k?
vcez
2011-03-19 19:07:54
k
k
rrusczyk
2011-03-19 19:08:02
And how do we find k quickly
And how do we find k quickly
rrusczyk
2011-03-19 19:08:03
?
?
connaissance
2011-03-19 19:08:48
look at the acid before and after
look at the acid before and after
KingSmasher3
2011-03-19 19:08:49
set up an equation relating k with the final ratio of 50%
set up an equation relating k with the final ratio of 50%
.cpp
2011-03-19 19:08:49
There must be a total of 5 liters of acid.
There must be a total of 5 liters of acid.
JSGandora
2011-03-19 19:08:49
we see that the total amount of acid will be 5 liters so we just add up the acid from each jar to get 5 and then solve for k
we see that the total amount of acid will be 5 liters so we just add up the acid from each jar to get 5 and then solve for k
superpi83
2011-03-19 19:08:49
jar A has 1.8L of acid, jar B has 2.4L acid. we need a total of 5L acid so jar C must have 0.8L acid
jar A has 1.8L of acid, jar B has 2.4L acid. we need a total of 5L acid so jar C must have 0.8L acid
rrusczyk
2011-03-19 19:08:53
We can find k pretty quickly. We know that we have 10 liters total in the end, and that 5 liters of this total is acid.
We can find k pretty quickly. We know that we have 10 liters total in the end, and that 5 liters of this total is acid.
rrusczyk
2011-03-19 19:09:08
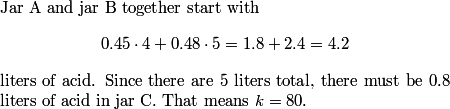
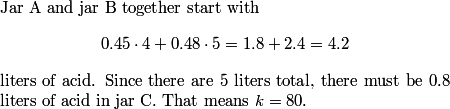
sincostanseccsccot
2011-03-19 19:09:16
k=80
k=80
rrusczyk
2011-03-19 19:09:18
Now, we must find the number of liters of jar C we add to jar A. Suppose we let this amount be t. Then what?
Now, we must find the number of liters of jar C we add to jar A. Suppose we let this amount be t. Then what?
rrusczyk
2011-03-19 19:10:36
There are a lot of ways to finish from here!
There are a lot of ways to finish from here!
BOGTRO
2011-03-19 19:10:41
1.8+4/5t=1/2(4+t)
1.8+4/5t=1/2(4+t)
superpi83
2011-03-19 19:10:41
1.8+0.8t=0.5(4+t)
1.8+0.8t=0.5(4+t)
.cpp
2011-03-19 19:10:41
Jar A must have 50% acid. .8t + .45(4) = 1/2 (t+4).
Jar A must have 50% acid. .8t + .45(4) = 1/2 (t+4).
Luminescence
2011-03-19 19:10:41
1.8 + .8t = .5(4 + t)
1.8 + .8t = .5(4 + t)
BOGTRO
2011-03-19 19:10:47
1.8+.8t=1/2(4+t)=2+.5t --> .3t=.2 --> t=2/3
1.8+.8t=1/2(4+t)=2+.5t --> .3t=.2 --> t=2/3
rrusczyk
2011-03-19 19:10:52
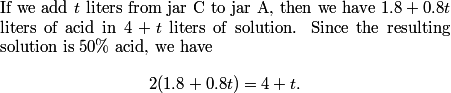
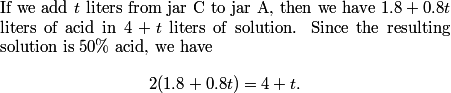
rrusczyk
2011-03-19 19:11:04
And what do we find?
And what do we find?
tiger21
2011-03-19 19:11:20
t=2/3
t=2/3
hrithikguy
2011-03-19 19:11:20
t = 2/3
t = 2/3
tiger21
2011-03-19 19:11:20
t=2/3
t=2/3
JSGandora
2011-03-19 19:11:20
t=2/3
t=2/3
KingSmasher3
2011-03-19 19:11:20
t=2/3
t=2/3
apple.singer
2011-03-19 19:11:26
t=2/3
t=2/3
centralbs
2011-03-19 19:11:26
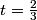
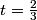
rrusczyk
2011-03-19 19:11:29
Rearranging this equation gives 0.6t = 0.4, so t = 2/3.
Rearranging this equation gives 0.6t = 0.4, so t = 2/3.
prezcoin
2011-03-19 19:11:43
k+m+n= 80+2+3= 85
k+m+n= 80+2+3= 85
j_f_c_w
2011-03-19 19:11:43
m+n+k=85
m+n+k=85
superpi83
2011-03-19 19:11:43
so the answer is 80+2+3=085
so the answer is 80+2+3=085
vcez
2011-03-19 19:11:43
thus our answer is 2+3+80=85
thus our answer is 2+3+80=85
.cpp
2011-03-19 19:11:43
Thus, k+m+n = 80+2+3 = 085.
Thus, k+m+n = 80+2+3 = 085.
rrusczyk
2011-03-19 19:11:47
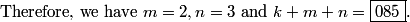
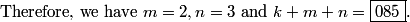
rrusczyk
2011-03-19 19:11:53
1 down. 14 to go.
1 down. 14 to go.
rrusczyk
2011-03-19 19:12:05
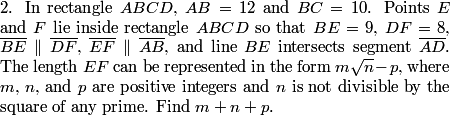
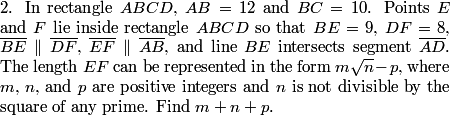
mhy123
2011-03-19 19:12:17
diagram
diagram
calvinhobbesliker
2011-03-19 19:12:17
Draw a picture
Draw a picture
rrusczyk
2011-03-19 19:12:20
We start with a picture:
We start with a picture:
rrusczyk
2011-03-19 19:12:24
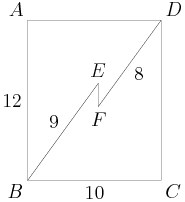

rrusczyk
2011-03-19 19:12:36
Any bright ideas?
Any bright ideas?
rrusczyk
2011-03-19 19:12:51
What should we build here?
What should we build here?
willwang123
2011-03-19 19:13:05
Draw triangles?
Draw triangles?
agejiageji
2011-03-19 19:13:05
a right triangle
a right triangle
jellymoop
2011-03-19 19:13:05
right triangle?
right triangle?
mhy123
2011-03-19 19:13:05
right triangles
right triangles
rrusczyk
2011-03-19 19:13:10
We have a rectangle. We want a length. We should build a right triangle. We should build a smart right triangle.
We have a rectangle. We want a length. We should build a right triangle. We should build a smart right triangle.
Kinata12
2011-03-19 19:13:56
Move ED upwards so that F is on E
Move ED upwards so that F is on E
Luminescence
2011-03-19 19:13:56
extend BE and FD
extend BE and FD
dlennon
2011-03-19 19:13:56
Extend BE and DF.
Extend BE and DF.
Ttocs45
2011-03-19 19:13:56
Extend BE so it meets CD
Extend BE so it meets CD
rrusczyk
2011-03-19 19:14:01
We extend BE to hit the extension of CD. This may look like magic, but it builds a right triangle in which we know two sides, and the third has the length we want as part of it:
We extend BE to hit the extension of CD. This may look like magic, but it builds a right triangle in which we know two sides, and the third has the length we want as part of it:
rrusczyk
2011-03-19 19:14:05
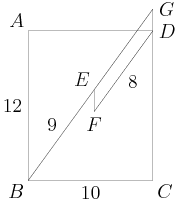

rrusczyk
2011-03-19 19:14:12
And just like that, we're done. Why?
And just like that, we're done. Why?
policecap
2011-03-19 19:14:50
GD=EF
GD=EF
zazz4
2011-03-19 19:14:50
CG-CD=the answer
CG-CD=the answer
hrithikguy
2011-03-19 19:14:50
GD = EF
GD = EF
prezcoin
2011-03-19 19:14:50
EF=GD
EF=GD
wtRiViaL
2011-03-19 19:14:50
now BG=17, BC=10, and you can find GC. THen you subtract 12 to get GD=EF
now BG=17, BC=10, and you can find GC. THen you subtract 12 to get GD=EF
SuperNerd123
2011-03-19 19:14:50
Because GD=EF
Because GD=EF
girishvar12
2011-03-19 19:14:50
pythogeoren theorem
pythogeoren theorem
Luminescence
2011-03-19 19:14:50
pythagorean theorem!
pythagorean theorem!
BOGTRO
2011-03-19 19:14:50
right triangle, 10^2+(x+12)^2=(9+8)^2
right triangle, 10^2+(x+12)^2=(9+8)^2
Kinata12
2011-03-19 19:14:50
10^2+(12+x)^2=17^2. Easy to solve
10^2+(12+x)^2=17^2. Easy to solve
tekgeek
2011-03-19 19:14:50
EG=FD=8
EG=FD=8
xD13G0x
2011-03-19 19:14:57
we can calculate GC, we know CD so we know GD=EF
we can calculate GC, we know CD so we know GD=EF
rrusczyk
2011-03-19 19:15:01
EFDG is a parallelogram, so EG = FD = 8 and GD = EF. Now we just have to find GD.
EFDG is a parallelogram, so EG = FD = 8 and GD = EF. Now we just have to find GD.
stickfigure
2011-03-19 19:15:17
since GD = EF, we can do sqrt(17^2-10^2) to find GC and subtract away 12 to get the answer
since GD = EF, we can do sqrt(17^2-10^2) to find GC and subtract away 12 to get the answer
.cpp
2011-03-19 19:15:17
GC = sqrt(289-100) = sqrt(189) by Pythagorean theorem, so the answer is 3sqrt21 - 12.
GC = sqrt(289-100) = sqrt(189) by Pythagorean theorem, so the answer is 3sqrt21 - 12.
vcez
2011-03-19 19:15:22
3sqrt21-10
3sqrt21-10
policecap
2011-03-19 19:15:26
sqrt{189}-12
sqrt{189}-12
rrusczyk
2011-03-19 19:15:32
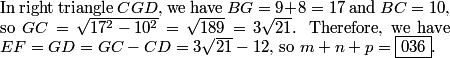
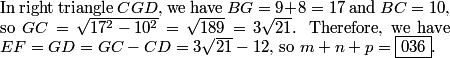
apple.singer
2011-03-19 19:15:37
and 3+21+12=36
and 3+21+12=36
ahaanomegas
2011-03-19 19:15:37
Answer = 3 + 21 + 12 = 3 + 33 = 036
Answer = 3 + 21 + 12 = 3 + 33 = 036
rrusczyk
2011-03-19 19:15:54
2 down. The next one is a bit of a monster.
2 down. The next one is a bit of a monster.
rrusczyk
2011-03-19 19:16:05
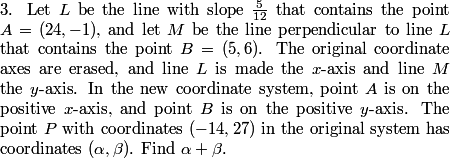
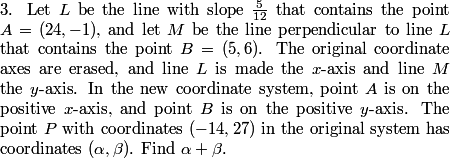
rrusczyk
2011-03-19 19:16:17
This problem gave a lot of people problems on the test, so we're going to go through 3 solutions here with pretty different fundamental approaches. One is going to be grind-it-out-analytic geometry solution that requires knowing a somewhat obscure formula. One is going to be an elegant linear algebra approach that requires knowing some pretty advanced (and cool) math. Both of these require knowledge that we think is too obscure for a #3 on the AIME (but the first is lamentably the official solution). So, we're going to also find a solution using very basic geometry.
This problem gave a lot of people problems on the test, so we're going to go through 3 solutions here with pretty different fundamental approaches. One is going to be grind-it-out-analytic geometry solution that requires knowing a somewhat obscure formula. One is going to be an elegant linear algebra approach that requires knowing some pretty advanced (and cool) math. Both of these require knowledge that we think is too obscure for a #3 on the AIME (but the first is lamentably the official solution). So, we're going to also find a solution using very basic geometry.
rrusczyk
2011-03-19 19:16:40
All three solutions start with the same insight. What are we really looking for when we say we want the coordinates of P with respect to the new axes.
All three solutions start with the same insight. What are we really looking for when we say we want the coordinates of P with respect to the new axes.
leekspeak
2011-03-19 19:17:05
distance to each line
distance to each line
tan90
2011-03-19 19:17:05
The distance from P to the lines.
The distance from P to the lines.
policecap
2011-03-19 19:17:05
the lengtsh of the perpendiculars to the axes
the lengtsh of the perpendiculars to the axes
Luminescence
2011-03-19 19:17:05
the distance from P to the two lines
the distance from P to the two lines
calvinhobbesliker
2011-03-19 19:17:05
We want the distance from P to each of the 2 lines
We want the distance from P to each of the 2 lines
wtRiViaL
2011-03-19 19:17:05
distance from point P to lines L and M
distance from point P to lines L and M
rrusczyk
2011-03-19 19:17:10
The coordinates of a point in any rectangular coordinate system are simply the signed distances to the axes of the coordinate system (the "signed" means points on one side of an axis have a negative coordinate and those on the other side have a positive coordinate.)
The coordinates of a point in any rectangular coordinate system are simply the signed distances to the axes of the coordinate system (the "signed" means points on one side of an axis have a negative coordinate and those on the other side have a positive coordinate.)
rrusczyk
2011-03-19 19:17:19
To find the coordinates of (-14,27) with respect to our new axes, we just figure out how far (-14,27) is from each axis. Again, what do we have to be careful about?
To find the coordinates of (-14,27) with respect to our new axes, we just figure out how far (-14,27) is from each axis. Again, what do we have to be careful about?
leekspeak
2011-03-19 19:17:28
signs
signs
AceOfDiamonds
2011-03-19 19:17:28
signs
signs
SuperNerd123
2011-03-19 19:17:28
signs
signs
mhy123
2011-03-19 19:17:30
signs?
signs?
numberwiz
2011-03-19 19:17:37
sign
sign
PiquantPeppers
2011-03-19 19:17:37
signs
signs
ahaanomegas
2011-03-19 19:17:37
Signs*
Signs*
ahaanomegas
2011-03-19 19:17:39
Sings
Sings
rrusczyk
2011-03-19 19:17:58
It's OK to sing. Well, maybe OK for Boy Soprano to sing. You don't want me to sing.
It's OK to sing. Well, maybe OK for Boy Soprano to sing. You don't want me to sing.
rrusczyk
2011-03-19 19:18:06
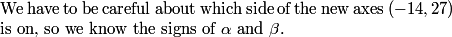
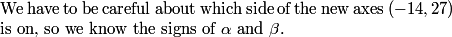
rrusczyk
2011-03-19 19:18:13
All right, we have a plan. Let's execute it carefully and make sure we don't make any mistakes.
All right, we have a plan. Let's execute it carefully and make sure we don't make any mistakes.
rrusczyk
2011-03-19 19:18:16
First, we'll do the grimy analytic geometry solution.
First, we'll do the grimy analytic geometry solution.
calvinhobbesliker
2011-03-19 19:18:21
Can we use distance from point to line formula?
Can we use distance from point to line formula?
jellymoop
2011-03-19 19:18:27
distance from a point to a line
distance from a point to a line
rrusczyk
2011-03-19 19:18:40
First line L. How do we figure out how far (-14,27) is from L?
First line L. How do we figure out how far (-14,27) is from L?
tan90
2011-03-19 19:19:04
Find the equation of L first.
Find the equation of L first.
hrithikguy
2011-03-19 19:19:04
find the equation of L
find the equation of L
Jasmine8925
2011-03-19 19:19:04
first let's find line L
first let's find line L
rrusczyk
2011-03-19 19:19:11
We first figure out an equation for L in the original coordinate system. What is it?
We first figure out an equation for L in the original coordinate system. What is it?
leekspeak
2011-03-19 19:19:40
L is y=(5/12)x-11
L is y=(5/12)x-11
jsani0102
2011-03-19 19:19:40
L=5/12x-11
L=5/12x-11
hrithikguy
2011-03-19 19:19:40
y = 5/12 x - 11
y = 5/12 x - 11
apple.singer
2011-03-19 19:19:40
y=5/12x-11
y=5/12x-11
policecap
2011-03-19 19:19:40
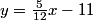
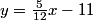
professordad
2011-03-19 19:19:40
y=5x/12-11
y=5x/12-11
hchen023
2011-03-19 19:19:40
y + 1 = (5/12)(x - 24)
y + 1 = (5/12)(x - 24)
rrusczyk
2011-03-19 19:19:44
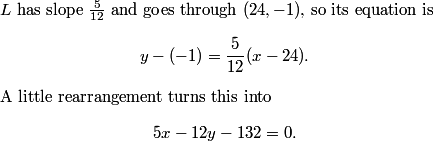
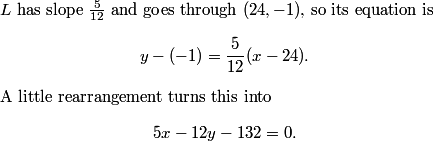
rrusczyk
2011-03-19 19:19:47
And how do figure out where (-14, 27) is with respect to this line?
And how do figure out where (-14, 27) is with respect to this line?
anonymous0
2011-03-19 19:20:02
you use magic
you use magic
rrusczyk
2011-03-19 19:20:06
Pretty close.
Pretty close.
hrithikguy
2011-03-19 19:20:09
iti s above line L
iti s above line L
rrusczyk
2011-03-19 19:20:19
So, we know that the coordinate is positive.
So, we know that the coordinate is positive.
.cpp
2011-03-19 19:20:21
Use the |Ax+By+C|/sqrt(A^2+B^2) formula.
Use the |Ax+By+C|/sqrt(A^2+B^2) formula.
jellymoop
2011-03-19 19:20:25
the brutal formula!
the brutal formula!
rrusczyk
2011-03-19 19:20:40
First, we note that this point is above the line. The y-coordinate of the point on the line with x = -14 is the solution to 5(-14) - 12y -132 =0. The solution to this equation is clearly way less than 27. So, (-14,27) is "above" this line in our new coordinate system.
First, we note that this point is above the line. The y-coordinate of the point on the line with x = -14 is the solution to 5(-14) - 12y -132 =0. The solution to this equation is clearly way less than 27. So, (-14,27) is "above" this line in our new coordinate system.
rrusczyk
2011-03-19 19:20:43
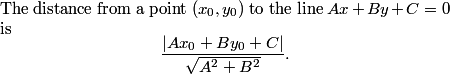
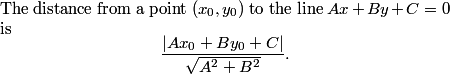
rrusczyk
2011-03-19 19:20:51
This is the grimy formula people are talking about.
This is the grimy formula people are talking about.
rrusczyk
2011-03-19 19:21:12
This is why I was not very happy to see this at #3, and that this was the official solution.
This is why I was not very happy to see this at #3, and that this was the official solution.
SuperNerd123
2011-03-19 19:21:19
How is that derived?
How is that derived?
rrusczyk
2011-03-19 19:21:33
It's proved in a couple of our books :) A nice way is with vectors.
It's proved in a couple of our books :) A nice way is with vectors.
GoldenFrog1618
2011-03-19 19:21:35
when did the AMC assume everyone had knowledge of that?
when did the AMC assume everyone had knowledge of that?
mentalgenius
2011-03-19 19:21:49
which books?
which books?
rrusczyk
2011-03-19 19:21:57
Precalculus, and possibly Intro Geometry.
Precalculus, and possibly Intro Geometry.
rrusczyk
2011-03-19 19:22:09
Fair question, GoldenFrog. Now, let's finish the problem with this formula.
Fair question, GoldenFrog. Now, let's finish the problem with this formula.
rrusczyk
2011-03-19 19:22:16
What does this give us for the distance?
What does this give us for the distance?
tiger21
2011-03-19 19:23:14
526/13
526/13
professordad
2011-03-19 19:23:14
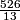
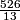
dlennon
2011-03-19 19:23:33
526/13
526/13
paddock1570
2011-03-19 19:23:33
526/13
526/13
ahaanomegas
2011-03-19 19:23:33
526/13
526/13
rrusczyk
2011-03-19 19:23:43
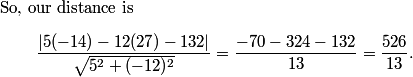
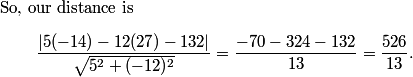
rrusczyk
2011-03-19 19:23:51
Since the point is 526/13 above our new x-axis (line L), its y-coordinate is 526/13.
Since the point is 526/13 above our new x-axis (line L), its y-coordinate is 526/13.
rrusczyk
2011-03-19 19:23:54
OK, on to line M. What is the equation of line M?
OK, on to line M. What is the equation of line M?
jeff10
2011-03-19 19:24:25
y=-12x/5+18
y=-12x/5+18
apple.singer
2011-03-19 19:24:25
y=-12/5x+18
y=-12/5x+18
hrithikguy
2011-03-19 19:24:25
y = -12/5 x + 18
y = -12/5 x + 18
tekgeek
2011-03-19 19:24:25
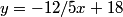
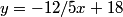
hrithikguy
2011-03-19 19:24:25
y = -12/5 x + 18
y = -12/5 x + 18
professordad
2011-03-19 19:24:25
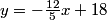
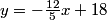
rrusczyk
2011-03-19 19:24:28
Since line M is perpendicular to L, it has slope -1/(5/12) = -12/5.
Since line M is perpendicular to L, it has slope -1/(5/12) = -12/5.
rrusczyk
2011-03-19 19:24:32
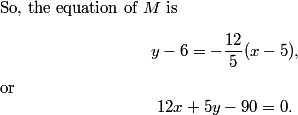
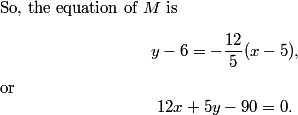
rrusczyk
2011-03-19 19:24:44
What do we have to be careful about here?
What do we have to be careful about here?
zazz4
2011-03-19 19:24:55
signs
signs
hrithikguy
2011-03-19 19:24:55
the signs!!
the signs!!
sindennisz
2011-03-19 19:24:55
SIgns
SIgns
anonymous0
2011-03-19 19:24:55
signs
signs
calvinhobbesliker
2011-03-19 19:24:55
Signs
Signs
vcez
2011-03-19 19:24:55
signs'
signs'
mentalgenius
2011-03-19 19:24:58
signs
signs
JSGandora
2011-03-19 19:24:58
signs
signs
prezcoin
2011-03-19 19:24:58
the sign is negative
the sign is negative
policecap
2011-03-19 19:24:58
sings
sings
jzz
2011-03-19 19:24:58
signs?
signs?
rrusczyk
2011-03-19 19:25:01
Here, we have to be a little careful when figuring out where (-14,27) is with respect to this line. The point on line M with x = -14 in our original coordinate system has a y-coordinate that is the solution to 12(-14) + 5y - 90 = 0. The solution to this equation is greater than 50, so M passes above (14,-27) is our original coordinate system. That means that when we make M our y-axis in the new coordinate system, (-14,27) is to the left of our y-axis. In other words, its x-coordinate in the new system is negative.
Here, we have to be a little careful when figuring out where (-14,27) is with respect to this line. The point on line M with x = -14 in our original coordinate system has a y-coordinate that is the solution to 12(-14) + 5y - 90 = 0. The solution to this equation is greater than 50, so M passes above (14,-27) is our original coordinate system. That means that when we make M our y-axis in the new coordinate system, (-14,27) is to the left of our y-axis. In other words, its x-coordinate in the new system is negative.
rrusczyk
2011-03-19 19:25:32
How far is the point from M?
How far is the point from M?
KingSmasher3
2011-03-19 19:25:51
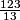
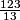
tiger21
2011-03-19 19:25:51
123/13
123/13
tekgeek
2011-03-19 19:25:51
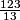
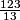
superpi83
2011-03-19 19:25:51
123/13
123/13
tan90
2011-03-19 19:25:58
123/13
123/13
dlennon
2011-03-19 19:25:58
123/13
123/13
vcez
2011-03-19 19:25:58
123/13
123/13
superpi83
2011-03-19 19:26:00
well signs doesnt really matter much in this problem because if you add both instead of subtracting one from the other you get a non-integral answer...
well signs doesnt really matter much in this problem because if you add both instead of subtracting one from the other you get a non-integral answer...
rrusczyk
2011-03-19 19:26:04
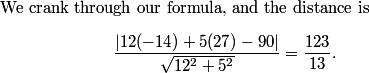
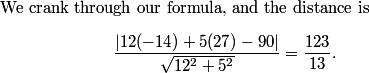
rrusczyk
2011-03-19 19:26:09
Since the point is to the left of our new y-axis (line m), the new x-coordinate of the point is -123/13. (This would have been a particularly evil problem if taking the positive value here had made the sum of the new coordinates an integer.)
Since the point is to the left of our new y-axis (line m), the new x-coordinate of the point is -123/13. (This would have been a particularly evil problem if taking the positive value here had made the sum of the new coordinates an integer.)
rrusczyk
2011-03-19 19:26:16
And our answer is?
And our answer is?
theone142857
2011-03-19 19:26:36
31
31
vcez
2011-03-19 19:26:36
31
31
policecap
2011-03-19 19:26:36
31
31
KingSmasher3
2011-03-19 19:26:36
031
031
JSGandora
2011-03-19 19:26:36
031
031
.cpp
2011-03-19 19:26:36
Adding (watching signs), we get (526-123)/13 = 031.
Adding (watching signs), we get (526-123)/13 = 031.
gh625
2011-03-19 19:26:36
031
031
mentalgenius
2011-03-19 19:26:36
31
31
tiger21
2011-03-19 19:26:36
31
31
policecap
2011-03-19 19:26:36


mhy123
2011-03-19 19:26:40
31
31
PiquantPeppers
2011-03-19 19:26:40
31
31
omega1
2011-03-19 19:26:40
31
31
tekgeek
2011-03-19 19:26:40


vcez
2011-03-19 19:26:40
031
031
professordad
2011-03-19 19:26:40


rrusczyk
2011-03-19 19:26:43
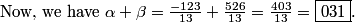
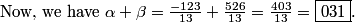
rrusczyk
2011-03-19 19:26:47
All right, that wasn't much fun. Let's try to do something a little more elegant.
All right, that wasn't much fun. Let's try to do something a little more elegant.
rrusczyk
2011-03-19 19:26:52
We want the distance from P to the line through A.
We want the distance from P to the line through A.
rrusczyk
2011-03-19 19:26:58


rrusczyk
2011-03-19 19:27:01
What else do we want to add to this diagram?
What else do we want to add to this diagram?
pi091997
2011-03-19 19:27:15
perp
perp
hrithikguy
2011-03-19 19:27:15
a perp from P to line A
a perp from P to line A
vcez
2011-03-19 19:27:15
a perpendicular line
a perpendicular line
numberwiz
2011-03-19 19:27:15
perp. form p to a
perp. form p to a
professordad
2011-03-19 19:27:15
perpendicular line from P to the line through A
perpendicular line from P to the line through A
GoldenFrog1618
2011-03-19 19:27:15
foot of P to A
foot of P to A
AlphaMath1
2011-03-19 19:27:15
perpendicular from P to A
perpendicular from P to A
rrusczyk
2011-03-19 19:27:21
We add in a perpendicular from P to the line, and we go ahead and draw PA. Since we know P and A, we can figure out stuff about PA if we need to.
We add in a perpendicular from P to the line, and we go ahead and draw PA. Since we know P and A, we can figure out stuff about PA if we need to.
rrusczyk
2011-03-19 19:27:25
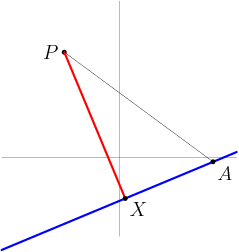

rrusczyk
2011-03-19 19:27:32
Now, for those of you who have some advanced experience with vectors, this sort of thing should look familiar. Vector XP is the projection of vector AP onto the vector normal to the blue line. (If that sentence was gibberish to you, it's OK to check out for a few minutes while we finish this solution. In the meantime, you can think about where you might learn such cool stuff: http://www.artofproblemsolving.com/Store/viewitem.php?item=precalc)
Now, for those of you who have some advanced experience with vectors, this sort of thing should look familiar. Vector XP is the projection of vector AP onto the vector normal to the blue line. (If that sentence was gibberish to you, it's OK to check out for a few minutes while we finish this solution. In the meantime, you can think about where you might learn such cool stuff: http://www.artofproblemsolving.com/Store/viewitem.php?item=precalc)
rrusczyk
2011-03-19 19:28:06
What is a vector normal to the blue line? (That is, tell me the components of a vector that is normal to the blue line.)
What is a vector normal to the blue line? (That is, tell me the components of a vector that is normal to the blue line.)
willwang123
2011-03-19 19:28:10
link doesn't work
link doesn't work
bulutcocuk
2011-03-19 19:28:10
parenthesis in the url :P
parenthesis in the url :P
rrusczyk
2011-03-19 19:28:27
Thank you for helping me advertise :)
Thank you for helping me advertise :)
Jasmine8925
2011-03-19 19:28:29
normal to means perpendicular to?
normal to means perpendicular to?
rrusczyk
2011-03-19 19:28:32
Yes.
Yes.
JSGandora
2011-03-19 19:28:54
PX
PX
centralbs
2011-03-19 19:28:54
Vector XP
Vector XP
rrusczyk
2011-03-19 19:28:59
I'm looking for numbers here.
I'm looking for numbers here.
rrusczyk
2011-03-19 19:29:11
Is (2 1) perpendicular to the blue line?
Is (2 1) perpendicular to the blue line?
anonymous0
2011-03-19 19:29:22
no
no
gh625
2011-03-19 19:29:22
No
No
rrusczyk
2011-03-19 19:29:27
Right. What is?
Right. What is?
policecap
2011-03-19 19:29:39
no, <-5,12> is
no, <-5,12> is
Potential5
2011-03-19 19:29:39
(5, -12)
(5, -12)
carmelninja
2011-03-19 19:29:39
<5, -12>
<5, -12>
gh625
2011-03-19 19:29:39
(-5,12)
(-5,12)
policecap
2011-03-19 19:29:41
(-5,12)
(-5,12)
rrusczyk
2011-03-19 19:29:45


rrusczyk
2011-03-19 19:29:56
And what is vector AP?
And what is vector AP?
rrusczyk
2011-03-19 19:30:01
(The vector from A to P?)
(The vector from A to P?)
GoldenFrog1618
2011-03-19 19:30:41
(-38,28)
(-38,28)
gh625
2011-03-19 19:30:41
(-38,28)
(-38,28)
rrusczyk
2011-03-19 19:30:45
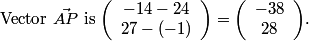
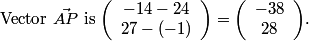
rrusczyk
2011-03-19 19:30:54
And now what do we want to do?
And now what do we want to do?
AceOfDiamonds
2011-03-19 19:31:18
fancy vector thing you were talking about earlier
fancy vector thing you were talking about earlier
SuperNerd123
2011-03-19 19:31:18
Use the projection formula (Express the cosine as the dot product)
Use the projection formula (Express the cosine as the dot product)
rrusczyk
2011-03-19 19:31:28
Exactly, here's where we use a projection.
Exactly, here's where we use a projection.
rrusczyk
2011-03-19 19:31:32


rrusczyk
2011-03-19 19:31:57
This is the super fancy thing that you have to know some pretty advanced linear algebra (vector math) to know. (It's in the Precalculus book, of course!)
This is the super fancy thing that you have to know some pretty advanced linear algebra (vector math) to know. (It's in the Precalculus book, of course!)
ahaanomegas
2011-03-19 19:32:03
When you say || n ||, do you mean |n|?
When you say || n ||, do you mean |n|?
rrusczyk
2011-03-19 19:32:07
Yes.
Yes.
rrusczyk
2011-03-19 19:32:14
Now, we crank through the computation.
Now, we crank through the computation.
rrusczyk
2011-03-19 19:32:18
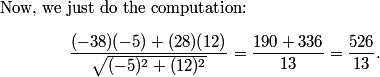
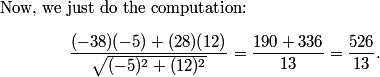
PiquantPeppers
2011-03-19 19:32:32
beast
beast
rrusczyk
2011-03-19 19:32:38
And that's all there is to it with this approach!
And that's all there is to it with this approach!
GoldenFrog1618
2011-03-19 19:32:43
this looks the same as above
this looks the same as above
hrithikguy
2011-03-19 19:32:43
this was basically the same formula, right?
this was basically the same formula, right?
rrusczyk
2011-03-19 19:33:01
Exactly! The distance from a point to a line formula can be proved with this same machinery.
Exactly! The distance from a point to a line formula can be proved with this same machinery.
rrusczyk
2011-03-19 19:33:15
With this approach, though, we didn't have to mess around with equations of lines and all that.
With this approach, though, we didn't have to mess around with equations of lines and all that.
rrusczyk
2011-03-19 19:33:24
Computationally, this way is a good deal faster.
Computationally, this way is a good deal faster.
rrusczyk
2011-03-19 19:33:32
But it requires knowing some very fancy stuff.
But it requires knowing some very fancy stuff.
rrusczyk
2011-03-19 19:33:38
Now, here's a good question:
Now, here's a good question:
mentalgenius
2011-03-19 19:33:41
Is there an easier way to do this problem?
Is there an easier way to do this problem?
rrusczyk
2011-03-19 19:34:01
We have seen two solutions that require knowing either advanced math or obscure formulas.
We have seen two solutions that require knowing either advanced math or obscure formulas.
policecap
2011-03-19 19:34:29
is there a solution with rotation?
is there a solution with rotation?
rrusczyk
2011-03-19 19:34:31
Some of you have mentioned using rotation of axes. That works, but that's pretty advanced, too (and you can do it pretty quickly with a rotation matrix!)
Some of you have mentioned using rotation of axes. That works, but that's pretty advanced, too (and you can do it pretty quickly with a rotation matrix!)
.cpp
2011-03-19 19:34:33
Now, let's just use normal geometry.
Now, let's just use normal geometry.
rrusczyk
2011-03-19 19:34:42
OK, let's try that.
OK, let's try that.
rrusczyk
2011-03-19 19:34:46
Let's see a solution that doesn't require any fancy machinery: just good old middle school geometry.
Let's see a solution that doesn't require any fancy machinery: just good old middle school geometry.
rrusczyk
2011-03-19 19:34:52
We start with the target. We want the distance from P to the blue line, and we know where P and A are:
We start with the target. We want the distance from P to the blue line, and we know where P and A are:
rrusczyk
2011-03-19 19:34:56
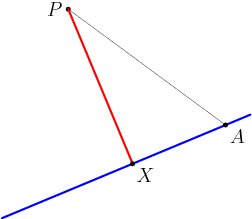

rrusczyk
2011-03-19 19:35:17
Notice that I've removed the axes. We're not going to write any equations of lines here. I want to find a purely geometric solution. What sort of distances do we know besides the distance from P to A?
Notice that I've removed the axes. We're not going to write any equations of lines here. I want to find a purely geometric solution. What sort of distances do we know besides the distance from P to A?
rrusczyk
2011-03-19 19:35:41
No distance formula. No nothing.
No distance formula. No nothing.
rrusczyk
2011-03-19 19:35:45
What do we know?
What do we know?
rrusczyk
2011-03-19 19:35:58
What do the coordinates tell us about P relative to A?
What do the coordinates tell us about P relative to A?
connaissance
2011-03-19 19:36:03
we know the differences between x-coordinates
we know the differences between x-coordinates
rrusczyk
2011-03-19 19:36:12
We know the horizontal distance and vertical distance from P to A. That is, we can draw a rectangle with P and A at opposite vertices such that the sides are parallel to the old axes. From the coordinates we are given for P and A, we know that the rectangle's dimensions are 38 and 28.
We know the horizontal distance and vertical distance from P to A. That is, we can draw a rectangle with P and A at opposite vertices such that the sides are parallel to the old axes. From the coordinates we are given for P and A, we know that the rectangle's dimensions are 38 and 28.
rrusczyk
2011-03-19 19:36:23


ahaanomegas
2011-03-19 19:36:44
How did we get 28 and 38, sorry!
How did we get 28 and 38, sorry!
rrusczyk
2011-03-19 19:37:01
38 is the difference in x-coordinates, 28 the difference in y coordinates
38 is the difference in x-coordinates, 28 the difference in y coordinates
hrithikguy
2011-03-19 19:37:10
i spy similar triangles!
i spy similar triangles!
Jasmine8925
2011-03-19 19:37:11
i see similar triangles
i see similar triangles
rrusczyk
2011-03-19 19:37:26
We draw in this rectangle, and we extend the sides of the rectangle to hit the blue lines because we like right triangles.
We draw in this rectangle, and we extend the sides of the rectangle to hit the blue lines because we like right triangles.
rrusczyk
2011-03-19 19:37:40
We particularly like these because they are all sorts of similar.
We particularly like these because they are all sorts of similar.
rrusczyk
2011-03-19 19:37:50
What more do we know about all these similar right triangles?
What more do we know about all these similar right triangles?
AlphaMath1
2011-03-19 19:38:10
5-12-13 right triangles
5-12-13 right triangles
professordad
2011-03-19 19:38:10
they're similar to 5-12-13 triangles
they're similar to 5-12-13 triangles
Kinata12
2011-03-19 19:38:13
The ratios of their sides.
The ratios of their sides.
Ttocs45
2011-03-19 19:38:13
Their leg ratio is 5 to 12 since the slope of the line is 5/12
Their leg ratio is 5 to 12 since the slope of the line is 5/12
rrusczyk
2011-03-19 19:38:17
These are 5-12-13 right triangles, from the given slope of the blue line. In fact, we have a bunch of similar 5-12-13 right triangles.
These are 5-12-13 right triangles, from the given slope of the blue line. In fact, we have a bunch of similar 5-12-13 right triangles.
rrusczyk
2011-03-19 19:38:27
We want PX. What length will allow us to get PX fastest?
We want PX. What length will allow us to get PX fastest?
GoldenFrog1618
2011-03-19 19:39:01
PK
PK
dlennon
2011-03-19 19:39:01
PK
PK
policecap
2011-03-19 19:39:10
PK
PK
ahaanomegas
2011-03-19 19:39:11
PK
PK
rrusczyk
2011-03-19 19:39:24
Since PKX is a 5-12-13 right triangle, we have PX = (12/13)(PK). And how do we get PK?
Since PKX is a 5-12-13 right triangle, we have PX = (12/13)(PK). And how do we get PK?
theone142857
2011-03-19 19:39:52
28+NK
28+NK
mhy123
2011-03-19 19:39:52
PN + NK
PN + NK
rrusczyk
2011-03-19 19:39:57
And how do we get NK?
And how do we get NK?
policecap
2011-03-19 19:40:05
28+38*5/12
28+38*5/12
.cpp
2011-03-19 19:40:05
NK = 5/12 (PM), so PK= 5/12(38) + 28.
NK = 5/12 (PM), so PK= 5/12(38) + 28.
AlphaMath1
2011-03-19 19:40:05
Find NK using the same 5-12-13 ratio in Triangle NAK
Find NK using the same 5-12-13 ratio in Triangle NAK
theone142857
2011-03-19 19:40:05
28+38*5/12
28+38*5/12
rrusczyk
2011-03-19 19:40:11
We find NK from 5-12-13 right triangle ANK. We have AN = PM = 38, so NK = (5/12)(38) = (5/6)(19).
We find NK from 5-12-13 right triangle ANK. We have AN = PM = 38, so NK = (5/12)(38) = (5/6)(19).
rrusczyk
2011-03-19 19:40:19
And now we compute.
And now we compute.
rrusczyk
2011-03-19 19:40:23
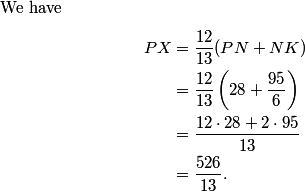
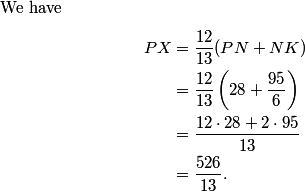
dlennon
2011-03-19 19:40:34
Same number
Same number
rrusczyk
2011-03-19 19:40:41
Phew! We didn't make a mistake.
Phew! We didn't make a mistake.
rrusczyk
2011-03-19 19:40:48
Tada! And we can do the same thing for the other coordinate. Because we still have 12 more problems to go, I'll leave that for you to work through for practice!
Tada! And we can do the same thing for the other coordinate. Because we still have 12 more problems to go, I'll leave that for you to work through for practice!
ahaanomegas
2011-03-19 19:40:54
That's nice!
That's nice!
bojobo
2011-03-19 19:40:54
the best solution
the best solution
rrusczyk
2011-03-19 19:40:57
:)
:)
flamingmath
2011-03-19 19:40:59
Could we have solved this with graph paper and a ruler?
Could we have solved this with graph paper and a ruler?
rrusczyk
2011-03-19 19:41:03
YES!
YES!
rrusczyk
2011-03-19 19:41:08
But it is very tricky how.
But it is very tricky how.
rrusczyk
2011-03-19 19:41:17
Your ruler is not going to tell you 526/13.
Your ruler is not going to tell you 526/13.
rrusczyk
2011-03-19 19:41:32
But there is a way to get a line with length 31 in the problem that you could measure!!
But there is a way to get a line with length 31 in the problem that you could measure!!
GoldenFrog1618
2011-03-19 19:41:41
who doesn't have a 1/13th inch ruler?
who doesn't have a 1/13th inch ruler?
rrusczyk
2011-03-19 19:41:44
:)
:)
numberwiz
2011-03-19 19:41:46
Where?
Where?
rrusczyk
2011-03-19 19:42:06
I'll tell you how, but you will have to figure out why it works.
I'll tell you how, but you will have to figure out why it works.
rrusczyk
2011-03-19 19:42:12
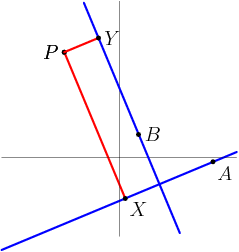

rrusczyk
2011-03-19 19:42:24
The blue lines are the new axes.
The blue lines are the new axes.
rrusczyk
2011-03-19 19:42:44
Draw a line through P that makes a 45 degree angle with both of the positive parts of the blue axes.
Draw a line through P that makes a 45 degree angle with both of the positive parts of the blue axes.
rrusczyk
2011-03-19 19:43:00
Let T be the point where that line hits one of the axes.
Let T be the point where that line hits one of the axes.
rrusczyk
2011-03-19 19:43:13
Think about the distance between T and the new origin!
Think about the distance between T and the new origin!
JSGandora
2011-03-19 19:43:30
clever
clever
rrusczyk
2011-03-19 19:43:51
If you find a quick solution with that approach, let me know. I so wanted that to lead to a nice solution!
If you find a quick solution with that approach, let me know. I so wanted that to lead to a nice solution!
rrusczyk
2011-03-19 19:44:00
Anyway, enough about that problem.
Anyway, enough about that problem.
rrusczyk
2011-03-19 19:44:11
If you still have questions about it, ask on the message board about it.
If you still have questions about it, ask on the message board about it.
AlphaMath1
2011-03-19 19:44:14
it's 31 because subtracting TY is the same thing as subtracting PY
it's 31 because subtracting TY is the same thing as subtracting PY
numberwiz
2011-03-19 19:44:15
Have you found that sol?
Have you found that sol?
rrusczyk
2011-03-19 19:44:20
Not yet :(
Not yet :(
mhy123
2011-03-19 19:44:29
oh oh #4
oh oh #4
rrusczyk
2011-03-19 19:44:32


rrusczyk
2011-03-19 19:44:39
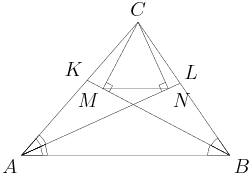

rrusczyk
2011-03-19 19:44:52
(If you drew your diagram with a straightedge and compass, then you would have a huge clue right away -- MN just plain looks parallel to AB.)
(If you drew your diagram with a straightedge and compass, then you would have a huge clue right away -- MN just plain looks parallel to AB.)
rrusczyk
2011-03-19 19:45:27
Even if you didn't, you have a couple right triangles sitting there, and equal angles from the angle bisectors. What do these just beg you to do?
Even if you didn't, you have a couple right triangles sitting there, and equal angles from the angle bisectors. What do these just beg you to do?
calvinhobbesliker
2011-03-19 19:45:44
Extend the perpendiculars
Extend the perpendiculars
vcez
2011-03-19 19:45:44
extend the perpendiculars
extend the perpendiculars
rrusczyk
2011-03-19 19:45:48
They just plain want you to continue CM and CN, since you know you'll get nice pretty congruent right triangles.
They just plain want you to continue CM and CN, since you know you'll get nice pretty congruent right triangles.
.cpp
2011-03-19 19:45:59
Extend CM and CN to intersect line AB.
Extend CM and CN to intersect line AB.
rrusczyk
2011-03-19 19:46:02
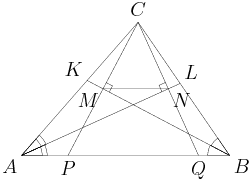

mentalgenius
2011-03-19 19:46:24
congruent
congruent
MathTwo
2011-03-19 19:46:24
angle bisectors/ right angles=> isosceles triangles
angle bisectors/ right angles=> isosceles triangles
aerrowfinn72
2011-03-19 19:46:24
2 isosceles triangles
2 isosceles triangles
rrusczyk
2011-03-19 19:46:42
As advertised, we have congruent right triangles. For example, triangles CMB and PMB are congruent by ASA. What notable bit of information does this give us?
As advertised, we have congruent right triangles. For example, triangles CMB and PMB are congruent by ASA. What notable bit of information does this give us?
aerrowfinn72
2011-03-19 19:47:26
AC = AQ and BC = BP
AC = AQ and BC = BP
BOGTRO
2011-03-19 19:47:27
PB=BC
PB=BC
gh625
2011-03-19 19:47:27
CB=PB
CB=PB
tan90
2011-03-19 19:47:27
PB = CB
PB = CB
rrusczyk
2011-03-19 19:47:48
Please use capital letters when referring to points. I don't read the posts with lowercase point labels.
Please use capital letters when referring to points. I don't read the posts with lowercase point labels.
rrusczyk
2011-03-19 19:47:51
This tells us that BP = CB = 120. So?
This tells us that BP = CB = 120. So?
alligator112
2011-03-19 19:48:08
AP = 5
AP = 5
Jasmine8925
2011-03-19 19:48:08
we can find AP
we can find AP
centralbs
2011-03-19 19:48:08
AP = 5
AP = 5
rrusczyk
2011-03-19 19:48:15
So, AP = AB - BP = 5.
So, AP = AB - BP = 5.
calvinhobbesliker
2011-03-19 19:48:19
Find AQ similarly, then PQ can be found
Find AQ similarly, then PQ can be found
mathepic
2011-03-19 19:48:32
We do the same thing to find BQ, then subtract both
We do the same thing to find BQ, then subtract both
rrusczyk
2011-03-19 19:48:38
What do we get for PQ?
What do we get for PQ?
theone142857
2011-03-19 19:49:06
PQ=112
PQ=112
IsTvOn
2011-03-19 19:49:06
112
112
Alex Song
2011-03-19 19:49:06
112
112
calvinhobbesliker
2011-03-19 19:49:06
112
112
tan90
2011-03-19 19:49:06
112
112
.cpp
2011-03-19 19:49:06
PQ = AB-AP-BQ = 112.
PQ = AB-AP-BQ = 112.
centralbs
2011-03-19 19:49:06
112
112
Kinata12
2011-03-19 19:49:06
112
112
rrusczyk
2011-03-19 19:49:20
Similar to how we found AP, we have AQ = AC = 117, so BQ = AB - AQ = 8.
Similar to how we found AP, we have AQ = AC = 117, so BQ = AB - AQ = 8.
rrusczyk
2011-03-19 19:49:36
So, PQ = AB - AP - BQ = 112.
So, PQ = AB - AP - BQ = 112.
rrusczyk
2011-03-19 19:49:38
Now what?
Now what?
ParallelProcess
2011-03-19 19:50:15
M is the midpoint of CP, and similarly for the opposite side, so MN = 1/2*PQ
M is the midpoint of CP, and similarly for the opposite side, so MN = 1/2*PQ
theone142857
2011-03-19 19:50:15
MN=1/2PQ
MN=1/2PQ
v_Enhance
2011-03-19 19:50:15
MN = 1/2 PQ
MN = 1/2 PQ
calvinhobbesliker
2011-03-19 19:50:15
MN=PQ/2 by similar triangles
MN=PQ/2 by similar triangles
Kinata12
2011-03-19 19:50:15
Use CMN and CPQ similar triangles!
Use CMN and CPQ similar triangles!
Alex Song
2011-03-19 19:50:15
MN is a midline of triangle CPQ; MN = PQ/2
MN is a midline of triangle CPQ; MN = PQ/2
ahaanomegas
2011-03-19 19:50:15
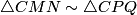
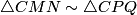
rrusczyk
2011-03-19 19:50:33
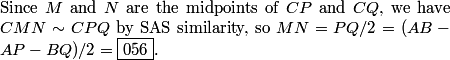
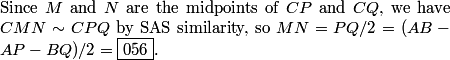
GoldenFrog1618
2011-03-19 19:50:40
I solved this problem initially with the "measure the line" method
I solved this problem initially with the "measure the line" method
rrusczyk
2011-03-19 19:51:01
Funny. Don't underestimate that : I got into MOP my sophomore year largely because of it :)
Funny. Don't underestimate that : I got into MOP my sophomore year largely because of it :)
ahaanomegas
2011-03-19 19:51:11
What is the "measure the line" method?
What is the "measure the line" method?
tiger21
2011-03-19 19:51:25
you use a ruler
you use a ruler
calvinhobbesliker
2011-03-19 19:51:25
Draw the triangle precisely and measure
Draw the triangle precisely and measure
rrusczyk
2011-03-19 19:51:26
Draw to scale. Measure with ruler.
Draw to scale. Measure with ruler.
centralbs
2011-03-19 19:51:28
How do you know its the midline?
How do you know its the midline?
rrusczyk
2011-03-19 19:51:51
Because CM = MP (triangles CMB and CMP are congruent) and CN = NQ.
Because CM = MP (triangles CMB and CMP are congruent) and CN = NQ.
ahaanomegas
2011-03-19 19:51:54
Congruence
Congruence
pi091997
2011-03-19 19:51:54
congruent triangles
congruent triangles
GoldenFrog1618
2011-03-19 19:51:57
M and N are midpoints
M and N are midpoints
ParallelProcess
2011-03-19 19:51:59
on the AIME, if something "looks" parallel like in this diagram, is it usually actually parallel?
on the AIME, if something "looks" parallel like in this diagram, is it usually actually parallel?
rrusczyk
2011-03-19 19:52:11
Dangerous -- it tells you that you should try to prove that it is parallel.
Dangerous -- it tells you that you should try to prove that it is parallel.
rrusczyk
2011-03-19 19:52:32


rrusczyk
2011-03-19 19:52:38
Where do we start?
Where do we start?
professordad
2011-03-19 19:52:51
take every number mod 3
take every number mod 3
bulutcocuk
2011-03-19 19:52:51
mod 3
mod 3
zero.destroyer
2011-03-19 19:52:51
use mods
use mods
policecap
2011-03-19 19:52:51
mod 3
mod 3
superpi83
2011-03-19 19:52:51
reduce in mod 3
reduce in mod 3
theone142857
2011-03-19 19:52:51
mod 3
mod 3
hrithikguy
2011-03-19 19:52:51
rename the digits as 1,2,0,1,2,0,1,2,0
rename the digits as 1,2,0,1,2,0,1,2,0
carmelninja
2011-03-19 19:52:54
look at it in terms of modulo 3
look at it in terms of modulo 3
rrusczyk
2011-03-19 19:52:57
We start by thinking about the numbers mod 3 (that is, their remainders when divided by 3). When determining if the sums of the numbers are multiples of 3, their remainders when divided by 3 are all that matters.
We start by thinking about the numbers mod 3 (that is, their remainders when divided by 3). When determining if the sums of the numbers are multiples of 3, their remainders when divided by 3 are all that matters.
rrusczyk
2011-03-19 19:53:01
So, now we have 3 0's, 3 1's, and 3 2's to place around the nonagons. Suppose we start with a 0. Then, what are our options for the next number going clockwise?
So, now we have 3 0's, 3 1's, and 3 2's to place around the nonagons. Suppose we start with a 0. Then, what are our options for the next number going clockwise?
hrithikguy
2011-03-19 19:53:16
1 or 2
1 or 2
tekgeek
2011-03-19 19:53:16
1 or 2
1 or 2
pi.guy3.14
2011-03-19 19:53:16
1,2 or 2,1
1,2 or 2,1
professordad
2011-03-19 19:53:16
we can have 1 or 2
we can have 1 or 2
EggyLv.999
2011-03-19 19:53:16
2 or 1
2 or 1
zero.destroyer
2011-03-19 19:53:16
1, or 2
1, or 2
Spring
2011-03-19 19:53:16
1 or 2
1 or 2
pi091997
2011-03-19 19:53:16
1 or 2
1 or 2
superpi83
2011-03-19 19:53:16
1 or 2
1 or 2
hrithikguy
2011-03-19 19:53:16
1 or 2 (NOT zero)!
1 or 2 (NOT zero)!
daddy1cherry
2011-03-19 19:53:16
1 or 2
1 or 2
zazz4
2011-03-19 19:53:16
2 or 1
2 or 1
rrusczyk
2011-03-19 19:53:19
We can't have a 0 next. If we place a 0 next, then the following number must also be a 0 to make the sum of the three numbers divisible by 3. But so must the next number, and then next number, and so on.
We can't have a 0 next. If we place a 0 next, then the following number must also be a 0 to make the sum of the three numbers divisible by 3. But so must the next number, and then next number, and so on.
rrusczyk
2011-03-19 19:53:22
What if we place a 1 next?
What if we place a 1 next?
KeepingItReal
2011-03-19 19:53:34
2 must be next
2 must be next
jellymoop
2011-03-19 19:53:34
2
2
arigao2007
2011-03-19 19:53:34
then 2 next
then 2 next
EggyLv.999
2011-03-19 19:53:34
2 next
2 next
pi091997
2011-03-19 19:53:34
then 2
then 2
mthcz11
2011-03-19 19:53:34
wowzo
wowzo
Kinata12
2011-03-19 19:53:34
The next is 2
The next is 2
centralbs
2011-03-19 19:53:34
it has to be a 2
it has to be a 2
professordad
2011-03-19 19:53:34
then the next number is 2
then the next number is 2
superpi83
2011-03-19 19:53:34
then it goes 012012012
then it goes 012012012
theone142857
2011-03-19 19:53:34
2 next
2 next
.cpp
2011-03-19 19:53:34
Then a 2 goes next.
Then a 2 goes next.
alligator112
2011-03-19 19:53:34
then a 2 next!
then a 2 next!
jeff10
2011-03-19 19:53:34
0 1 2 0 1 2 0 1 2
0 1 2 0 1 2 0 1 2
zero.destroyer
2011-03-19 19:53:34
it's 2
it's 2
fortenforge
2011-03-19 19:53:34
Then the number after that is a 2
Then the number after that is a 2
AlphaMath1
2011-03-19 19:53:34
next has to be 2
next has to be 2
alanzee
2011-03-19 19:53:34
next 2, then 0, then 1, 2, ...
next 2, then 0, then 1, 2, ...
rrusczyk
2011-03-19 19:53:38
If we start 0, 1, then the next number must be 2 to make the sum a multiple of 3. Then we have 0, 1, 2.
If we start 0, 1, then the next number must be 2 to make the sum a multiple of 3. Then we have 0, 1, 2.
rrusczyk
2011-03-19 19:53:41
So, the next number must be a 0, and the next a 1, the next a 2, and so on, so we have the pattern
0, 1, 2, 0, 1, 2, 0, 1, 2.
So, the next number must be a 0, and the next a 1, the next a 2, and so on, so we have the pattern
0, 1, 2, 0, 1, 2, 0, 1, 2.
rrusczyk
2011-03-19 19:53:45
How many ways can we stick the numbers around the circle in this pattern?
How many ways can we stick the numbers around the circle in this pattern?
rrusczyk
2011-03-19 19:54:06
(I'm talking about the original 9 numbers)
(I'm talking about the original 9 numbers)
.cpp
2011-03-19 19:54:29
72.
72.
KeepingItReal
2011-03-19 19:54:29
72
72
bulutcocuk
2011-03-19 19:54:29
72
72
superpi83
2011-03-19 19:54:29
fix 9 to some position so there are 2!*3!*3!=72 ways
fix 9 to some position so there are 2!*3!*3!=72 ways
mathepic
2011-03-19 19:54:29
3!3!2!
3!3!2!
kangchangood
2011-03-19 19:54:29
3x3x2x2x2?
3x3x2x2x2?
tekgeek
2011-03-19 19:54:29
We can fix the zero to avoid rotation so there are 3!*3!*2=72 ways
We can fix the zero to avoid rotation so there are 3!*3!*2=72 ways
pi.guy3.14
2011-03-19 19:54:32
72
72
jeff10
2011-03-19 19:54:32
72
72
rrusczyk
2011-03-19 19:54:35
In order to not worry about rotations, we just imagine that we place the 3 (which has remainder 0 when divided by 3) first. From there, we have 3*2*1 = 6 ways to place the 1,4, and 7 in the "remainder 1" slots, and 3*2*1 = 6 ways to place the 2,5, and 8 in the "remainder 2" slots. Finally, we have 2 ways to place the 6 and the 9 in the other two "remainder 0" slots. From 6*6*2 = 72 total ways to place the numbers.
In order to not worry about rotations, we just imagine that we place the 3 (which has remainder 0 when divided by 3) first. From there, we have 3*2*1 = 6 ways to place the 1,4, and 7 in the "remainder 1" slots, and 3*2*1 = 6 ways to place the 2,5, and 8 in the "remainder 2" slots. Finally, we have 2 ways to place the 6 and the 9 in the other two "remainder 0" slots. From 6*6*2 = 72 total ways to place the numbers.
rrusczyk
2011-03-19 19:54:43
Are we finished?
Are we finished?
centralbs
2011-03-19 19:55:07
no
no
pi091997
2011-03-19 19:55:07
no
no
delta1
2011-03-19 19:55:07
the other way
the other way
theone142857
2011-03-19 19:55:07
*2
*2
KeepingItReal
2011-03-19 19:55:07
no
no
policecap
2011-03-19 19:55:07
no *2 again because you can flip it
no *2 again because you can flip it
pi.guy3.14
2011-03-19 19:55:07
no, there are 2 patterns, so 2x72=144
no, there are 2 patterns, so 2x72=144
jellymoop
2011-03-19 19:55:07
no, 021021
no, 021021
EggyLv.999
2011-03-19 19:55:07
nope
nope
chessmaster7
2011-03-19 19:55:07
the order can be reversed
the order can be reversed
delta1
2011-03-19 19:55:07
no
no
BOGTRO
2011-03-19 19:55:07
could also be 021
could also be 021
superpi83
2011-03-19 19:55:07
no we still need the 021021021 case
no we still need the 021021021 case
kangchangood
2011-03-19 19:55:07
0,2,1 case
0,2,1 case
tan90
2011-03-19 19:55:07
It could go 0 2 1 0 2 1
It could go 0 2 1 0 2 1
mthcz11
2011-03-19 19:55:07
not yet, still need to multipy by 2 to get 144
not yet, still need to multipy by 2 to get 144
rrusczyk
2011-03-19 19:55:18
No. We have considered starting 0,0 going clockwise and 0,1 going clockwise. We still have to deal with 0,2.
No. We have considered starting 0,0 going clockwise and 0,1 going clockwise. We still have to deal with 0,2.
j_f_c_w
2011-03-19 19:55:23
No there are 72 ways of arranging the numbers but 2 patters
No there are 72 ways of arranging the numbers but 2 patters
mathepic
2011-03-19 19:55:26
no, double it
no, double it
filetmignon821
2011-03-19 19:55:28
we have to multiply by 2
we have to multiply by 2
rrusczyk
2011-03-19 19:55:31
We get the same thing as 0,1, but the pattern now going clockwise is
0,2,1,0,2,1,0,2,1
We get the same thing as 0,1, but the pattern now going clockwise is
0,2,1,0,2,1,0,2,1
rrusczyk
2011-03-19 19:55:36
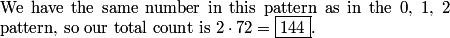
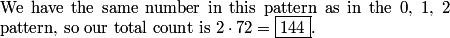
rrusczyk
2011-03-19 19:55:45
Way easier than the previous two!
Way easier than the previous two!
Jasmine8925
2011-03-19 19:55:54
that was a cool problem
that was a cool problem
mthcz11
2011-03-19 19:55:54
yay!
yay!
icecreamcakepie
2011-03-19 19:55:54
nice
nice
anonymous0
2011-03-19 19:55:54
brilliant!
brilliant!
AlphaMath1
2011-03-19 19:55:54
I agree :)
I agree :)
leekspeak
2011-03-19 19:55:54
YES!
YES!
mthcz11
2011-03-19 19:55:54
yes it was :)
yes it was :)
rrusczyk
2011-03-19 19:55:58
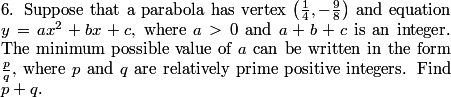
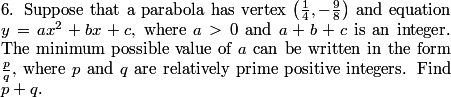
rrusczyk
2011-03-19 19:56:12
Where do we start with this?
Where do we start with this?
leekspeak
2011-03-19 19:56:17
put the quadratic into vertex form
put the quadratic into vertex form
Jasmine8925
2011-03-19 19:56:18
let's write vertex form
let's write vertex form
theone142857
2011-03-19 19:56:20
vertex
vertex
tekgeek
2011-03-19 19:56:29
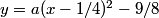
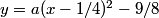
carmelninja
2011-03-19 19:56:29
express quadratic in vertex form
express quadratic in vertex form
Jasmine8925
2011-03-19 19:56:30
y = a(x-1/4)^2 - 9/8
y = a(x-1/4)^2 - 9/8
rrusczyk
2011-03-19 19:56:34
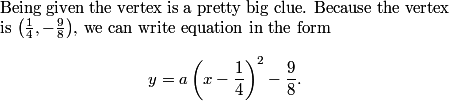
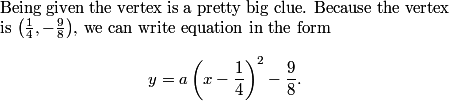
rrusczyk
2011-03-19 19:56:39
We could bash this out and compare it to y = ax^2 + bx + c, but is there a more clever way to proceed?
We could bash this out and compare it to y = ax^2 + bx + c, but is there a more clever way to proceed?
Z91
2011-03-19 19:56:56
a+b+c=f(1)
a+b+c=f(1)
centralbs
2011-03-19 19:56:56
"Keep your eye on the ball" - we want a + b + c, which is the same as p(1)
"Keep your eye on the ball" - we want a + b + c, which is the same as p(1)
hrithikguy
2011-03-19 19:56:56
f(1) = a+b+c
f(1) = a+b+c
zero.destroyer
2011-03-19 19:56:56
f(1)=a+b+c
f(1)=a+b+c
rrusczyk
2011-03-19 19:57:03
The one key piece of information we haven't used yet is that a+b+c is an integer.
The one key piece of information we haven't used yet is that a+b+c is an integer.
delta1
2011-03-19 19:57:09
a+b+c is when x=1
a+b+c is when x=1
rrusczyk
2011-03-19 19:57:18
To use that, we simply let x = 1 in y =ax^2 + bx + c! Doing so gives us y = a + b + c. So, y is an integer when x = 1. How does this help?
To use that, we simply let x = 1 in y =ax^2 + bx + c! Doing so gives us y = a + b + c. So, y is an integer when x = 1. How does this help?
BOGTRO
2011-03-19 19:57:56
9/16a-9/8 is integral
9/16a-9/8 is integral
KeepingItReal
2011-03-19 19:57:57
Plug 1 into vertex form.
Plug 1 into vertex form.
Jasmine8925
2011-03-19 19:57:57
now plug 1 into the vertex form
now plug 1 into the vertex form
hrithikguy
2011-03-19 19:57:57
plug this in the vertext form
plug this in the vertext form
Kinata12
2011-03-19 19:57:57
Plug x=1 into vertex form
Plug x=1 into vertex form
kangchangood
2011-03-19 19:57:57
a(3/4)^2 - 9/8 is integer.
a(3/4)^2 - 9/8 is integer.
alanzee
2011-03-19 19:57:57
a*(3/4)^2-9/8 is an integer
a*(3/4)^2-9/8 is an integer
.cpp
2011-03-19 19:57:57
Thus a(9/16) - 9/8 is an integer.
Thus a(9/16) - 9/8 is an integer.
Jasmine8925
2011-03-19 19:57:57
a(3/4)^2-9/8
a(3/4)^2-9/8
rrusczyk
2011-03-19 19:58:05
We stick x = 1 into our earlier equation with the vertex:
We stick x = 1 into our earlier equation with the vertex:
rrusczyk
2011-03-19 19:58:09
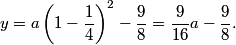
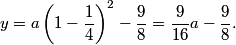
rrusczyk
2011-03-19 19:58:19
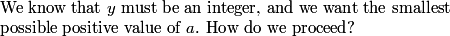
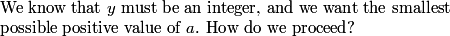
calvinhobbesliker
2011-03-19 19:59:04
set it equal to -1
set it equal to -1
Spring
2011-03-19 19:59:04
y has to be at least -1 for a to be positive
y has to be at least -1 for a to be positive
etude
2011-03-19 19:59:04
a is positive, so y > -9/8 (parabola opens upwards). Thus y = -1.
a is positive, so y > -9/8 (parabola opens upwards). Thus y = -1.
prezcoin
2011-03-19 19:59:04
we get a= (16y-18)/9 is positive, so y= -1 to minimize a
we get a= (16y-18)/9 is positive, so y= -1 to minimize a
rrusczyk
2011-03-19 19:59:15
And what do we get?
And what do we get?
alanzee
2011-03-19 19:59:27
take the fractional part of 9/8, so (9a-2)/16 is an integer => a=2/9
take the fractional part of 9/8, so (9a-2)/16 is an integer => a=2/9
professordad
2011-03-19 19:59:27
9a-18 must be divisible by 16, so 9a = 2 mod 16, a = 2/9 minimum
9a-18 must be divisible by 16, so 9a = 2 mod 16, a = 2/9 minimum
theone142857
2011-03-19 19:59:27
2/9
2/9
centralbs
2011-03-19 19:59:27
2/9 so 11
2/9 so 11
mthcz11
2011-03-19 19:59:27
2/9! :)
2/9! :)
hrithikguy
2011-03-19 19:59:27
a =2/9
a =2/9
skyhog
2011-03-19 19:59:27
a=2/9
a=2/9
BOGTRO
2011-03-19 19:59:27
a=2/9
a=2/9
carmelninja
2011-03-19 19:59:27
a = 2/9
a = 2/9
vcez
2011-03-19 19:59:27
2/9
2/9
rrusczyk
2011-03-19 19:59:32
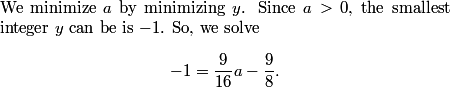
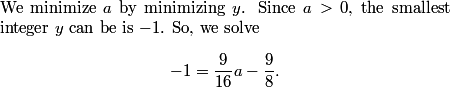
theone142857
2011-03-19 19:59:35
so 011
so 011
vcez
2011-03-19 19:59:35
thus our answers is 2+9=11
thus our answers is 2+9=11
ahaanomegas
2011-03-19 19:59:37
2 + 9 = 011 = Answer
2 + 9 = 011 = Answer
rrusczyk
2011-03-19 19:59:42
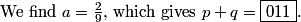
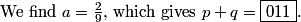
rrusczyk
2011-03-19 19:59:56
As an extra challenge, see if you can find a geometric inspiration for this solution.
As an extra challenge, see if you can find a geometric inspiration for this solution.
rrusczyk
2011-03-19 20:00:08
(On your own. We have 9 more problems to do!
(On your own. We have 9 more problems to do!
rrusczyk
2011-03-19 20:00:18
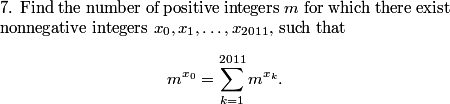
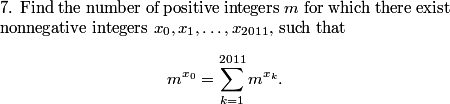
rrusczyk
2011-03-19 20:00:26
This is a pretty confusing problem at first glance. What's one way we can play with the problem a bit to get used to it?
This is a pretty confusing problem at first glance. What's one way we can play with the problem a bit to get used to it?
leekspeak
2011-03-19 20:00:36
Blindly guess, then run home and make a sacrifice to Jupiter
Blindly guess, then run home and make a sacrifice to Jupiter
rrusczyk
2011-03-19 20:00:40
That might work.
That might work.
policecap
2011-03-19 20:00:49
try out small m
try out small m
.cpp
2011-03-19 20:00:49
Try small values!
Try small values!
Spring
2011-03-19 20:00:49
Try some small integers for m
Try some small integers for m
Kinata12
2011-03-19 20:00:53
Try various values of m
Try various values of m
rrusczyk
2011-03-19 20:00:58
We can pick a specific m and mess around with it. We'll pick a small m, since big numbers are scary. Where should we start?
We can pick a specific m and mess around with it. We'll pick a small m, since big numbers are scary. Where should we start?
EggyLv.999
2011-03-19 20:01:07
2
2
carmelninja
2011-03-19 20:01:07
m=2
m=2
hrithikguy
2011-03-19 20:01:07
2
2
calvinhobbesliker
2011-03-19 20:01:07
2
2
hrithikguy
2011-03-19 20:01:07
m = 2
m = 2
delta1
2011-03-19 20:01:07
2
2
rrusczyk
2011-03-19 20:01:14
m=1 can't possibly work. So, we'll start with m =2.
m=1 can't possibly work. So, we'll start with m =2.
rrusczyk
2011-03-19 20:01:21
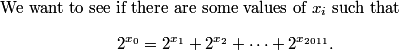
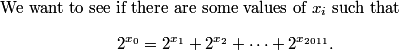
rrusczyk
2011-03-19 20:01:28
What might we wonder first about the terms on the right?
What might we wonder first about the terms on the right?
Spring
2011-03-19 20:02:29
how many 2^0=1 terms
how many 2^0=1 terms
rrusczyk
2011-03-19 20:02:47
We might wonder if we can have any of the x_i on the right be 0's. That is, can any of the terms on the right be simply 1?
We might wonder if we can have any of the x_i on the right be 0's. That is, can any of the terms on the right be simply 1?
rrusczyk
2011-03-19 20:02:50
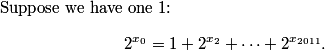
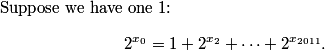
delta1
2011-03-19 20:03:10
two 1s
two 1s
skyhog
2011-03-19 20:03:10
No. There have to be an even number of 1's
No. There have to be an even number of 1's
AlphaMath1
2011-03-19 20:03:17
we must have another 1 because 2^{x_0} is even
we must have another 1 because 2^{x_0} is even
rrusczyk
2011-03-19 20:03:19
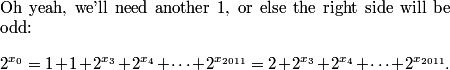
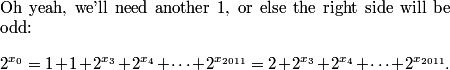
rrusczyk
2011-03-19 20:03:23
Now what do we need?
Now what do we need?
theone142857
2011-03-19 20:03:44
2
2
delta1
2011-03-19 20:03:44
a 2
a 2
.cpp
2011-03-19 20:03:44
2^1 seems like a good idea.
2^1 seems like a good idea.
bojobo
2011-03-19 20:03:48
and repeat
and repeat
carmelninja
2011-03-19 20:03:48
we need one 2^1 so the LHS will be divisible by 4
we need one 2^1 so the LHS will be divisible by 4
EggyLv.999
2011-03-19 20:03:48
some 2^1
some 2^1
rrusczyk
2011-03-19 20:03:51
Now we need another 2. This could from two more 1's or from a 2^1 term, but we definitely need another 2 somewhere. Otherwise, the right-hand side will not be divisible by 4.
Now we need another 2. This could from two more 1's or from a 2^1 term, but we definitely need another 2 somewhere. Otherwise, the right-hand side will not be divisible by 4.
rrusczyk
2011-03-19 20:03:56
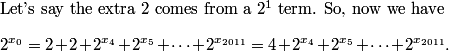
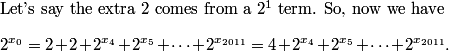
rrusczyk
2011-03-19 20:04:00
Now what do we need?
Now what do we need?
delta1
2011-03-19 20:04:12
and a 4
and a 4
pi.guy3.14
2011-03-19 20:04:12
4
4
hrithikguy
2011-03-19 20:04:12
a 4
a 4
EggyLv.999
2011-03-19 20:04:12
4
4
SuperNerd123
2011-03-19 20:04:12
4
4
skyhog
2011-03-19 20:04:12
Another 4
Another 4
policecap
2011-03-19 20:04:12
4, 8 and so on
4, 8 and so on
dlennon
2011-03-19 20:04:12
A 4.
A 4.
delta1
2011-03-19 20:04:12
and so on
and so on
rrusczyk
2011-03-19 20:04:16
Now, if we don't have another 4 from somewhere, the right side can't be a multiple of 8. We can get a 4 in a lot of ways (1+1+2), (2+2), etc., but it's easiest if we just have a 2^2 term.
Now, if we don't have another 4 from somewhere, the right side can't be a multiple of 8. We can get a 4 in a lot of ways (1+1+2), (2+2), etc., but it's easiest if we just have a 2^2 term.
rrusczyk
2011-03-19 20:04:23
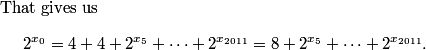
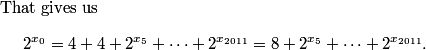
icecreamcakepie
2011-03-19 20:05:25
then a 16,32,64,128, and so on
then a 16,32,64,128, and so on
rrusczyk
2011-03-19 20:05:37
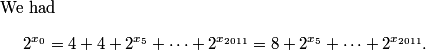
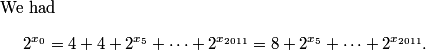
PiquantPeppers
2011-03-19 20:05:37
we repeat this process
we repeat this process
rrusczyk
2011-03-19 20:05:41
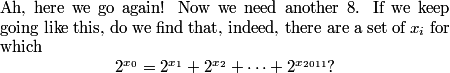
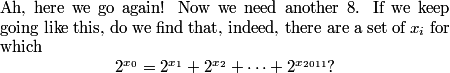
hrithikguy
2011-03-19 20:06:08
Boy SOPRANO!! Can you start a chat with me? I am TOTALLY lost!!
Boy SOPRANO!! Can you start a chat with me? I am TOTALLY lost!!
centralbs
2011-03-19 20:06:08
We can figure that out from the geometric sequence formula, you get 2^{n+1} -1, and then we added the extra 1
We can figure that out from the geometric sequence formula, you get 2^{n+1} -1, and then we added the extra 1
delta1
2011-03-19 20:06:08
yes
yes
numberwiz
2011-03-19 20:06:08
yes!
yes!
.cpp
2011-03-19 20:06:08
Yes, absolutely!
Yes, absolutely!
superpi83
2011-03-19 20:06:08
yes.
yes.
JSGandora
2011-03-19 20:06:08
yes, yes there are
yes, yes there are
Kinata12
2011-03-19 20:06:08
Yes, both sides are 2^2010
Yes, both sides are 2^2010
professordad
2011-03-19 20:06:10
yes, there is a set
yes, there is a set
rrusczyk
2011-03-19 20:06:13
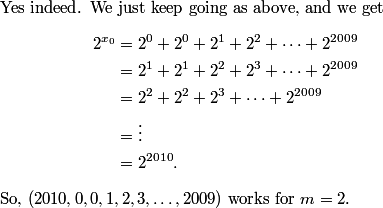
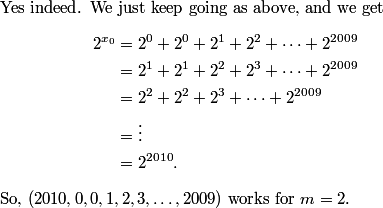
rrusczyk
2011-03-19 20:06:36
Now, this may not be the only way to make it work for 2. We were just trying to see if we could find a way to make it work for 2.
Now, this may not be the only way to make it work for 2. We were just trying to see if we could find a way to make it work for 2.
theone142857
2011-03-19 20:06:38
m=3!!!!!!!!!!!!!!!!!!
m=3!!!!!!!!!!!!!!!!!!
rrusczyk
2011-03-19 20:06:41
Maybe 2 is special. Let's see if we can do the same thing with 3.
Maybe 2 is special. Let's see if we can do the same thing with 3.
rrusczyk
2011-03-19 20:06:48
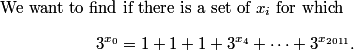
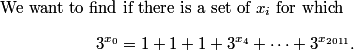
rrusczyk
2011-03-19 20:06:54
We'll start out with some 1's, since that worked so well when m=2. How many do we need?
We'll start out with some 1's, since that worked so well when m=2. How many do we need?
centrino
2011-03-19 20:07:20
3
3
theone142857
2011-03-19 20:07:20
3
3
Jasmine8925
2011-03-19 20:07:20
3 1s
3 1s
JSGandora
2011-03-19 20:07:20
we need three ones
we need three ones
Kinata12
2011-03-19 20:07:23
3
3
skyhog
2011-03-19 20:07:23
3 of them (they're already there...)
3 of them (they're already there...)
superpi83
2011-03-19 20:07:23
3
3
rrusczyk
2011-03-19 20:07:27
If we have any 1's, we need 3, otherwise we won't have a multiple of 3 on the right-hand side. (We could have more, but we'll start with three 1's, just like we started with two 1's for m=2.)
If we have any 1's, we need 3, otherwise we won't have a multiple of 3 on the right-hand side. (We could have more, but we'll start with three 1's, just like we started with two 1's for m=2.)
rrusczyk
2011-03-19 20:07:30
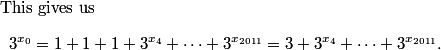
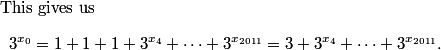
rrusczyk
2011-03-19 20:07:42
This looks familiar.
This looks familiar.
rrusczyk
2011-03-19 20:07:47
What are we going to need on the right-hand side?
What are we going to need on the right-hand side?
pi.guy3.14
2011-03-19 20:07:59
wups, we need 2 3's
wups, we need 2 3's
Jasmine8925
2011-03-19 20:07:59
two 3s
two 3s
dlennon
2011-03-19 20:07:59
We then need 2 more 3s
We then need 2 more 3s
tan90
2011-03-19 20:07:59
Two more 3's
Two more 3's
rrusczyk
2011-03-19 20:08:03
We're going to need some more 3's to go with our first 3, otherwise the right side won't be a multiple of 9. Specifically, we'll need a pair of them. As with our m=2 case, there are a lot of ways to get our needed extra terms. We're lazy, so we'll take the easiest way, by including a couple 3^1 terms on the right side.
We're going to need some more 3's to go with our first 3, otherwise the right side won't be a multiple of 9. Specifically, we'll need a pair of them. As with our m=2 case, there are a lot of ways to get our needed extra terms. We're lazy, so we'll take the easiest way, by including a couple 3^1 terms on the right side.
rrusczyk
2011-03-19 20:08:06
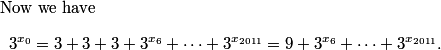
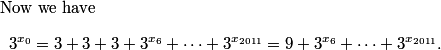
.cpp
2011-03-19 20:08:27
Two more 3 terms, then two more 9 terms, ...
Two more 3 terms, then two more 9 terms, ...
policecap
2011-03-19 20:08:27
2 9's, and so on
2 9's, and so on
delta1
2011-03-19 20:08:27
two 9's
two 9's
Kinata12
2011-03-19 20:08:27
Just add 2 at a time of powers of 3
Just add 2 at a time of powers of 3
dlennon
2011-03-19 20:08:27
And 2 more 9s
And 2 more 9s
tiger21
2011-03-19 20:08:27
and then 2 9's
and then 2 9's
jeff10
2011-03-19 20:08:27
2 more 3s
2 more 3s
KeepingItReal
2011-03-19 20:08:27
Now we need 2 9's.
Now we need 2 9's.
rrusczyk
2011-03-19 20:08:30
And now we need a couple more 3^2 terms, and then we'll need a couple more 3^3 terms, and so on.
And now we need a couple more 3^2 terms, and then we'll need a couple more 3^3 terms, and so on.
rrusczyk
2011-03-19 20:08:34
Will this work? Does it generate a set of x_i that satisfy the original equation when m = 3?
Will this work? Does it generate a set of x_i that satisfy the original equation when m = 3?
delta1
2011-03-19 20:08:53
yes
yes
swimfreak07059
2011-03-19 20:08:54
yes
yes
.cpp
2011-03-19 20:08:54
Yes.
Yes.
EggyLv.999
2011-03-19 20:08:54
yes
yes
Kinata12
2011-03-19 20:08:54
Yes, 2011=3+2+2+2...
Yes, 2011=3+2+2+2...
dlennon
2011-03-19 20:08:55
Yes it works.
Yes it works.
Zadig
2011-03-19 20:08:58
2011 = 3 + 2(1004) yes
2011 = 3 + 2(1004) yes
rrusczyk
2011-03-19 20:09:02
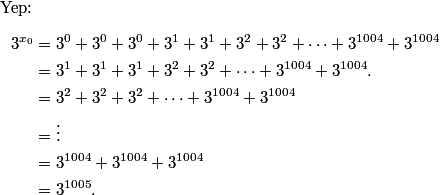
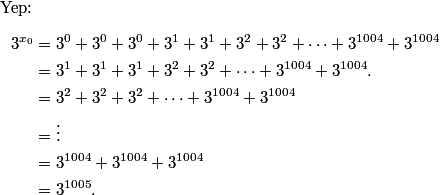
rrusczyk
2011-03-19 20:09:07
We have another winner.
We have another winner.
rrusczyk
2011-03-19 20:09:12
We should stop now and think about why this process is finding sets of x_i that work for a given m. Then, maybe we can figure out which m will work. (Of course, this process may not give us the only set of x_i that work, but, first things first -- let's at least see if we can figure out the m that work with this process.)
We should stop now and think about why this process is finding sets of x_i that work for a given m. Then, maybe we can figure out which m will work. (Of course, this process may not give us the only set of x_i that work, but, first things first -- let's at least see if we can figure out the m that work with this process.)
rrusczyk
2011-03-19 20:09:16
What exactly is our process here for a given value of m?
What exactly is our process here for a given value of m?
rrusczyk
2011-03-19 20:09:20
A) We start with m terms of the form m^0. These are our 1's, and they add up to m.
A) We start with m terms of the form m^0. These are our 1's, and they add up to m.
rrusczyk
2011-03-19 20:09:35
B) Then, we need m-1 terms of the form m^1 to combine with this initial m to give us an m^2.
B) Then, we need m-1 terms of the form m^1 to combine with this initial m to give us an m^2.
rrusczyk
2011-03-19 20:09:39
C) Then, we need m-1 terms of the form m^2 to combine with this initial m^2 to give us an m^3.
C) Then, we need m-1 terms of the form m^2 to combine with this initial m^2 to give us an m^3.
rrusczyk
2011-03-19 20:09:56
D) And so on.
D) And so on.
rrusczyk
2011-03-19 20:10:01
We want this process to produce 2011 terms total, and it did for m=2 and m=3. Will it always produce 2011 terms?
We want this process to produce 2011 terms total, and it did for m=2 and m=3. Will it always produce 2011 terms?
rrusczyk
2011-03-19 20:10:11
(That is, can we always hit 2011 exactly)
(That is, can we always hit 2011 exactly)
delta1
2011-03-19 20:10:18
no
no
Jasmine8925
2011-03-19 20:10:18
no
no
centrino
2011-03-19 20:10:18
no
no
.cpp
2011-03-19 20:10:18
No.
No.
gh625
2011-03-19 20:10:18
no
no
theone142857
2011-03-19 20:10:18
no
no
leekspeak
2011-03-19 20:10:20
no
no
rrusczyk
2011-03-19 20:10:23
No, it won't. Can we write an expression for how many terms it will produce?
No, it won't. Can we write an expression for how many terms it will produce?
numberwiz
2011-03-19 20:10:52
in general, if a can be an int., x + a(x-1) = 2011
in general, if a can be an int., x + a(x-1) = 2011
Kinata12
2011-03-19 20:10:52
m+j(m-1)
m+j(m-1)
policecap
2011-03-19 20:10:52
m+(m-1)*k for some k
m+(m-1)*k for some k
Spring
2011-03-19 20:10:57
m+n(m-1)
m+n(m-1)
carmelninja
2011-03-19 20:10:57
m + n(m-1)
m + n(m-1)
rrusczyk
2011-03-19 20:11:02
Yes. We have m terms initially, and then a bunch of groups of (m-1) terms. So, for some value of k, there are
m+k(m-1)
terms.
Yes. We have m terms initially, and then a bunch of groups of (m-1) terms. So, for some value of k, there are
m+k(m-1)
terms.
rrusczyk
2011-03-19 20:11:10
Therefore, we need there to be some value of k for which
m + k(m-1) = 2011
Therefore, we need there to be some value of k for which
m + k(m-1) = 2011
rrusczyk
2011-03-19 20:11:17
What can we do with this?
What can we do with this?
Jasmine8925
2011-03-19 20:11:47
so 2011 = 1 (mod m-1)
so 2011 = 1 (mod m-1)
leekspeak
2011-03-19 20:11:47
factor!
factor!
.cpp
2011-03-19 20:11:47
(k+1)(m-1) = 2010.
(k+1)(m-1) = 2010.
billybob42
2011-03-19 20:11:47
find all m such that m|2010
find all m such that m|2010
prezcoin
2011-03-19 20:11:47
m= (m-1) +1, so 2010= (k+1)(m-1)
m= (m-1) +1, so 2010= (k+1)(m-1)
pi091997
2011-03-19 20:11:51
(k+1)(m-1)=2010
(k+1)(m-1)=2010
jeff10
2011-03-19 20:11:51
FACTOR!
FACTOR!
rrusczyk
2011-03-19 20:11:54
Subtracting 1 from both sides allows us to factor:
(m-1) + k(m-1) = 2010,
so
(m-1)(k+1) = 2010
Subtracting 1 from both sides allows us to factor:
(m-1) + k(m-1) = 2010,
so
(m-1)(k+1) = 2010
rrusczyk
2011-03-19 20:12:08
And what does this tell us?
And what does this tell us?
bojobo
2011-03-19 20:12:33
all of the factors of 2010 work
all of the factors of 2010 work
ahaanomegas
2011-03-19 20:12:33
m - 1 and k + 1 are both factors of 2010
m - 1 and k + 1 are both factors of 2010
superpi83
2011-03-19 20:12:33
every m corresponds to a factor of 2010
every m corresponds to a factor of 2010
JoeJack
2011-03-19 20:12:33
we're looking for the number of factors of 2010
we're looking for the number of factors of 2010
JSGandora
2011-03-19 20:12:33
This tell us there are as many ms as there are as many factors of 2010
This tell us there are as many ms as there are as many factors of 2010
girishvar12
2011-03-19 20:12:33
they have to be factors of 2010
they have to be factors of 2010
leekspeak
2011-03-19 20:12:39
the possible values of m are the number of factors of 2010
the possible values of m are the number of factors of 2010
.cpp
2011-03-19 20:12:39
m-1 is a factor of 2010, of which there are 16. So m has 16 values here.
m-1 is a factor of 2010, of which there are 16. So m has 16 values here.
pi091997
2011-03-19 20:12:39
m-1 divides 2010
m-1 divides 2010
rrusczyk
2011-03-19 20:12:46
So, if m-1 divides 2010, then our process will give us a set of x_i for that value of m. Therefore, all of the positive divisors (including 1 and 2010) give us solutions.
So, if m-1 divides 2010, then our process will give us a set of x_i for that value of m. Therefore, all of the positive divisors (including 1 and 2010) give us solutions.
Jasmine8925
2011-03-19 20:13:13
2010 = 2*3*5*67
2010 = 2*3*5*67
delta1
2011-03-19 20:13:13
16 possible values of m-1, so 16 possible values of m
16 possible values of m-1, so 16 possible values of m
tan90
2011-03-19 20:13:13
2010 = 2 * 3 * 5 * 67
2010 = 2 * 3 * 5 * 67
policecap
2011-03-19 20:13:13
so theres 2^4=16
so theres 2^4=16
superpi83
2011-03-19 20:13:13
2010=2*3*5*67 so there are 2*2*2*2=16 factors of 2010
2010=2*3*5*67 so there are 2*2*2*2=16 factors of 2010
professordad
2011-03-19 20:13:13
and 2010 has 16 factors
and 2010 has 16 factors
girishvar12
2011-03-19 20:13:13
so 16 numbers work, 016
so 16 numbers work, 016
KeepingItReal
2011-03-19 20:13:13
There are 16 positive divisors
There are 16 positive divisors
policecap
2011-03-19 20:13:13
2*3*5*67=2010, so 2*2*2*2 divisors
2*3*5*67=2010, so 2*2*2*2 divisors
NoWayHaze
2011-03-19 20:13:25
how doesn't 2011^2 = 2011^1 + 2011^1 + 2011^1 ..... 2011^1 work?
how doesn't 2011^2 = 2011^1 + 2011^1 + 2011^1 ..... 2011^1 work?
rrusczyk
2011-03-19 20:13:36
Yep. m=2011 means 2011 - 1 divides 2010.
Yep. m=2011 means 2011 - 1 divides 2010.
.cpp
2011-03-19 20:13:39
We're using m-1, not m
We're using m-1, not m
rrusczyk
2011-03-19 20:13:42
Exactly.
Exactly.
Jasmine8925
2011-03-19 20:13:47
is this the only way to get solutions?
is this the only way to get solutions?
rrusczyk
2011-03-19 20:13:53
Excellent question.
Excellent question.
SuperNerd123
2011-03-19 20:14:07
Wait, don't we have to disclude 1?
Wait, don't we have to disclude 1?
carmelninja
2011-03-19 20:14:36
2-1 = 1
2-1 = 1
skyhog
2011-03-19 20:14:36
m-1=1 which is just the m=2 case we already showed works
m-1=1 which is just the m=2 case we already showed works
superpi83
2011-03-19 20:14:39
1 was never a valid m. 1 was a valid m-1, which corresponded to 2
1 was never a valid m. 1 was a valid m-1, which corresponded to 2
rrusczyk
2011-03-19 20:14:41
No: m=2 when m-1 is 1.
No: m=2 when m-1 is 1.
rrusczyk
2011-03-19 20:14:57
I want to get back to Jasmine's question.
I want to get back to Jasmine's question.
rrusczyk
2011-03-19 20:15:06
We're not finished. There might be some other process that gives us more values of m that work. That said, you'd be forgiven for deciding the work we did so far was about the difficulty level of a #7 on the AIME, assuming the 16 we have found are the only ones that work, and moving on. But let's go ahead and see if we can figure out what's going on here in the whole problem, and prove that these are the only 16 that work.
We're not finished. There might be some other process that gives us more values of m that work. That said, you'd be forgiven for deciding the work we did so far was about the difficulty level of a #7 on the AIME, assuming the 16 we have found are the only ones that work, and moving on. But let's go ahead and see if we can figure out what's going on here in the whole problem, and prove that these are the only 16 that work.
rrusczyk
2011-03-19 20:15:24
rrusczyk
2011-03-19 20:15:30
In our work so far, we discovered that we have a solution when m-1 divides 2010. This m-1 seems important. Can we jam m-1 terms into this equation? If so, how?
In our work so far, we discovered that we have a solution when m-1 divides 2010. This m-1 seems important. Can we jam m-1 terms into this equation? If so, how?
rrusczyk
2011-03-19 20:16:10
I want to start from the original equation and get some m-1 terms in there.
I want to start from the original equation and get some m-1 terms in there.
Jasmine8925
2011-03-19 20:16:38
(m-1)^x_o
(m-1)^x_o
rrusczyk
2011-03-19 20:16:47
We'd like there to be factors of m-1, yes
We'd like there to be factors of m-1, yes
Kinata12
2011-03-19 20:16:49
If you subtract 1 from m^x_k, you can factor out m-1
If you subtract 1 from m^x_k, you can factor out m-1
rrusczyk
2011-03-19 20:16:53
And that will make them!
And that will make them!
rrusczyk
2011-03-19 20:16:58
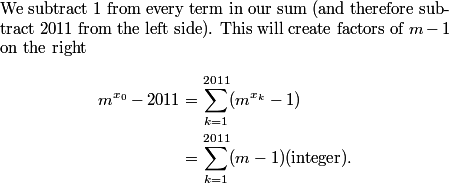
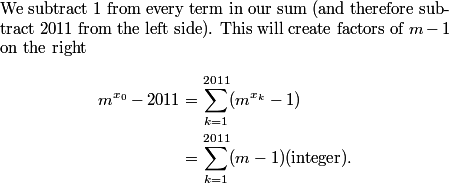
rrusczyk
2011-03-19 20:17:32
And what do we do about the left side?
And what do we do about the left side?
.cpp
2011-03-19 20:18:05
[m^(x_0)-1]-2010.
[m^(x_0)-1]-2010.
delta1
2011-03-19 20:18:05
m^(x_0)-1-2010
m^(x_0)-1-2010
carmelninja
2011-03-19 20:18:05
(m^x_0 - 1) - 2010
(m^x_0 - 1) - 2010
Kinata12
2011-03-19 20:18:05
Subtract 1 from m^x_0 and add it to -2011
Subtract 1 from m^x_0 and add it to -2011
rrusczyk
2011-03-19 20:18:10
We'd like an m-1 over there, and we want a 2010 somewhere, so we break 2011 into 1 + 2010:
We'd like an m-1 over there, and we want a 2010 somewhere, so we break 2011 into 1 + 2010:
rrusczyk
2011-03-19 20:18:14
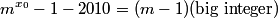
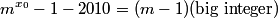
rrusczyk
2011-03-19 20:18:29
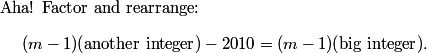
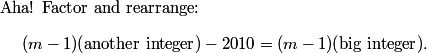
rrusczyk
2011-03-19 20:18:36
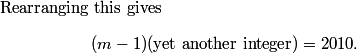
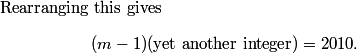
rrusczyk
2011-03-19 20:18:48
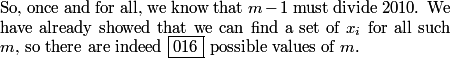
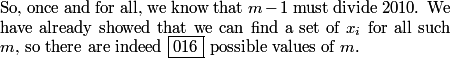
leekspeak
2011-03-19 20:19:03
woah thats brilliant
woah thats brilliant
.cpp
2011-03-19 20:19:03
Thus, (m-1) is a factor of 2010, so our solutions are the only ones.
Thus, (m-1) is a factor of 2010, so our solutions are the only ones.
rrusczyk
2011-03-19 20:19:13
If this were the USAMO, that's what you'd have to do.
If this were the USAMO, that's what you'd have to do.
rrusczyk
2011-03-19 20:19:26
We will do one more problem, and then take a short break
We will do one more problem, and then take a short break
adalander
2011-03-19 20:19:48
Is that a USAMO level problem?
Is that a USAMO level problem?
Jasmine8925
2011-03-19 20:19:48
could that be an easy USAMO problem?
could that be an easy USAMO problem?
rrusczyk
2011-03-19 20:19:54
Maybe early USAJMO
Maybe early USAJMO
rrusczyk
2011-03-19 20:20:00


rrusczyk
2011-03-19 20:20:12
Jasmine8925
2011-03-19 20:20:18
are we given a diagram?
are we given a diagram?
rrusczyk
2011-03-19 20:20:23
Yes, it was on the test.
Yes, it was on the test.
policecap
2011-03-19 20:20:38
the heights from A to UV, B to YZ, and C to WX are all h
the heights from A to UV, B to YZ, and C to WX are all h
Kinata12
2011-03-19 20:20:55
Each small triangle has the same height
Each small triangle has the same height
rrusczyk
2011-03-19 20:20:58
Exactly. That's what we mean by the table coming out to be level.
Exactly. That's what we mean by the table coming out to be level.
rrusczyk
2011-03-19 20:21:10
What's our first observation we can make that will simplify our work for finding the maximal height.
What's our first observation we can make that will simplify our work for finding the maximal height.
Jasmine8925
2011-03-19 20:21:22
what is a "right angle fold"?
what is a "right angle fold"?
rrusczyk
2011-03-19 20:21:46
Folded so that the plane of the fold is perpendicular to the plane of the original table
Folded so that the plane of the fold is perpendicular to the plane of the original table
rrusczyk
2011-03-19 20:22:11
Now, what are we going to do about finding the largest possible height?
Now, what are we going to do about finding the largest possible height?
ParallelProcess
2011-03-19 20:22:14
the max height is when you have a collision of smaller triangles
the max height is when you have a collision of smaller triangles
rrusczyk
2011-03-19 20:22:18
Exactly.
Exactly.
tan90
2011-03-19 20:22:20
Two of the sub-triangles (like AVU) must touch at one point to maximize height.
Two of the sub-triangles (like AVU) must touch at one point to maximize height.
rrusczyk
2011-03-19 20:22:24
If h is maximized then two of the folds must pass through the same point on the perimeter of the triangle. Otherwise, we can increase h a little bit by moving all three folds closer to the center of ABC. This makes life a lot easier. Here's our new diagram:
If h is maximized then two of the folds must pass through the same point on the perimeter of the triangle. Otherwise, we can increase h a little bit by moving all three folds closer to the center of ABC. This makes life a lot easier. Here's our new diagram:
rrusczyk
2011-03-19 20:22:29

Maxima
2011-03-19 20:22:33
What do they mean by maximum possible height?
What do they mean by maximum possible height?
rrusczyk
2011-03-19 20:22:44
We want to be able to fold as far in as possible.
We want to be able to fold as far in as possible.
rrusczyk
2011-03-19 20:23:00
I've just included the two folds that hit at a point. We don't know for sure which two folds it will be that meet at a common point, but we'll go ahead and work out the case above and leave the side lengths as variables (a=BC, b=AC, c=AB). Hopefully our work will reveal which folds intersect.
I've just included the two folds that hit at a point. We don't know for sure which two folds it will be that meet at a common point, but we'll go ahead and work out the case above and leave the side lengths as variables (a=BC, b=AC, c=AB). Hopefully our work will reveal which folds intersect.
skyhog
2011-03-19 20:23:09
How do we know which of the two triangles "collide" ?
How do we know which of the two triangles "collide" ?
rrusczyk
2011-03-19 20:23:19
We don't know for sure; we'll come back to that.
We don't know for sure; we'll come back to that.
rrusczyk
2011-03-19 20:23:46
For now, we'll just work with this in terms of side lengths a,b,c, and then hope our result will tell us which folds collide.
For now, we'll just work with this in terms of side lengths a,b,c, and then hope our result will tell us which folds collide.
rrusczyk
2011-03-19 20:23:49
What should we do with this?
What should we do with this?
rrusczyk
2011-03-19 20:24:02
What should we add to this diagram?
What should we add to this diagram?
skyhog
2011-03-19 20:24:12
altitudes
altitudes
kangchangood
2011-03-19 20:24:12
h things?
h things?
carmelninja
2011-03-19 20:24:12
the altitudes
the altitudes
rrusczyk
2011-03-19 20:24:16
We include the heights from C and B to their respective folds. These heights have length h_A, the desired height of the table.
We include the heights from C and B to their respective folds. These heights have length h_A, the desired height of the table.
rrusczyk
2011-03-19 20:24:19
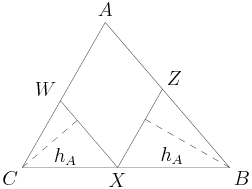

rrusczyk
2011-03-19 20:24:29
Where do we go from here? We'd like to use the fact that these heights are the same; how can we relate these two small triangles to each other?
Where do we go from here? We'd like to use the fact that these heights are the same; how can we relate these two small triangles to each other?
AlphaMath1
2011-03-19 20:24:44
similar triangles
similar triangles
leekspeak
2011-03-19 20:24:44
they are similar
they are similar
billybob42
2011-03-19 20:24:44
similarity
similarity
Cortana
2011-03-19 20:24:44
similar triangles
similar triangles
carmelninja
2011-03-19 20:24:44
similarity
similarity
apple.singer
2011-03-19 20:24:44
similar?
similar?
dlennon
2011-03-19 20:24:44
They are similar
They are similar
hrithikguy
2011-03-19 20:24:44
same area?
same area?
rrusczyk
2011-03-19 20:24:52
There are a lot of ways to go from here. We can note that these two little triangles are similar and go from there. A somewhat slicker solution goes through the larger triangle. How can we relate these little triangles to the larger triangle?
There are a lot of ways to go from here. We can note that these two little triangles are similar and go from there. A somewhat slicker solution goes through the larger triangle. How can we relate these little triangles to the larger triangle?
leekspeak
2011-03-19 20:25:18
similar
similar
centralbs
2011-03-19 20:25:18
similar
similar
Titandrake
2011-03-19 20:25:18
Each little triangle similar to larger triangle. Find heights of large triangle
Each little triangle similar to larger triangle. Find heights of large triangle
KeepingItReal
2011-03-19 20:25:18
similar
similar
jeff10
2011-03-19 20:25:18
They are both similar to the large triangle.
They are both similar to the large triangle.
apple.singer
2011-03-19 20:25:18
similar again?
similar again?
rrusczyk
2011-03-19 20:25:23
Each little triangle is similar to the larger triangle. So, what does that tell us about CX?
Each little triangle is similar to the larger triangle. So, what does that tell us about CX?
.cpp
2011-03-19 20:26:17
CX/CB = h_a/h_(C to AB).
CX/CB = h_a/h_(C to AB).
rrusczyk
2011-03-19 20:26:24
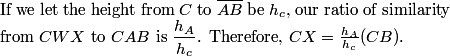
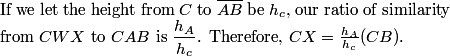
rrusczyk
2011-03-19 20:26:44
And XB?
And XB?
.cpp
2011-03-19 20:27:25
XB/BC = h_A/h_b.
XB/BC = h_A/h_b.
KeepingItReal
2011-03-19 20:27:25
XB/BC = h_A/ h _ (B to CA)
XB/BC = h_A/ h _ (B to CA)
rrusczyk
2011-03-19 20:27:30
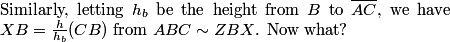
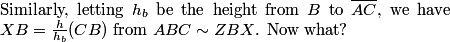
policecap
2011-03-19 20:28:12
add
add
.cpp
2011-03-19 20:28:12
CX+XB = CB.
CX+XB = CB.
fortenforge
2011-03-19 20:28:12
Add the two equations
Add the two equations
rrusczyk
2011-03-19 20:28:16
We simply add CX and XB. We have CX + XB = BC, so
We simply add CX and XB. We have CX + XB = BC, so
rrusczyk
2011-03-19 20:28:21
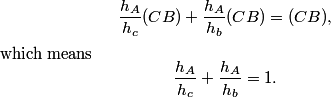
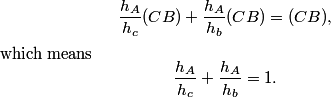
rrusczyk
2011-03-19 20:28:25
And how will we deal with h_b and h_c?
And how will we deal with h_b and h_c?
Cortana
2011-03-19 20:28:53
find the area
find the area
etude
2011-03-19 20:28:53
We find them using our area formulae.
We find them using our area formulae.
s.homberg
2011-03-19 20:28:53
find them with Heron's and 1/2 bh
find them with Heron's and 1/2 bh
AlphaMath1
2011-03-19 20:28:57
we can calculate that using herons then multiply by 2 then divide by the base
we can calculate that using herons then multiply by 2 then divide by the base
rrusczyk
2011-03-19 20:29:18
Do we actually have to find h_b and h_c?
Do we actually have to find h_b and h_c?
iamthygod!!!!!!
2011-03-19 20:29:31
no
no
ChipDale
2011-03-19 20:29:31
no
no
danielguo94
2011-03-19 20:29:31
no
no
rrusczyk
2011-03-19 20:29:34
Why not?
Why not?
rrusczyk
2011-03-19 20:29:45
How can we just skip around that?
How can we just skip around that?
policecap
2011-03-19 20:30:00
area/side = height, use that for all h's
area/side = height, use that for all h's
rrusczyk
2011-03-19 20:30:14
Exactly. Let K be the area, and what do we get for h_A?
Exactly. Let K be the area, and what do we get for h_A?
.cpp
2011-03-19 20:31:19
2K/(b+c).
2K/(b+c).
rrusczyk
2011-03-19 20:31:25
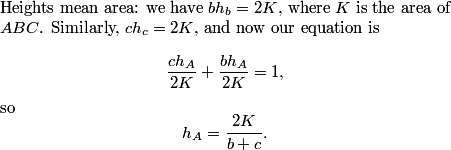
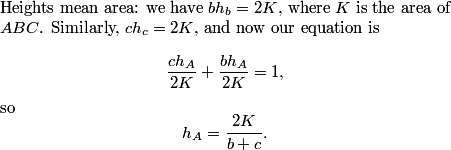
rrusczyk
2011-03-19 20:31:39
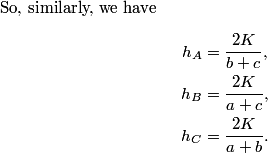
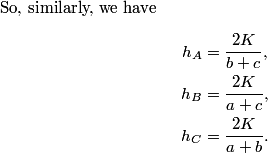
rrusczyk
2011-03-19 20:32:22
These are the three heights we get if we have folds meet on each pair of sides. h_A is what we get when the folds meet opposite A, h_B is what we get when the folds meet opposite B, etc.
These are the three heights we get if we have folds meet on each pair of sides. h_A is what we get when the folds meet opposite A, h_B is what we get when the folds meet opposite B, etc.
rrusczyk
2011-03-19 20:32:26
Now, which one is the winner?
Now, which one is the winner?
rrusczyk
2011-03-19 20:32:35
Do we want the largest or the smallest?
Do we want the largest or the smallest?
GoldenFrog1618
2011-03-19 20:32:52
pick the minimal h_A
pick the minimal h_A
carmelninja
2011-03-19 20:32:53
the smallest
the smallest
calvinhobbesliker
2011-03-19 20:32:53
The smallest one
The smallest one
iamthygod!!!!!!
2011-03-19 20:32:53
smallest
smallest
mathcountsloser
2011-03-19 20:32:53
Smallest.
Smallest.
etude
2011-03-19 20:32:53
smallest.
smallest.
zero.destroyer
2011-03-19 20:32:53
smallest
smallest
Kinata12
2011-03-19 20:32:58
The smallest, it doesn't have any overlaps
The smallest, it doesn't have any overlaps
JSGandora
2011-03-19 20:32:58
We want the smallest.
We want the smallest.
rrusczyk
2011-03-19 20:33:03
It looks like we maximize h by choosing b and c to be the smallest lengths of the triangle. But we have to be careful. We actually want the smallest of these three heights. If the height of the table is larger than h_A, for example, it will cause the folds corresponding to h_A to overlap, since h_A is the greatest the height can be to prevent those folds from overlapping. So, the height of the table can be no greater than the smallest of these three expressions.
It looks like we maximize h by choosing b and c to be the smallest lengths of the triangle. But we have to be careful. We actually want the smallest of these three heights. If the height of the table is larger than h_A, for example, it will cause the folds corresponding to h_A to overlap, since h_A is the greatest the height can be to prevent those folds from overlapping. So, the height of the table can be no greater than the smallest of these three expressions.
rrusczyk
2011-03-19 20:33:23
The minimum of these three expressions occurs when we have the longest sides in the denominator.
The minimum of these three expressions occurs when we have the longest sides in the denominator.
rrusczyk
2011-03-19 20:33:41
So, how do we finish?
So, how do we finish?
GoldenFrog1618
2011-03-19 20:34:23
2K/57
2K/57
Spring
2011-03-19 20:34:23
2K/57, use Heron's to find K
2K/57, use Heron's to find K
Cortana
2011-03-19 20:34:23
2K/57
2K/57
.cpp
2011-03-19 20:34:23
2K/(27+30) gives 2K/57 is the maximum height.
2K/(27+30) gives 2K/57 is the maximum height.
rrusczyk
2011-03-19 20:34:30
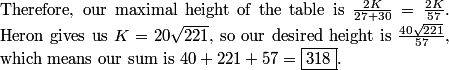
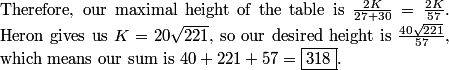
rrusczyk
2011-03-19 20:34:55
All right, we'll take a short break to rest my fingers :)
All right, we'll take a short break to rest my fingers :)
mathcountsloser
2011-03-19 20:36:07
That was hard. Do you think elementary geometry covers this?
That was hard. Do you think elementary geometry covers this?
ahaanomegas
2011-03-19 20:36:07
Was there an easier way to do that one?
Was there an easier way to do that one?
rrusczyk
2011-03-19 20:36:18
I don't think you'll see this in a typical geometry class!
I don't think you'll see this in a typical geometry class!
rrusczyk
2011-03-19 20:36:27
I don't think there's really an easier way to do this.
I don't think there's really an easier way to do this.
mathepic
2011-03-19 20:37:03
my school doesn't discuss how to do anything past 5 on an AMC...
my school doesn't discuss how to do anything past 5 on an AMC...
rrusczyk
2011-03-19 20:37:11
That's why we started AoPS :)
That's why we started AoPS :)
Jasmine8925
2011-03-19 20:37:54
haha my school doesn't discuss anything that would ever be on any math competition
haha my school doesn't discuss anything that would ever be on any math competition
mathcountsloser
2011-03-19 20:37:55
My school doesn't discuss anything.
My school doesn't discuss anything.
rrusczyk
2011-03-19 20:38:08
All right, back to work. Er, fun.
All right, back to work. Er, fun.
rrusczyk
2011-03-19 20:38:12
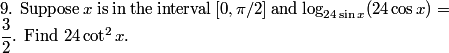
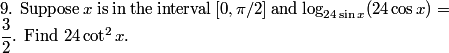
rrusczyk
2011-03-19 20:38:23
Where do we start
Where do we start
BOGTRO
2011-03-19 20:38:43
(24sinx)^3/2=24cosx
(24sinx)^3/2=24cosx
ahaanomegas
2011-03-19 20:38:43
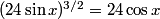
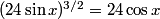
fortenforge
2011-03-19 20:38:43
get rid of the log
get rid of the log
superpi83
2011-03-19 20:38:43
convert to exponential form first
convert to exponential form first
Titandrake
2011-03-19 20:38:43
expand the log
expand the log
vcez
2011-03-19 20:38:43
put log in exp form
put log in exp form
GeorgiaTechMan
2011-03-19 20:38:43
(24sinx)^3/2=24cosx
(24sinx)^3/2=24cosx
tan90
2011-03-19 20:38:43
Exponential form
Exponential form
delta1
2011-03-19 20:38:43
get rid of the logs
get rid of the logs
Potential5
2011-03-19 20:38:46
unlog it
unlog it
rrusczyk
2011-03-19 20:39:00
unlog. Wonderful. My vocabulary has just expanded by one word.
unlog. Wonderful. My vocabulary has just expanded by one word.
rrusczyk
2011-03-19 20:39:04
We start by getting rid of the logarithm, and writing the equation in exponential form:
We start by getting rid of the logarithm, and writing the equation in exponential form:
rrusczyk
2011-03-19 20:39:09
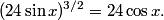
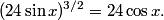
eb8368
2011-03-19 20:39:28
Square both sides
Square both sides
tan90
2011-03-19 20:39:28
Now square both sides.
Now square both sides.
GoldenFrog1618
2011-03-19 20:39:31
square
square
VIPMaster
2011-03-19 20:39:31
square it!!!
square it!!!
hrithikguy
2011-03-19 20:39:31
square both sides
square both sides
vcez
2011-03-19 20:39:31
square both sides
square both sides
pi091997
2011-03-19 20:39:31
square both sides?
square both sides?
fortenforge
2011-03-19 20:39:31
I squared both sides here
I squared both sides here
hsm174
2011-03-19 20:39:38
move the 24 to the lhs
move the 24 to the lhs
calvinhobbesliker
2011-03-19 20:39:38
Square both sides and divide by 24^2
Square both sides and divide by 24^2
rrusczyk
2011-03-19 20:39:45
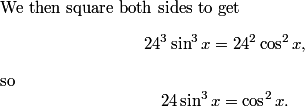
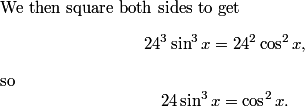
mathcountsloser
2011-03-19 20:39:52
this seems to be getting easier by the moment
this seems to be getting easier by the moment
rrusczyk
2011-03-19 20:39:56
That's the goal.
That's the goal.
policecap
2011-03-19 20:40:01
cos^2 = 1-sin^2
cos^2 = 1-sin^2
GeorgiaTechMan
2011-03-19 20:40:01
cosx=1-sin^2x
cosx=1-sin^2x
Cortana
2011-03-19 20:40:03
replace cos^2(x) with 1-sin^2(x)
replace cos^2(x) with 1-sin^2(x)
esque
2011-03-19 20:40:07
substitue 1-sin^x for cos^x
substitue 1-sin^x for cos^x
alanzee
2011-03-19 20:40:07
cos^2 x=1-sin^2 x
cos^2 x=1-sin^2 x
rrusczyk
2011-03-19 20:40:12
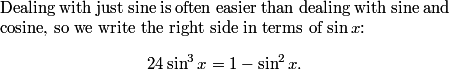
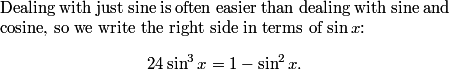
etude
2011-03-19 20:40:23
cos^2 x = 1 - sin^2 x. Substitute y = sin x and solve for y.
cos^2 x = 1 - sin^2 x. Substitute y = sin x and solve for y.
ahaanomegas
2011-03-19 20:40:24
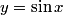
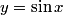
fortenforge
2011-03-19 20:40:28
Now write sin x = y,
Now write sin x = y,
rrusczyk
2011-03-19 20:40:32
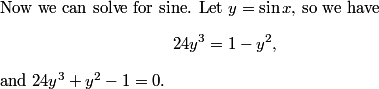
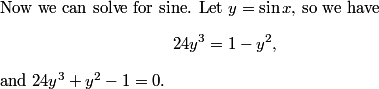
ahaanomegas
2011-03-19 20:40:34
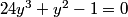
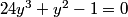
pinkmuskrat
2011-03-19 20:40:45
for the cubic in sin x, 1/3 is a root
for the cubic in sin x, 1/3 is a root
kangchangood
2011-03-19 20:40:45
then we test.. the value 1/3
then we test.. the value 1/3
adalander
2011-03-19 20:40:45
And can we factor this?
And can we factor this?
mathepic
2011-03-19 20:40:45
IIRC y = 3
IIRC y = 3
theone142857
2011-03-19 20:40:45
y=1/3 by rational root:whistle:
y=1/3 by rational root:whistle:
pinkmuskrat
2011-03-19 20:40:45
1/3 is a root
1/3 is a root
Z91
2011-03-19 20:40:45
y=1/3
y=1/3
SuperNerd123
2011-03-19 20:40:52
y=1/3 Rational Root therom
y=1/3 Rational Root therom
professordad
2011-03-19 20:40:52
rational root theorem, y = 1/3 happens to work'
rational root theorem, y = 1/3 happens to work'
rrusczyk
2011-03-19 20:40:55
We don't know for sure yet that (sin x) must be rational, but we check for that just in case. From the Rational Root Theorem and the fact that y is positive (since x is between 0 and pi/2), we know that we only have to test fractions of the form 1/n, where n divides 24, for y. We quickly find that y=1/3 works, and we have the factorization
We don't know for sure yet that (sin x) must be rational, but we check for that just in case. From the Rational Root Theorem and the fact that y is positive (since x is between 0 and pi/2), we know that we only have to test fractions of the form 1/n, where n divides 24, for y. We quickly find that y=1/3 works, and we have the factorization
rrusczyk
2011-03-19 20:40:58
(3y-1)(8y^2+3y +1) = 0
(3y-1)(8y^2+3y +1) = 0
rrusczyk
2011-03-19 20:41:03
The quadratic has no positive roots, so we know that sin x = 1/3.
The quadratic has no positive roots, so we know that sin x = 1/3.
rrusczyk
2011-03-19 20:41:06
Now, we just have to find 24cot^2x. How do we finish?
Now, we just have to find 24cot^2x. How do we finish?
Cortana
2011-03-19 20:41:50
find cos^2(x)
find cos^2(x)
Cortana
2011-03-19 20:41:50
cot^2(X)=cos^2(x)/sin^2(x)
cot^2(X)=cos^2(x)/sin^2(x)
tan90
2011-03-19 20:41:53
Find cos^2 (x)
Find cos^2 (x)
rrusczyk
2011-03-19 20:42:01
OK, finish it off.
OK, finish it off.
rrusczyk
2011-03-19 20:42:35
There are a ton of ways to finish from here:
There are a ton of ways to finish from here:
eb8368
2011-03-19 20:42:38
24cot^2x = 24(1-sin^2x)/(sin^2x)
24cot^2x = 24(1-sin^2x)/(sin^2x)
Spring
2011-03-19 20:42:38
24cot^2x=24(cos2^x/sin^2x)=24^2sinx=24^2/3=192
24cot^2x=24(cos2^x/sin^2x)=24^2sinx=24^2/3=192
calvinhobbesliker
2011-03-19 20:42:38
cos^2=8/9; sin^2=1/9 Answer is thus 24*8
cos^2=8/9; sin^2=1/9 Answer is thus 24*8
Z91
2011-03-19 20:42:38
Since 24sin^3(x)=cos^2(x), cot(x)=24sin(x) and 24cot(x)=576sin(x)
Since 24sin^3(x)=cos^2(x), cot(x)=24sin(x) and 24cot(x)=576sin(x)
policecap
2011-03-19 20:42:48
alanzee
2011-03-19 20:42:58
24(1/3)sin^2 x=cos^2 x =>24cos^2 x/sin^2x=192
24(1/3)sin^2 x=cos^2 x =>24cos^2 x/sin^2x=192
ahaanomegas
2011-03-19 20:42:58
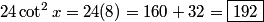
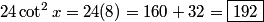
etude
2011-03-19 20:43:01
cot^2 x = (8/3)/(1/3) = 8. 8*24 = 192 answer.
cot^2 x = (8/3)/(1/3) = 8. 8*24 = 192 answer.
rrusczyk
2011-03-19 20:43:06
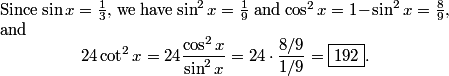
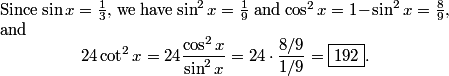
billybob42
2011-03-19 20:43:12
i got scared by the cubic. is there an easier way to solve this?
i got scared by the cubic. is there an easier way to solve this?
rrusczyk
2011-03-19 20:43:43
The first time I did it, I converted everything to cotangent, and you get a cubic with an integer root, which is less scary (and was simpler to see the solution.)
The first time I did it, I converted everything to cotangent, and you get a cubic with an integer root, which is less scary (and was simpler to see the solution.)
rrusczyk
2011-03-19 20:43:58
But, this problem was particularly guessable: we might have guessed that 24 sin x and 24 cos x need be rational powers of either 2 or 3, and then just tried values of sin x with 3 or 8 as the denominator. 3 seems like a better first guess, and trying 1/3 gets you to the answer right away!
But, this problem was particularly guessable: we might have guessed that 24 sin x and 24 cos x need be rational powers of either 2 or 3, and then just tried values of sin x with 3 or 8 as the denominator. 3 seems like a better first guess, and trying 1/3 gets you to the answer right away!
rrusczyk
2011-03-19 20:44:31
In almost every AIME, there is a problem from 7 to 12 that has lots of notation (logs, trig, floor function) that turns out to be way easier than it looks.
In almost every AIME, there is a problem from 7 to 12 that has lots of notation (logs, trig, floor function) that turns out to be way easier than it looks.
GoldenFrog1618
2011-03-19 20:44:47
how do you convert sin^3x/cos^2 x to cot?
how do you convert sin^3x/cos^2 x to cot?
rrusczyk
2011-03-19 20:45:12
I started with the cot^2 + 1 = csc^2 identity.
I started with the cot^2 + 1 = csc^2 identity.
rrusczyk
2011-03-19 20:46:03


rrusczyk
2011-03-19 20:46:33
Rather than going after obtuse, what might we go after?
Rather than going after obtuse, what might we go after?
rdj5933mile5
2011-03-19 20:47:01
Consider probability of finding acute triangle or right?
Consider probability of finding acute triangle or right?
pinkmuskrat
2011-03-19 20:47:01
right and acute
right and acute
pi.guy3.14
2011-03-19 20:47:01
right and acute?
right and acute?
Spring
2011-03-19 20:47:01
right or acute
right or acute
adalander
2011-03-19 20:47:05
Right or acute?
Right or acute?
rrusczyk
2011-03-19 20:47:08
When I did this problem, my first thought was to do the complement: find n such that the probability that a random triangle is acute or right is 32/125. (Because 32/125 is a smaller number, so perhaps easier.)
When I did this problem, my first thought was to do the complement: find n such that the probability that a random triangle is acute or right is 32/125. (Because 32/125 is a smaller number, so perhaps easier.)
skyhog
2011-03-19 20:47:17
Break into cases: n is odd or n is even
Break into cases: n is odd or n is even
calvinhobbesliker
2011-03-19 20:47:17
Casework with n even and odd?
Casework with n even and odd?
rrusczyk
2011-03-19 20:47:22
We can only get a right angle if n is even (so that one of the sides of the triangle is a diameter).
We can only get a right angle if n is even (so that one of the sides of the triangle is a diameter).
rrusczyk
2011-03-19 20:47:25
This suggests we may have to look at the odd and even cases separately.
This suggests we may have to look at the odd and even cases separately.
rrusczyk
2011-03-19 20:47:33
So let's do the odd case first. We let n = 2k+1 for some positive k.
So let's do the odd case first. We let n = 2k+1 for some positive k.
rrusczyk
2011-03-19 20:47:57
What might we do as a first step to simplify thinking about the problem?
What might we do as a first step to simplify thinking about the problem?
calvinhobbesliker
2011-03-19 20:48:28
Fix a vertex
Fix a vertex
soulspeedy
2011-03-19 20:48:28
fix a point on the figure
fix a point on the figure
rrusczyk
2011-03-19 20:48:31
We can arbitrarily choose the first vertex to be any vertex of the n-gon (by the rotational symmetry). Suppose for the sake of ease of discussion that it's the top vertex:
We can arbitrarily choose the first vertex to be any vertex of the n-gon (by the rotational symmetry). Suppose for the sake of ease of discussion that it's the top vertex:
rrusczyk
2011-03-19 20:48:35
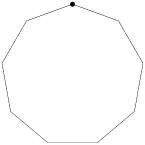

rrusczyk
2011-03-19 20:48:41
How many possible ways to complete the triangle?
How many possible ways to complete the triangle?
rrusczyk
2011-03-19 20:49:01
Remember, we are letting n = 2k+1 here.
Remember, we are letting n = 2k+1 here.
Spring
2011-03-19 20:49:29
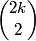
GeorgiaTechMan
2011-03-19 20:49:29
or (2k)C2
or (2k)C2
etude
2011-03-19 20:49:29
2k C 2
2k C 2
tiger21
2011-03-19 20:49:29
pick 2 from 2k
pick 2 from 2k
AlphaMath1
2011-03-19 20:49:29
(2k 2)
(2k 2)
pi091997
2011-03-19 20:49:29
C(2k,2)
C(2k,2)
centralbs
2011-03-19 20:49:29
(2k C 2)
(2k C 2)
rrusczyk
2011-03-19 20:49:40
We have to choose two of the remaining 2k vertices, so it's C(2k,2).
We have to choose two of the remaining 2k vertices, so it's C(2k,2).
rrusczyk
2011-03-19 20:49:44
How many ways to make an acute triangle?
How many ways to make an acute triangle?
kangchangood
2011-03-19 20:49:53
well... triangles that include that point.
well... triangles that include that point.
rrusczyk
2011-03-19 20:50:06
Right, triangles that include that point.
Right, triangles that include that point.
rrusczyk
2011-03-19 20:50:33
Remember that we are aiming at acute triangles here.
Remember that we are aiming at acute triangles here.
rrusczyk
2011-03-19 20:50:46
So, what do we know about the two other points?
So, what do we know about the two other points?
Kinata12
2011-03-19 20:51:00
The 2 points must be on opposite sides of the diameter
The 2 points must be on opposite sides of the diameter
rrusczyk
2011-03-19 20:51:05
We need one vertex from the left side and one from the right side. (For example, if both are from the left side, then the middle vertex there will give an obtuse triangle.)
We need one vertex from the left side and one from the right side. (For example, if both are from the left side, then the middle vertex there will give an obtuse triangle.)
rrusczyk
2011-03-19 20:51:15
Also, we need that the two new vertices are separated by no more than half the triangle.
Also, we need that the two new vertices are separated by no more than half the triangle.
rrusczyk
2011-03-19 20:51:26
So, in particular, if we pick the top vertex on the left, we must pick the bottom vertex on the right:
So, in particular, if we pick the top vertex on the left, we must pick the bottom vertex on the right:
rrusczyk
2011-03-19 20:51:30


rrusczyk
2011-03-19 20:51:44
What if we pick the second highest vertex on the left?
What if we pick the second highest vertex on the left?
VIPMaster
2011-03-19 20:52:31
the bottom vertex on the right or the one right above it
the bottom vertex on the right or the one right above it
rdj5933mile5
2011-03-19 20:52:31
2 choices
2 choices
rrusczyk
2011-03-19 20:52:35
If we pick the 2nd highest vertex on the left, we must pick one of the bottom two vertices on the right.
If we pick the 2nd highest vertex on the left, we must pick one of the bottom two vertices on the right.
rrusczyk
2011-03-19 20:52:38
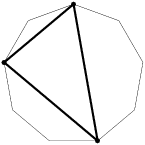

rrusczyk
2011-03-19 20:52:41
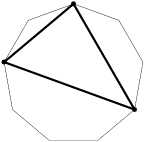

rrusczyk
2011-03-19 20:52:46
And so on...
And so on...
rrusczyk
2011-03-19 20:52:51
So how many acute triangles are there?
So how many acute triangles are there?
ahaanomegas
2011-03-19 20:53:20
But, in your diagram, you just arbitrarily picked the number of sides in the polygon, is that correct?
But, in your diagram, you just arbitrarily picked the number of sides in the polygon, is that correct?
rrusczyk
2011-03-19 20:53:27
Right, I want an answer in terms of k
Right, I want an answer in terms of k
skyhog
2011-03-19 20:53:31
k(k+1)/2
k(k+1)/2
etude
2011-03-19 20:53:32
k(k+1)/2?
k(k+1)/2?
rrusczyk
2011-03-19 20:53:37
As we pick a vertex from top to bottom on the left side, we have 1, 2, ..., k choices for a vertex on the right side.
As we pick a vertex from top to bottom on the left side, we have 1, 2, ..., k choices for a vertex on the right side.
rrusczyk
2011-03-19 20:53:40
So there are 1+2+...+k acute triangles.
So there are 1+2+...+k acute triangles.
rrusczyk
2011-03-19 20:53:46
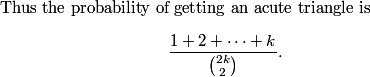
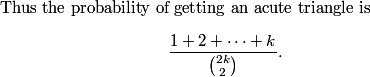
rrusczyk
2011-03-19 20:53:59
How does this simplify?
How does this simplify?
pinkmuskrat
2011-03-19 20:54:38
k(k+1)/2k(2k-1)
k(k+1)/2k(2k-1)
eb8368
2011-03-19 20:54:39
(k+1)/2(k-1)
(k+1)/2(k-1)
skyhog
2011-03-19 20:54:39
(k+1)/[2(2k-1)]
(k+1)/[2(2k-1)]
rdj5933mile5
2011-03-19 20:54:39
(k+1)/(4k-2)
(k+1)/(4k-2)
Spring
2011-03-19 20:54:42
(k+1)/(2(k-1))
(k+1)/(2(k-1))
rrusczyk
2011-03-19 20:54:45
The numerator is equal to (1/2)k(k+1).
The numerator is equal to (1/2)k(k+1).
rrusczyk
2011-03-19 20:54:48
The denominator is equal to (1/2)(2k)(2k-1).
The denominator is equal to (1/2)(2k)(2k-1).
rrusczyk
2011-03-19 20:54:52


policecap
2011-03-19 20:54:56
=32/125
=32/125
rrusczyk
2011-03-19 20:54:59
We want this to be equal to 32/125.
We want this to be equal to 32/125.
rrusczyk
2011-03-19 20:55:02
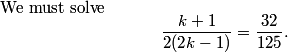
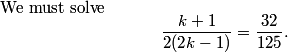
infinity1
2011-03-19 20:55:31
k=63
k=63
jeff10
2011-03-19 20:55:31
k=63
k=63
DystopianStriker
2011-03-19 20:55:31
k=63
k=63
calvinhobbesliker
2011-03-19 20:55:35
k=63?
k=63?
super_pi314
2011-03-19 20:55:35
63
63
ahaanomegas
2011-03-19 20:55:40
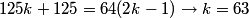
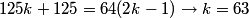
VIPMaster
2011-03-19 20:55:44
125k + 125 = 128k - 64 => k = 63
125k + 125 = 128k - 64 => k = 63
rrusczyk
2011-03-19 20:55:47
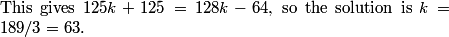
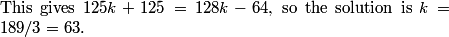
AlphaMath1
2011-03-19 20:56:16
BUT we need n
BUT we need n
tan90
2011-03-19 20:56:16
so n = 127
so n = 127
skyhog
2011-03-19 20:56:16
so n = 127
so n = 127
BarbieRocks
2011-03-19 20:56:20
so 2k+1=127
so 2k+1=127
ahaanomegas
2011-03-19 20:56:20
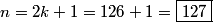
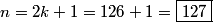
etude
2011-03-19 20:56:20
Thus n = 127
Thus n = 127
rrusczyk
2011-03-19 20:56:23
Recalling that n = 2k+1, we see that n = 2(63)+1 = 127 is a possible value.
Recalling that n = 2k+1, we see that n = 2(63)+1 = 127 is a possible value.
kangchangood
2011-03-19 20:56:25
there come even cases
there come even cases
rrusczyk
2011-03-19 20:56:28
Now the even case. Let n = 2k.
Now the even case. Let n = 2k.
rrusczyk
2011-03-19 20:56:32
Again, we can assume the first vertex picked is the "top" vertex. We can pick two other vertices in C(2k-1,2) ways.
Again, we can assume the first vertex picked is the "top" vertex. We can pick two other vertices in C(2k-1,2) ways.
rrusczyk
2011-03-19 20:56:38
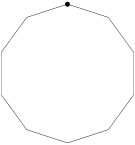

Jasmine8925
2011-03-19 20:57:17
if we pick the bottom vertex, any other vertex we pick will make a right triangle
if we pick the bottom vertex, any other vertex we pick will make a right triangle
rrusczyk
2011-03-19 20:57:21
If we have the opposite vertex, then we can pick any of the other 2k-2 vertices and get a right triangle.
If we have the opposite vertex, then we can pick any of the other 2k-2 vertices and get a right triangle.
rrusczyk
2011-03-19 20:57:29
Otherwise, we have one from the left side and one from the right side (just like in the odd case).
Otherwise, we have one from the left side and one from the right side (just like in the odd case).
rrusczyk
2011-03-19 20:57:51
OK, so what is the number of acute or right triangles we get in this case?
OK, so what is the number of acute or right triangles we get in this case?
etude
2011-03-19 20:59:25
2k-2 + k(k-1)/2?
2k-2 + k(k-1)/2?
.cpp
2011-03-19 20:59:25
(k-1)k/2 + 2k-2.
(k-1)k/2 + 2k-2.
rrusczyk
2011-03-19 20:59:39
And also as in the odd case, if we take the top vertex on the left, we must take the bottom vertex on the right; if we take the next highest vertex on the left, we must take one of the 2 bottom vertices on the right, and so on.
And also as in the odd case, if we take the top vertex on the left, we must take the bottom vertex on the right; if we take the next highest vertex on the left, we must take one of the 2 bottom vertices on the right, and so on.
rrusczyk
2011-03-19 20:59:57
So there are 1 + 2 + ... + (k-1) ways to take a vertex from either side and get an acute or right triangle. We put these together with the 2k-2 that we already found.
So there are 1 + 2 + ... + (k-1) ways to take a vertex from either side and get an acute or right triangle. We put these together with the 2k-2 that we already found.
rrusczyk
2011-03-19 21:00:03
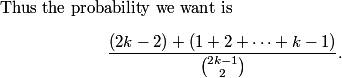
rrusczyk
2011-03-19 21:00:11
And how does this sample?
And how does this sample?
rrusczyk
2011-03-19 21:00:18
simplify?
simplify?
professordad
2011-03-19 21:01:27
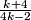
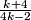
rdj5933mile5
2011-03-19 21:01:27
(k+4)/(4k-2)
(k+4)/(4k-2)
DystopianStriker
2011-03-19 21:01:27
(k+4)/2(2k-1)?
(k+4)/2(2k-1)?
policecap
2011-03-19 21:01:27
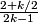
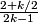
rrusczyk
2011-03-19 21:01:30
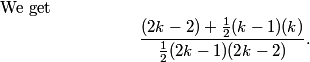
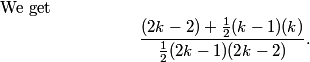
rrusczyk
2011-03-19 21:01:34
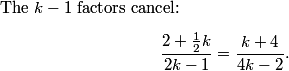
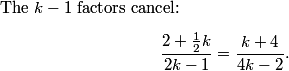
rrusczyk
2011-03-19 21:01:37
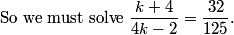
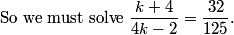
policecap
2011-03-19 21:02:24
k=188
k=188
DystopianStriker
2011-03-19 21:02:24
188
188
jeff10
2011-03-19 21:02:24
k=188
k=188
super_pi314
2011-03-19 21:02:24
188
188
ahaanomegas
2011-03-19 21:02:30
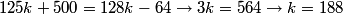
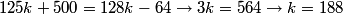
VIPMaster
2011-03-19 21:02:30
125k + 500 = 128k - 64 => k = 188
125k + 500 = 128k - 64 => k = 188
rrusczyk
2011-03-19 21:02:32
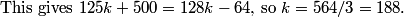
policecap
2011-03-19 21:02:52
376 is a solution
so our answer is 127+376=503
376 is a solution
so our answer is 127+376=503
ahaanomegas
2011-03-19 21:02:52
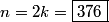
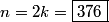
kangchangood
2011-03-19 21:02:52
then n
then n
prezcoin
2011-03-19 21:02:52
n= 376
n= 376
icecreamcakepie
2011-03-19 21:02:52
n=2K
n=2K
VIPMaster
2011-03-19 21:02:58
n = 188*2 = 376
n = 188*2 = 376
.cpp
2011-03-19 21:02:58
2k = 376, so our answer is 376+127 = 503.
2k = 376, so our answer is 376+127 = 503.
rrusczyk
2011-03-19 21:03:00
This yields n = 2k = 376 as our other possible value.
This yields n = 2k = 376 as our other possible value.
rrusczyk
2011-03-19 21:03:06
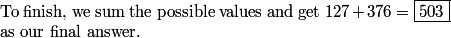
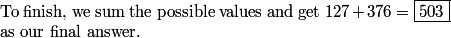
RobRoobiks
2011-03-19 21:03:14
is there a way to count obtuse triangles?
is there a way to count obtuse triangles?
rrusczyk
2011-03-19 21:03:23
Sure! See if you can find one on your own.
Sure! See if you can find one on your own.
rrusczyk
2011-03-19 21:03:40
(There are probably discussions about it on the message board. It will look a lot like this one.
(There are probably discussions about it on the message board. It will look a lot like this one.
rrusczyk
2011-03-19 21:03:49
All right. We've rounded the turn!
All right. We've rounded the turn!
rrusczyk
2011-03-19 21:03:51
5 more to go.
5 more to go.
rrusczyk
2011-03-19 21:03:56


rrusczyk
2011-03-19 21:04:26
The "divided by 1000" appearing twice suggests what?
The "divided by 1000" appearing twice suggests what?
jeff10
2011-03-19 21:04:37
mod1000 basically
mod1000 basically
Lemon123
2011-03-19 21:04:37
mod 1000
mod 1000
pi.guy3.14
2011-03-19 21:04:37
mod 1000
mod 1000
Jasmine8925
2011-03-19 21:04:37
mod 1000
mod 1000
policecap
2011-03-19 21:04:37
mod 1000
mod 1000
prezcoin
2011-03-19 21:04:37
mod 1000
mod 1000
rrusczyk
2011-03-19 21:04:39
We probably want to be working mod 1000.
We probably want to be working mod 1000.
rrusczyk
2011-03-19 21:04:44
So we want to determine all the different residues of 2^n mod 1000 and then add them up mod 1000.
So we want to determine all the different residues of 2^n mod 1000 and then add them up mod 1000.
rrusczyk
2011-03-19 21:05:12
What observations should we start with?
What observations should we start with?
.cpp
2011-03-19 21:05:25
All remainders are multiples of 8, except for 1, 2, and 4.
All remainders are multiples of 8, except for 1, 2, and 4.
prezcoin
2011-03-19 21:05:35
after 1,2,4, the rest of the numbers are divisible by 8, as is 1000
after 1,2,4, the rest of the numbers are divisible by 8, as is 1000
carmelninja
2011-03-19 21:05:40
we actually only really need to consider it mod125
we actually only really need to consider it mod125
ahaanomegas
2011-03-19 21:05:45
All remainders are multiples of 8, except for 1, 2, and 4
All remainders are multiples of 8, except for 1, 2, and 4
rdj5933mile5
2011-03-19 21:05:47
work mod 125?
work mod 125?
rrusczyk
2011-03-19 21:05:53
Often with mods, we break up the modulus into its prime power components.
Often with mods, we break up the modulus into its prime power components.
rrusczyk
2011-03-19 21:05:56
So we can look separately as residues mod 8 and mod 125.
So we can look separately as residues mod 8 and mod 125.
rrusczyk
2011-03-19 21:05:59
Mod 8 is easy: the powers start 1,2,4, and then all the rest of the powers are multiples of 8.
Mod 8 is easy: the powers start 1,2,4, and then all the rest of the powers are multiples of 8.
rrusczyk
2011-03-19 21:06:08
So our sum looks like 1 + 2 + 4 + 8(1+2+4+...), and we need to analyze the sum inside the parentheses mod 125.
So our sum looks like 1 + 2 + 4 + 8(1+2+4+...), and we need to analyze the sum inside the parentheses mod 125.
ahaanomegas
2011-03-19 21:06:11
Why 125?
Why 125?
soulspeedy
2011-03-19 21:06:13
note that 1000=2^3*5^3
note that 1000=2^3*5^3
rrusczyk
2011-03-19 21:06:26
But what do we know about that sum in parentheses there?
But what do we know about that sum in parentheses there?
Jasmine8925
2011-03-19 21:06:58
geometric series
geometric series
VIPMaster
2011-03-19 21:06:58
its a geometric series!
its a geometric series!
calvinhobbesliker
2011-03-19 21:06:58
It's 2^n-1
It's 2^n-1
eb8368
2011-03-19 21:06:58
It cycles after 2^100
It cycles after 2^100
RelaxationUtopia
2011-03-19 21:06:58
Geometric sequence?
Geometric sequence?
rrusczyk
2011-03-19 21:07:06
It is indeed a geometric series.
It is indeed a geometric series.
VIPMaster
2011-03-19 21:07:27
i like eb8368's observation better
i like eb8368's observation better
rrusczyk
2011-03-19 21:07:44
We care about the sum mod 125 (we'll multiply the result by 8 after that to get the sum mod 1000).
We care about the sum mod 125 (we'll multiply the result by 8 after that to get the sum mod 1000).
rrusczyk
2011-03-19 21:07:52
Now, eb's observation is interesting.
Now, eb's observation is interesting.
centralbs
2011-03-19 21:07:54
How do you know it cycles after 2^100?
How do you know it cycles after 2^100?
rrusczyk
2011-03-19 21:08:03
We could use the Euler-Fermat Theorem, which tells us that because 2 and 125 are relatively prime, we have 2^100 = 1 (mod 125). But we don't even need such a fancy theorem. We know for sure that the powers of 2 mod 125 will eventually repeat, since there are infinitely many powers of 2. So, we'll get 2^a = 2^b (mod 125) with a>b at some point. Then, because 2 and 125 are relatively prime, we have 2^(a-b) = 1 (mod 125).
We could use the Euler-Fermat Theorem, which tells us that because 2 and 125 are relatively prime, we have 2^100 = 1 (mod 125). But we don't even need such a fancy theorem. We know for sure that the powers of 2 mod 125 will eventually repeat, since there are infinitely many powers of 2. So, we'll get 2^a = 2^b (mod 125) with a>b at some point. Then, because 2 and 125 are relatively prime, we have 2^(a-b) = 1 (mod 125).
rrusczyk
2011-03-19 21:08:37
We don't necessarily need to know 2^100 = 1; it's enough to know that 2^k = 1 (mod 125) for some k. Why is this useful? That is, why is it important that it will repeat mod 125?
We don't necessarily need to know 2^100 = 1; it's enough to know that 2^k = 1 (mod 125) for some k. Why is this useful? That is, why is it important that it will repeat mod 125?
jeff10
2011-03-19 21:09:35
2^100 is not 1.
2^100 is not 1.
rrusczyk
2011-03-19 21:09:41
That's mod 125...
That's mod 125...
eb8368
2011-03-19 21:09:49
2^k = 2^(k+1) - 1
2^k = 2^(k+1) - 1
etude
2011-03-19 21:09:49
Therefore, that series is 2^k - 1 which is 0 mod 125. Thus the sum is 7 mod 125.
Therefore, that series is 2^k - 1 which is 0 mod 125. Thus the sum is 7 mod 125.
.cpp
2011-03-19 21:09:49
Sum in parenthesis is 2^k - 1 = 0 mod 125.
Sum in parenthesis is 2^k - 1 = 0 mod 125.
rrusczyk
2011-03-19 21:09:58
Exactly.
Exactly.
rrusczyk
2011-03-19 21:10:02
Because when we hit 2^k, our sum will repeat mod 125, and thus repeat mod 1000.
Because when we hit 2^k, our sum will repeat mod 125, and thus repeat mod 1000.
rrusczyk
2011-03-19 21:10:07
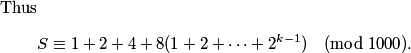
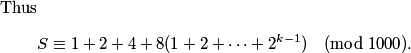
rrusczyk
2011-03-19 21:10:20
All we are using here is the fact that this sum will repeat at some point mod 125.
All we are using here is the fact that this sum will repeat at some point mod 125.
rrusczyk
2011-03-19 21:10:28
We don't even care where!
We don't even care where!
rrusczyk
2011-03-19 21:10:37
As noted before, the expression is a geometric series.
As noted before, the expression is a geometric series.
rrusczyk
2011-03-19 21:10:40
It's equal to 2^k - 1.
It's equal to 2^k - 1.
rrusczyk
2011-03-19 21:10:43
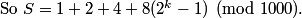
Titandrake
2011-03-19 21:10:45
that is pretty tricky
that is pretty tricky
mathcountsloser
2011-03-19 21:10:52
nice
nice
centralbs
2011-03-19 21:10:53
ooo wow thats soo clever
ooo wow thats soo clever
rrusczyk
2011-03-19 21:11:06
Yes, very tricky (DPatrick came up with this; I can't claim credit...)
Yes, very tricky (DPatrick came up with this; I can't claim credit...)
Titandrake
2011-03-19 21:11:19
so then 2^k -1 = 0 mod 125, so 8 times that is 0 mod 1000
so then 2^k -1 = 0 mod 125, so 8 times that is 0 mod 1000
rrusczyk
2011-03-19 21:11:21
2^k = 1 (mod 125), so 2^k - 1 is a multiple of 125.
2^k = 1 (mod 125), so 2^k - 1 is a multiple of 125.
rrusczyk
2011-03-19 21:11:30
Thus 8(2^k - 1) is a multiple of 1000, and hence goes away mod 1000.
Thus 8(2^k - 1) is a multiple of 1000, and hence goes away mod 1000.
VIPMaster
2011-03-19 21:11:35
then we get 1 + 2 + 4 + 0 = 7
then we get 1 + 2 + 4 + 0 = 7
hchen023
2011-03-19 21:11:35
so S = 1 + 2 + 4 + 0 = 007?
so S = 1 + 2 + 4 + 0 = 007?
jeff10
2011-03-19 21:11:40
that means that S is congruent to 7 (mod 1000)
that means that S is congruent to 7 (mod 1000)
soulspeedy
2011-03-19 21:11:40
so our answer is 1+2+4=7
so our answer is 1+2+4=7
DystopianStriker
2011-03-19 21:11:53
1+2+4=7
1+2+4=7
ahaanomegas
2011-03-19 21:11:53
007
007
tan90
2011-03-19 21:11:53
James Bond... 007
James Bond... 007
girishvar12
2011-03-19 21:11:53
$007$
$007$
mathcountsloser
2011-03-19 21:11:53
007 = james bond
007 = james bond
eb8368
2011-03-19 21:11:53
S= 007
S= 007
rrusczyk
2011-03-19 21:11:56
So we're left with just S = 1 + 2 + 4 (mod 1000) = 7 (mod 1000).
So we're left with just S = 1 + 2 + 4 (mod 1000) = 7 (mod 1000).
rrusczyk
2011-03-19 21:12:00


rrusczyk
2011-03-19 21:12:13
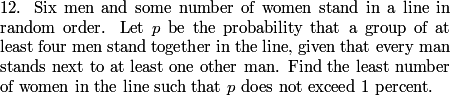
rrusczyk
2011-03-19 21:12:33
So, what do we have to do here?
So, what do we have to do here?
.cpp
2011-03-19 21:12:52
Probability = desired/total possibilities.
Probability = desired/total possibilities.
ahaanomegas
2011-03-19 21:13:02
P = desired/total
P = desired/total
jeff10
2011-03-19 21:13:17
P=desired/total possible
P=desired/total possible
rrusczyk
2011-03-19 21:13:19
We treat this as a usual "desired/possible" counting probability problem.
We treat this as a usual "desired/possible" counting probability problem.
ksun48
2011-03-19 21:13:27
casework?
casework?
AlphaMath1
2011-03-19 21:13:27
Start caseworking?
Start caseworking?
calvinhobbesliker
2011-03-19 21:13:27
Split into cases
Split into cases
rrusczyk
2011-03-19 21:13:46
And we'll have to break into careful casework.
And we'll have to break into careful casework.
rrusczyk
2011-03-19 21:13:50
rrusczyk
2011-03-19 21:13:54
Let's list the cases. If every man must be next to another man, what types of configurations can we have?
Let's list the cases. If every man must be next to another man, what types of configurations can we have?
policecap
2011-03-19 21:15:05
2/2/2, 2/4, 3/3, 4/2, 6
2/2/2, 2/4, 3/3, 4/2, 6
carmelninja
2011-03-19 21:15:05
2-2-2, 2-4, 3-3, 4-2, 6
2-2-2, 2-4, 3-3, 4-2, 6
rrusczyk
2011-03-19 21:15:07
Notice that there are two with a 4 and a 2!
Notice that there are two with a 4 and a 2!
rrusczyk
2011-03-19 21:15:15
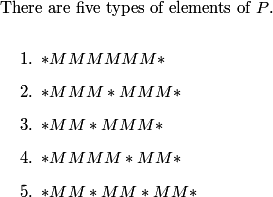
rrusczyk
2011-03-19 21:15:24
Each asterisk represents some unknown number of women.
Each asterisk represents some unknown number of women.
rrusczyk
2011-03-19 21:15:29
Now we need a variable. Let w be the number of women.
Now we need a variable. Let w be the number of women.
rrusczyk
2011-03-19 21:15:41
OK, how do we could the first case?
OK, how do we could the first case?
willwang123
2011-03-19 21:15:53
3rd case?
3rd case?
Kinata12
2011-03-19 21:15:53
You drew #3 wrong
You drew #3 wrong
rrusczyk
2011-03-19 21:16:06
The invisible man is in that group. Look closely.
The invisible man is in that group. Look closely.
rrusczyk
2011-03-19 21:16:17
How do we count the first case?
How do we count the first case?
mthcz11
2011-03-19 21:16:21
omg! i c him!!!
omg! i c him!!!
rrusczyk
2011-03-19 21:16:25
That's better
That's better
rrusczyk
2011-03-19 21:16:39
How do we could the first case
How do we could the first case
ksun48
2011-03-19 21:16:47
w+1 because there does not need to be a man in each *
w+1 because there does not need to be a man in each *
.cpp
2011-03-19 21:16:47
(w+1 choose 1) possibilities.
(w+1 choose 1) possibilities.
rrusczyk
2011-03-19 21:16:55
There are w+1 slots for the men to take (including the ends), so there are w+1 such arrangements.
There are w+1 slots for the men to take (including the ends), so there are w+1 such arrangements.
rrusczyk
2011-03-19 21:17:12
(We first line the women up from 1 to w)
(We first line the women up from 1 to w)
rrusczyk
2011-03-19 21:17:19
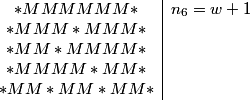
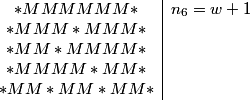
rrusczyk
2011-03-19 21:17:22
How many ways can we place *MMM*MMM*?
How many ways can we place *MMM*MMM*?
centralbs
2011-03-19 21:17:35
Are we counting the men as indistinguishable?
Are we counting the men as indistinguishable?
rrusczyk
2011-03-19 21:17:37
Yes.
Yes.
rrusczyk
2011-03-19 21:17:44
Way easier that way!
Way easier that way!
Jasmine8925
2011-03-19 21:17:50
what's w?
what's w?
rrusczyk
2011-03-19 21:17:54
Number of women
Number of women
rrusczyk
2011-03-19 21:18:30
We line them up and then put the men in the line afterwards. How many ways can we tackle the *MMM*MMM* case?
We line them up and then put the men in the line afterwards. How many ways can we tackle the *MMM*MMM* case?
etude
2011-03-19 21:18:53
w+1 C 2
w+1 C 2
Kinata12
2011-03-19 21:18:53
w(w+1)/2
w(w+1)/2
rrusczyk
2011-03-19 21:18:57
We need to pick two of these w+1 slots in the line of w women (including the ends!).
We need to pick two of these w+1 slots in the line of w women (including the ends!).
rrusczyk
2011-03-19 21:19:09
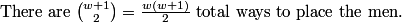
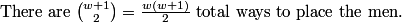
rrusczyk
2011-03-19 21:19:15
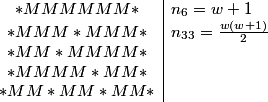
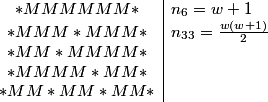
rrusczyk
2011-03-19 21:19:24
How about the next case?
How about the next case?
pi.guy3.14
2011-03-19 21:19:49
the next two are the same
the next two are the same
policecap
2011-03-19 21:19:49
same thing
same thing
ParallelProcess
2011-03-19 21:19:49
and then that applies for the next two as well
and then that applies for the next two as well
GoldenFrog1618
2011-03-19 21:19:49
same
same
VIPMaster
2011-03-19 21:19:49
same as the last one
same as the last one
Kinata12
2011-03-19 21:19:49
The same, w+1C2
The same, w+1C2
Lemon123
2011-03-19 21:19:49
same
same
tan90
2011-03-19 21:19:56
Same as case 2
Same as case 2
eb8368
2011-03-19 21:19:56
w+1 C 2
w+1 C 2
rrusczyk
2011-03-19 21:19:58
We know that n_24 and n_42 must be equal to n_33 since it's the same computation:
We know that n_24 and n_42 must be equal to n_33 since it's the same computation:
rrusczyk
2011-03-19 21:20:02
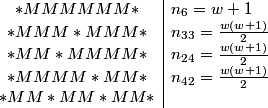
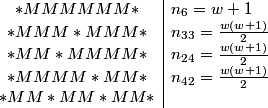
rrusczyk
2011-03-19 21:20:11
And the last case?
And the last case?
Jasmine8925
2011-03-19 21:20:22
the last case is w+1 C 3
the last case is w+1 C 3
policecap
2011-03-19 21:20:23
n+1 C 3
n+1 C 3
etude
2011-03-19 21:20:23
The last one is w+1 C 3.
The last one is w+1 C 3.
VIPMaster
2011-03-19 21:20:23
w + 1 choose 3
w + 1 choose 3
dlennon
2011-03-19 21:20:26
C(w+1,3)
C(w+1,3)
Kinata12
2011-03-19 21:20:26
w+1C3
w+1C3
rdj5933mile5
2011-03-19 21:20:26
w+1c3
w+1c3
rrusczyk
2011-03-19 21:20:28
We need to place three groups of men. There are C(w+1,3) ways to place these groups.
We need to place three groups of men. There are C(w+1,3) ways to place these groups.
rrusczyk
2011-03-19 21:20:31
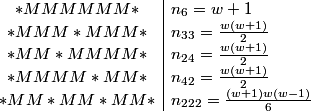
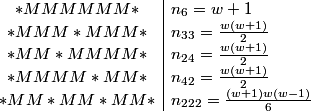
rrusczyk
2011-03-19 21:20:41
Now what is p?
Now what is p?
VIPMaster
2011-03-19 21:20:55
the sum of all of these
the sum of all of these
kangchangood
2011-03-19 21:20:55
sum?
sum?
vcez
2011-03-19 21:20:55
probability is desired over total
probability is desired over total
aerrowfinn72
2011-03-19 21:20:57
add it all up
add it all up
rrusczyk
2011-03-19 21:21:06
We add all of these, and that gives the denominator.
We add all of these, and that gives the denominator.
rrusczyk
2011-03-19 21:21:10
What is the numerator?
What is the numerator?
vcez
2011-03-19 21:21:35
cases 1,3,4
cases 1,3,4
v_Enhance
2011-03-19 21:21:35
F = n6 + n24 + n42
F = n6 + n24 + n42
.cpp
2011-03-19 21:21:35
n_6+n_24+n_42
n_6+n_24+n_42
vcez
2011-03-19 21:21:35
first, third, and fourth cases in the list
first, third, and fourth cases in the list
adalander
2011-03-19 21:21:35
oops 1,3,4
oops 1,3,4
carmelninja
2011-03-19 21:21:35
n_6 + n_24 + n_42
n_6 + n_24 + n_42
Kinata12
2011-03-19 21:21:38
The sum of cases 1, 3, and 4
The sum of cases 1, 3, and 4
rrusczyk
2011-03-19 21:21:40
We want to divide the cases where four men stand together by the total number of cases:
We want to divide the cases where four men stand together by the total number of cases:
rrusczyk
2011-03-19 21:21:46
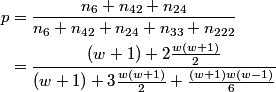
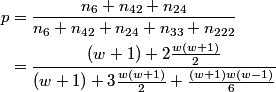
ahaanomegas
2011-03-19 21:21:59
Huge w bashing, here!
Huge w bashing, here!
BarbieRocks
2011-03-19 21:21:59
cancel w+1
cancel w+1
.cpp
2011-03-19 21:21:59
Factor out w+1.
Factor out w+1.
rrusczyk
2011-03-19 21:22:01
I'll spare you the algebra.
I'll spare you the algebra.
rrusczyk
2011-03-19 21:22:05
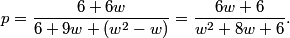
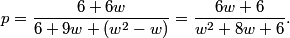
Jasmine8925
2011-03-19 21:22:09
p is less than or equal to 1/100
p is less than or equal to 1/100
rrusczyk
2011-03-19 21:22:16
More bashing.
More bashing.
rrusczyk
2011-03-19 21:22:17
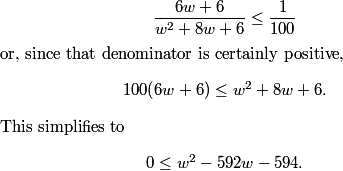
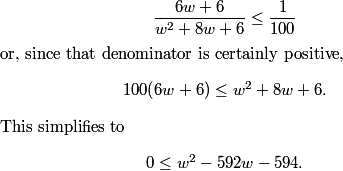
rrusczyk
2011-03-19 21:22:49
What do we want to find here?
What do we want to find here?
eb8368
2011-03-19 21:23:08
The least possible value of w
The least possible value of w
tan90
2011-03-19 21:23:08
The minimum value for w
The minimum value for w
calvinhobbesliker
2011-03-19 21:23:08
Lower bound
Lower bound
adalander
2011-03-19 21:23:08
The least number of w.
The least number of w.
Jasmine8925
2011-03-19 21:23:11
minimize w
minimize w
centrino
2011-03-19 21:23:11
smallest value of w
smallest value of w
policecap
2011-03-19 21:23:11
w minimum
w minimum
rrusczyk
2011-03-19 21:23:21
And how can we do that?
And how can we do that?
rrusczyk
2011-03-19 21:24:14
There are lots of ways to do this
There are lots of ways to do this
GoldenFrog1618
2011-03-19 21:24:28
594<=w(w-592)
594<=w(w-592)
.cpp
2011-03-19 21:24:28
Complete the square for (w-296)^2 - (296^2 + 594).
Complete the square for (w-296)^2 - (296^2 + 594).
BarbieRocks
2011-03-19 21:24:28
w(w-592)>594 so it makes sense to trie numbers near 592
w(w-592)>594 so it makes sense to trie numbers near 592
edisonchew240
2011-03-19 21:24:28
Use completing the square
Use completing the square
vcez
2011-03-19 21:24:28
find the roots
find the roots
rrusczyk
2011-03-19 21:24:50
Here's one way to do this thinking about roots:
Here's one way to do this thinking about roots:
rrusczyk
2011-03-19 21:24:51
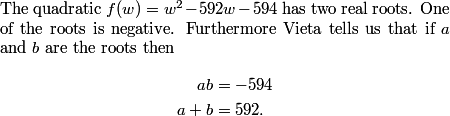
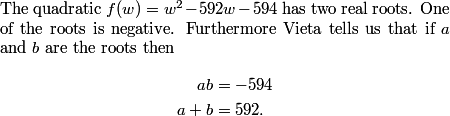
rrusczyk
2011-03-19 21:25:03
Since the numbers -594 and 592 are large and pretty close in magnitude, it looks like the negative root must be really close to -1 and the positive root has to be a little more than 592.
Since the numbers -594 and 592 are large and pretty close in magnitude, it looks like the negative root must be really close to -1 and the positive root has to be a little more than 592.
rrusczyk
2011-03-19 21:25:15
What do we find as our minimal w?
What do we find as our minimal w?
bridgemaster
2011-03-19 21:25:29
594
594
eb8368
2011-03-19 21:25:29
w=594 !
w=594 !
prezcoin
2011-03-19 21:25:29
w= 594
w= 594
DystopianStriker
2011-03-19 21:25:31
594
594
theone142857
2011-03-19 21:25:31
594
594
.cpp
2011-03-19 21:25:33
594, which is our answer.
594, which is our answer.
rrusczyk
2011-03-19 21:25:36
Let's see where the root is in relation to 593.
Let's see where the root is in relation to 593.
rrusczyk
2011-03-19 21:25:39
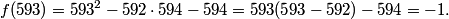
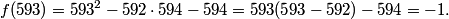
rrusczyk
2011-03-19 21:25:45
So f is still negative at 593.
So f is still negative at 593.
rrusczyk
2011-03-19 21:25:48
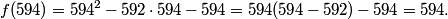
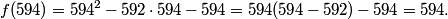
rrusczyk
2011-03-19 21:25:51
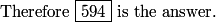
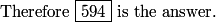
BarbieRocks
2011-03-19 21:26:05
why on earth would 6 men and 594 women stand in a line
why on earth would 6 men and 594 women stand in a line
rrusczyk
2011-03-19 21:26:19
Justin Bieber concert
Justin Bieber concert
rrusczyk
2011-03-19 21:26:35
OK, on we rollll
OK, on we rollll
.cpp
2011-03-19 21:26:48
6 = 0.01 (594+6), oddly.
6 = 0.01 (594+6), oddly.
ksun48
2011-03-19 21:26:48
also there are 600 total people. Is that significant
also there are 600 total people. Is that significant
rrusczyk
2011-03-19 21:26:59
Interesting; may want to check that out for some other numbers...
Interesting; may want to check that out for some other numbers...
rrusczyk
2011-03-19 21:27:04
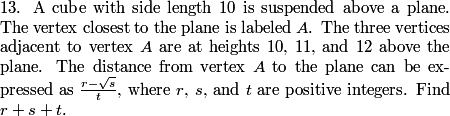
rrusczyk
2011-03-19 21:27:12
At first glance this looks icky. At second glance too.
At first glance this looks icky. At second glance too.
GoldenFrog1618
2011-03-19 21:27:40
use coordinates
use coordinates
Jasmine8925
2011-03-19 21:28:00
coordinates will still be icky
coordinates will still be icky
rrusczyk
2011-03-19 21:28:20
How can we make coordinates less icky ?
How can we make coordinates less icky ?
tan90
2011-03-19 21:28:47
If A is at the origin?
If A is at the origin?
kangchangood
2011-03-19 21:28:47
put origin at proper location..
put origin at proper location..
jeff10
2011-03-19 21:28:50
change x, y, and z axis to the side lengths
change x, y, and z axis to the side lengths
rrusczyk
2011-03-19 21:29:03
There are lots of ways to solve this problem; some are messier than others.
There are lots of ways to solve this problem; some are messier than others.
rrusczyk
2011-03-19 21:29:21
We have three important lines that are mutually perpendicular -- each perpendicular to the other two.
We have three important lines that are mutually perpendicular -- each perpendicular to the other two.
rrusczyk
2011-03-19 21:29:24
We're in space.
We're in space.
aerrowfinn72
2011-03-19 21:29:36
those are x,y,z axes
those are x,y,z axes
tan90
2011-03-19 21:29:39
Make them the axes
Make them the axes
rrusczyk
2011-03-19 21:29:44
So, we make these three lines (the edges of the cube) the axes.
So, we make these three lines (the edges of the cube) the axes.
rrusczyk
2011-03-19 21:29:51
So I would let A = (0,0,0) and let our three points P,Q,R be (10,0,0), (0,10,0), and (0,0,10). Suppose these points have distance 10, 11, 12 from some plane.
So I would let A = (0,0,0) and let our three points P,Q,R be (10,0,0), (0,10,0), and (0,0,10). Suppose these points have distance 10, 11, 12 from some plane.
rrusczyk
2011-03-19 21:29:55
What's the generic equation for a plane in 3-space?
What's the generic equation for a plane in 3-space?
.cpp
2011-03-19 21:30:27
Ax+By+Cz=D.
Ax+By+Cz=D.
karatemagic7
2011-03-19 21:30:28
ax +by+cz=d
ax +by+cz=d
NoWayHaze
2011-03-19 21:30:28
ax+by+cz+d=0
ax+by+cz+d=0
centrino
2011-03-19 21:30:28
ax+by+cz=d
ax+by+cz=d
rrusczyk
2011-03-19 21:30:35
ax + by + cz+ d = 0.
ax + by + cz+ d = 0.
rrusczyk
2011-03-19 21:30:47
And what's the distance from a point (p,q,r) to that plane?
And what's the distance from a point (p,q,r) to that plane?
AlphaMath1
2011-03-19 21:30:56
Don't tell me we have to use that formula again!
Don't tell me we have to use that formula again!
rrusczyk
2011-03-19 21:31:04
Sadly, this is the cleanest solution.
Sadly, this is the cleanest solution.
BarbieRocks
2011-03-19 21:31:48
|pa+qb+rc+d|/sqrt(a^2+b^2+c^2)
|pa+qb+rc+d|/sqrt(a^2+b^2+c^2)
karatemagic7
2011-03-19 21:31:48
(ap+bq+cr+d)/(a^2+b^2+c^2)^.5
(ap+bq+cr+d)/(a^2+b^2+c^2)^.5
gh625
2011-03-19 21:31:48
|ax+by+cz+d|/sqrt{a^2+b^2+c^2}
|ax+by+cz+d|/sqrt{a^2+b^2+c^2}
js2082
2011-03-19 21:31:48
|ax + by + cz + d|/(a*a+b*b+c*c)**0.5
|ax + by + cz + d|/(a*a+b*b+c*c)**0.5
rrusczyk
2011-03-19 21:32:03
We can think of this as "plugging" the point into the equation of the plane, and then dividing by a normalizing factor:
We can think of this as "plugging" the point into the equation of the plane, and then dividing by a normalizing factor:
.cpp
2011-03-19 21:32:05
|Ax+By+Cz+D|/sqrt(A^2+B^2+C^2)
|Ax+By+Cz+D|/sqrt(A^2+B^2+C^2)
rrusczyk
2011-03-19 21:32:09
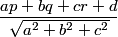
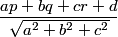
rrusczyk
2011-03-19 21:32:18
Note this is a signed distance: it's positive for all points on one side of the plane, and negative for all points on the other side.
Note this is a signed distance: it's positive for all points on one side of the plane, and negative for all points on the other side.
rrusczyk
2011-03-19 21:32:21
(We used the similar formula for the distance from a point to a line in Problem 3.)
(We used the similar formula for the distance from a point to a line in Problem 3.)
JSGandora
2011-03-19 21:32:51
there's an absolute value for the numerator right?
there's an absolute value for the numerator right?
.cpp
2011-03-19 21:33:13
It's a signed distance here.
It's a signed distance here.
JSGandora
2011-03-19 21:33:13
oh, sorry. it's a signed distance.
oh, sorry. it's a signed distance.
rrusczyk
2011-03-19 21:33:14
We're taking signed distance here --> "above the plane" is positive and "below the plane" is negative.
We're taking signed distance here --> "above the plane" is positive and "below the plane" is negative.
rrusczyk
2011-03-19 21:33:23
Now, let's look at our plane equation:
Now, let's look at our plane equation:
rrusczyk
2011-03-19 21:33:29
ax + by + cz + d = 0.
ax + by + cz + d = 0.
rrusczyk
2011-03-19 21:33:46
Can we make any assumptions here that will make that distance formula less nasty
Can we make any assumptions here that will make that distance formula less nasty
AlphaMath1
2011-03-19 21:34:02
a=1
a=1
rrusczyk
2011-03-19 21:34:14
We can scale the constants a,b,c,d by anything.
We can scale the constants a,b,c,d by anything.
rrusczyk
2011-03-19 21:34:34
What would be a really nice scaling to choose, to make the distance formula not nasty?
What would be a really nice scaling to choose, to make the distance formula not nasty?
karatemagic7
2011-03-19 21:34:40
We can assume that (a^2+b^2+c^2)=1
We can assume that (a^2+b^2+c^2)=1
rrusczyk
2011-03-19 21:34:48
We can multiply the equation of the plane by any nonzero constant we want!
We can multiply the equation of the plane by any nonzero constant we want!
rrusczyk
2011-03-19 21:35:06
So, we can scale it such that a^2 + b^2 + c^2 = 1!
So, we can scale it such that a^2 + b^2 + c^2 = 1!
Jasmine8925
2011-03-19 21:35:21
how do we know it's possible to scale it like that?
how do we know it's possible to scale it like that?
gh625
2011-03-19 21:35:40
Multiply both sides by the same number.
Multiply both sides by the same number.
rrusczyk
2011-03-19 21:35:47
Because we can multiply the equation of a plane by any constant we want to and it won't change the plane.
Because we can multiply the equation of a plane by any constant we want to and it won't change the plane.
rrusczyk
2011-03-19 21:35:51
x+y+z = 9
x+y+z = 9
rrusczyk
2011-03-19 21:35:55
is the same plane as
is the same plane as
rrusczyk
2011-03-19 21:36:00
3x+3y+3z = 27
3x+3y+3z = 27
rrusczyk
2011-03-19 21:36:02
And so on:
And so on:
GoldenFrog1618
2011-03-19 21:36:05
let a^2+b^2+c^2=e^2, divide each number by e
let a^2+b^2+c^2=e^2, divide each number by e
rrusczyk
2011-03-19 21:36:15
That sure simplifies our distance formula.
That sure simplifies our distance formula.
rrusczyk
2011-03-19 21:36:42
If we have a^2 + b^2 +c^2 =1 , we have ap+bq+cr + d as our distance formula.
If we have a^2 + b^2 +c^2 =1 , we have ap+bq+cr + d as our distance formula.
rrusczyk
2011-03-19 21:36:57
So, what equations do we get now?
So, what equations do we get now?
gh625
2011-03-19 21:37:59
10a+d=10, 10b+d=11, 10c+d=12
10a+d=10, 10b+d=11, 10c+d=12
.cpp
2011-03-19 21:37:59
10 = a(10)+d, 11 = b(10)+d, 12 = c(10)+d.
10 = a(10)+d, 11 = b(10)+d, 12 = c(10)+d.
tan90
2011-03-19 21:37:59
10a + d = 10, 10b + d = 11, 10c + d = 12
10a + d = 10, 10b + d = 11, 10c + d = 12
etude
2011-03-19 21:37:59
10a+d = 10, 10b+d = 11, 10c+d = 12.
10a+d = 10, 10b+d = 11, 10c+d = 12.
rrusczyk
2011-03-19 21:38:43
We just cram the other vertices into our new distance formula.
We just cram the other vertices into our new distance formula.
rrusczyk
2011-03-19 21:38:49
They would have looked like this:
They would have looked like this:
etude
2011-03-19 21:38:51
We have (10a + d)/sqrt(a^2+b^2+c^2) = 10, (10b + d)/sqrt(a^2+b^2+c^2) = 11, and (10c + d)/sqrt(a^2+b^2+c^2) = 12.
We have (10a + d)/sqrt(a^2+b^2+c^2) = 10, (10b + d)/sqrt(a^2+b^2+c^2) = 11, and (10c + d)/sqrt(a^2+b^2+c^2) = 12.
rrusczyk
2011-03-19 21:39:01
But we cleverly let a^2 + b^2 + c^2 = 1
But we cleverly let a^2 + b^2 + c^2 = 1
rrusczyk
2011-03-19 21:39:16
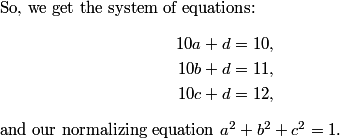
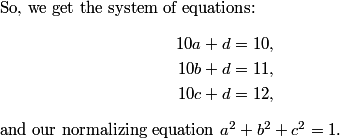
Jasmine8925
2011-03-19 21:39:25
we're trying to find d
we're trying to find d
.cpp
2011-03-19 21:39:25
Now, we just need to find d!
Now, we just need to find d!
BarbieRocks
2011-03-19 21:39:25
we need to find d
we need to find d
rrusczyk
2011-03-19 21:39:29
We want the distance from A to the plane.
We want the distance from A to the plane.
rrusczyk
2011-03-19 21:39:32
But this is just d, because A=(0,0,0) and a^2+b^2+c^2 = 1.
But this is just d, because A=(0,0,0) and a^2+b^2+c^2 = 1.
rrusczyk
2011-03-19 21:39:42
So we have to solve the above system for d.
So we have to solve the above system for d.
rrusczyk
2011-03-19 21:39:54
What's the quickest way to do this?
What's the quickest way to do this?
prezcoin
2011-03-19 21:40:27
(10-d)/10=a, (11-d)/10=b, (12-d)/10=c
(10-d)/10=a, (11-d)/10=b, (12-d)/10=c
BarbieRocks
2011-03-19 21:40:27
(10-d)^2+(11-d)^2+(12-d)^2=100
(10-d)^2+(11-d)^2+(12-d)^2=100
aerrowfinn72
2011-03-19 21:40:27
write everyhthing in terms of d
write everyhthing in terms of d
kangchangood
2011-03-19 21:40:27
100 (a^2 + b^2 + c^2) = 100
100 (a^2 + b^2 + c^2) = 100
rrusczyk
2011-03-19 21:40:46
We solve for a,b,c in terms of d in the linear equation, and plug them into the quadratic a^2+b^2+c^2 = 1.
We solve for a,b,c in terms of d in the linear equation, and plug them into the quadratic a^2+b^2+c^2 = 1.
rrusczyk
2011-03-19 21:40:49
Life is a lot simpler if we get 10a, 10b, 10c into the quadratic first. This allows us to substitute for 10a, 10b, and 10c rather than a,b,c. Since a^2+b^2+c^2 = 1, we have
Life is a lot simpler if we get 10a, 10b, 10c into the quadratic first. This allows us to substitute for 10a, 10b, and 10c rather than a,b,c. Since a^2+b^2+c^2 = 1, we have
rrusczyk
2011-03-19 21:40:55
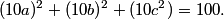
rrusczyk
2011-03-19 21:40:56
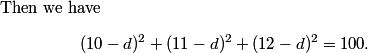
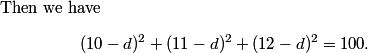
rrusczyk
2011-03-19 21:41:04
The rest is just bashing.
The rest is just bashing.
rrusczyk
2011-03-19 21:41:13
We're closing on 3 hours now, so I will bash for you.
We're closing on 3 hours now, so I will bash for you.
rrusczyk
2011-03-19 21:41:18
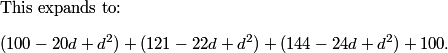
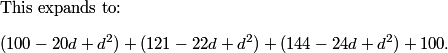
rrusczyk
2011-03-19 21:41:22
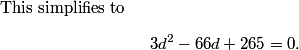
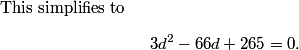
rrusczyk
2011-03-19 21:41:31
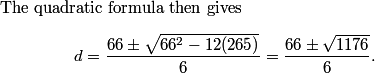
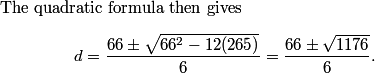
rrusczyk
2011-03-19 21:41:37
Which answer to we want, + or -?
Which answer to we want, + or -?
VIPMaster
2011-03-19 21:41:56
-
-
tan90
2011-03-19 21:41:56
-
-
ahaanomegas
2011-03-19 21:41:56
-
-
policecap
2011-03-19 21:41:56
-
-
SDLucifer
2011-03-19 21:41:56
-
-
carmelninja
2011-03-19 21:41:56
the minus
the minus
GoldenFrog1618
2011-03-19 21:41:56
- because the answer says so
- because the answer says so
gh625
2011-03-19 21:41:56
- because the answer has a - in it
- because the answer has a - in it
tan90
2011-03-19 21:41:56
the problem asked for negative
the problem asked for negative
rrusczyk
2011-03-19 21:42:09
Because the test said so, cute.
Because the test said so, cute.
rrusczyk
2011-03-19 21:42:14
Here's a better reason:
Here's a better reason:
js2082
2011-03-19 21:42:18
as it shd be less than 10
as it shd be less than 10
carmelninja
2011-03-19 21:42:18
positive value is way to big anyway
positive value is way to big anyway
rrusczyk
2011-03-19 21:42:22
Given the form of the answer required in the problem, we clearly had better have -. Indeed, A has to be closer to the plane than P,Q,R, so we need an answer between 0 and 10.
Given the form of the answer required in the problem, we clearly had better have -. Indeed, A has to be closer to the plane than P,Q,R, so we need an answer between 0 and 10.
rrusczyk
2011-03-19 21:42:26
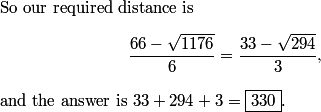
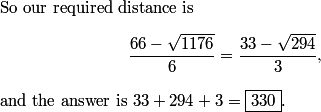
rrusczyk
2011-03-19 21:42:48
You can think later about what the other sign gives you (what significance does that other root have?)
You can think later about what the other sign gives you (what significance does that other root have?)
rrusczyk
2011-03-19 21:42:53
OK, 2 more problems.
OK, 2 more problems.
rrusczyk
2011-03-19 21:42:58
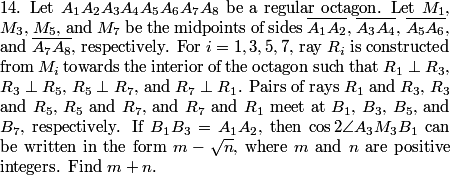
rrusczyk
2011-03-19 21:43:10
alanzee
2011-03-19 21:43:30
square!
square!
carmelninja
2011-03-19 21:43:30
a crooked square
a crooked square
VIPMaster
2011-03-19 21:43:30
a square!!!
a square!!!
calvinhobbesliker
2011-03-19 21:43:30
Square
Square
professordad
2011-03-19 21:43:30
we will have a square that's lopsided
we will have a square that's lopsided
rrusczyk
2011-03-19 21:43:33
From the symmetry of the problem, the quadrilateral formed by the B_i is a square.
From the symmetry of the problem, the quadrilateral formed by the B_i is a square.
rrusczyk
2011-03-19 21:43:37
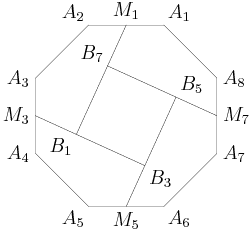

rrusczyk
2011-03-19 21:43:44
OK, now what? Can we at least simplify what we're looking for?
OK, now what? Can we at least simplify what we're looking for?
Jasmine8925
2011-03-19 21:44:09
double angle cosine formula
double angle cosine formula
rrusczyk
2011-03-19 21:44:14
Cosine of double an angle is kind of a pain. We can use the double-angle identity to give:
Cosine of double an angle is kind of a pain. We can use the double-angle identity to give:
rrusczyk
2011-03-19 21:44:20
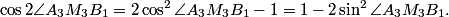
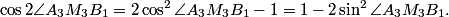
rrusczyk
2011-03-19 21:44:24
That's a nicer target. That's still a not-very-fun angle to work with, but is part of that angle easy?
That's a nicer target. That's still a not-very-fun angle to work with, but is part of that angle easy?
etude
2011-03-19 21:44:54
Draw M3M1. Then A3M3M1 is just 45 degrees.
Draw M3M1. Then A3M3M1 is just 45 degrees.
rrusczyk
2011-03-19 21:45:01
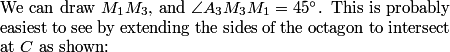
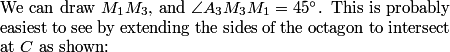
rrusczyk
2011-03-19 21:45:04
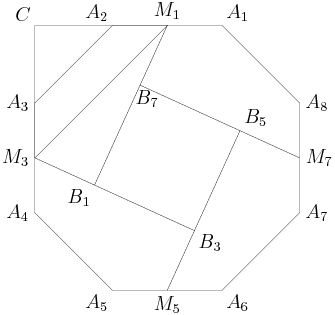

rrusczyk
2011-03-19 21:45:18
tan90
2011-03-19 21:45:42
right triangle trig
right triangle trig
etude
2011-03-19 21:45:44
Find two sides of the right triangle.
Find two sides of the right triangle.
rrusczyk
2011-03-19 21:45:47
We want sine and/or cosine of this angle, so let's label some sides.
We want sine and/or cosine of this angle, so let's label some sides.
professordad
2011-03-19 21:46:09
let M3B1 = x. Then B1M1 = 1 + x
let M3B1 = x. Then B1M1 = 1 + x
rrusczyk
2011-03-19 21:46:20
I'm going to let the sides of the square be 2.
I'm going to let the sides of the square be 2.
rrusczyk
2011-03-19 21:46:21
Why?
Why?
.cpp
2011-03-19 21:46:37
To avoid fractions.
To avoid fractions.
etude
2011-03-19 21:46:44
That eliminates fractions.
That eliminates fractions.
ParallelProcess
2011-03-19 21:46:44
midpoint divides into 1 and 1
midpoint divides into 1 and 1
ahaanomegas
2011-03-19 21:46:44
Because then we won't have fractions
Because then we won't have fractions
rrusczyk
2011-03-19 21:46:46
We can choose the scale of the octagon, so we let the side length of the octagon be 2 (if we choose 1, we get fractions, ick). We also know that B_1M_3 = B_7M_1, so we let those lengths be x:
We can choose the scale of the octagon, so we let the side length of the octagon be 2 (if we choose 1, we get fractions, ick). We also know that B_1M_3 = B_7M_1, so we let those lengths be x:
rrusczyk
2011-03-19 21:46:50
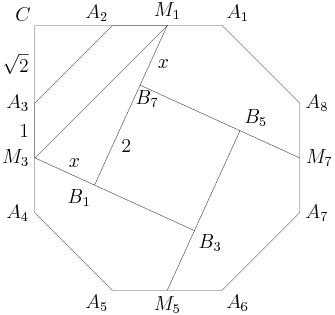

rrusczyk
2011-03-19 21:46:57
Now it is awfully tempting to pull out our hammer and bash, bash, bash.
Now it is awfully tempting to pull out our hammer and bash, bash, bash.
rrusczyk
2011-03-19 21:47:04
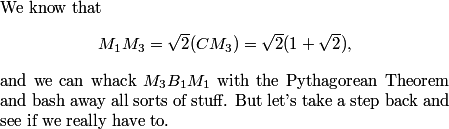
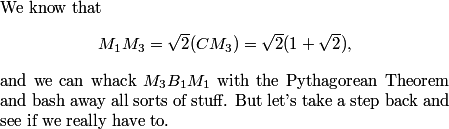
jeff10
2011-03-19 21:47:14
i think we should go for cosine
i think we should go for cosine
rrusczyk
2011-03-19 21:48:05
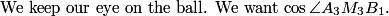
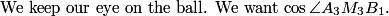
rrusczyk
2011-03-19 21:48:13
And we broke that up:
And we broke that up:
rrusczyk
2011-03-19 21:48:31
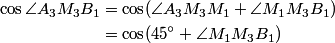
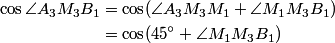
jeff10
2011-03-19 21:48:33
which is 45 + unknown angle
which is 45 + unknown angle
rrusczyk
2011-03-19 21:48:40
And what do we do with this?
And what do we do with this?
kangchangood
2011-03-19 21:48:51
identity?..
identity?..
DavidTong
2011-03-19 21:48:51
sum formula
sum formula
ahaanomegas
2011-03-19 21:48:54
Sum of angle formula
Sum of angle formula
etude
2011-03-19 21:48:54
Use cosine addition angle identity.
Use cosine addition angle identity.
rrusczyk
2011-03-19 21:48:58
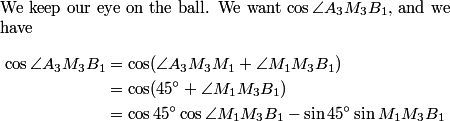
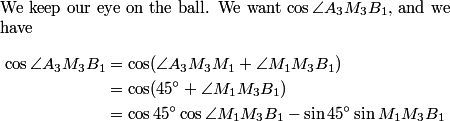
rrusczyk
2011-03-19 21:49:03
Keep on rolling...
Keep on rolling...
kangchangood
2011-03-19 21:49:13
pull out 45 thing.
pull out 45 thing.
rrusczyk
2011-03-19 21:49:17
Keep going...
Keep going...
carmelninja
2011-03-19 21:49:21
and the x terms should cancel out
and the x terms should cancel out
rrusczyk
2011-03-19 21:49:25
Do they?
Do they?
GoldenFrog1618
2011-03-19 21:50:30
yes!
yes!
VIPMaster
2011-03-19 21:50:30
Yes, they do - we're left with 2/hypotenuse
Yes, they do - we're left with 2/hypotenuse
etude
2011-03-19 21:50:30
sqrt(2)/2 [x/c + 2-x/c] = sqrt(2)/2 *2/c, where c is M3M1.
sqrt(2)/2 [x/c + 2-x/c] = sqrt(2)/2 *2/c, where c is M3M1.
professordad
2011-03-19 21:50:30
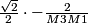
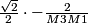
rrusczyk
2011-03-19 21:50:46
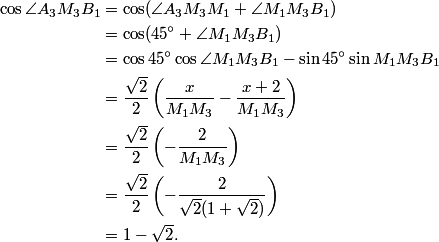
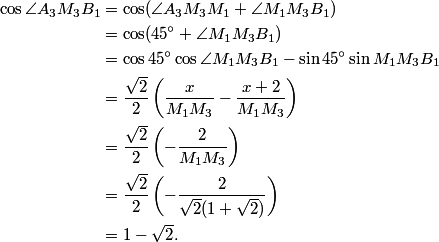
rrusczyk
2011-03-19 21:50:51
Booyah! Touchdown! We make miracles happen!
Booyah! Touchdown! We make miracles happen!
jeff10
2011-03-19 21:51:06
negative number?
negative number?
rrusczyk
2011-03-19 21:51:13
Yes, the angle was obtuse
Yes, the angle was obtuse
rrusczyk
2011-03-19 21:51:31
Now, how do we finish?
Now, how do we finish?
carmelninja
2011-03-19 21:51:54
now find double angle
now find double angle
sindennisz
2011-03-19 21:51:54
square it?
square it?
dlennon
2011-03-19 21:51:54
Now find cos2<A3M3B1
Now find cos2<A3M3B1
calvinhobbesliker
2011-03-19 21:51:54
Double angle formula
Double angle formula
VIPMaster
2011-03-19 21:51:56
plug everything back into our original cosine double angle formula equation
plug everything back into our original cosine double angle formula equation
rrusczyk
2011-03-19 21:52:11
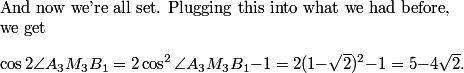
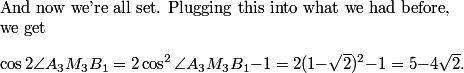
rrusczyk
2011-03-19 21:52:23


eb8368
2011-03-19 21:52:37
5-Root 32 5+32 = 37
5-Root 32 5+32 = 37
ahaanomegas
2011-03-19 21:52:37
037 is what you would bubble in
037 is what you would bubble in
GoldenFrog1618
2011-03-19 21:52:45
last one!
last one!
rrusczyk
2011-03-19 21:52:47
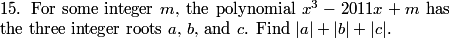
rrusczyk
2011-03-19 21:52:56
There are a ton of ways to do this one...
There are a ton of ways to do this one...
eb8368
2011-03-19 21:52:58
Vieta's + Bash !
Vieta's + Bash !
mhy123
2011-03-19 21:53:00
Vieta's bash
Vieta's bash
rrusczyk
2011-03-19 21:53:07
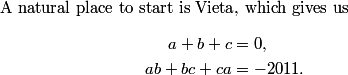
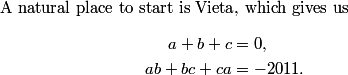
rrusczyk
2011-03-19 21:53:14
Before we start substituting and cranking through algebra, does a quick glance at these equations tell you anything about a,b,c?
Before we start substituting and cranking through algebra, does a quick glance at these equations tell you anything about a,b,c?
BarbieRocks
2011-03-19 21:53:38
one even, 2 odd
one even, 2 odd
carmelninja
2011-03-19 21:53:38
two are odd, one is even
two are odd, one is even
rrusczyk
2011-03-19 21:53:44
The first equation tells us that either all three of a,b,c are even, or one is even and the other two odd. The second equation tells us that we cannot have all three even. So, we know that one is even and the other two are odd.
The first equation tells us that either all three of a,b,c are even, or one is even and the other two odd. The second equation tells us that we cannot have all three even. So, we know that one is even and the other two are odd.
rrusczyk
2011-03-19 21:53:48
We might substitute c = 2k at this point, but let's hold off on that, so as not to ruin our nice symmetry yet.
We might substitute c = 2k at this point, but let's hold off on that, so as not to ruin our nice symmetry yet.
AlphaMath1
2011-03-19 21:53:55
a=-b-c
a=-b-c
professordad
2011-03-19 21:53:55
a+b=-c
a+b=-c
BarbieRocks
2011-03-19 21:53:55
plug in c=-a-b and get a^2+ab+b^2=2011
plug in c=-a-b and get a^2+ab+b^2=2011
rrusczyk
2011-03-19 21:54:06
About the only thing left to do is substitute, so we let a=-b-c in the second equation.
About the only thing left to do is substitute, so we let a=-b-c in the second equation.
rrusczyk
2011-03-19 21:54:12
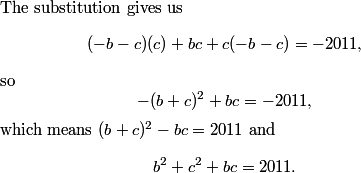
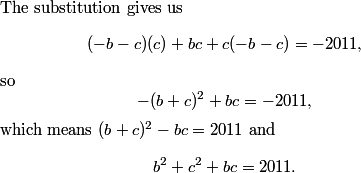
rrusczyk
2011-03-19 21:54:16
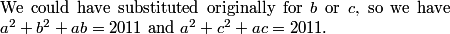
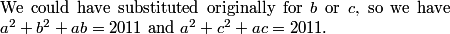
rrusczyk
2011-03-19 21:54:32
(I'm going quickly through this because I think a lot of you probably got that far that fast on the test.)
(I'm going quickly through this because I think a lot of you probably got that far that fast on the test.)
rrusczyk
2011-03-19 21:54:49
Now, you might just start guessing here, and you might get there pretty quick.
Now, you might just start guessing here, and you might get there pretty quick.
rrusczyk
2011-03-19 21:54:57
I'm going to talk a bit about how to narrow the search.
I'm going to talk a bit about how to narrow the search.
rrusczyk
2011-03-19 21:55:00
What kind of equation is each of these?
What kind of equation is each of these?
anonymous0
2011-03-19 21:55:12
quadratic
quadratic
VIPMaster
2011-03-19 21:55:12
quadratic-ish
quadratic-ish
prezcoin
2011-03-19 21:55:12
quadratic in a
quadratic in a
adalander
2011-03-19 21:55:14
Quadratic.
Quadratic.
rrusczyk
2011-03-19 21:55:17
These are quadratics.
These are quadratics.
rrusczyk
2011-03-19 21:55:23
What can we do with quadratics?
What can we do with quadratics?
professordad
2011-03-19 21:55:34
quadratic formula
quadratic formula
gh625
2011-03-19 21:55:34
use the quadratic formula
use the quadratic formula
bulutcocuk
2011-03-19 21:55:34
quadratic formula!
quadratic formula!
tan90
2011-03-19 21:55:34
quadratic formula!
quadratic formula!
VIPMaster
2011-03-19 21:55:36
quadratic formula
quadratic formula
rrusczyk
2011-03-19 21:56:01
This can be a particularly useful tool in quadratic Diophantine equations (equations we must solve in integers)
This can be a particularly useful tool in quadratic Diophantine equations (equations we must solve in integers)
bojobo
2011-03-19 21:56:13
we express one value in terms of the other
we express one value in terms of the other
rrusczyk
2011-03-19 21:56:17
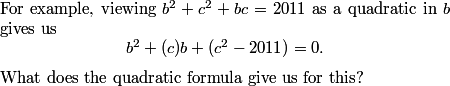
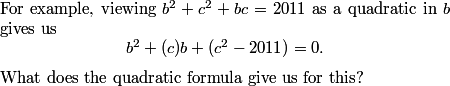
karatemagic7
2011-03-19 21:57:06
4*2011-3c^2 is a square.
4*2011-3c^2 is a square.
.cpp
2011-03-19 21:57:07
(-c+-sqrt(c^2+8044-c^2))/2 = root.
(-c+-sqrt(c^2+8044-c^2))/2 = root.
calvinhobbesliker
2011-03-19 21:57:07
-c+-sqrt(c^2-4(c^2-2011))/2
-c+-sqrt(c^2-4(c^2-2011))/2
gh625
2011-03-19 21:57:07
b=(-c+/-sqrt{-3c^2+8044})/2
b=(-c+/-sqrt{-3c^2+8044})/2
rrusczyk
2011-03-19 21:57:09
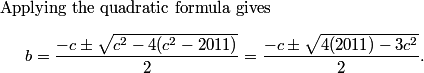
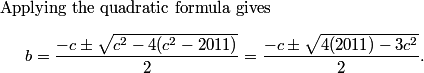
JSGandora
2011-03-19 21:57:14
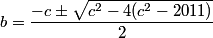
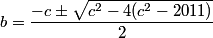
rrusczyk
2011-03-19 21:57:17
We could start cranking through trial-and-error to find a value of c that makes the discriminant a perfect square, but how can we make life a little easier?
We could start cranking through trial-and-error to find a value of c that makes the discriminant a perfect square, but how can we make life a little easier?
GoldenFrog1618
2011-03-19 21:57:38
assume c is even
assume c is even
calvinhobbesliker
2011-03-19 21:57:38
C is even
C is even
VIPMaster
2011-03-19 21:57:38
c is even
c is even
karatemagic7
2011-03-19 21:57:39
Assume c is the even one
Assume c is the even one
rrusczyk
2011-03-19 21:57:42
We remember that one of a,b,c is even, and that if we choose c to be the even one, that will simplify the radical.
We remember that one of a,b,c is even, and that if we choose c to be the even one, that will simplify the radical.
rrusczyk
2011-03-19 21:57:48
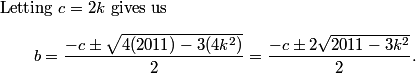
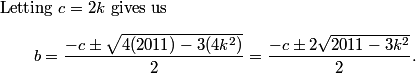
rrusczyk
2011-03-19 21:58:04
Now life is a lot easier. Can we make life even easier before we start guessing k's?
Now life is a lot easier. Can we make life even easier before we start guessing k's?
rrusczyk
2011-03-19 21:58:41
I'm trying to narrow how much I have to guess. What mod is good for squares?
I'm trying to narrow how much I have to guess. What mod is good for squares?
panjia123
2011-03-19 21:59:01
4
4
etude
2011-03-19 21:59:01
mod 4
mod 4
BarbieRocks
2011-03-19 21:59:01
4
4
calvinhobbesliker
2011-03-19 21:59:01
4
4
vcez
2011-03-19 21:59:01
4
4
Jasmine8925
2011-03-19 21:59:01
4?
4?
superrook
2011-03-19 21:59:01
4
4
NoWayHaze
2011-03-19 21:59:01
4
4
munygrubber
2011-03-19 21:59:01
4
4
JSGandora
2011-03-19 21:59:01
4
4
vcez
2011-03-19 21:59:01
mod 4
mod 4
Kinata12
2011-03-19 21:59:01
mod 4
mod 4
rrusczyk
2011-03-19 21:59:03
Squares must be 0 or 1 mod 4.
Squares must be 0 or 1 mod 4.
rrusczyk
2011-03-19 21:59:15
What do we know immediately about k, then?
What do we know immediately about k, then?
karatemagic7
2011-03-19 21:59:39
k has to be odd in order for the discrimant to be 0 or 1 (mod 4)
k has to be odd in order for the discrimant to be 0 or 1 (mod 4)
fractals
2011-03-19 21:59:40
must be odd
must be odd
VIPMaster
2011-03-19 21:59:40
its odd!
its odd!
rrusczyk
2011-03-19 21:59:43
We notice that because 2011 is 3 mod 4, and no square is congruent to 3 mod 4, we cannot have k be even.
We notice that because 2011 is 3 mod 4, and no square is congruent to 3 mod 4, we cannot have k be even.
rrusczyk
2011-03-19 21:59:49
So, now we really have narrowed our search. We want 2011-3k^2 to be a perfect square, and we know that k is odd. Can we narrow it even more at a glance?
So, now we really have narrowed our search. We want 2011-3k^2 to be a perfect square, and we know that k is odd. Can we narrow it even more at a glance?
.cpp
2011-03-19 22:00:10
k has to be pretty small.
k has to be pretty small.
rrusczyk
2011-03-19 22:00:11
(I'm really just teaching you tricks of the trade here; we've already narrowed the search a lot.)
(I'm really just teaching you tricks of the trade here; we've already narrowed the search a lot.)
panjia123
2011-03-19 22:00:16
lower than 26
lower than 26
rrusczyk
2011-03-19 22:00:36
So, we don't have many to test. We can just start going up through the odds.
So, we don't have many to test. We can just start going up through the odds.
rrusczyk
2011-03-19 22:00:44
We also know that k cannot end in 1 or 9, since either of these would have 2011-3k^2 ending in 8, and no square ends in 8.
We also know that k cannot end in 1 or 9, since either of these would have 2011-3k^2 ending in 8, and no square ends in 8.
rrusczyk
2011-03-19 22:00:47
All right, now we only have a small handful of options to check: odd numbers ending in 3,5, or 7, and we know k can't be 25 or larger, since 2011-3k^2 would then be negative.
All right, now we only have a small handful of options to check: odd numbers ending in 3,5, or 7, and we know k can't be 25 or larger, since 2011-3k^2 would then be negative.
eb8368
2011-03-19 22:00:59
k = 5 works
k = 5 works
SDLucifer
2011-03-19 22:00:59
k=5
k=5
.cpp
2011-03-19 22:01:03
k = 5 works.
k = 5 works.
jeff10
2011-03-19 22:01:03
k=5
k=5
rrusczyk
2011-03-19 22:01:05
We start from the beginning, and see that 2011 - 3(5^2) = 1936 = 44^2. Success!
We start from the beginning, and see that 2011 - 3(5^2) = 1936 = 44^2. Success!
rrusczyk
2011-03-19 22:01:16
And how do we finish?
And how do we finish?
fractals
2011-03-19 22:02:09
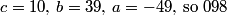
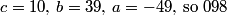
kangchangood
2011-03-19 22:02:09
from c= 10 just plug that in the other equations and get value of a and b
from c= 10 just plug that in the other equations and get value of a and b
eb8368
2011-03-19 22:02:12
Find c , and plug it back into the original equation
Find c , and plug it back into the original equation
calvinhobbesliker
2011-03-19 22:02:12
c is thus 10
c is thus 10
gh625
2011-03-19 22:02:14
c=10, then solve for a and b
c=10, then solve for a and b
kangchangood
2011-03-19 22:02:18
plug and get the values
plug and get the values
AlphaMath1
2011-03-19 22:02:20
c=2k=10
c=2k=10
karatemagic7
2011-03-19 22:02:20
c=10, so b=39, so a=-49, so the sum of the abs. is 98.
c=10, so b=39, so a=-49, so the sum of the abs. is 98.
.cpp
2011-03-19 22:02:22
Then, |a| + |b| + |c| = 39+49+10 = 098.
Then, |a| + |b| + |c| = 39+49+10 = 098.
etude
2011-03-19 22:02:24
c = 10, b = 39, a = -49 by plug-and-chug. Thus 098.
c = 10, b = 39, a = -49 by plug-and-chug. Thus 098.
rrusczyk
2011-03-19 22:02:31
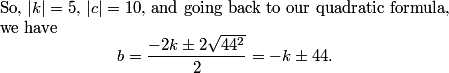
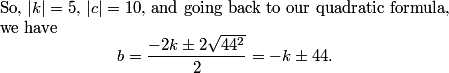
rrusczyk
2011-03-19 22:02:36
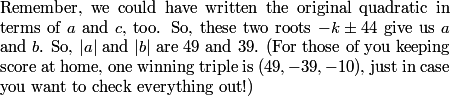
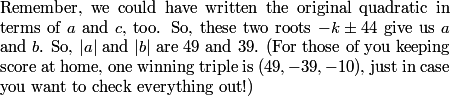
policecap
2011-03-19 22:02:49
98
98
eb8368
2011-03-19 22:02:49
098
098
ahaanomegas
2011-03-19 22:02:49
098 = Answer
098 = Answer
danielguo94
2011-03-19 22:02:49
$ 098 $
$ 098 $
DystopianStriker
2011-03-19 22:02:49
ans is 098
ans is 098
rrusczyk
2011-03-19 22:03:03
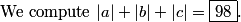
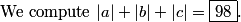
calculatorwiz
2011-03-19 22:03:05
and that's how u ace an aime in 3 hours
and that's how u ace an aime in 3 hours
rrusczyk
2011-03-19 22:03:12
Yay, we made it at the wire!!!
Yay, we made it at the wire!!!
danielguo94
2011-03-19 22:03:16
WOOT
WOOT
ahaanomegas
2011-03-19 22:03:27
WOOT!
WOOT!
Lemon123
2011-03-19 22:03:27
break included
break included
eb8368
2011-03-19 22:03:27
YAY!
YAY!
GoldenFrog1618
2011-03-19 22:03:27
thanks!
thanks!
edisonchew240
2011-03-19 22:03:27
Woot
Woot
mathelete
2011-03-19 22:03:38
wow...that really was perfect timing
wow...that really was perfect timing
GoldenFrog1618
2011-03-19 22:03:39
any other solutions to 15?
any other solutions to 15?
calculusinmath
2011-03-19 22:03:39
Thank you
Thank you
jeff10
2011-03-19 22:03:39
thank you Mr. Rusczyk
thank you Mr. Rusczyk
professordad
2011-03-19 22:03:39
wow
wow
JSGandora
2011-03-19 22:03:39
Thank you so much! :)
Thank you so much! :)
KeepingItReal
2011-03-19 22:03:39
Dang, that was amazing rrusczyk!
Dang, that was amazing rrusczyk!
bojobo
2011-03-19 22:03:39
thank you
thank you
.cpp
2011-03-19 22:03:39
Thank you very much, Mr. Rusczyk!
Thank you very much, Mr. Rusczyk!
DystopianStriker
2011-03-19 22:03:39
ty very much
ty very much
AlphaMath1
2011-03-19 22:03:39
Are all the solutions on here similar to the official ones?
Are all the solutions on here similar to the official ones?
sincostanseccsccot
2011-03-19 22:03:39
thx
thx
Lemon123
2011-03-19 22:03:39
thanks!
thanks!
rrusczyk
2011-03-19 22:03:58
Best of luck to all of you who made the USA(J)MO, and good luck to those of you who are taking the AIME II
Best of luck to all of you who made the USA(J)MO, and good luck to those of you who are taking the AIME II
jsperling
2011-03-19 22:04:07
W00t
W00t
bojobo
2011-03-19 22:04:07
hope the next is easier
hope the next is easier
kelwenp123
2011-03-19 22:04:07
thanks!
thanks!
jsperling
2011-03-19 22:04:07
Thank you Richard!
Thank you Richard!
hrithikguy
2011-03-19 22:04:07
hi
hi
rasgorial
2011-03-19 22:04:07
THANK YOU!
THANK YOU!
hrithikguy
2011-03-19 22:04:07
HI
HI
sindennisz
2011-03-19 22:04:07
Thank you Mr. Rusczyk
Thank you Mr. Rusczyk
hrithikguy
2011-03-19 22:04:07
THANKS
THANKS
carmelninja
2011-03-19 22:04:07
thanks
thanks
jellymoop
2011-03-19 22:04:07
That was heartbreakingly beautiful....
That was heartbreakingly beautiful....
dlennon
2011-03-19 22:04:07
Thanks!:bow:
Thanks!:bow:
panjia123
2011-03-19 22:04:07
thanks
thanks
eb8368
2011-03-19 22:04:07
Thanks!
Thanks!
centralbs
2011-03-19 22:04:07
Thanks!!!
Thanks!!!
hrithikguy
2011-03-19 22:04:07
Thank yoU!!
Thank yoU!!
pi.guy3.14
2011-03-19 22:04:07
thank you!!!
thank you!!!
gh625
2011-03-19 22:04:07
thank you
thank you
SDLucifer
2011-03-19 22:04:07
thank you!
thank you!
chessmaster7
2011-03-19 22:04:07
thank you
thank you
apple.singer
2011-03-19 22:04:07
nice job guys
nice job guys
rdj5933mile5
2011-03-19 22:04:07
Thank you
Thank you
anonymous0
2011-03-19 22:04:07
thanks you very much, sir!
thanks you very much, sir!
rasgorial
2011-03-19 22:04:07
thank you thank you thank you
thank you thank you thank you
girishvar12
2011-03-19 22:04:07
thanks
thanks
sincostanseccsccot
2011-03-19 22:04:07
bye
bye
edisonchew240
2011-03-19 22:04:07
Thanks man!
Thanks man!
professordad
2011-03-19 22:04:07
THANK YOU :bow:
THANK YOU :bow:
policecap
2011-03-19 22:04:07
ttocs
ttocs
apple.singer
2011-03-19 22:04:07
and thanks Mr. Ruscyzk
and thanks Mr. Ruscyzk
BarbieRocks
2011-03-19 22:04:12
im scared these problems end ened up asier than i thought--its just the order--now idk what the index is
im scared these problems end ened up asier than i thought--its just the order--now idk what the index is
rrusczyk
2011-03-19 22:04:24
Nah -- they only look easy because there are 200 of us working on them!
Nah -- they only look easy because there are 200 of us working on them!
VIPMaster
2011-03-19 22:04:35
Thank you so much for your time Mr. Rusczyk. As always, ArtOfProblemSolving is my first source for everything math-related!
Thank you so much for your time Mr. Rusczyk. As always, ArtOfProblemSolving is my first source for everything math-related!
hrithikguy
2011-03-19 22:04:36
hi
hi
Jasmine8925
2011-03-19 22:04:36
thank you!
thank you!
inquisitivity
2011-03-19 22:04:36
Thank you!
Thank you!
july5117
2011-03-19 22:04:36
wow
wow
ahaanomegas
2011-03-19 22:04:36
Thank you for the class, Mr. Rusczyk!
Thank you for the class, Mr. Rusczyk!
calculusinmath
2011-03-19 22:05:14
I look forward to reading your book.
I look forward to reading your book.
rrusczyk
2011-03-19 22:05:21
I look forward to your reading my book :)
I look forward to your reading my book :)
KeepingItReal
2011-03-19 22:05:24
This is my first time at one of these classes, does AOPS have many of these sessions?
This is my first time at one of these classes, does AOPS have many of these sessions?
rrusczyk
2011-03-19 22:05:33
We do all the AMC and AIME tests like this.
We do all the AMC and AIME tests like this.
GoldenFrog1618
2011-03-19 22:05:35
Wow! you were able to attract 200 people to do math on a Saturday for 3 hours.
Wow! you were able to attract 200 people to do math on a Saturday for 3 hours.
rrusczyk
2011-03-19 22:06:03
Yep. If I could, I think I would invest in the futures of these 200 people over any other group of 200 people you might get online at one time.
Yep. If I could, I think I would invest in the futures of these 200 people over any other group of 200 people you might get online at one time.
AlphaMath1
2011-03-19 22:06:15
Are there any plans for USA(J)MO math jams?
Are there any plans for USA(J)MO math jams?
rrusczyk
2011-03-19 22:06:39
We probably won't do that, in part because these things take forever to put together, and in part because the AMC publishes solutions the day after the test.
We probably won't do that, in part because these things take forever to put together, and in part because the AMC publishes solutions the day after the test.
iamthygod!!!!!!
2011-03-19 22:06:42
My math teacher already ordered me copies of all your books a long time ago! :bow: They are all amazing!
My math teacher already ordered me copies of all your books a long time ago! :bow: They are all amazing!
rrusczyk
2011-03-19 22:06:48
You have a good teacher :)
You have a good teacher :)
rrusczyk
2011-03-19 22:07:26
All right, it's been three hours! Thanks for coming. The transcript will be up shortly, and the room will close in a minute. It's time for dinner out here in California. Math is hungry work!
All right, it's been three hours! Thanks for coming. The transcript will be up shortly, and the room will close in a minute. It's time for dinner out here in California. Math is hungry work!
rrusczyk
2011-03-19 22:08:35
There's the schedule for future Math Jams.
There's the schedule for future Math Jams.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









