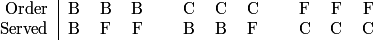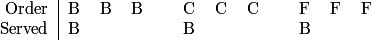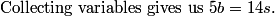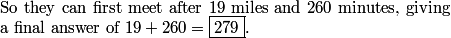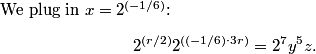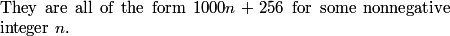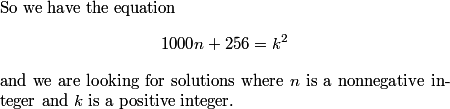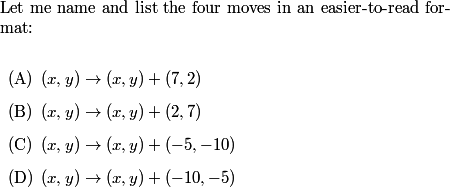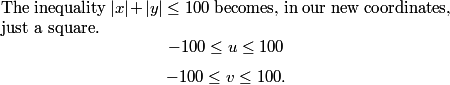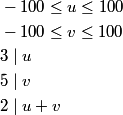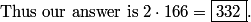2012 AIME I Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2012 AIME I.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2012-03-17 19:00:17
Welcome to the 2012 AIME I Math Jam!
Welcome to the 2012 AIME I Math Jam!
DPatrick
2012-03-17 19:00:22
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2012-03-17 19:00:30
Before we get started I would like to take a brief moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a brief moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2012-03-17 19:00:37
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
DPatrick
2012-03-17 19:00:46
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2012-03-17 19:00:57
As usual for our Math Jams, there are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
As usual for our Math Jams, there are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2012-03-17 19:01:11
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
DPatrick
2012-03-17 19:01:25
We do have two teaching assistants with us tonight to help answer your questions: Carl Lian (CatalystOfNostalgia) and David Wise (MathWise).
We do have two teaching assistants with us tonight to help answer your questions: Carl Lian (CatalystOfNostalgia) and David Wise (MathWise).
DPatrick
2012-03-17 19:01:37
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
ksun48
2012-03-17 19:01:57
Are we doing #15?
Are we doing #15?
strategist
2012-03-17 19:01:57
Are we going to go through all 15 questions?
Are we going to go through all 15 questions?
DPatrick
2012-03-17 19:02:04
Yes, we're going to do all 15 problems, in orer.
Yes, we're going to do all 15 problems, in orer.
DPatrick
2012-03-17 19:02:05
...order.
...order.
DPatrick
2012-03-17 19:02:13
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
DPatrick
2012-03-17 19:02:42
Again, if you have any questions, feel free to ask. One of our assistants will try to help you as soon as they can.
Again, if you have any questions, feel free to ask. One of our assistants will try to help you as soon as they can.
DPatrick
2012-03-17 19:02:47
With that, let's get started!
With that, let's get started!
DPatrick
2012-03-17 19:03:02
(Note that I'll always put the current problem statement up at the top of the window. You can resize the region at the top of the window by dragging the gray horizontal bar.)
(Note that I'll always put the current problem statement up at the top of the window. You can resize the region at the top of the window by dragging the gray horizontal bar.)
EricMathPath09
2012-03-17 19:03:19
Use the law of divisibility by 4.
Use the law of divisibility by 4.
DPatrick
2012-03-17 19:03:25
Right. How we can tell if a 3-digit number is a multiple of 4?
Right. How we can tell if a 3-digit number is a multiple of 4?
aopsmomisawesome
2012-03-17 19:03:39
ignore the first digit
ignore the first digit
FalconPower
2012-03-17 19:03:40
last two digits divisble by 4
last two digits divisble by 4
fireonice
2012-03-17 19:03:40
if the last two digits are divisible by 4
if the last two digits are divisible by 4
binmu
2012-03-17 19:03:40
last two digits divisible by 4
last two digits divisible by 4
strategist
2012-03-17 19:03:44
two cases: b is odd or b is even
two cases: b is odd or b is even
strategist
2012-03-17 19:03:44
cases where b is odd, b is even
cases where b is odd, b is even
DPatrick
2012-03-17 19:04:06
We only need to look at the last two digits. And it's possible to divide this in the cases where b is even and where b is odd.
We only need to look at the last two digits. And it's possible to divide this in the cases where b is even and where b is odd.
19oshawott98
2012-03-17 19:04:19
b odd=a/c being 2 or 6
b odd=a/c being 2 or 6
Iggy Iguana
2012-03-17 19:04:29
if b even: 4 and 8
if b even: 4 and 8
aopsmomisawesome
2012-03-17 19:04:35
If b is odd, we can last digithave 2 or 6; if b is even, our last digit can be 4 or 8 (no zero)
If b is odd, we can last digithave 2 or 6; if b is even, our last digit can be 4 or 8 (no zero)
DPatrick
2012-03-17 19:04:46
Yes. The last two digits must be e0, e4, e8, o2, or o6, where "e" is any even digit and "o" is any odd digit.
Yes. The last two digits must be e0, e4, e8, o2, or o6, where "e" is any even digit and "o" is any odd digit.
DPatrick
2012-03-17 19:04:51
But we can throw away e0, because we can't have the last digit be 0.
But we can throw away e0, because we can't have the last digit be 0.
DPatrick
2012-03-17 19:04:57
So the possibilities are e4, e8, o2, and o6.
So the possibilities are e4, e8, o2, and o6.
Relativity1618
2012-03-17 19:05:23
for each be there are 2 possible values of a and c
for each be there are 2 possible values of a and c
Iggy Iguana
2012-03-17 19:05:23
so there are 2 choices for each
so there are 2 choices for each
thecmd999
2012-03-17 19:05:23
so for every b, there are 2*2=4 different a and c; since there are 10 possible b's, the answer is 4*10=40
so for every b, there are 2*2=4 different a and c; since there are 10 possible b's, the answer is 4*10=40
DPatrick
2012-03-17 19:05:32
For any possible middle digit b, there are 2 choices for a and 2 choices for c that work. (If b is even, 4 and 8 work; if b is odd, 2 and 6 work.)
For any possible middle digit b, there are 2 choices for a and 2 choices for c that work. (If b is even, 4 and 8 work; if b is odd, 2 and 6 work.)
DPatrick
2012-03-17 19:05:44
So, for each of the 10 choices of middle digit b, we have 2 choices for a and 2 choices for c.
So, for each of the 10 choices of middle digit b, we have 2 choices for a and 2 choices for c.
strategist
2012-03-17 19:05:52
then there are 2 * 2 * 10
then there are 2 * 2 * 10
Relativity1618
2012-03-17 19:06:01
2*2*10=40
2*2*10=40
va2010
2012-03-17 19:06:01
so 2*2*10=40
so 2*2*10=40
googol.plex
2012-03-17 19:06:22
Do you have to put it with the 0 in front?
Do you have to put it with the 0 in front?
eccfcco15
2012-03-17 19:06:22
why 040 instead of 40
why 040 instead of 40
DPatrick
2012-03-17 19:06:40
I put that to get you in the habit of not forgetting to bubble in the first 0 (on the AIME answer form when you're taking the contest)!
I put that to get you in the habit of not forgetting to bubble in the first 0 (on the AIME answer form when you're taking the contest)!
strategist
2012-03-17 19:07:18
836 - 715 = 121
836 - 715 = 121
19oshawott98
2012-03-17 19:07:18
836-715
836-715
leecchh
2012-03-17 19:07:20
The toal increase is 836-715=121
The toal increase is 836-715=121
DPatrick
2012-03-17 19:07:28
Right. We see that the new sequence's sum is 836 - 715 = 121 greater.
Right. We see that the new sequence's sum is 836 - 715 = 121 greater.
DPatrick
2012-03-17 19:07:37
On the other hand, we get to the new sequence by adding 1, 3, 5, etc.
On the other hand, we get to the new sequence by adding 1, 3, 5, etc.
ABCDE
2012-03-17 19:07:55
The sum of the first k odd numbers is k^2
The sum of the first k odd numbers is k^2
19oshawott98
2012-03-17 19:07:55
1+3+5...+21=121
1+3+5...+21=121
va2010
2012-03-17 19:07:55
121 means 1+3......+21
121 means 1+3......+21
mcdonalds106_7
2012-03-17 19:07:55
so their must be 11 terms since 11^2=121
so their must be 11 terms since 11^2=121
DPatrick
2012-03-17 19:08:38
This means that the sequence has 11 terms.
This means that the sequence has 11 terms.
jeff10
2012-03-17 19:09:04
Then do 715/11=65, so that's the middle term.
Then do 715/11=65, so that's the middle term.
19oshawott98
2012-03-17 19:09:04
715/11=65
715/11=65
Iggy Iguana
2012-03-17 19:09:04
so the middle integer is 715/11=65
so the middle integer is 715/11=65
19oshawott98
2012-03-17 19:09:04
65 is middle term because 715/11=65
65 is middle term because 715/11=65
prezcoin
2012-03-17 19:09:04
first + middle + last terms = 3 * middle term
first + middle + last terms = 3 * middle term
DPatrick
2012-03-17 19:09:19
Exactly. We finish by using a couple of facts about arithmetic series.
Exactly. We finish by using a couple of facts about arithmetic series.
DPatrick
2012-03-17 19:09:42
Since the sum of the sequence is 715 and there are 11 terms, the average term is 715/11 = 65.
Since the sum of the sequence is 715 and there are 11 terms, the average term is 715/11 = 65.
DPatrick
2012-03-17 19:10:02
The middle term equals the average term, 65.
The middle term equals the average term, 65.
KeepingItReal
2012-03-17 19:10:09
first + last term = 130
first + last term = 130
DPatrick
2012-03-17 19:10:12
The first and last terms sum to twice the average term, or 2*65 = 130.
The first and last terms sum to twice the average term, or 2*65 = 130.
andrewjjiang97
2012-03-17 19:10:23
65+130=195
65+130=195
DPatrick
2012-03-17 19:11:06
This problem is mostly a matter of carefully keeping track of our choices as we construct a possible serving.
This problem is mostly a matter of carefully keeping track of our choices as we construct a possible serving.
Iggy Iguana
2012-03-17 19:11:27
there are 9 choices of who gets correct meal
there are 9 choices of who gets correct meal
andrewjjiang97
2012-03-17 19:11:27
calculate for one person
calculate for one person
KeepingItReal
2012-03-17 19:11:27
9 ways to choose the person with correct order.
9 ways to choose the person with correct order.
mcdonalds106_7
2012-03-17 19:11:27
It is symmetric for the 9 people, so assume one person has his own meal and multiply by 9 at the end
It is symmetric for the 9 people, so assume one person has his own meal and multiply by 9 at the end
DPatrick
2012-03-17 19:11:33
Right. We need to pick one person to receive their correct order. There are 9 choices.
Right. We need to pick one person to receive their correct order. There are 9 choices.
DPatrick
2012-03-17 19:11:50
Without loss of generality, we can suppose it's any person. We'll count how many ways we can finish the serving, then multiply by 9 (for the 9 choices of which person gets their order) to get our final answer.
Without loss of generality, we can suppose it's any person. We'll count how many ways we can finish the serving, then multiply by 9 (for the 9 choices of which person gets their order) to get our final answer.
DPatrick
2012-03-17 19:12:01
So I made a little chart to help me keep track of things:
So I made a little chart to help me keep track of things:
DPatrick
2012-03-17 19:12:16
Notice I've arbitrarily got one beef person getting their correct meal.
Notice I've arbitrarily got one beef person getting their correct meal.
DPatrick
2012-03-17 19:12:18
Now what>?
Now what>?
andrewjjiang97
2012-03-17 19:12:33
The other two B's can go under CC, CF, or FF
The other two B's can go under CC, CF, or FF
fireonice
2012-03-17 19:12:33
the other two Bs can get both C, both F, or one C and one F
the other two Bs can get both C, both F, or one C and one F
jubjubdaboss
2012-03-17 19:12:33
there are three cases for the other two B's: F and C, 2 F's, or 2C's
there are three cases for the other two B's: F and C, 2 F's, or 2C's
DPatrick
2012-03-17 19:12:44
Right. The other two Bs can go to 2 of the C people, 2 of the F people, or one each to a C and an F.
Right. The other two Bs can go to 2 of the C people, 2 of the F people, or one each to a C and an F.
FalconPower
2012-03-17 19:12:52
casework
casework
19oshawott98
2012-03-17 19:12:52
case work?
case work?
joshxiong
2012-03-17 19:12:52
Casework.
Casework.
ahaanomegas
2012-03-17 19:12:52
Casework
Casework
DPatrick
2012-03-17 19:12:57
Now we have casework. :)
Now we have casework. :)
DPatrick
2012-03-17 19:13:06
If they go to 2 C people, how many choices are there?
If they go to 2 C people, how many choices are there?
va2010
2012-03-17 19:13:37
3C2=3
3C2=3
Hydroxide
2012-03-17 19:13:37
3
3
joshxiong
2012-03-17 19:13:37
3C2=3
3C2=3
alligator112
2012-03-17 19:13:37
3 choices for the 2C, only 1 way for the rest
3 choices for the 2C, only 1 way for the rest
keelan32
2012-03-17 19:13:37
3 choices for the two C
3 choices for the two C
DPatrick
2012-03-17 19:13:45
There are C(3,2) = 3 choices of two C people. (Or, think of choosing one of the 3 C people to NOT get beef.)
There are C(3,2) = 3 choices of two C people. (Or, think of choosing one of the 3 C people to NOT get beef.)
DPatrick
2012-03-17 19:13:52
Suppose without loss of generality that it's the first two:
Suppose without loss of generality that it's the first two:
DPatrick
2012-03-17 19:14:02
In how many ways can we finish from here?
In how many ways can we finish from here?
lucylai
2012-03-17 19:14:19
the remaining beef people must receive fish
the remaining beef people must receive fish
alcra
2012-03-17 19:14:20
Now the others have only 1 choice.
Now the others have only 1 choice.
alligator112
2012-03-17 19:14:20
B, B, and C must get F, the 3 F's must get C
B, B, and C must get F, the 3 F's must get C
DPatrick
2012-03-17 19:14:26
The finish is actually forced: the three fishes must go to the three-remaining non-fish people, and the chickens to the fish people:
The finish is actually forced: the three fishes must go to the three-remaining non-fish people, and the chickens to the fish people:
DPatrick
2012-03-17 19:14:48
So there are 3 possibilities in the "2 B's go to 2 C's case".
So there are 3 possibilities in the "2 B's go to 2 C's case".
Iggy Iguana
2012-03-17 19:15:03
this is also the case with both under f
this is also the case with both under f
va2010
2012-03-17 19:15:03
the 2 F people is symmetrical
the 2 F people is symmetrical
fractals
2012-03-17 19:15:03
2C's and 2F's are the same by symmetry.
2C's and 2F's are the same by symmetry.
mcdonalds106_7
2012-03-17 19:15:03
same for 2Bs go to 2Fs case
same for 2Bs go to 2Fs case
DPatrick
2012-03-17 19:15:24
Good -- by symmetry, the "2 B's to 2 F's" case is the same as the previous case. So there are 3 possibilities in this case too.
Good -- by symmetry, the "2 B's to 2 F's" case is the same as the previous case. So there are 3 possibilities in this case too.
esiegel
2012-03-17 19:15:44
but what about... C AND F?
but what about... C AND F?
mcdonalds106_7
2012-03-17 19:15:44
now the hard case- one F and one C
now the hard case- one F and one C
NextEinstein
2012-03-17 19:15:44
then 1 to C, 1 to F
then 1 to C, 1 to F
DPatrick
2012-03-17 19:15:50
How about the "1 B to each a C and an F"?
How about the "1 B to each a C and an F"?
DPatrick
2012-03-17 19:16:05
First, how many choices for where the two remaining B's go?
First, how many choices for where the two remaining B's go?
lucylai
2012-03-17 19:16:24
3*3=9
3*3=9
Hydroxide
2012-03-17 19:16:24
3*3
3*3
alcra
2012-03-17 19:16:24
Of the C people, one must get a B, and of the F people, one must get a B, so 9 choices here.
Of the C people, one must get a B, and of the F people, one must get a B, so 9 choices here.
aopsmomisawesome
2012-03-17 19:16:24
3x3=9
3x3=9
othuum0149
2012-03-17 19:16:24
3*3=9
3*3=9
DPatrick
2012-03-17 19:16:29
We have 3 choices for which C, and 3 choices for which F, so there are 3*3 = 9 ways to assign the two B's.
We have 3 choices for which C, and 3 choices for which F, so there are 3*3 = 9 ways to assign the two B's.
DPatrick
2012-03-17 19:16:35
Now we're at this point:
Now we're at this point:
DPatrick
2012-03-17 19:17:05
In how many ways can we finish?
In how many ways can we finish?
19oshawott98
2012-03-17 19:17:51
f and c must go to the remaining Bs
f and c must go to the remaining Bs
mathswimmer
2012-03-17 19:17:51
C must fill up the Fish, and then 2 choices for which B to go to
C must fill up the Fish, and then 2 choices for which B to go to
alcra
2012-03-17 19:17:51
Two, since the B people need one C one F
Two, since the B people need one C one F
DPatrick
2012-03-17 19:17:59
It's clear that the two other C people must receive fish, and the two other F people must receive chicken:
It's clear that the two other C people must receive fish, and the two other F people must receive chicken:
DPatrick
2012-03-17 19:18:13
So that leaves to decide which B person remaining gets C and which gets F. That's 2 possibilities.
So that leaves to decide which B person remaining gets C and which gets F. That's 2 possibilities.
DPatrick
2012-03-17 19:18:43
So there are 9*2 = 18 possibilities in this case. (9 choices for the 2 Bs then 2 choices to finish)
So there are 9*2 = 18 possibilities in this case. (9 choices for the 2 Bs then 2 choices to finish)
lucylai
2012-03-17 19:18:57
total is 9(3+3+18)=216
total is 9(3+3+18)=216
joshxiong
2012-03-17 19:18:57
9*(3+3+3*3*2)=216
9*(3+3+3*3*2)=216
AlcumusGuy
2012-03-17 19:18:57
add them up and multiply by 9
add them up and multiply by 9
DPatrick
2012-03-17 19:19:02
Adding the cases gives 3+3+18 = 24 ways to finish after we choose the diner who gets their correct order.
Adding the cases gives 3+3+18 = 24 ways to finish after we choose the diner who gets their correct order.
DPatrick
2012-03-17 19:19:29
(remember that the 9 came from the 9 choices of which diner got their order correct.)
(remember that the 9 came from the 9 choices of which diner got their order correct.)
DPatrick
2012-03-17 19:20:04
And now what I'm sure was everyone's favorite...
And now what I'm sure was everyone's favorite...
DPatrick
2012-03-17 19:20:32
Of course, with this problem, the first step is reading it over and over to be sure that you understand what's going on.
Of course, with this problem, the first step is reading it over and over to be sure that you understand what's going on.
DPatrick
2012-03-17 19:20:41
...and then read it again to be SURE you got everything.
...and then read it again to be SURE you got everything.
DPatrick
2012-03-17 19:20:47
What facts can we learn from the problem statement?
What facts can we learn from the problem statement?
mastermang02
2012-03-17 19:21:21
Horse mile time=10 minutes, Butch mile time=15 minutes, Sundance mile time=24 minutes:bow:
Horse mile time=10 minutes, Butch mile time=15 minutes, Sundance mile time=24 minutes:bow:
jaw
2012-03-17 19:21:21
When one is walking, the other is riding.
When one is walking, the other is riding.
andrewjjiang97
2012-03-17 19:21:21
sparky goes 10 min mile, butch 15, sundance 24
sparky goes 10 min mile, butch 15, sundance 24
DPatrick
2012-03-17 19:21:26
It takes Butch 15 minutes to walk between mileposts.
It takes Butch 15 minutes to walk between mileposts.
DPatrick
2012-03-17 19:21:32
It takes Sundance 24 minutes to walk between mileposts.
It takes Sundance 24 minutes to walk between mileposts.
DPatrick
2012-03-17 19:21:37
It takes either of them 10 minutes to ride the horse between mileposts.
It takes either of them 10 minutes to ride the horse between mileposts.
DPatrick
2012-03-17 19:21:44
Between any two posts, exactly one of them will be walking and one of them will be riding the horse.
Between any two posts, exactly one of them will be walking and one of them will be riding the horse.
DPatrick
2012-03-17 19:22:06
Now you could just work out what happens by brute force, but let's look for a slick solution.
Now you could just work out what happens by brute force, but let's look for a slick solution.
ProblemSolver1026
2012-03-17 19:22:33
Set a system of equations.
Set a system of equations.
mathgiraffe
2012-03-17 19:22:33
let the number of miles Butch rides the horse be a and the number of miles Sundance rides be b.
let the number of miles Butch rides the horse be a and the number of miles Sundance rides be b.
DPatrick
2012-03-17 19:22:42
I like this idea, but I have better variables. :)
I like this idea, but I have better variables. :)
fractals
2012-03-17 19:23:07
b + s = n
b + s = n
Mary_Posa
2012-03-17 19:23:07
b+s=n
b+s=n
esiegel
2012-03-17 19:23:07
s+b = n
s+b = n
mathgiraffe
2012-03-17 19:23:07
b+s is the total distance
b+s is the total distance
alligator112
2012-03-17 19:23:32
butch rides s miles, sundance rides b miles
butch rides s miles, sundance rides b miles
FalconPower
2012-03-17 19:23:32
butch rides for s miles and sundance rides for b
butch rides for s miles and sundance rides for b
aopsmomisawesome
2012-03-17 19:23:32
butch rides for s miles and sundance rides for b miles
butch rides for s miles and sundance rides for b miles
jubjubdaboss
2012-03-17 19:24:17
we can write equations for the time it takes them
we can write equations for the time it takes them
DPatrick
2012-03-17 19:24:40
Exactly. And we know that the time it takes them to travel the n miles is equal. So we write expressions for how long it takes each of them to travel the n miles, and set them equal.
Exactly. And we know that the time it takes them to travel the n miles is equal. So we write expressions for how long it takes each of them to travel the n miles, and set them equal.
alligator112
2012-03-17 19:25:06
15b +10s = 10b + 24s
15b +10s = 10b + 24s
Iggy Iguana
2012-03-17 19:25:06
15b+10s=24s+10b
15b+10s=24s+10b
superpi83
2012-03-17 19:25:06
Butch: 15b+10s; Sundance: 10b+24s
Butch: 15b+10s; Sundance: 10b+24s
scgorantla
2012-03-17 19:26:02
therfore 5b=14s
therfore 5b=14s
centrino
2012-03-17 19:26:02
5b=14s
5b=14s
cstbear
2012-03-17 19:26:02
so we have 5b=14s
so we have 5b=14s
lucylai
2012-03-17 19:26:02
5b=14s
5b=14s
joshxiong
2012-03-17 19:26:02
Thus 5b=14s.
Thus 5b=14s.
googol.plex
2012-03-17 19:26:28
b and s are integers and they are as small as possible, so b=14 and s=5
b and s are integers and they are as small as possible, so b=14 and s=5
fractals
2012-03-17 19:26:28
b = 14, s = 5 to get the smallest
b = 14, s = 5 to get the smallest
lucylai
2012-03-17 19:26:28
least possible values are b=14 and s=5
least possible values are b=14 and s=5
fireonice
2012-03-17 19:26:28
they meet for the first time at 19 miles
they meet for the first time at 19 miles
centrino
2012-03-17 19:26:28
First time they meet would be when b=14, s=5
First time they meet would be when b=14, s=5
DPatrick
2012-03-17 19:26:41
Right. The smallest solution in positive integers is b=14 and s=5. (Since 5 and 14 are relatively prime.)
Right. The smallest solution in positive integers is b=14 and s=5. (Since 5 and 14 are relatively prime.)
DPatrick
2012-03-17 19:26:49
That is, they travel 19 miles, where Butch walks 14 and Sundance walks 5.
That is, they travel 19 miles, where Butch walks 14 and Sundance walks 5.
mcdonalds106_7
2012-03-17 19:26:59
now we plug it in
now we plug it in
fractals
2012-03-17 19:27:02
So n = 19 and t = 260
So n = 19 and t = 260
algebra1337
2012-03-17 19:27:35
but how do we know that they will meet first at 19 miles, and not 38 or something?
but how do we know that they will meet first at 19 miles, and not 38 or something?
DPatrick
2012-03-17 19:27:46
That is an excellent question. How can we be sure that our solution to the equation is actually possible? That is, how can we be sure that the horse-swapping occurs correctly so that this 19-mile trek is actually achievable under the travel rules laid out in the problem?
That is an excellent question. How can we be sure that our solution to the equation is actually possible? That is, how can we be sure that the horse-swapping occurs correctly so that this 19-mile trek is actually achievable under the travel rules laid out in the problem?
lucylai
2012-03-17 19:28:09
bash!!!
bash!!!
va2010
2012-03-17 19:28:09
Brute Force!
Brute Force!
FalconPower
2012-03-17 19:28:09
BASH IT?!?!?
BASH IT?!?!?
scgorantla
2012-03-17 19:28:09
by plugging it back in
by plugging it back in
m1sterzer0
2012-03-17 19:28:09
you bash it out anyway to check your answer :p
you bash it out anyway to check your answer :p
DPatrick
2012-03-17 19:28:20
We can actually check it rather quickly. (You might have also solved the problem in the first place using the method that I'm about to describe as our "check".)
We can actually check it rather quickly. (You might have also solved the problem in the first place using the method that I'm about to describe as our "check".)
DPatrick
2012-03-17 19:28:31
Note that, on any mile, if Sundance rides and Butch walks, Sundance gains 5 minutes on Butch (as it only takes him 10 minutes to ride versus Butch's 15 minutes to walk).
Note that, on any mile, if Sundance rides and Butch walks, Sundance gains 5 minutes on Butch (as it only takes him 10 minutes to ride versus Butch's 15 minutes to walk).
DPatrick
2012-03-17 19:28:45
On the other hand, if Butch rides and Sundance walks, then Butch gains 14 minutes on Sundance.
On the other hand, if Butch rides and Sundance walks, then Butch gains 14 minutes on Sundance.
DPatrick
2012-03-17 19:28:54
And at each milepost, whichever of them is behind (in time) gets to ride.
And at each milepost, whichever of them is behind (in time) gets to ride.
DPatrick
2012-03-17 19:29:05
So we can quickly check how many minutes Sundance arrives before Butch at each milepost (where a negative number means that Butch arrives before Sundance by that many minutes):
So we can quickly check how many minutes Sundance arrives before Butch at each milepost (where a negative number means that Butch arrives before Sundance by that many minutes):
DPatrick
2012-03-17 19:29:08
0, 5, -9, -4, 1, -13, -8, -3, 2, -12, -7, -2, 3, -11, -6, -1, 4, -10, -5, 0.
0, 5, -9, -4, 1, -13, -8, -3, 2, -12, -7, -2, 3, -11, -6, -1, 4, -10, -5, 0.
DPatrick
2012-03-17 19:29:24
At the start and at each negative number, S is behind, so S rides and B walks, and S gains 5 minutes.
At each positive number, S is ahead, so S walks and B rides, and S loses 14 minutes.
At the start and at each negative number, S is behind, so S rides and B walks, and S gains 5 minutes.
At each positive number, S is ahead, so S walks and B rides, and S loses 14 minutes.
DPatrick
2012-03-17 19:29:36
We indeed check and see that after 19 miles, S and B are back even with each other.
We indeed check and see that after 19 miles, S and B are back even with each other.
proglote
2012-03-17 19:30:05
can we use a graph to solve it, too?
can we use a graph to solve it, too?
DPatrick
2012-03-17 19:30:10
Certainly.
Certainly.
DPatrick
2012-03-17 19:30:50
Like a lot of AIME problems, this is actually pretty easy once you decode the problem statement.
Like a lot of AIME problems, this is actually pretty easy once you decode the problem statement.
DPatrick
2012-03-17 19:30:59
What are we really counting here?
What are we really counting here?
richard4912
2012-03-17 19:31:28
binary numbers that are one apart
binary numbers that are one apart
deepankar
2012-03-17 19:31:28
pairs of consecutive numbers
pairs of consecutive numbers
geyser
2012-03-17 19:31:28
the groups of numbers that are 1 apart
the groups of numbers that are 1 apart
mcdonalds106_7
2012-03-17 19:31:28
number of consecutive integers that use 5 zeroes and 8 ones
number of consecutive integers that use 5 zeroes and 8 ones
DPatrick
2012-03-17 19:31:33
Right. We're counting numbers in B to which we can add 1 and still get a number of B.
Right. We're counting numbers in B to which we can add 1 and still get a number of B.
DPatrick
2012-03-17 19:31:43
When we add 1 to a binary number, when do we not change the number of 0s and 1s (assuming we have the leading zeros like in this problem)?
When we add 1 to a binary number, when do we not change the number of 0s and 1s (assuming we have the leading zeros like in this problem)?
Mr.117
2012-03-17 19:32:07
when it is 01 to 10
when it is 01 to 10
algebra1337
2012-03-17 19:32:07
when the last two digits are 01
when the last two digits are 01
kelleyzhao
2012-03-17 19:32:07
If the number ends with 01
If the number ends with 01
Hydroxide
2012-03-17 19:32:07
when the last two digits is 01
when the last two digits is 01
AwesomeToad
2012-03-17 19:32:07
____01 -> ______10
____01 -> ______10
thecmd999
2012-03-17 19:32:07
when the last two digits are 01
when the last two digits are 01
DPatrick
2012-03-17 19:32:17
Right. Let's step through this to be sure.
Right. Let's step through this to be sure.
DPatrick
2012-03-17 19:32:23
If the number ends in a 0, then adding 1 just changes the last 0 to a 1, so that doesn't work (we get one additional 1 and one fewer 0).
If the number ends in a 0, then adding 1 just changes the last 0 to a 1, so that doesn't work (we get one additional 1 and one fewer 0).
DPatrick
2012-03-17 19:32:32
If the number ends in 01, we're good! The 01 becomes 10 in the new number, and nothing else changes.
If the number ends in 01, we're good! The 01 becomes 10 in the new number, and nothing else changes.
DPatrick
2012-03-17 19:32:41
If the number ends in more than one 1, what happens?
If the number ends in more than one 1, what happens?
Relativity1618
2012-03-17 19:33:02
ends in 00
ends in 00
CantonMathGuy
2012-03-17 19:33:02
they all become 0s
they all become 0s
scgorantla
2012-03-17 19:33:02
more zeroes appear
more zeroes appear
infinity1
2012-03-17 19:33:02
at least two ones become one one
at least two ones become one one
himym83
2012-03-17 19:33:02
number of 1s go down
number of 1s go down
ImAPerson
2012-03-17 19:33:02
they will turn to 0 when 1 is added
they will turn to 0 when 1 is added
DPatrick
2012-03-17 19:33:20
Right. After we carry the addition, those "more than one 1" all become 0 and the rightmost 0 becomes a 1.
Right. After we carry the addition, those "more than one 1" all become 0 and the rightmost 0 becomes a 1.
DPatrick
2012-03-17 19:33:34
But that's a net loss of more than one 1s and a gain of just one 0. So that doesn't work either.
But that's a net loss of more than one 1s and a gain of just one 0. So that doesn't work either.
va2010
2012-03-17 19:33:42
so it has to end with 01
so it has to end with 01
DPatrick
2012-03-17 19:33:50
Right. We've learned that we just need to count the numbers in B that end in 01.
Right. We've learned that we just need to count the numbers in B that end in 01.
joshxiong
2012-03-17 19:34:07
So we need to count the number of ways to arrange 4 ones and 7 zeroes.
So we need to count the number of ways to arrange 4 ones and 7 zeroes.
scgorantla
2012-03-17 19:34:07
that makes 7 ones and 4 zeroes left
that makes 7 ones and 4 zeroes left
DPatrick
2012-03-17 19:34:11
The other eleven digits are 4 zeros and 7 ones, in any order.
The other eleven digits are 4 zeros and 7 ones, in any order.
lucylai
2012-03-17 19:34:24
answer is just 11C4=330
answer is just 11C4=330
Relativity1618
2012-03-17 19:34:24
11C4=330
11C4=330
Lalagato
2012-03-17 19:34:24
11C4 = 330
11C4 = 330
negativebplusorminus
2012-03-17 19:34:24
C(11,4)=330
C(11,4)=330
DPatrick
2012-03-17 19:35:13
On to by far my least favorite question...
On to by far my least favorite question...
DPatrick
2012-03-17 19:35:31
How do we proceed?
How do we proceed?
centrino
2012-03-17 19:35:47
Substitue z^13 for w in second equation
Substitue z^13 for w in second equation
himym83
2012-03-17 19:35:47
substitute z in for w
substitute z in for w
fractals
2012-03-17 19:35:47
z^143 = z by substitution
z^143 = z by substitution
alligator112
2012-03-17 19:35:47
z^143 = z
z^143 = z
jubjubdaboss
2012-03-17 19:35:47
z=(z^13)^11
z=(z^13)^11
va2010
2012-03-17 19:36:16
z^142=1
z^142=1
FalconPower
2012-03-17 19:36:17
z^142=1
z^142=1
esiegel
2012-03-17 19:36:17
z^142 = 1
z^142 = 1
alcra
2012-03-17 19:36:17
1=z^142
1=z^142
superpi83
2012-03-17 19:36:56
so z=cis(2k*pi/142)
so z=cis(2k*pi/142)
djmathman
2012-03-17 19:36:56
All roots of unity can be written as cis(pin/71) for some n. Hence 71 is our answer.
All roots of unity can be written as cis(pin/71) for some n. Hence 71 is our answer.
scgorantla
2012-03-17 19:36:56
so 2pi(i)/142
so 2pi(i)/142
CantonMathGuy
2012-03-17 19:36:56
imaginary part = sin (pi * x / 71)
imaginary part = sin (pi * x / 71)
alcra
2012-03-17 19:37:51
Our final answer is 71.
Our final answer is 71.
lucylai
2012-03-17 19:37:52
71 is prime, so it never changes
71 is prime, so it never changes
aopsmomisawesome
2012-03-17 19:37:52
71 is prime
71 is prime
centrino
2012-03-17 19:37:52
71 is prime
71 is prime
scgorantla
2012-03-17 19:37:52
so n is 071 no matter what
so n is 071 no matter what
mcdonalds106_7
2012-03-17 19:37:52
but 71 is prime and k<71 so the numerator and denominator are relatively prime, so the answer is 071
but 71 is prime and k<71 so the numerator and denominator are relatively prime, so the answer is 071
DPatrick
2012-03-17 19:38:11
Right. It doesn't matter what k is: since 71 is prime, we cannot reduce the denominator. (Except to 1, if k=71, but that's not allowed by the problem statement.)
Right. It doesn't matter what k is: since 71 is prime, we cannot reduce the denominator. (Except to 1, if k=71, but that's not allowed by the problem statement.)
iwantcombo
2012-03-17 19:38:20
why was this your least favorite question?
why was this your least favorite question?
Binomial-theorem
2012-03-17 19:38:25
This was one of those you know it or you don't questions.
This was one of those you know it or you don't questions.
DPatrick
2012-03-17 19:38:41
Exactly. I found this problem unpleasing. If you know roots of unity, it should have been very, very easy. If you don't, it's pretty much impossible. What I didn't like is that there's not much "problem solving" -- it's just an exercise with complex numbers and roots of unity.
Exactly. I found this problem unpleasing. If you know roots of unity, it should have been very, very easy. If you don't, it's pretty much impossible. What I didn't like is that there's not much "problem solving" -- it's just an exercise with complex numbers and roots of unity.
FalconPower
2012-03-17 19:38:59
like homework almost
like homework almost
DPatrick
2012-03-17 19:39:17
Right, if you've had a trig/complex numbers class (or learned it on your own), this problem is just a homework exercise.
Right, if you've had a trig/complex numbers class (or learned it on your own), this problem is just a homework exercise.
DPatrick
2012-03-17 19:39:25
Fortunately, the next problem is more interesting!
Fortunately, the next problem is more interesting!
DPatrick
2012-03-17 19:39:53
If you stare at the picture a little while, what do you notice?
If you stare at the picture a little while, what do you notice?
noedne
2012-03-17 19:40:13
there are three rings of five around the center
there are three rings of five around the center
DPatrick
2012-03-17 19:40:29
The students appear to be in four "rings". I've shaded the rings in the picture below:
The students appear to be in four "rings". I've shaded the rings in the picture below:
DPatrick
2012-03-17 19:41:21
Each student only gives and receive coins from its adjacent rings, and within its own ring (in the case of the outer green ring).
Each student only gives and receive coins from its adjacent rings, and within its own ring (in the case of the outer green ring).
ABCDE
2012-03-17 19:42:32
We can assign variables for each color.
We can assign variables for each color.
DPatrick
2012-03-17 19:43:12
Sorry, I need to take a short 2-3 minute break...it's pouring rain and our roof is leaking! :(
Sorry, I need to take a short 2-3 minute break...it's pouring rain and our roof is leaking! :(
DPatrick
2012-03-17 19:43:16
Back in 2-3 minutes...
Back in 2-3 minutes...
DPatrick
2012-03-17 19:44:12
Sorry about that. I put a bucket under it.
Sorry about that. I put a bucket under it.
DPatrick
2012-03-17 19:44:26
Back to our problem...
Back to our problem...
DPatrick
2012-03-17 19:44:48
Let's start at the outside and work in. How are g and b related?
Let's start at the outside and work in. How are g and b related?
mastermang02
2012-03-17 19:45:16
g=b
g=b
theone142857
2012-03-17 19:45:16
g=b
g=b
othuum0149
2012-03-17 19:45:16
they're equal
they're equal
mastermang02
2012-03-17 19:45:16
g=b since they both give 1/4 of their coins to each other:rose:
g=b since they both give 1/4 of their coins to each other:rose:
DPatrick
2012-03-17 19:45:41
I can't really say if all the individual greens and blues are equal (it appears they might be, but we can't prove that).
I can't really say if all the individual greens and blues are equal (it appears they might be, but we can't prove that).
DPatrick
2012-03-17 19:46:02
But as a group, the green students give half their coins to each other, and half their coins to the students in the blue ring.
But as a group, the green students give half their coins to each other, and half their coins to the students in the blue ring.
DPatrick
2012-03-17 19:46:22
On the other hand, the students in the blue ring also give half their coins to the students in the green ring.
On the other hand, the students in the blue ring also give half their coins to the students in the green ring.
DPatrick
2012-03-17 19:46:31
And for the number of coins for each student to remain equal, we must have
(green -> blue coins) = (blue -> green coins).
And for the number of coins for each student to remain equal, we must have
(green -> blue coins) = (blue -> green coins).
DPatrick
2012-03-17 19:46:42
The total number of coins in the green ring equals the total number of coins in the blue ring. Thus g=b.
The total number of coins in the green ring equals the total number of coins in the blue ring. Thus g=b.
DPatrick
2012-03-17 19:47:14
How are b and r related?
How are b and r related?
mastermang02
2012-03-17 19:47:34
1/2b=2/3r
1/2b=2/3r
theone142857
2012-03-17 19:47:34
4r=3b
4r=3b
aopsmomisawesome
2012-03-17 19:47:34
r = 3b/4
r = 3b/4
googol.plex
2012-03-17 19:47:34
r=3/4b
r=3/4b
Relativity1618
2012-03-17 19:47:34
4r=3b
4r=3b
DPatrick
2012-03-17 19:47:43
The blue ring gives half its coins to the red ring. The red ring gives 2/3 of its coins to the blue ring.
The blue ring gives half its coins to the red ring. The red ring gives 2/3 of its coins to the blue ring.
DPatrick
2012-03-17 19:48:20
Finally, how are r and w related?
Finally, how are r and w related?
fractals
2012-03-17 19:48:43
1/3r = w
1/3r = w
proglote
2012-03-17 19:48:43
1/3 r = w
1/3 r = w
aussiedoodle
2012-03-17 19:48:43
r/3 = w
r/3 = w
DPatrick
2012-03-17 19:49:01
The red ring gives 1/3 of its coins to the person in white in the middle. This must equal what that person starts with.
The red ring gives 1/3 of its coins to the person in white in the middle. This must equal what that person starts with.
Relativity1618
2012-03-17 19:49:09
substitute and solve for w
substitute and solve for w
DPatrick
2012-03-17 19:49:18
We have r = 3w, and b = (4/3)r = 4w, and g = b = 4w.
We have r = 3w, and b = (4/3)r = 4w, and g = b = 4w.
aopsmomisawesome
2012-03-17 19:49:46
Thus, w=280, and the answer is 280
Thus, w=280, and the answer is 280
fractals
2012-03-17 19:49:46
12w = 3360, so w = 280
12w = 3360, so w = 280
esiegel
2012-03-17 19:49:46
3360/12 good job!
3360/12 good job!
DPatrick
2012-03-17 19:50:16
Notice I solved the problem without assuming any symmetry (that is, without assuming that all the green circles were equal).
Notice I solved the problem without assuming any symmetry (that is, without assuming that all the green circles were equal).
DPatrick
2012-03-17 19:50:42
You could assume symmetry and proceed from there. It might be a little quicker but it doesn't necessarily cover all the cases.
You could assume symmetry and proceed from there. It might be a little quicker but it doesn't necessarily cover all the cases.
DPatrick
2012-03-17 19:50:56
However, since the problem implies a unique answer, it's a legitimate strategy.
However, since the problem implies a unique answer, it's a legitimate strategy.
DPatrick
2012-03-17 19:51:48
We have three points where the plane hits edges the cube. What else should we add to have a complete picture of how the plane intersects the cube?
We have three points where the plane hits edges the cube. What else should we add to have a complete picture of how the plane intersects the cube?
centrino
2012-03-17 19:52:05
Find where plane intersects FB
Find where plane intersects FB
Yongyi781
2012-03-17 19:52:06
The first thing you want to find is where the plane intersects FB
The first thing you want to find is where the plane intersects FB
yankeefan6795
2012-03-17 19:52:06
point on fb
point on fb
mcdonalds106_7
2012-03-17 19:52:06
where it intersects FB
where it intersects FB
NewAlbionAcademy
2012-03-17 19:52:06
Where it intersects with FB
Where it intersects with FB
ngahlot
2012-03-17 19:52:06
point on FB
point on FB
DPatrick
2012-03-17 19:52:13
We should include the other intersection point of the cube's edges and the plane:
We should include the other intersection point of the cube's edges and the plane:
DPatrick
2012-03-17 19:52:23
We know all about M and N. How will we learn about Q?
We know all about M and N. How will we learn about Q?
Relativity1618
2012-03-17 19:52:57
extend the smaller solid
extend the smaller solid
Relativity1618
2012-03-17 19:52:57
extend NQ
extend NQ
DPatrick
2012-03-17 19:53:11
Right. It'd be nice to know where DM and NQ intersect.
Right. It'd be nice to know where DM and NQ intersect.
DPatrick
2012-03-17 19:53:45
One thought is that NQ and BC must intersect somewhere, since they're both in plane BCGF and they're not parallel. That relates Q to points we know about: N, B, C.
One thought is that NQ and BC must intersect somewhere, since they're both in plane BCGF and they're not parallel. That relates Q to points we know about: N, B, C.
DPatrick
2012-03-17 19:53:55
Another thought is that DM and NQ intersect somewhere, since they're both in plane DMQN, and they're not parallel. That relates Q to points we know about: D, M, and N.
Another thought is that DM and NQ intersect somewhere, since they're both in plane DMQN, and they're not parallel. That relates Q to points we know about: D, M, and N.
accents
2012-03-17 19:54:14
Is the intersection on the line BC?
Is the intersection on the line BC?
DPatrick
2012-03-17 19:54:34
How do we know this for sure?
How do we know this for sure?
fmasroor
2012-03-17 19:54:44
yes since dm is entirely on abcd
yes since dm is entirely on abcd
timelessmath
2012-03-17 19:54:49
yes because QN and BC are on the same plane
yes because QN and BC are on the same plane
DPatrick
2012-03-17 19:54:57
Right. Combine these last two comments and we have what we need.
Right. Combine these last two comments and we have what we need.
DPatrick
2012-03-17 19:55:13
DM and BC intersect in the plane ABCD.
DM and BC intersect in the plane ABCD.
DPatrick
2012-03-17 19:55:25
NQ and BC intersect in the place BCGF.
NQ and BC intersect in the place BCGF.
DPatrick
2012-03-17 19:55:32
Those planes intersect in the line BC>
Those planes intersect in the line BC>
DPatrick
2012-03-17 19:56:02
So the plane (DMQN that we're chopping by) intersects the line BC at a point that DM, NQ, and BC all pass through.
So the plane (DMQN that we're chopping by) intersects the line BC at a point that DM, NQ, and BC all pass through.
DPatrick
2012-03-17 19:56:29
So using this picture, how can we describe the area inside the cube underneath the plane?
So using this picture, how can we describe the area inside the cube underneath the plane?
fractals
2012-03-17 19:56:58
A frustum of a pyramid
A frustum of a pyramid
lucylai
2012-03-17 19:56:58
it's a truncated pyramid
it's a truncated pyramid
Relativity1618
2012-03-17 19:56:58
frustrum?
frustrum?
sigma96
2012-03-17 19:56:58
a frustrum
a frustrum
DPatrick
2012-03-17 19:57:16
Right! The big shape PCND is a pyramid with base DCN and vertex P.
Right! The big shape PCND is a pyramid with base DCN and vertex P.
DPatrick
2012-03-17 19:57:41
We then chop off the smaller pyramid PMBQ to get the part of the cube under the cutting plane.
We then chop off the smaller pyramid PMBQ to get the part of the cube under the cutting plane.
DPatrick
2012-03-17 19:57:50
What the size of the smaller pyramid relative to the larger pyramid?
What the size of the smaller pyramid relative to the larger pyramid?
hi how are you doing toda
2012-03-17 19:58:10
1/8
1/8
himym83
2012-03-17 19:58:10
1/8
1/8
Relativity1618
2012-03-17 19:58:10
1/8
1/8
mcdonalds106_7
2012-03-17 19:58:10
1/8
1/8
NewAlbionAcademy
2012-03-17 19:58:10
1/8
1/8
DPatrick
2012-03-17 19:58:32
Right. (I was a little too vague when I used the word "size"...I should have said "volume".)
Right. (I was a little too vague when I used the word "size"...I should have said "volume".)
DPatrick
2012-03-17 19:58:52
Since B is the midpoint of PC, the smaller pyramid has half the edge length of the larger one, so has (1/2)^3=1/8 the volume. Therefore the part of the pyramid that's inside the cube is 7/8 of the large pyramid.
Since B is the midpoint of PC, the smaller pyramid has half the edge length of the larger one, so has (1/2)^3=1/8 the volume. Therefore the part of the pyramid that's inside the cube is 7/8 of the large pyramid.
DPatrick
2012-03-17 19:59:12
What is the volume of the large pyramid?
What is the volume of the large pyramid?
dooba
2012-03-17 19:59:22
Why is B the midpoint of PC?
Why is B the midpoint of PC?
Hydroxide
2012-03-17 19:59:22
how do you know that B is the midpoint of PC?
how do you know that B is the midpoint of PC?
DPatrick
2012-03-17 19:59:41
We know that M is the midpoint of AB, so it's also the midpoint of DP.
We know that M is the midpoint of AB, so it's also the midpoint of DP.
DPatrick
2012-03-17 20:00:25
And from there we can use similar triangles. (I'll omit the details for right now.)
And from there we can use similar triangles. (I'll omit the details for right now.)
ABCDE
2012-03-17 20:00:45
1/4*2*1/3=1/6
1/4*2*1/3=1/6
scgorantla
2012-03-17 20:00:45
volume of large pyramid is 1/6
volume of large pyramid is 1/6
Iggy Iguana
2012-03-17 20:00:45
volume of big pyramid = 1/4 * 2 / 3 = 1/6
volume of big pyramid = 1/4 * 2 / 3 = 1/6
DPatrick
2012-03-17 20:01:07
The large pyramid has a base with area of triangle DCN, which is 1/4, and its height is PC, which is 2.
The large pyramid has a base with area of triangle DCN, which is 1/4, and its height is PC, which is 2.
Relativity1618
2012-03-17 20:01:21
volume of frustrum=7/8*1/6=7/48
volume of frustrum=7/8*1/6=7/48
googol.plex
2012-03-17 20:01:21
the volume of the chunk inside the cube=7/48
the volume of the chunk inside the cube=7/48
Iggy Iguana
2012-03-17 20:01:47
and thus the big piece is 41/48, giving 089 as answer
and thus the big piece is 41/48, giving 089 as answer
himym83
2012-03-17 20:01:47
thus answer is 41/48 or 89
thus answer is 41/48 or 89
Relativity1618
2012-03-17 20:01:47
subtract frustrum from cube to attain 1-7/48=41/48.41+48=89
subtract frustrum from cube to attain 1-7/48=41/48.41+48=89
theone142857
2012-03-17 20:01:47
volume of bigger portion=1-7/48=41/48
volume of bigger portion=1-7/48=41/48
DPatrick
2012-03-17 20:02:58
How can we approach this?
How can we approach this?
scgorantla
2012-03-17 20:03:35
make each equality equal to a variable, k.
make each equality equal to a variable, k.
himym83
2012-03-17 20:03:35
set the equalities equal to a variable
set the equalities equal to a variable
scgorantla
2012-03-17 20:03:35
make each equality equal to a variable, k.
make each equality equal to a variable, k.
vzl11014
2012-03-17 20:03:35
we can set everything as one variable
we can set everything as one variable
eccfcco15
2012-03-17 20:03:59
log -> exponential
log -> exponential
fmasroor
2012-03-17 20:03:59
get rid of logs
get rid of logs
DPatrick
2012-03-17 20:04:22
What can we do with these equations?
What can we do with these equations?
himym83
2012-03-17 20:04:54
2y*4z=8yz, thus we can use LHS
2y*4z=8yz, thus we can use LHS
scgorantla
2012-03-17 20:04:54
multiply the first two equations
multiply the first two equations
fireonice
2012-03-17 20:04:54
multiply the first two
multiply the first two
turkeybob777
2012-03-17 20:04:54
multiply the first two together
multiply the first two together
DPatrick
2012-03-17 20:05:14
We certainly see that the product of the right sides of the first two gives us the right side of the third.
We certainly see that the product of the right sides of the first two gives us the right side of the third.
DPatrick
2012-03-17 20:05:47
Can we solve for x and/or r using this?
Can we solve for x and/or r using this?
scgorantla
2012-03-17 20:06:12
take the rth root on both sides
take the rth root on both sides
aussiedoodle
2012-03-17 20:06:12
take the rth root of both sides
take the rth root of both sides
vzl11014
2012-03-17 20:06:12
yes, we can take the r root on both sides
yes, we can take the r root on both sides
DPatrick
2012-03-17 20:06:32
Now we can solve for x!
Now we can solve for x!
lucylai
2012-03-17 20:06:43
square both sides
square both sides
mathswimmer
2012-03-17 20:06:43
square both sides 2x^2=4x^8
square both sides 2x^2=4x^8
DPatrick
2012-03-17 20:06:57
(It's OK to do this since everything in sight is positive.)
(It's OK to do this since everything in sight is positive.)
himym83
2012-03-17 20:07:14
x = 2^-1/6
x = 2^-1/6
cstar124
2012-03-17 20:07:17
x^6=1/2
x^6=1/2
DPatrick
2012-03-17 20:07:46
Great, we found x! We're 1/3 of the way there (hopefully). Now what?
Great, we found x! We're 1/3 of the way there (hopefully). Now what?
DPatrick
2012-03-17 20:07:56
Recall our system:
Recall our system:
FalconPower
2012-03-17 20:08:15
plug back in?
plug back in?
scgorantla
2012-03-17 20:08:15
plug in x
plug in x
lucylai
2012-03-17 20:08:15
plug x back in
plug x back in
DPatrick
2012-03-17 20:08:34
I could plug x back in, but let's leave it as "x" for a moment. 2^(-1/6) seems messy to use until we really need it.
I could plug x back in, but let's leave it as "x" for a moment. 2^(-1/6) seems messy to use until we really need it.
DPatrick
2012-03-17 20:09:01
Also note that we've used the information in the 3rd equation already, so it's not going to help us further.
Also note that we've used the information in the 3rd equation already, so it's not going to help us further.
fractals
2012-03-17 20:09:39
Multiply: (first equation)^5*(second equation)
Multiply: (first equation)^5*(second equation)
fireonice
2012-03-17 20:09:39
we need y^5z so let's find that in terms of the equations
we need y^5z so let's find that in terms of the equations
theone142857
2012-03-17 20:09:39
take the first equation to the 5th and multiply the second and x on both sides
take the first equation to the 5th and multiply the second and x on both sides
DPatrick
2012-03-17 20:09:46
Aha! Let's keep our eye on the ball!
Aha! Let's keep our eye on the ball!
DPatrick
2012-03-17 20:09:56
We want the quantity y^5z as part of our final answer, so we can use the first two equations to get it on the right side.
We want the quantity y^5z as part of our final answer, so we can use the first two equations to get it on the right side.
DPatrick
2012-03-17 20:10:03
Specifically, let's raise the first equation to the 5th power and multiply by the second.
Specifically, let's raise the first equation to the 5th power and multiply by the second.
DPatrick
2012-03-17 20:10:27
What does the left side simplify to?
What does the left side simplify to?
FalconPower
2012-03-17 20:10:57
2^(r/2)*x^3r
2^(r/2)*x^3r
calculus17
2012-03-17 20:11:19
plug in for x
plug in for x
DPatrick
2012-03-17 20:11:31
Now seems like a good time to plug in the x -- we've simplified as far as we can.
Now seems like a good time to plug in the x -- we've simplified as far as we can.
lucylai
2012-03-17 20:11:56
it cancels it out
it cancels it out
himym83
2012-03-17 20:11:56
r's cancel when x is plugged back in
r's cancel when x is plugged back in
fireonice
2012-03-17 20:11:56
the left side is 1!
the left side is 1!
calculus17
2012-03-17 20:11:56
1=2^7y^5z
1=2^7y^5z
DPatrick
2012-03-17 20:12:00
Something wonderful happened!
Something wonderful happened!
fractals
2012-03-17 20:12:19
y^5z=2^-7
y^5z=2^-7
lucylai
2012-03-17 20:12:19
y^5*z=2^-7
y^5*z=2^-7
theone142857
2012-03-17 20:12:40
mutiply x on both sides
mutiply x on both sides
coldsummer
2012-03-17 20:12:40
multiply by x
multiply by x
accents
2012-03-17 20:12:44
But don't forget, we're looking for xy^5z, and we have both!@@
But don't forget, we're looking for xy^5z, and we have both!@@
DPatrick
2012-03-17 20:13:54
Again, a lot of words and notation.
Again, a lot of words and notation.
DPatrick
2012-03-17 20:14:03
How can we describe the numbers in S?
How can we describe the numbers in S?
calculus17
2012-03-17 20:14:23
all squares ending in 256
all squares ending in 256
vwu9
2012-03-17 20:14:23
squares that end with 256
squares that end with 256
AlcumusGuy
2012-03-17 20:14:23
perfect squares ending in 256
perfect squares ending in 256
fireonice
2012-03-17 20:14:23
perfect squares that end with 256
perfect squares that end with 256
DPatrick
2012-03-17 20:14:38
How can we algebraically describe a number ending in 256?
How can we algebraically describe a number ending in 256?
Relativity1618
2012-03-17 20:14:56
1000a+256
1000a+256
somanywindows
2012-03-17 20:14:56
1000x + 256
1000x + 256
fractals
2012-03-17 20:14:56
1000n+256
1000n+256
kealand
2012-03-17 20:14:56
1000N + 256
1000N + 256
Relativity1618
2012-03-17 20:15:43
so we do difference of squares
so we do difference of squares
CantonMathGuy
2012-03-17 20:15:43
(k + 16)(k - 16) = 1000n
(k + 16)(k - 16) = 1000n
Iggy Iguana
2012-03-17 20:15:43
subtract 256 and factor
subtract 256 and factor
professordad
2012-03-17 20:15:43
difference of squares?
difference of squares?
fmasroor
2012-03-17 20:15:43
256=16^2, so we have 1000n=(k-16)(k+16)
256=16^2, so we have 1000n=(k-16)(k+16)
DPatrick
2012-03-17 20:15:47
Good -- we can write as the difference of two perfect squares and factor.
Good -- we can write as the difference of two perfect squares and factor.
DPatrick
2012-03-17 20:16:08
How does this help?
How does this help?
professordad
2012-03-17 20:16:32
both k-16 and k+16 cannot be divisible by 125, so 125 divides either k-16 or k+16
both k-16 and k+16 cannot be divisible by 125, so 125 divides either k-16 or k+16
fireonice
2012-03-17 20:16:32
only one of the terms can contribute 125
only one of the terms can contribute 125
gomath888
2012-03-17 20:16:32
now just look where the 2s and 5s go
now just look where the 2s and 5s go
DPatrick
2012-03-17 20:16:45
Indeed, the right side must be a multiple of 1000.
Indeed, the right side must be a multiple of 1000.
DPatrick
2012-03-17 20:16:53
Only one of the factors can be a multiple of 5 (since the factors are 32 apart). Therefore one of the factors is a multiple of 125.
Only one of the factors can be a multiple of 5 (since the factors are 32 apart). Therefore one of the factors is a multiple of 125.
GeorgiaTechMan
2012-03-17 20:17:04
also, both k+16 and k-16 must be divisible by 4
also, both k+16 and k-16 must be divisible by 4
DPatrick
2012-03-17 20:17:33
Right. They clearly must both be even, but if one is not a multiple of 4, neither is the other (since they're 32 apart), and we can't then have the right side be a multiple of 8.
Right. They clearly must both be even, but if one is not a multiple of 4, neither is the other (since they're 32 apart), and we can't then have the right side be a multiple of 8.
somanywindows
2012-03-17 20:17:45
(k + 16) or (k - 16) has to be a multiple of 500
(k + 16) or (k - 16) has to be a multiple of 500
himym83
2012-03-17 20:17:45
thus must be divisible by 500
thus must be divisible by 500
DPatrick
2012-03-17 20:18:03
Right. One of the factors on the right side must be a multiple of 500.
Right. One of the factors on the right side must be a multiple of 500.
Relativity1618
2012-03-17 20:18:35
so now we list values for which either is true
so now we list values for which either is true
Iggy Iguana
2012-03-17 20:18:35
16, 500-16, 500 + 16, ...2500-16 is 10th
16, 500-16, 500 + 16, ...2500-16 is 10th
lucylai
2012-03-17 20:18:35
form a list of values for k
form a list of values for k
DPatrick
2012-03-17 20:18:44
Right. We can just make a list. The first 10 k's are 16, 500-16, 500+16, 1000-16, ..., up to the tenth one being 2500-16.
Right. We can just make a list. The first 10 k's are 16, 500-16, 500+16, 1000-16, ..., up to the tenth one being 2500-16.
DPatrick
2012-03-17 20:18:59
Don't simplify 2500-16, because it's easier to square as it is!
Don't simplify 2500-16, because it's easier to square as it is!
DPatrick
2012-03-17 20:19:12
Now what?
Now what?
AlcumusGuy
2012-03-17 20:19:36
look back at T
look back at T
himym83
2012-03-17 20:19:37
get rid of 256
get rid of 256
CantonMathGuy
2012-03-17 20:19:37
make it mod 1000
make it mod 1000
fireonice
2012-03-17 20:19:37
drop the 256 and divide 1000
drop the 256 and divide 1000
scgorantla
2012-03-17 20:19:37
subtract 256 and divide by 1000
subtract 256 and divide by 1000
DPatrick
2012-03-17 20:19:45
Right, we chop off the 256, and divide by 1000.
Right, we chop off the 256, and divide by 1000.
GeorgiaTechMan
2012-03-17 20:20:06
so our answer is 170!
so our answer is 170!
AkshajK
2012-03-17 20:20:06
Therefore, its 170
Therefore, its 170
himym83
2012-03-17 20:20:06
remainder is 170
remainder is 170
DPatrick
2012-03-17 20:20:45
I'm going to take a short break to rest my typing fingers before we tackle the final five. We'll resume at :25 past the hour (about 4 minutes from now). Go stretch your legs!
I'm going to take a short break to rest my typing fingers before we tackle the final five. We'll resume at :25 past the hour (about 4 minutes from now). Go stretch your legs!
DPatrick
2012-03-17 20:25:36
OK, we're back. The ceiling is still leaking here but rrusczyk is here to put more buckets underneath! :)
OK, we're back. The ceiling is still leaking here but rrusczyk is here to put more buckets underneath! :)
DPatrick
2012-03-17 20:26:09
(For what it's worth I thought this was the hardest problem.)
(For what it's worth I thought this was the hardest problem.)
DPatrick
2012-03-17 20:27:01
You can't make much headway unless you make a couple of key observations.
You can't make much headway unless you make a couple of key observations.
Iggy Iguana
2012-03-17 20:27:26
note that x+y is always divisible by 3 and x-y is always divisible by 5, so now all we have to do is prove all of these points can be hopped to
note that x+y is always divisible by 3 and x-y is always divisible by 5, so now all we have to do is prove all of these points can be hopped to
gomath888
2012-03-17 20:27:26
sum invariant mod 3, difference invariant mod 5
sum invariant mod 3, difference invariant mod 5
GeorgiaTechMan
2012-03-17 20:27:26
sum divisible by 3, difference divisible by 5
sum divisible by 3, difference divisible by 5
DPatrick
2012-03-17 20:27:41
Right. These are the key observations.
Right. These are the key observations.
DPatrick
2012-03-17 20:27:50
All of the coordinates add to a multiple of three. Therefore no matter where we travel, we will always be on a point with coordinates that add to a multiple of 3.
All of the coordinates add to a multiple of three. Therefore no matter where we travel, we will always be on a point with coordinates that add to a multiple of 3.
DPatrick
2012-03-17 20:28:08
And, the differences in the coordinates are always a multiple of five. Therefore no matter where we travel, we will always be on a point with coordinates that have difference equal to a multiple of 5.
And, the differences in the coordinates are always a multiple of five. Therefore no matter where we travel, we will always be on a point with coordinates that have difference equal to a multiple of 5.
DPatrick
2012-03-17 20:29:20
The question is, before we start counting: can we actually reach all such points?
The question is, before we start counting: can we actually reach all such points?
scgorantla
2012-03-17 20:29:55
yes
yes
somanywindows
2012-03-17 20:29:55
yes
yes
scgorantla
2012-03-17 20:29:55
yes, we can
yes, we can
GeorgiaTechMan
2012-03-17 20:29:55
yes
yes
DPatrick
2012-03-17 20:30:23
How do we know?
How do we know?
DPatrick
2012-03-17 20:31:09
Remember, we can only add these vectors above. We can’t subtract them. Therefore that might restrict the places we can go. (For example, even if we could move left some amount that doesn’t show us that we can move right that same amount.)
Remember, we can only add these vectors above. We can’t subtract them. Therefore that might restrict the places we can go. (For example, even if we could move left some amount that doesn’t show us that we can move right that same amount.)
Iggy Iguana
2012-03-17 20:32:05
you can make (0, 15)
you can make (0, 15)
CantonMathGuy
2012-03-17 20:32:06
5A + 5B + 9C + 9D = 0
5A + 5B + 9C + 9D = 0
DPatrick
2012-03-17 20:32:42
Indeed, we can track the points that we can move to horizontally and vertically, and we can also see that we can get back to 0.
Indeed, we can track the points that we can move to horizontally and vertically, and we can also see that we can get back to 0.
DPatrick
2012-03-17 20:33:39
There are a number of ways to show that you can reach every possible point. (It might also be reasonable, on the contest, to assume you can reach every possible point, and proceed with the counting.)
There are a number of ways to show that you can reach every possible point. (It might also be reasonable, on the contest, to assume you can reach every possible point, and proceed with the counting.)
DPatrick
2012-03-17 20:34:42
What I did is to show that you can move from a point (x,y) on x-y = 5l to a point (x,y) on either x-y = 5(l-1) or 5(l+1) by using either A or B. So we can hope between the lines of slope 1.
What I did is to show that you can move from a point (x,y) on x-y = 5l to a point (x,y) on either x-y = 5(l-1) or 5(l+1) by using either A or B. So we can hope between the lines of slope 1.
DPatrick
2012-03-17 20:35:46
We can then show that we can move along the lines of slope 1. For example, A+B = (9,9) and C+D = (-15,-15). So 2(A+B) + (C+D) = (3,3) and 3(A+B) + 2(C+D) = (-3,-3), and then we can hop up and down the line at will.
We can then show that we can move along the lines of slope 1. For example, A+B = (9,9) and C+D = (-15,-15). So 2(A+B) + (C+D) = (3,3) and 3(A+B) + 2(C+D) = (-3,-3), and then we can hop up and down the line at will.
DPatrick
2012-03-17 20:36:07
(And there are many other ways to show this too. It's rather tedious and boring.)
(And there are many other ways to show this too. It's rather tedious and boring.)
DPatrick
2012-03-17 20:36:35
So we can reach every lattice point (x,y) with x+y a multiple of 3 and x-y a multiple of 5.
So we can reach every lattice point (x,y) with x+y a multiple of 3 and x-y a multiple of 5.
DPatrick
2012-03-17 20:36:42
Now we are set to count. We want all of these points:
Now we are set to count. We want all of these points:
DPatrick
2012-03-17 20:36:49
Start counting. I’ll wait. . . .
Start counting. I’ll wait. . . .
Relativity1618
2012-03-17 20:37:06
there must be a better way!
there must be a better way!
DPatrick
2012-03-17 20:37:14
This is a square of dots, but it’s troublesome because the boundaries are at strange slopes and it’ll be very easy get off-by-one errors when counting each of these rows.
This is a square of dots, but it’s troublesome because the boundaries are at strange slopes and it’ll be very easy get off-by-one errors when counting each of these rows.
DPatrick
2012-03-17 20:37:27
Any better ideas?
Any better ideas?
fmasroor
2012-03-17 20:37:36
rotate it
rotate it
DPatrick
2012-03-17 20:37:40
:)
:)
DPatrick
2012-03-17 20:37:55
Technically what "rotate it" means is to use new coordinates.
Technically what "rotate it" means is to use new coordinates.
DPatrick
2012-03-17 20:38:23
This also makes the lattice conditions nicer: we need u to be a multiple of 3 and v to be a multiple of 5.
This also makes the lattice conditions nicer: we need u to be a multiple of 3 and v to be a multiple of 5.
Relativity1618
2012-03-17 20:38:45
a square
a square
AkshajK
2012-03-17 20:38:45
a square
a square
lucylai
2012-03-17 20:38:45
squares!!!
squares!!!
RelaxationUtopia
2012-03-17 20:38:45
square
square
DPatrick
2012-03-17 20:39:06
But there's one more condition in (u,v) land.
But there's one more condition in (u,v) land.
Iggy Iguana
2012-03-17 20:39:24
they must have same parity
they must have same parity
baldcypress
2012-03-17 20:39:29
u and v have the same parity
u and v have the same parity
DPatrick
2012-03-17 20:39:46
Right. Since our original x,y points were integers, we must have u and v be the same parity.
Right. Since our original x,y points were integers, we must have u and v be the same parity.
DPatrick
2012-03-17 20:39:56
They're either both even or both odd.
They're either both even or both odd.
DPatrick
2012-03-17 20:40:08
So we want to count solutions to:
So we want to count solutions to:
DPatrick
2012-03-17 20:40:34
Now for the counting.
Now for the counting.
hrithikguy
2012-03-17 20:40:43
clearly casework on whether they are both even or both odd
clearly casework on whether they are both even or both odd
GeorgiaTechMan
2012-03-17 20:40:43
we can do two cases; both are even or both are d=odd.
we can do two cases; both are even or both are d=odd.
DPatrick
2012-03-17 20:40:54
Sounds good.
Sounds good.
DPatrick
2012-03-17 20:41:05
If u is an even multiple of 3, then u is a multiple of 6. The multiples of 6 between -100 and 100 are -96,-90,...,90,96, and there are 33 of those.
If u is an even multiple of 3, then u is a multiple of 6. The multiples of 6 between -100 and 100 are -96,-90,...,90,96, and there are 33 of those.
DPatrick
2012-03-17 20:41:17
How many v's work?
How many v's work?
mcdonalds106_7
2012-03-17 20:41:41
21 vs
21 vs
aussiedoodle
2012-03-17 20:41:41
21
21
DPatrick
2012-03-17 20:41:45
If v is an even multiple of 5, then v is a multiple of 10. There are 21 multiples of 10 between -100 and 100 (inclusive).
If v is an even multiple of 5, then v is a multiple of 10. There are 21 multiples of 10 between -100 and 100 (inclusive).
DPatrick
2012-03-17 20:42:00
So there are 33*21 (u,v)'s in the u,v even case.
So there are 33*21 (u,v)'s in the u,v even case.
DPatrick
2012-03-17 20:42:10
How many odd (u,v)'s?
How many odd (u,v)'s?
mcdonalds106_7
2012-03-17 20:42:30
34*20
34*20
Bryan.C
2012-03-17 20:42:30
34*20
34*20
ProbaBillity
2012-03-17 20:42:30
34*20
34*20
DPatrick
2012-03-17 20:42:42
The odd multiples of 3 in the range are -99,-93,...,93,99. There are 34 of those.
The odd multiples of 3 in the range are -99,-93,...,93,99. There are 34 of those.
DPatrick
2012-03-17 20:42:54
The odd multiples of 5 in this range occur between the even values, so there is one fewer. There are 20 odd multiples of 5 in this region.
The odd multiples of 5 in this range occur between the even values, so there is one fewer. There are 20 odd multiples of 5 in this region.
DPatrick
2012-03-17 20:43:00
(-95, -85, ..., 85, 95)
(-95, -85, ..., 85, 95)
DPatrick
2012-03-17 20:43:11
So there are 34*20 (u,v)'s in the u,v odd case.
So there are 34*20 (u,v)'s in the u,v odd case.
professordad
2012-03-17 20:43:26
33*21 + 34*20 = 1373, so 373
33*21 + 34*20 = 1373, so 373
Iggy Iguana
2012-03-17 20:43:26
so we have 680+693=1373, for an answer of 373
so we have 680+693=1373, for an answer of 373
fractals
2012-03-17 20:43:26
So 1373 total, so the answer is 373.
So 1373 total, so the answer is 373.
DPatrick
2012-03-17 20:44:17
What's slightly bad about this problem from the point-of-view of a contest is that you don't have to prove that all the points are reachable -- you could assume it (and be right). And proving it is tedious.
What's slightly bad about this problem from the point-of-view of a contest is that you don't have to prove that all the points are reachable -- you could assume it (and be right). And proving it is tedious.
lucylai
2012-03-17 20:45:01
30 degree angles
30 degree angles
RelaxationUtopia
2012-03-17 20:45:01
30 degrees
30 degrees
ABCDE
2012-03-17 20:45:01
30 degree angles
30 degree angles
Iggy Iguana
2012-03-17 20:45:01
3 30 degree angles
3 30 degree angles
DPatrick
2012-03-17 20:45:04
We have 30 degree angles. We're also given DE/BE = 8/15, so we'll add that to the diagram, too:
We have 30 degree angles. We're also given DE/BE = 8/15, so we'll add that to the diagram, too:
thecmd999
2012-03-17 20:45:21
angle bisector theorem!
angle bisector theorem!
RelaxationUtopia
2012-03-17 20:45:21
diagram ---> angle bisector
diagram ---> angle bisector
Typhoon131
2012-03-17 20:45:21
Angle Bisector Theorem
Angle Bisector Theorem
DPatrick
2012-03-17 20:45:27
We have a ratio of sides and we have angle bisectors; we break out the Angle Bisector Theorem, which tells us that CD/CB = DE/BE. So, we have CD/CB = 8/15, and we add that to the diagram:
We have a ratio of sides and we have angle bisectors; we break out the Angle Bisector Theorem, which tells us that CD/CB = DE/BE. So, we have CD/CB = 8/15, and we add that to the diagram:
DPatrick
2012-03-17 20:45:59
Now, there are lots of ways to proceed via trig bashing. But there is a very quick, simple solution that just uses 30-60-90 triangles!
Now, there are lots of ways to proceed via trig bashing. But there is a very quick, simple solution that just uses 30-60-90 triangles!
scgorantla
2012-03-17 20:46:12
draw the height from D to BC
draw the height from D to BC
Typhoon131
2012-03-17 20:46:12
Drop perpendicular from D to BC
Drop perpendicular from D to BC
ABCDE
2012-03-17 20:46:12
Drop altitude from D to BC.
Drop altitude from D to BC.
DPatrick
2012-03-17 20:46:21
We build a 30-60-90 triangle involving a side we have information about by dropping an altitude from D:
We build a 30-60-90 triangle involving a side we have information about by dropping an altitude from D:
DPatrick
2012-03-17 20:46:37
Why did I bother doing that?
Why did I bother doing that?
Iggy Iguana
2012-03-17 20:46:47
we have YC = 4t and DY = 4sqrt3 t
we have YC = 4t and DY = 4sqrt3 t
Typhoon131
2012-03-17 20:47:12
CY = 4t, BY = 11t
CY = 4t, BY = 11t
Relativity1618
2012-03-17 20:47:12
BY=11T
BY=11T
Iggy Iguana
2012-03-17 20:47:21
so BY = 11t
so BY = 11t
scgorantla
2012-03-17 20:47:21
BY=11t
BY=11t
mathswimmer
2012-03-17 20:47:27
DY/YB
DY/YB
krmathcounts
2012-03-17 20:47:27
tan B = DY/YB
tan B = DY/YB
DPatrick
2012-03-17 20:47:30
And now we're done!
And now we're done!
DPatrick
2012-03-17 20:47:41
BY = BC - YC = 15t - 4t = 11t.
BY = BC - YC = 15t - 4t = 11t.
DPatrick
2012-03-17 20:48:03
And because we have our eye on the ball, we can immediately finish by computing tan B.
And because we have our eye on the ball, we can immediately finish by computing tan B.
mcdonalds106_7
2012-03-17 20:48:33
way easier than #11 wow
way easier than #11 wow
DPatrick
2012-03-17 20:48:40
I agree. Don't make problems harder than they are!
I agree. Don't make problems harder than they are!
ahaanomegas
2012-03-17 20:49:12
Diagram!
Diagram!
Relativity1618
2012-03-17 20:49:12
draw a diagram
draw a diagram
DPatrick
2012-03-17 20:49:16
In a construction problem, it is often best to start with the final diagram, and look for properties that will help us construct the diagram.
In a construction problem, it is often best to start with the final diagram, and look for properties that will help us construct the diagram.
DPatrick
2012-03-17 20:49:56
What is a key fact that we need to determine?
What is a key fact that we need to determine?
mcdonalds106_7
2012-03-17 20:50:14
draw center to vertices
draw center to vertices
theone142857
2012-03-17 20:50:14
Draw the center and connect it to P,Q,R
Draw the center and connect it to P,Q,R
fractals
2012-03-17 20:50:14
Where the center is.
Where the center is.
DPatrick
2012-03-17 20:50:41
Right. It looks like the center is inside the triangle. If you do an accurate enough sketch you'll convince yourself.
Right. It looks like the center is inside the triangle. If you do an accurate enough sketch you'll convince yourself.
RelaxationUtopia
2012-03-17 20:50:48
Wait how do I know what triangle would be the biggest?
Wait how do I know what triangle would be the biggest?
tc1729
2012-03-17 20:51:10
is there only one such equilateral triangle that can be constructed?
is there only one such equilateral triangle that can be constructed?
Iggy Iguana
2012-03-17 20:51:13
there's another really small triangle such that the center is outside triangle
there's another really small triangle such that the center is outside triangle
DPatrick
2012-03-17 20:51:28
These are good questions -- how do we know that this is essentially the only triangle that we want?
These are good questions -- how do we know that this is essentially the only triangle that we want?
DPatrick
2012-03-17 20:51:54
We can let R be any point on circle C_5. We then want to find the appropriate points P and Q.
We can let R be any point on circle C_5. We then want to find the appropriate points P and Q.
DPatrick
2012-03-17 20:52:08
What do we know about equilateral triangle PQR that may help us construct it?
What do we know about equilateral triangle PQR that may help us construct it?
Relativity1618
2012-03-17 20:52:22
60 degrees
60 degrees
mathswimmer
2012-03-17 20:52:22
60 degrees
60 degrees
Iggy Iguana
2012-03-17 20:52:22
equal sides
equal sides
scgorantla
2012-03-17 20:52:22
all angles are 60
all angles are 60
DPatrick
2012-03-17 20:52:42
In particular we know that <PRQ = 60. How can we find points P on circle C_3 and Q on circle C_4 so that <PRQ = 60?
In particular we know that <PRQ = 60. How can we find points P on circle C_3 and Q on circle C_4 so that <PRQ = 60?
scgorantla
2012-03-17 20:52:57
rotation?
rotation?
DPatrick
2012-03-17 20:53:03
We can rotate circle C_3 around point R by 60 degrees, to obtain circle C_3'.
We can rotate circle C_3 around point R by 60 degrees, to obtain circle C_3'.
DPatrick
2012-03-17 20:53:32
If P is on C_3, then P rotates around to Q, so Q must be on C_3'.
If P is on C_3, then P rotates around to Q, so Q must be on C_3'.
ProbaBillity
2012-03-17 20:53:36
the intersection of C3' and C4 is Q
the intersection of C3' and C4 is Q
DPatrick
2012-03-17 20:53:54
But Q is also on C_4. So there are only two possible locations for Q, and thus only 2 possible triangles to consider.
But Q is also on C_4. So there are only two possible locations for Q, and thus only 2 possible triangles to consider.
ProbaBillity
2012-03-17 20:53:58
the tiny equilateral triangle comes from the other intersection point
the tiny equilateral triangle comes from the other intersection point
DPatrick
2012-03-17 20:54:22
Right, there's a tiny triangle coming from the other intersection point, but it is clearly way way smaller.
Right, there's a tiny triangle coming from the other intersection point, but it is clearly way way smaller.
DPatrick
2012-03-17 20:54:33
So the triangle we started with in our diagram is definitely the one we want.
So the triangle we started with in our diagram is definitely the one we want.
DPatrick
2012-03-17 20:54:49
And if you brought a ruler and compass, you could actually try to draw a pretty accurate picture.
And if you brought a ruler and compass, you could actually try to draw a pretty accurate picture.
DPatrick
2012-03-17 20:55:03
And back to an earlier question: note that for this solution, the center of the circles O lies inside equilateral triangle PQR.
And back to an earlier question: note that for this solution, the center of the circles O lies inside equilateral triangle PQR.
DPatrick
2012-03-17 20:55:15
We know that OP = 3, OQ = 4, and OR = 5. Do these lengths suggest anything to you?
We know that OP = 3, OQ = 4, and OR = 5. Do these lengths suggest anything to you?
scgorantla
2012-03-17 20:55:25
I see a right triangle!
I see a right triangle!
Relativity1618
2012-03-17 20:55:25
pythag
pythag
himym83
2012-03-17 20:55:25
right triangles
right triangles
Iggy Iguana
2012-03-17 20:55:25
right trianlges!
right trianlges!
ProbaBillity
2012-03-17 20:55:25
look for right triangles
look for right triangles
henrypickle
2012-03-17 20:55:25
3-4-5 right triangle
3-4-5 right triangle
DPatrick
2012-03-17 20:55:36
The lengths 3, 4, and 5 form the sides of a right triangle. So it would be ideal if we can construct a triangle with these lengths in the diagram. Is there any way to do that?
The lengths 3, 4, and 5 form the sides of a right triangle. So it would be ideal if we can construct a triangle with these lengths in the diagram. Is there any way to do that?
dandan
2012-03-17 20:55:56
rotate it
rotate it
himym83
2012-03-17 20:55:57
rotation
rotation
mathswimmer
2012-03-17 20:55:57
some transformation?
some transformation?
mcdonalds106_7
2012-03-17 20:55:57
rotate the triangle a bunch of times
rotate the triangle a bunch of times
prezcoin
2012-03-17 20:55:57
rotation by 60deg to make that triangle appear
rotation by 60deg to make that triangle appear
DPatrick
2012-03-17 20:56:32
There are a lot of things you could do -- one good idea is to rotate the picture 60 degrees clockwise, centered at point P:
There are a lot of things you could do -- one good idea is to rotate the picture 60 degrees clockwise, centered at point P:
DPatrick
2012-03-17 20:56:59
So R gets rotated over to Q, and O gets rotated to a new point O'. (I've removed the circles for a little clarity)
So R gets rotated over to Q, and O gets rotated to a new point O'. (I've removed the circles for a little clarity)
Iggy Iguana
2012-03-17 20:57:12
OO'P is equalatera
OO'P is equalatera
DPatrick
2012-03-17 20:57:36
Right: OP = O'P because of the rotation, and also angle OPO' = 60 degrees because of the rotation. So OPO' is equilateral.
Right: OP = O'P because of the rotation, and also angle OPO' = 60 degrees because of the rotation. So OPO' is equilateral.
mcdonalds106_7
2012-03-17 20:57:56
we see that OO'Q is 3-4-5 as well
we see that OO'Q is 3-4-5 as well
letsruletheworldtogether
2012-03-17 20:57:56
QO' is 5
QO' is 5
DPatrick
2012-03-17 20:58:11
Right! RO rotates to QO', so the length RO is preserved, and QO' = 5.
Right! RO rotates to QO', so the length RO is preserved, and QO' = 5.
DPatrick
2012-03-17 20:58:26
This means that OO'Q is our 3-4-5 right triangle. How does that help us?
This means that OO'Q is our 3-4-5 right triangle. How does that help us?
baldcypress
2012-03-17 20:58:40
so < qop is 150
so < qop is 150
scgorantla
2012-03-17 20:58:41
Now we can just apply the law of cosines
Now we can just apply the law of cosines
DPatrick
2012-03-17 20:59:11
Right. We know angle QOO' is 90 (it's the right angle in our 3-4-5 triangle), and O'OP is 60 degrees, so QOP is a 150-degree angle.
Right. We know angle QOO' is 90 (it's the right angle in our 3-4-5 triangle), and O'OP is 60 degrees, so QOP is a 150-degree angle.
DPatrick
2012-03-17 20:59:37
So we can use the Law of Cosines on the triangle QOP to compute the length QP, which is the side of the triangle PQR that we care about in the problem!
So we can use the Law of Cosines on the triangle QOP to compute the length QP, which is the side of the triangle PQR that we care about in the problem!
FalconPower
2012-03-17 21:00:02
Qp^2=4^2+3^2-2*4*3*cos150
Qp^2=4^2+3^2-2*4*3*cos150
tc1729
2012-03-17 21:00:06
QP^2 = 3^2+4^2-2(12)cos 150
QP^2 = 3^2+4^2-2(12)cos 150
superpi83
2012-03-17 21:00:49
Then use area=s^2*sqrt(3)/4
Then use area=s^2*sqrt(3)/4
Relativity1618
2012-03-17 21:00:49
now we can find the area
now we can find the area
Iggy Iguana
2012-03-17 21:00:49
so now just multiply by sqrt3 / 4 to get area
so now just multiply by sqrt3 / 4 to get area
fractals
2012-03-17 21:00:49
And the area is PQ^2sqrt3/4
And the area is PQ^2sqrt3/4
letsruletheworldtogether
2012-03-17 21:00:49
times sqrt(3)/4
times sqrt(3)/4
theone142857
2012-03-17 21:00:49
multiply by sqrt{3}/4
multiply by sqrt{3}/4
himym83
2012-03-17 21:00:49
multiply by sqrt3/4 to get ans
multiply by sqrt3/4 to get ans
theone142857
2012-03-17 21:01:13
So since 25+9+4+3=41. So 041 is our answer.
So since 25+9+4+3=41. So 041 is our answer.
Relativity1618
2012-03-17 21:01:14
9+25+4+3=41
9+25+4+3=41
fractals
2012-03-17 21:01:26
Reflecting O over PQ, QR, and RP and making a hexagon, and drawing O'O''O''' works as well.
Reflecting O over PQ, QR, and RP and making a hexagon, and drawing O'O''O''' works as well.
DPatrick
2012-03-17 21:01:47
Certainly there are other transformations that work -- the key is doing something that produces a 3-4-5 triangle, and thus a right angle.
Certainly there are other transformations that work -- the key is doing something that produces a 3-4-5 triangle, and thus a right angle.
DPatrick
2012-03-17 21:01:59
Also, this problem can be solved very carefully by using coordinates -- the trick is to fix the coordinates of the the points (using the fact that the triangle is equilateral), and solve for the center.
Also, this problem can be solved very carefully by using coordinates -- the trick is to fix the coordinates of the the points (using the fact that the triangle is equilateral), and solve for the center.
DPatrick
2012-03-17 21:02:39
What information do we get from the cubic?
What information do we get from the cubic?
thecmd999
2012-03-17 21:02:53
vieta! a+b+c=0
vieta! a+b+c=0
fireonice
2012-03-17 21:02:53
a+b+c=0 from Vieta
a+b+c=0 from Vieta
lucylai
2012-03-17 21:02:53
a+b+c=0
a+b+c=0
Yongyi781
2012-03-17 21:02:53
a+b+c = 0
a+b+c = 0
scgorantla
2012-03-17 21:02:53
sum of roots is 0
sum of roots is 0
professordad
2012-03-17 21:02:53
the sum of a,b,c is 0
the sum of a,b,c is 0
DPatrick
2012-03-17 21:03:23
We can throw the cubic away now -- it can't possibly tell us anything else.
We can throw the cubic away now -- it can't possibly tell us anything else.
DPatrick
2012-03-17 21:04:05
Now this problem had the unfortunate feature that you could make simplifying assumptions about the roots, and everything would work out nicely. But I want to show how to solve the problem without making any such assumptions.
Now this problem had the unfortunate feature that you could make simplifying assumptions about the roots, and everything would work out nicely. But I want to show how to solve the problem without making any such assumptions.
Relativity1618
2012-03-17 21:04:14
plot the roots?
plot the roots?
DPatrick
2012-03-17 21:04:22
Let's suppose (without loss of generality) that c is the right angle, and that a rotates counterclockwise about c to get to b, like so:
Let's suppose (without loss of generality) that c is the right angle, and that a rotates counterclockwise about c to get to b, like so:
DPatrick
2012-03-17 21:04:54
What is rotation by 90 degrees in the complex plane equivalent to?
What is rotation by 90 degrees in the complex plane equivalent to?
Relativity1618
2012-03-17 21:05:11
multiplying by i
multiplying by i
osmosis92
2012-03-17 21:05:11
times i
times i
gomath888
2012-03-17 21:05:11
multiplication by i
multiplication by i
djmathman
2012-03-17 21:05:11
Multiplying by i
Multiplying by i
mathswimmer
2012-03-17 21:05:11
multiply by i
multiply by i
superpi83
2012-03-17 21:05:11
multiplication by i
multiplication by i
DPatrick
2012-03-17 21:05:20
It's multiplication by i. And possibly scaling by a positive real number.
It's multiplication by i. And possibly scaling by a positive real number.
DPatrick
2012-03-17 21:06:01
Now what?
Now what?
coldsummer
2012-03-17 21:06:21
simplifying and substitution?
simplifying and substitution?
DPatrick
2012-03-17 21:07:01
How does this help. How do we "solve" this?
How does this help. How do we "solve" this?
scgorantla
2012-03-17 21:07:20
ratio of a to b
ratio of a to b
calculus17
2012-03-17 21:07:24
A IN TERMS OF B
A IN TERMS OF B
DPatrick
2012-03-17 21:07:31
Right, it fixes the ratio of a to b.
Right, it fixes the ratio of a to b.
haihongjin
2012-03-17 21:07:46
r was used in the proplem
r was used in the proplem
DPatrick
2012-03-17 21:08:03
oops...good point. The r I'm using here is not the same r that's in the cubic in the problem. My bad.
oops...good point. The r I'm using here is not the same r that's in the cubic in the problem. My bad.
fmasroor
2012-03-17 21:08:15
|a|^2+...=250
|a|^2+...=250
capu
2012-03-17 21:08:15
well remember that the squares add up to 250
well remember that the squares add up to 250
DPatrick
2012-03-17 21:08:30
Now we use the remaining bit of data: the sum of the squares of the magnitudes is 250.
Now we use the remaining bit of data: the sum of the squares of the magnitudes is 250.
DPatrick
2012-03-17 21:09:16
Well, that may look messy, but keep your eye on the ball! What are we trying to find?
Well, that may look messy, but keep your eye on the ball! What are we trying to find?
Iggy Iguana
2012-03-17 21:09:27
hypotenuse
hypotenuse
Relativity1618
2012-03-17 21:09:27
h^2
h^2
proglote
2012-03-17 21:09:35
(a-b)^2
(a-b)^2
somanywindows
2012-03-17 21:09:39
distance from a to b
distance from a to b
djmathman
2012-03-17 21:10:03
Multiply by 3/2!
Multiply by 3/2!
DPatrick
2012-03-17 21:10:06
This is exactly 3/2 times the quantity of 250 from our previous calculation!
This is exactly 3/2 times the quantity of 250 from our previous calculation!
CantonMathGuy
2012-03-17 21:10:21
375
375
ProbaBillity
2012-03-17 21:10:22
375
375
FalconPower
2012-03-17 21:10:22
375!!!
375!!!
DPatrick
2012-03-17 21:10:47
There are some shortcuts to this problem. You could assume that the triangle is isosceles (that is, that r=1 in the above computation) and it'd still work. But my computation actually proves that it works for all a,b,c satisfying the conditions of the problem.
There are some shortcuts to this problem. You could assume that the triangle is isosceles (that is, that r=1 in the above computation) and it'd still work. But my computation actually proves that it works for all a,b,c satisfying the conditions of the problem.
DPatrick
2012-03-17 21:11:27
My colleague Jeremy Copeland pointed out that he assumed the triangle was degenerate, that is that b=c, and it still works with much simpler computation.
My colleague Jeremy Copeland pointed out that he assumed the triangle was degenerate, that is that b=c, and it still works with much simpler computation.
DPatrick
2012-03-17 21:11:39
And last but not least,
And last but not least,
DPatrick
2012-03-17 21:12:04
Yikes. How can we begin to break this down?
Yikes. How can we begin to break this down?
Relativity1618
2012-03-17 21:12:16
mods?
mods?
fractals
2012-03-17 21:12:16
Modular Arithmetic!
Modular Arithmetic!
DPatrick
2012-03-17 21:12:52
We're almost certainly going to want to work mod n, since we only care about how far about things are around the circle, which means looking at the differences mod n.
We're almost certainly going to want to work mod n, since we only care about how far about things are around the circle, which means looking at the differences mod n.
DPatrick
2012-03-17 21:13:01
What does condition (1) tell us?
What does condition (1) tell us?
scgorantla
2012-03-17 21:13:27
multiply the seat you were in by a
multiply the seat you were in by a
fractals
2012-03-17 21:13:27
a is relatively prime to n
a is relatively prime to n
DPatrick
2012-03-17 21:13:52
Right. The reseating operation is taking everyone's seat and multiplying it by a, then taking mod n to figure out where they sit.
Right. The reseating operation is taking everyone's seat and multiplying it by a, then taking mod n to figure out where they sit.
DPatrick
2012-03-17 21:14:07
But everybody has to have their own seat after this is all done!
But everybody has to have their own seat after this is all done!
DPatrick
2012-03-17 21:14:36
(Otherwise two of them will end up in the same seat after multiplying by a.)
(Otherwise two of them will end up in the same seat after multiplying by a.)
turak
2012-03-17 21:14:51
a is not a zero divisor mod n
a is not a zero divisor mod n
ahaanomegas
2012-03-17 21:14:52
(a, n) = 1.
(a, n) = 1.
scgorantla
2012-03-17 21:14:52
so a is relatively prime to n!
so a is relatively prime to n!
DPatrick
2012-03-17 21:15:35
(For example, if n = 14 and a = 10, then j-k = 7 fails, since (j-k)a = 10*7 = 70 is a multiple of 14.)
(For example, if n = 14 and a = 10, then j-k = 7 fails, since (j-k)a = 10*7 = 70 is a multiple of 14.)
Relativity1618
2012-03-17 21:15:51
introduce statement 2
introduce statement 2
DPatrick
2012-03-17 21:15:55
What about condition (2)? What can we say about it?
What about condition (2)? What can we say about it?
karatemagic7
2012-03-17 21:16:38
gcd(a-1,n)=1 and gcd(a+1,n)=1
gcd(a-1,n)=1 and gcd(a+1,n)=1
turak
2012-03-17 21:16:38
neither a-1 nor a+1 are zero divisors mod n
neither a-1 nor a+1 are zero divisors mod n
DPatrick
2012-03-17 21:16:56
That's true, but that skips a couple of steps we need to get there. Let me fill in the missing steps.
That's true, but that skips a couple of steps we need to get there. Let me fill in the missing steps.
DPatrick
2012-03-17 21:17:27
(That is, the difference between seats ak and aj is not the same as the difference from k to j in one direction)
(That is, the difference between seats ak and aj is not the same as the difference from k to j in one direction)
Iggy Iguana
2012-03-17 21:18:31
by same logic as before
by same logic as before
DPatrick
2012-03-17 21:19:20
What does this imply about n?
What does this imply about n?
Iggy Iguana
2012-03-17 21:19:36
so that means that 2 or 3 does not divide n because one of a-1, a, a+1 is divisible by 2, and one is divisible by 3
so that means that 2 or 3 does not divide n because one of a-1, a, a+1 is divisible by 2, and one is divisible by 3
baldcypress
2012-03-17 21:19:36
well then a can't have a factor of 2 or 3
well then a can't have a factor of 2 or 3
mcdonalds106_7
2012-03-17 21:19:36
so n cannot have a factor of 2 or 3
so n cannot have a factor of 2 or 3
guilt
2012-03-17 21:19:36
not divisible by 2, 3
not divisible by 2, 3
DPatrick
2012-03-17 21:19:56
Right. We can't have n even, since one of a-1, a, and a+1 must be even, and thus would have the factor of 2 in common with n.
Right. We can't have n even, since one of a-1, a, and a+1 must be even, and thus would have the factor of 2 in common with n.
DPatrick
2012-03-17 21:20:30
In a similar way, one of a-1, a, and a+1 must be a multiple of 3, and thus n can't be a multiple of 3 (because it'd have a factor of 3 in common with one of a-1, a, or a+1).
In a similar way, one of a-1, a, and a+1 must be a multiple of 3, and thus n can't be a multiple of 3 (because it'd have a factor of 3 in common with one of a-1, a, or a+1).
DPatrick
2012-03-17 21:20:40
So n cannot be a multiple of 2 or 3. Any other conditions?
So n cannot be a multiple of 2 or 3. Any other conditions?
scgorantla
2012-03-17 21:20:58
nope, thats it
nope, thats it
ProbaBillity
2012-03-17 21:20:58
no
no
superpi83
2012-03-17 21:21:01
nope, no other conditions if a=2
nope, no other conditions if a=2
DPatrick
2012-03-17 21:21:19
That's actually sufficient too. If n>1 is not a multiple of 2 or 3, then we can pick a = 2 and everything works, since neither 1, 2, nor 3 would have a common factor with n.
That's actually sufficient too. If n>1 is not a multiple of 2 or 3, then we can pick a = 2 and everything works, since neither 1, 2, nor 3 would have a common factor with n.
DPatrick
2012-03-17 21:21:31
So to finish the problem, we need to count all the n with 1 < n < 1000 such that n is not a multiple of 2 or 3.
So to finish the problem, we need to count all the n with 1 < n < 1000 such that n is not a multiple of 2 or 3.
Iggy Iguana
2012-03-17 21:21:41
n has to be 1 or 5 mod 6
n has to be 1 or 5 mod 6
DPatrick
2012-03-17 21:21:49
Yes: an easy way is to recognize that this means that n must be 1 or 5 (mod 6).
Yes: an easy way is to recognize that this means that n must be 1 or 5 (mod 6).
DPatrick
2012-03-17 21:21:54
So for every 6k (that is, every multiple of 6) between 1 and 1000, the numbers 6k-1 and 6k+1 will both work.
So for every 6k (that is, every multiple of 6) between 1 and 1000, the numbers 6k-1 and 6k+1 will both work.
ProbaBillity
2012-03-17 21:22:12
166*2 = 332
166*2 = 332
mcdonalds106_7
2012-03-17 21:22:14
so our answer is 166*2=332
so our answer is 166*2=332
DPatrick
2012-03-17 21:22:20
The smallest multiple is 6 and the largest is 996 = 6*166, so there are 166 valid multiples.
The smallest multiple is 6 and the largest is 996 = 6*166, so there are 166 valid multiples.
DPatrick
2012-03-17 21:23:05
(What's potentially sad about #15, of course, is that you could do all the hard number theory work, and then mess up the counting at the end. That's why it's important to be careful with the endgame to an AIME problem!)
(What's potentially sad about #15, of course, is that you could do all the hard number theory work, and then mess up the counting at the end. That's why it's important to be careful with the endgame to an AIME problem!)
DPatrick
2012-03-17 21:23:15
That's it! That's for hanging out with me on a Saturday night.
That's it! That's for hanging out with me on a Saturday night.
DPatrick
2012-03-17 21:23:22
And please join us again for the AIME II Math Jam on Friday, March 30, when we'll do all this again for the AIME II.
And please join us again for the AIME II Math Jam on Friday, March 30, when we'll do all this again for the AIME II.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.