2012 AIME II Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2012 AIME 2.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Jeremy Copeland
copeland
2012-03-30 19:01:15
Welcome to the 2012 AIME II Math Jam!
Welcome to the 2012 AIME II Math Jam!
copeland
2012-03-30 19:01:20
I'm Jeremy Copeland, and I'll be leading our discussion tonight.
I'm Jeremy Copeland, and I'll be leading our discussion tonight.
copeland
2012-03-30 19:01:26
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
copeland
2012-03-30 19:01:35
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
copeland
2012-03-30 19:01:41
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
copeland
2012-03-30 19:01:51
There are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
copeland
2012-03-30 19:02:04
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
copeland
2012-03-30 19:02:21
We do have two teaching assistants with us tonight to help answer your questions: Carl Lian (CatalystOfNostalgia) and Kevin Hu (Aryth).
We do have two teaching assistants with us tonight to help answer your questions: Carl Lian (CatalystOfNostalgia) and Kevin Hu (Aryth).
copeland
2012-03-30 19:02:28
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
copeland
2012-03-30 19:02:46
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
copeland
2012-03-30 19:03:06
At a couple points during the Math Jam, I might get thirsty or hungry, or my fingers will get tired, and I'll take a 1-2 minute break. Other than that, we will simply plow through all 15 problems.
At a couple points during the Math Jam, I might get thirsty or hungry, or my fingers will get tired, and I'll take a 1-2 minute break. Other than that, we will simply plow through all 15 problems.
Navigator
2012-03-30 19:03:18
oh good! copeland!
oh good! copeland!

copeland
2012-03-30 19:03:20
I think the same thing every morning when I wake up!
I think the same thing every morning when I wake up!
DaChickenInc
2012-03-30 19:03:26


copeland
2012-03-30 19:03:28
I only rarely think that.
I only rarely think that.
copeland
2012-03-30 19:03:36
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test.
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test.
copeland
2012-03-30 19:03:47
That's not a question.
That's not a question.
copeland
2012-03-30 19:03:49
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test?
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test?
mathswimmer
2012-03-30 19:04:28
6
6
ABCDE
2012-03-30 19:04:28
14
14
alex31415
2012-03-30 19:04:28
#10! It was SOOOOOOOO easy!!!
#10! It was SOOOOOOOO easy!!!
EuclidGenius
2012-03-30 19:04:28
#16
#16
MNL9082
2012-03-30 19:04:28
number 5: it was way too easy and made me feel smart :)
number 5: it was way too easy and made me feel smart :)
nackster12
2012-03-30 19:04:28
13
13
kmc927
2012-03-30 19:04:28
#1
#1
ABCDE
2012-03-30 19:04:28
14
14
awesomemathlete
2012-03-30 19:04:28
10
10
googol.plex
2012-03-30 19:04:28
I liked number 3
I liked number 3
deepankar
2012-03-30 19:04:28
#9
#9
zinko1991
2012-03-30 19:04:28
#2
#2
ptea
2012-03-30 19:04:28
14. So simple, yet difficult.
14. So simple, yet difficult.
Voytek
2012-03-30 19:04:28
2 - Geometric series!
2 - Geometric series!
awesomemathlete
2012-03-30 19:04:28
number 10
number 10
lucylai
2012-03-30 19:04:28
7
7
Imsacred
2012-03-30 19:04:28
number 14
number 14
AndroidFusion
2012-03-30 19:04:28
13 because it was easy once you drew the diagram
13 because it was easy once you drew the diagram
centralbs
2012-03-30 19:04:28
12
12
lucylai
2012-03-30 19:04:28
7!!
7!!
kmc927
2012-03-30 19:04:28
and #5
and #5
awesomemathlete
2012-03-30 19:04:28
numer 10, it was easy, but elegant
numer 10, it was easy, but elegant
natec
2012-03-30 19:04:28
The one with the money exchange between students
The one with the money exchange between students
numbertheorist17
2012-03-30 19:04:28
14
14
shreyash
2012-03-30 19:04:28
12
12
va2010
2012-03-30 19:04:28
#8, YAY
#8, YAY
ahaanomegas
2012-03-30 19:04:28
Hardest: #15
Hardest: #15
copeland
2012-03-30 19:04:42
And many of you voted for 14:
And many of you voted for 14:
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
numbertheorist17
2012-03-30 19:04:43
14
14
copeland
2012-03-30 19:04:55
Early and often, right?
Early and often, right?
MNL9082
2012-03-30 19:05:01
seems fishy too me
seems fishy too me
copeland
2012-03-30 19:05:03
Let's get started.
Let's get started.
copeland
2012-03-30 19:05:07
1. Find the number of ordered pairs of positive integer solutions $(m,n)$ to the equation
\[20m + 12n = 2012.\]
1. Find the number of ordered pairs of positive integer solutions $(m,n)$ to the equation
\[20m + 12n = 2012.\]
copeland
2012-03-30 19:05:16
(Note that I'll always put the current problem statement up at the top of the window. You can resize the region at the top of the window by dragging the gray horizontal bar.)
(Note that I'll always put the current problem statement up at the top of the window. You can resize the region at the top of the window by dragging the gray horizontal bar.)
copeland
2012-03-30 19:05:22
See anything right off the bat?
See anything right off the bat?
lazorpenguin27143
2012-03-30 19:05:41
divide the equation by 4
divide the equation by 4
theone142857
2012-03-30 19:05:41
divide by 4
divide by 4
pleekey
2012-03-30 19:05:41
div by 4 first
div by 4 first
Hydroxide
2012-03-30 19:05:41
divide both sides by 4
divide both sides by 4
Flamewire
2012-03-30 19:05:41
Divide by 4
Divide by 4
admin25
2012-03-30 19:05:41
divide by 4
divide by 4
himym83
2012-03-30 19:05:41
divide by 4
divide by 4
pleekey
2012-03-30 19:05:41
everything divisible by 4
everything divisible by 4
joshxiong
2012-03-30 19:05:41
Divide both sides by 4.
Divide both sides by 4.
robinpark
2012-03-30 19:05:41
All coefficients are divisible by 4.
All coefficients are divisible by 4.
ahaanomegas
2012-03-30 19:05:41
We can divide each side of the equation by 4 to get: 5m + 3n = 503.
We can divide each side of the equation by 4 to get: 5m + 3n = 503.
copeland
2012-03-30 19:05:46
All of the numbers are divisible by 4, so the solutions to this equation are exactly the solutions to \[5m+3n=503.\]
All of the numbers are divisible by 4, so the solutions to this equation are exactly the solutions to \[5m+3n=503.\]
copeland
2012-03-30 19:05:49
What are the positive integer solutions to this equation?
What are the positive integer solutions to this equation?
AndroidFusion
2012-03-30 19:06:42
start with (100, 1)
start with (100, 1)
shreyash
2012-03-30 19:06:42
100,1
100,1
googol.plex
2012-03-30 19:06:42
the most obvious one is m=100, n=1
the most obvious one is m=100, n=1
vic317yeh
2012-03-30 19:06:42
100,1
100,1
PERFECTION
2012-03-30 19:06:42
first, if we maximize the value of m, we have (100,1)
first, if we maximize the value of m, we have (100,1)
ptea
2012-03-30 19:06:42
well (100, 1) is kind of a freebie.
well (100, 1) is kind of a freebie.
copeland
2012-03-30 19:06:47
We can start with the easiest solution, $5\cdot100+3\cdot1=503.$ This has to be the solution with smallest value for $n$.
We can start with the easiest solution, $5\cdot100+3\cdot1=503.$ This has to be the solution with smallest value for $n$.
lucylai
2012-03-30 19:07:13
(100, 1), (97, 6), ... (1, 166)
(100, 1), (97, 6), ... (1, 166)
alex31415
2012-03-30 19:07:13
(100,1), (97,6),...,(1,166)
(100,1), (97,6),...,(1,166)
centralbs
2012-03-30 19:07:13
n=1, 6, ... 166
n=1, 6, ... 166
Hydroxide
2012-03-30 19:07:13
m=100, 97, ..., 1 and the corresponding n
m=100, 97, ..., 1 and the corresponding n
ahaanomegas
2012-03-30 19:07:13
(m, n) = (100, 1) is a solution and we see that all positive n with units digit of 1 and 6 work. To keep m positive, n goes up to 166. So, the n that work are 1, 6, 11, 16, ..., 166.
(m, n) = (100, 1) is a solution and we see that all positive n with units digit of 1 and 6 work. To keep m positive, n goes up to 166. So, the n that work are 1, 6, 11, 16, ..., 166.
shreyash
2012-03-30 19:07:13
100 - 3k, 1 + 5k for k from 0 to 33
100 - 3k, 1 + 5k for k from 0 to 33
va2010
2012-03-30 19:07:13
100, 1 97, 6 I really see a pattern all
100, 1 97, 6 I really see a pattern all
Hydroxide
2012-03-30 19:07:13
keep going down by 3
keep going down by 3
Flamewire
2012-03-30 19:07:13
Decrement m by 3
Decrement m by 3
pleekey
2012-03-30 19:07:13
every time m goes down three, n goes up five
every time m goes down three, n goes up five
copeland
2012-03-30 19:07:17
From here, every time we increase $n$ we increase $5m+3n$ by a multiple of 3. Therefore to get to another solution we need to decrease $5m$ by a multiple of 3 as well.
From here, every time we increase $n$ we increase $5m+3n$ by a multiple of 3. Therefore to get to another solution we need to decrease $5m$ by a multiple of 3 as well.
copeland
2012-03-30 19:07:20
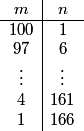
Therefore we must always decrease $m$ by some multiple of 3 to get from $(100,1)$ to another solution. Furthermore, subtracting 3 from $m$ and adding 5 to $n$ will always give us another solution. All solutions are below:
Therefore we must always decrease $m$ by some multiple of 3 to get from $(100,1)$ to another solution. Furthermore, subtracting 3 from $m$ and adding 5 to $n$ will always give us another solution. All solutions are below:
copeland
2012-03-30 19:07:30

copeland
2012-03-30 19:07:31
How many pairs are on that list?
How many pairs are on that list?
ahaanomegas
2012-03-30 19:07:57
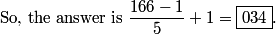
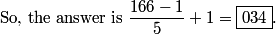
mjseaman1
2012-03-30 19:07:57
(1, 100) , (6, 97) ..... (165, 1) are the solutions. There are 34 in all.
(1, 100) , (6, 97) ..... (165, 1) are the solutions. There are 34 in all.
alex31415
2012-03-30 19:07:57
34
34
MNL9082
2012-03-30 19:07:57
34
34
claudiafeng
2012-03-30 19:07:57
34
34
ABCDE
2012-03-30 19:07:57
034
034
Seedleaf
2012-03-30 19:07:57
34 pairs! so 034
34 pairs! so 034
silvernight
2012-03-30 19:07:57
34
34
Flamewire
2012-03-30 19:07:57
99/3 = 33 + 1 = 34
99/3 = 33 + 1 = 34
shreyash
2012-03-30 19:07:57
34!
34!
ashgabat
2012-03-30 19:07:57
34 pairs.
34 pairs.
kangchangood
2012-03-30 19:07:57
34
34
sonchecky
2012-03-30 19:07:57
34
34
copeland
2012-03-30 19:08:00
We can count the number of copies of $m$: The list $1,4,7,10,\ldots,97,100$ has the same number of elements as the list we get by adding 2. Therefore we can count the number of elements on the list $3,6,9,12,\ldots,99,102$.
We can count the number of copies of $m$: The list $1,4,7,10,\ldots,97,100$ has the same number of elements as the list we get by adding 2. Therefore we can count the number of elements on the list $3,6,9,12,\ldots,99,102$.
copeland
2012-03-30 19:08:06
If we divide all the terms on this list by 3 we get the list $1,2,3,4,\ldots34$. There are $\boxed{034}$ solutions to our equation.
If we divide all the terms on this list by 3 we get the list $1,2,3,4,\ldots34$. There are $\boxed{034}$ solutions to our equation.
copeland
2012-03-30 19:08:32
Alrighty! Now we're rolling.
Alrighty! Now we're rolling.
copeland
2012-03-30 19:08:33
More math!
More math!
copeland
2012-03-30 19:09:01
2. Two geometric sequences $a_1$, $a_2$, $a_3, \dots$ and $b_1$, $b_2$, $b_3, \dots $ have the same common ratio, with $a_1 = 27$, $b_1 = 99$, and $a_{15} = b_{11}$. Find $a_9$.
2. Two geometric sequences $a_1$, $a_2$, $a_3, \dots$ and $b_1$, $b_2$, $b_3, \dots $ have the same common ratio, with $a_1 = 27$, $b_1 = 99$, and $a_{15} = b_{11}$. Find $a_9$.
copeland
2012-03-30 19:09:17
Formula time. What's the formula for the terms of a geometric sequence?
Formula time. What's the formula for the terms of a geometric sequence?
lazorpenguin27143
2012-03-30 19:09:58
by definition of geometric sequences write each term as a, ar, ar^2, etc
by definition of geometric sequences write each term as a, ar, ar^2, etc
shreyash
2012-03-30 19:09:58
a * r^(n-1)
a * r^(n-1)
Voytek
2012-03-30 19:09:58
an=a1*r^n-1
an=a1*r^n-1
tc1729
2012-03-30 19:09:58
a(1-r^n)/(1-r)
a(1-r^n)/(1-r)
zinko1991
2012-03-30 19:09:58
a, ar, ar^2, ar^3, ...
a, ar, ar^2, ar^3, ...
deepankar
2012-03-30 19:09:58
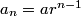
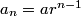
Seedleaf
2012-03-30 19:09:58
a, ar, ar^2, ar^3....... when a is starting term and r is the ratio
a, ar, ar^2, ar^3....... when a is starting term and r is the ratio
pl210741
2012-03-30 19:09:58
$a_n=(First term)(Common ration)^{n-1}$
$a_n=(First term)(Common ration)^{n-1}$
copeland
2012-03-30 19:10:09
We have two suggestions. I don't like using the -1, personally.
We have two suggestions. I don't like using the -1, personally.
copeland
2012-03-30 19:10:19
(And I'm in charge, so. . . .)
(And I'm in charge, so. . . .)
copeland
2012-03-30 19:10:21
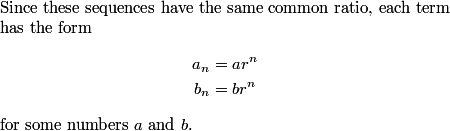
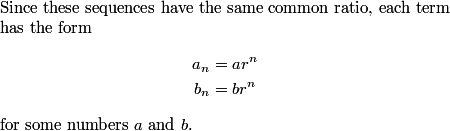
copeland
2012-03-30 19:10:27
How can we use the constraints $a_1=27$ and $b_1=99$?
How can we use the constraints $a_1=27$ and $b_1=99$?
Seedleaf
2012-03-30 19:12:14
27 and 99 can be the starting terms
27 and 99 can be the starting terms
kangchangood
2012-03-30 19:12:14
simply plug in 1 for n
simply plug in 1 for n
sonchecky
2012-03-30 19:12:14
$a/b=a_1/b_1=27/99=3/11$
$a/b=a_1/b_1=27/99=3/11$
lily6481
2012-03-30 19:12:14
plug in values
plug in values
Voytek
2012-03-30 19:12:14
27=ar and 99=br
27=ar and 99=br
shreyash
2012-03-30 19:12:14
a1 = a * r
a1 = a * r
shreyash
2012-03-30 19:12:14
b1 = b * r
b1 = b * r
theone142857
2012-03-30 19:12:14
get a and b in terms of r
get a and b in terms of r
AbsoluteFriend
2012-03-30 19:12:14
I think 27/r=a and 99/r=b
I think 27/r=a and 99/r=b
copeland
2012-03-30 19:12:24
My reflex is to divide these we get \[\frac{27}{99}=\frac{ar^1}{br^1}=\frac ab.\]
My reflex is to divide these we get \[\frac{27}{99}=\frac{ar^1}{br^1}=\frac ab.\]
copeland
2012-03-30 19:12:27
So we have:
So we have:
copeland
2012-03-30 19:12:30
$\frac3{11}=\frac ab$.
$\frac3{11}=\frac ab$.
copeland
2012-03-30 19:12:37
Now how do we use $a_{15}=b_{11}$?
Now how do we use $a_{15}=b_{11}$?
ahaanomegas
2012-03-30 19:13:25
So: r^4 = 11/3.
So: r^4 = 11/3.
nmandi7
2012-03-30 19:13:25
r^4 = 99/27
r^4 = 99/27
nmandi7
2012-03-30 19:13:25
a(r^4) = b
a(r^4) = b
googol.plex
2012-03-30 19:13:25
3/11*r^4=1
3/11*r^4=1
lucylai
2012-03-30 19:13:25
r^4=11/3
r^4=11/3
Imsacred
2012-03-30 19:13:25
since a15 = b11, a5 = b1
since a15 = b11, a5 = b1
admin25
2012-03-30 19:13:25
substitute n=15 into the equation for 'a' and n=11 into the equation for 'b'
substitute n=15 into the equation for 'a' and n=11 into the equation for 'b'
ahaanomegas
2012-03-30 19:13:25
Set the formulas for a_15 and b_11 equal using the expressions in terms of r. Then, we solve for r^4.
Set the formulas for a_15 and b_11 equal using the expressions in terms of r. Then, we solve for r^4.
va2010
2012-03-30 19:13:31
a(r^15)=b(r^11)
a(r^15)=b(r^11)
copeland
2012-03-30 19:13:32
We divide them again. If two numbers are equal, then their ratio is 1, so \[1=\frac{a_{15}}{b_{11}}=\frac{ar^{15}}{br^{11}}=\frac abr^4.\]
We divide them again. If two numbers are equal, then their ratio is 1, so \[1=\frac{a_{15}}{b_{11}}=\frac{ar^{15}}{br^{11}}=\frac abr^4.\]
copeland
2012-03-30 19:13:36
\[r^4=\frac ba=\frac{11}{3}.\]
\[r^4=\frac ba=\frac{11}{3}.\]
copeland
2012-03-30 19:13:38
And what is $a_9$?
And what is $a_9$?
alex31415
2012-03-30 19:14:40
363
363
kmc927
2012-03-30 19:14:40
363
363
cerberus88
2012-03-30 19:14:40
363
363
TigerSneak1
2012-03-30 19:14:40
33
33
joshxiong
2012-03-30 19:14:40
27*(11/3)*(11/3)=363
27*(11/3)*(11/3)=363
silvernight
2012-03-30 19:14:40
363
363
numbertheorist17
2012-03-30 19:14:40
27*121/9=363
27*121/9=363
TigerSneak1
2012-03-30 19:14:40
363
363
cerberus88
2012-03-30 19:14:40
(r^4)^2*a=(11/3)^2*27=363
(r^4)^2*a=(11/3)^2*27=363
copeland
2012-03-30 19:14:45
We know that $a_1=27$, so \[a_9=ar^9=(ar)(r^8)=a_1(r^4)^2=27\left(\frac{11}{3}\right)^2=363.\]
We know that $a_1=27$, so \[a_9=ar^9=(ar)(r^8)=a_1(r^4)^2=27\left(\frac{11}{3}\right)^2=363.\]
copeland
2012-03-30 19:14:52
$\boxed{363}$ is the answer.
$\boxed{363}$ is the answer.
copeland
2012-03-30 19:15:12
3. At a certain university, the division of mathematical sciences consists of the departments of mathematics, statistics, and computer science. There are two male and two female professors in each department. A committee of six professors is to contain three men and three women and must also contain two professors from each of the three departments. Find the number of possible committees that can be formed subject to these requirements.
3. At a certain university, the division of mathematical sciences consists of the departments of mathematics, statistics, and computer science. There are two male and two female professors in each department. A committee of six professors is to contain three men and three women and must also contain two professors from each of the three departments. Find the number of possible committees that can be formed subject to these requirements.
copeland
2012-03-30 19:15:26
OK, counting problem. We're trying to build a committee, so this looks like a nice place for a constructive approach.
OK, counting problem. We're trying to build a committee, so this looks like a nice place for a constructive approach.
pl210741
2012-03-30 19:15:46
Casework!
Casework!
Hydroxide
2012-03-30 19:15:46
ughh casework
ughh casework
ABCDE
2012-03-30 19:15:46
Casework.
Casework.
MNL9082
2012-03-30 19:15:46
casework time
casework time
ytao
2012-03-30 19:15:46
Casework!
Casework!
lucylai
2012-03-30 19:15:46
or casework!!!
or casework!!!
deepankar
2012-03-30 19:15:46
casework
casework
copeland
2012-03-30 19:15:48
Let's think just about the genders of the committee members. The committee could, for example, look like MW MW MW or it could be MM MW WW or many other things.
Let's think just about the genders of the committee members. The committee could, for example, look like MW MW MW or it could be MM MW WW or many other things.
copeland
2012-03-30 19:15:54
The committee we want to construct has 3 men and 3 women. How do we count the ways to pick 3 of each from the 3 departments where 2 professors come from each department?
The committee we want to construct has 3 men and 3 women. How do we count the ways to pick 3 of each from the 3 departments where 2 professors come from each department?
mathswimmer
2012-03-30 19:17:05
from each department, you either take two of the same gender, or one of each
from each department, you either take two of the same gender, or one of each
joshxiong
2012-03-30 19:17:05
First case: MW from all 3 departments.
First case: MW from all 3 departments.
googol.plex
2012-03-30 19:17:05
There are 2 cases, one where all of the departments are male and the other are female and one where 1 has 2 male, 1 has 1 of each, and 1 has 2 females
There are 2 cases, one where all of the departments are male and the other are female and one where 1 has 2 male, 1 has 1 of each, and 1 has 2 females
lazorpenguin27143
2012-03-30 19:17:05
One man and one woman from each department is on the committee and One department has two men, another has two women, and the last has one of each.
One man and one woman from each department is on the committee and One department has two men, another has two women, and the last has one of each.
ABCDE
2012-03-30 19:17:05
MM FF MF and MF MF MF
MM FF MF and MF MF MF
ahaanomegas
2012-03-30 19:17:05
Case 1: One male and one female from each subject.
Case 1: One male and one female from each subject.
19oshawott98
2012-03-30 19:17:05
mm,ff,mf or mfmfmf
mm,ff,mf or mfmfmf
copeland
2012-03-30 19:17:09
We have cases. Either all of the women come from the different departments, or 2 women come from a single department.
We have cases. Either all of the women come from the different departments, or 2 women come from a single department.
copeland
2012-03-30 19:17:12
How many ways can we pick one woman and one man from each department?
How many ways can we pick one woman and one man from each department?
copeland
2012-03-30 19:17:27
(total.)
(total.)
centralbs
2012-03-30 19:17:52
4^3=64
4^3=64
lazorpenguin27143
2012-03-30 19:17:52
4^3 = 64
4^3 = 64
mjseaman1
2012-03-30 19:17:52
2^6=64 ways.
2^6=64 ways.
EuclidGenius
2012-03-30 19:17:52
4^3
4^3
nmandi7
2012-03-30 19:17:52
4^3=64
4^3=64
va2010
2012-03-30 19:17:52
2*2*2*2*2*2=64
2*2*2*2*2*2=64
joshxiong
2012-03-30 19:17:52
2^6=64.
2^6=64.
EuclidGenius
2012-03-30 19:17:52
$4^3=64$ total ways
$4^3=64$ total ways
sinnoel
2012-03-30 19:17:52
64
64
nackster12
2012-03-30 19:17:52
2^6=64
2^6=64
zinko1991
2012-03-30 19:17:52
2^6=64
2^6=64
copeland
2012-03-30 19:17:57
Each department has 2 choices for each of the male and female representatives it contributes. So each department has 4 possibilities. Since there are 3 departments, there are $4^3=64$ ways to pick one man and one woman from each department.
Each department has 2 choices for each of the male and female representatives it contributes. So each department has 4 possibilities. Since there are 3 departments, there are $4^3=64$ ways to pick one man and one woman from each department.
copeland
2012-03-30 19:18:04
How many total committees have 2 women from the same department?
How many total committees have 2 women from the same department?
lazorpenguin27143
2012-03-30 19:18:58
6*4 = 24
6*4 = 24
kmc927
2012-03-30 19:18:58
6*4=24
6*4=24
ABCDE
2012-03-30 19:18:58
6*2*2=24
6*2*2=24
va2010
2012-03-30 19:18:58
3*2*4=24
3*2*4=24
nmandi7
2012-03-30 19:18:58
24
24
admin25
2012-03-30 19:18:58
3 ways to pick department with all women, 2 with all men, and 2*2 ways to pick the last two. 3*2*2*2=24
3 ways to pick department with all women, 2 with all men, and 2*2 ways to pick the last two. 3*2*2*2=24
nackster12
2012-03-30 19:18:58
6*(1*4*1)=24
6*(1*4*1)=24
awesomemathlete
2012-03-30 19:18:58
24
24
joshxiong
2012-03-30 19:18:58
3*2*2*2=24
3*2*2*2=24
copeland
2012-03-30 19:19:03
The only way to distribute the committee members with 2 women from the same department is by having one department contribute 2 women, one department contribute 1 woman and one department contribute 0 women.
The only way to distribute the committee members with 2 women from the same department is by having one department contribute 2 women, one department contribute 1 woman and one department contribute 0 women.
copeland
2012-03-30 19:19:13
There are 3 choices for which department contributes the 2 women and there are 2 choices for which other department contributes the other woman. After these choices are made, the 2 women from the same department and the 2 men from the other department are determined. This leaves only 4 ways to choose the man and woman from the department that contributes one of each. There are $3\cdot2\cdot4=24$ total committees that can be formed in this way.
There are 3 choices for which department contributes the 2 women and there are 2 choices for which other department contributes the other woman. After these choices are made, the 2 women from the same department and the 2 men from the other department are determined. This leaves only 4 ways to choose the man and woman from the department that contributes one of each. There are $3\cdot2\cdot4=24$ total committees that can be formed in this way.
copeland
2012-03-30 19:19:17
And the total?
And the total?
sonchecky
2012-03-30 19:19:53
88
88
alex31415
2012-03-30 19:19:53
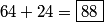
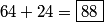
matholympiad25
2012-03-30 19:19:53
64+24=88
64+24=88
Flamewire
2012-03-30 19:19:53
88
88
Seedleaf
2012-03-30 19:19:53
64+24 = 88
64+24 = 88
Imsacred
2012-03-30 19:19:53
24 + 64 = 088
24 + 64 = 088
kmc927
2012-03-30 19:19:53
88
88
admin25
2012-03-30 19:19:53
64+24= $ \boxed{088} $
64+24= $ \boxed{088} $
CantonMathGuy
2012-03-30 19:19:53
88
88
PERFECTION
2012-03-30 19:19:53
64+24=88 total possible comittees
64+24=88 total possible comittees
jiyer99
2012-03-30 19:19:53
88
88
Mary_Posa
2012-03-30 19:19:53
88
88
ABCDE
2012-03-30 19:19:53
64+24=088
64+24=088
Hydroxide
2012-03-30 19:19:53
24+64=88
24+64=88
sarvottam
2012-03-30 19:19:53
88
88
copeland
2012-03-30 19:19:57
There are $64+24=\boxed{088}$ total ways to form such a committee.
There are $64+24=\boxed{088}$ total ways to form such a committee.
copeland
2012-03-30 19:20:05
3 down. . .
3 down. . .
ABCDE
2012-03-30 19:20:36
12 to go!
12 to go!
MNL9082
2012-03-30 19:20:36
12 to go
12 to go
EuclidGenius
2012-03-30 19:20:36
12 left
12 left
awesomemathlete
2012-03-30 19:20:36
12 to go
12 to go
theone142857
2012-03-30 19:20:36
12 to go
12 to go
copeland
2012-03-30 19:20:38
Yep. You don't actually get any points for that, though.
Yep. You don't actually get any points for that, though.
copeland
2012-03-30 19:20:39
4. Ana, Bob, and Cao bike at constant rates of 8.6 meters per second, 6.2 meters per second, and 5 meters per second, respectively. They all begin biking at the same time from the northeast corner of a rectangular field whose longer side runs due west. Ana starts biking along the edge of the field, initially heading west, Bob starts biking along the edge of the field, initially heading south, and Cao bikes in a straight line across the field to a point $D$ on the south edge of the field. Cao arrives at point $D$ at the same time that Ana and Bob arrive at $D$ for the first time. The ratio of the field's length to the field's width to the distance from the point $D$ to the southeast corner of the field can be represented as $p:q:r$, where $p$, $q$, and $r$ are positive integers with $p$ and $q$ relatively prime. Find $p + q + r$.
4. Ana, Bob, and Cao bike at constant rates of 8.6 meters per second, 6.2 meters per second, and 5 meters per second, respectively. They all begin biking at the same time from the northeast corner of a rectangular field whose longer side runs due west. Ana starts biking along the edge of the field, initially heading west, Bob starts biking along the edge of the field, initially heading south, and Cao bikes in a straight line across the field to a point $D$ on the south edge of the field. Cao arrives at point $D$ at the same time that Ana and Bob arrive at $D$ for the first time. The ratio of the field's length to the field's width to the distance from the point $D$ to the southeast corner of the field can be represented as $p:q:r$, where $p$, $q$, and $r$ are positive integers with $p$ and $q$ relatively prime. Find $p + q + r$.
copeland
2012-03-30 19:20:52
Yuck, yuck, yuck.
Yuck, yuck, yuck.
copeland
2012-03-30 19:20:56
That is a LOT of words.
That is a LOT of words.
copeland
2012-03-30 19:21:05
What should we do?
What should we do?
WAGE
2012-03-30 19:21:33
Diagram.
Diagram.
deepankar
2012-03-30 19:21:33
draw a picture
draw a picture
ahaanomegas
2012-03-30 19:21:33
Draw a diagram!
Draw a diagram!
joshxiong
2012-03-30 19:21:33
Draw a diagram.
Draw a diagram.
Imsacred
2012-03-30 19:21:33
diagram!
diagram!
shreyash
2012-03-30 19:21:33
make a diagram
make a diagram
Mattchu386
2012-03-30 19:21:33
Draw a diagram!
Draw a diagram!
TigerSneak1
2012-03-30 19:21:33
Draw a pretty picture
Draw a pretty picture
lucylai
2012-03-30 19:21:33
diagram
diagram
lily6481
2012-03-30 19:21:33
draw a picture
draw a picture
lucylai
2012-03-30 19:21:33
picture
picture
ptea
2012-03-30 19:21:33
draw a picture!
draw a picture!
mathnerd101
2012-03-30 19:21:33
draw a picture
draw a picture
copeland
2012-03-30 19:21:37
Draw a diagram!
Draw a diagram!
AbsoluteFriend
2012-03-30 19:21:44
Re-read.
Re-read.
EuclidGenius
2012-03-30 19:21:44
Read it. :)
Read it. :)
copeland
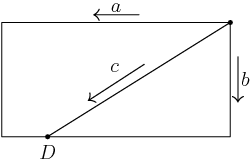
2012-03-30 19:21:47
Also, don't forget to read the problem carefully. Since we want the the longer side to run due west, we should draw our diagram to reflect that.
Also, don't forget to read the problem carefully. Since we want the the longer side to run due west, we should draw our diagram to reflect that.
copeland
2012-03-30 19:21:55

copeland
2012-03-30 19:22:05
The each start biking from the top right corner in the indicated directions. They meet at the point $D$.
The each start biking from the top right corner in the indicated directions. They meet at the point $D$.
copeland
2012-03-30 19:22:16
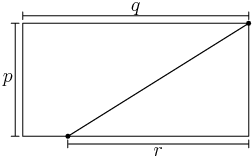
We should also label the distances we want. I have no idea what the words "length" and "width" mean, but we want their sum anyway, so it doesn't matter which one is which. I labeled my diagram by letting the length be the up-and-down direction:
We should also label the distances we want. I have no idea what the words "length" and "width" mean, but we want their sum anyway, so it doesn't matter which one is which. I labeled my diagram by letting the length be the up-and-down direction:
copeland
2012-03-30 19:22:35

copeland
2012-03-30 19:22:46
In terms of $p$, $q$, and $r$, how far did Bob bike?
In terms of $p$, $q$, and $r$, how far did Bob bike?
lucylai
2012-03-30 19:23:15
p+r
p+r
nackster12
2012-03-30 19:23:15
p+r
p+r
Flamewire
2012-03-30 19:23:15
p + r
p + r
centralbs
2012-03-30 19:23:15
p+r
p+r
zinko1991
2012-03-30 19:23:15
p+r
p+r
proglote
2012-03-30 19:23:15
p + r
p + r
King6997
2012-03-30 19:23:15
r+p
r+p
ytao
2012-03-30 19:23:15
p+r
p+r
claudiafeng
2012-03-30 19:23:15
p+r
p+r
lily6481
2012-03-30 19:23:15
p+r
p+r
copeland
2012-03-30 19:23:16
Bob biked down the right side and over to $D$. His path has length $p+r$.
Bob biked down the right side and over to $D$. His path has length $p+r$.
copeland
2012-03-30 19:23:21
How far did Ana bike in terms of $p$, $q$, and $r$?
How far did Ana bike in terms of $p$, $q$, and $r$?
sonchecky
2012-03-30 19:24:13
$2q+p-r$
$2q+p-r$
lucylai
2012-03-30 19:24:13
p+2q-r
p+2q-r
19oshawott98
2012-03-30 19:24:13
q+p+q-r
q+p+q-r
AbsoluteFriend
2012-03-30 19:24:13
r+p
r+p
googol.plex
2012-03-30 19:24:13
p+2q-r
p+2q-r
admin25
2012-03-30 19:24:13
p+q+(q-r)=2q+p-r
p+q+(q-r)=2q+p-r
Flamewire
2012-03-30 19:24:13
2q + p -r
2q + p -r
ABCDE
2012-03-30 19:24:13
p+2q-r
p+2q-r
copeland
2012-03-30 19:24:15
Ana biked across the top ($q$), then down the side ($p$), and then across the segment of length $q-r$ from the southwest corner to $D$. So Ana biked a distance of \[q+p+(q-r)=p+2q-r.\]
Ana biked across the top ($q$), then down the side ($p$), and then across the segment of length $q-r$ from the southwest corner to $D$. So Ana biked a distance of \[q+p+(q-r)=p+2q-r.\]
copeland
2012-03-30 19:24:18
As a check we note that Ana and Bob combined biked $(p+r)+(p+2q-r)=2p+2q$, which is the entire perimeter of the field.
As a check we note that Ana and Bob combined biked $(p+r)+(p+2q-r)=2p+2q$, which is the entire perimeter of the field.
copeland
2012-03-30 19:24:23
How far did Cao bike?
How far did Cao bike?
claudiafeng
2012-03-30 19:24:53
$\sqrt{p^2+r^2}$
$\sqrt{p^2+r^2}$
ahaanomegas
2012-03-30 19:24:53
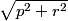
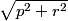
alex31415
2012-03-30 19:24:53
sqrt(p^2+r^2)
sqrt(p^2+r^2)
himym83
2012-03-30 19:24:53
sqrt(p^2+r^2)
sqrt(p^2+r^2)
deepankar
2012-03-30 19:24:53
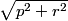
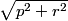
Seedleaf
2012-03-30 19:24:53
sqrt(p^2+r^2)
sqrt(p^2+r^2)
joshxiong
2012-03-30 19:24:53
$\sqrt{p^2+r^2}$
$\sqrt{p^2+r^2}$
PERFECTION
2012-03-30 19:24:53
sqrt(r^2+p^2)
sqrt(r^2+p^2)
sinnoel
2012-03-30 19:24:53
sqrt(p^2+r^2)
sqrt(p^2+r^2)
sonchecky
2012-03-30 19:24:57
$\sqrt{q^2+r^2} by the Pythagorean Theorem
$\sqrt{q^2+r^2} by the Pythagorean Theorem
admin25
2012-03-30 19:24:57
$ \sqrt{p^2+r^2} $, by pythagorean theorem (blech, radicals)
$ \sqrt{p^2+r^2} $, by pythagorean theorem (blech, radicals)
copeland
2012-03-30 19:25:01
By the Pythagorean Theorem, Cao biked a total distance of $\sqrt{p^2+r^2}$.
By the Pythagorean Theorem, Cao biked a total distance of $\sqrt{p^2+r^2}$.
copeland
2012-03-30 19:25:05
So the ratio of the distances that they traveled is \[a:b:c=p+2q-r:p+r:\sqrt{p^2+q^2}.\]
So the ratio of the distances that they traveled is \[a:b:c=p+2q-r:p+r:\sqrt{p^2+q^2}.\]
copeland
2012-03-30 19:25:08
Do we know anything else about this ratio?
Do we know anything else about this ratio?
copeland
2012-03-30 19:25:59
Typo up there:
Typo up there:
copeland
2012-03-30 19:26:03
So the ratio of the distances that they traveled is \[a:b:c=p+2q-r:p+r:\sqrt{p^2+r^2}.\]
So the ratio of the distances that they traveled is \[a:b:c=p+2q-r:p+r:\sqrt{p^2+r^2}.\]
ABCDE
2012-03-30 19:26:08
8.6:6.2:5
8.6:6.2:5
TigerSneak1
2012-03-30 19:26:08
It's also 8.6 to 6.2 to 5
It's also 8.6 to 6.2 to 5
googol.plex
2012-03-30 19:26:08
it should be 8.6:6.2:5
it should be 8.6:6.2:5
mathswimmer
2012-03-30 19:26:08
same as velocity
same as velocity
centralbs
2012-03-30 19:26:08
since d=rt and the time is equal, d/r is constant
since d=rt and the time is equal, d/r is constant
MNL9082
2012-03-30 19:26:08
it equals the ratio of their speeds
it equals the ratio of their speeds
brokenfixer
2012-03-30 19:26:08
8.6:6.2:5
8.6:6.2:5
CantonMathGuy
2012-03-30 19:26:08
use speeds
use speeds
copeland
2012-03-30 19:26:13
It's given in the problem! We know the ratios of their speeds, and if they travel for the same amount of time, that will also be the ratio of the distances that they travel. \[a:b:c=8.6:6.2:5.\]
It's given in the problem! We know the ratios of their speeds, and if they travel for the same amount of time, that will also be the ratio of the distances that they travel. \[a:b:c=8.6:6.2:5.\]
copeland
2012-03-30 19:26:17
I'm compelled to clean that up by multiplying by 5.
I'm compelled to clean that up by multiplying by 5.
copeland
2012-03-30 19:26:22
\[a:b:c=43:31:25.\]
\[a:b:c=43:31:25.\]
copeland
2012-03-30 19:26:33
Now what?
Now what?
sparkle123
2012-03-30 19:27:12
Set r=1.
Set r=1.
AbsoluteFriend
2012-03-30 19:27:17
Equate them.
Equate them.
Flamewire
2012-03-30 19:27:17
Set up a system of equations
Set up a system of equations
googol.plex
2012-03-30 19:27:17
system of equations
system of equations
shreyash
2012-03-30 19:27:17
make equations
make equations
ptea
2012-03-30 19:27:17
solve that mess
solve that mess
kmc927
2012-03-30 19:27:17
solve for p q & r
solve for p q & r
nackster12
2012-03-30 19:27:17
set the ratios equal to each other and solve (ew)
set the ratios equal to each other and solve (ew)
flyrain
2012-03-30 19:27:17
use these in p, q, and r, so we can system of equations
use these in p, q, and r, so we can system of equations
copeland
2012-03-30 19:27:22
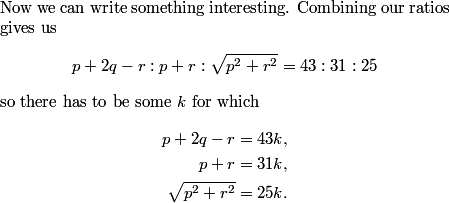
copeland
2012-03-30 19:27:24
Hmm. This makes things harder for us than they need to be. What should we do instead?
Hmm. This makes things harder for us than they need to be. What should we do instead?
alex31415
2012-03-30 19:27:51
Can we assume the width is 1 and multiply by an appropriate scale factor at the end?
Can we assume the width is 1 and multiply by an appropriate scale factor at the end?
ahaanomegas
2012-03-30 19:27:51
On the actual test, I called the time t and, not too long after, I assumed WLOG that t = 10.
On the actual test, I called the time t and, not too long after, I assumed WLOG that t = 10.
shreyash
2012-03-30 19:27:51
set k = 1
set k = 1
Flamewire
2012-03-30 19:27:51
WLOG assume k = 1
WLOG assume k = 1
nackster12
2012-03-30 19:27:51
let k=1
let k=1
robinpark
2012-03-30 19:27:51
let k = 1
let k = 1
nmandi7
2012-03-30 19:27:51
k=1
k=1
copeland
2012-03-30 19:27:55
We don't really need to worry about units at this point. It's actually fair just to throw the $k$ away. After all we want a ratio for our final answer and not actual values.
We don't really need to worry about units at this point. It's actually fair just to throw the $k$ away. After all we want a ratio for our final answer and not actual values.
copeland
2012-03-30 19:28:00
\begin{align*}
p+2q-r&=43,\\
p+r&=31,\\
\sqrt{p^2+r^2}&=25.
\end{align*}
\begin{align*}
p+2q-r&=43,\\
p+r&=31,\\
\sqrt{p^2+r^2}&=25.
\end{align*}
copeland
2012-03-30 19:28:06
Three equations in three unknowns so we should be able to solve. Where should we start?
Three equations in three unknowns so we should be able to solve. Where should we start?
ytao
2012-03-30 19:28:47
Square the latter.
Square the latter.
Flamewire
2012-03-30 19:28:47
Square the third equation
Square the third equation
CantonMathGuy
2012-03-30 19:28:47
square the third equation
square the third equation
lazorpenguin27143
2012-03-30 19:28:47
square the last equation
square the last equation
zinko1991
2012-03-30 19:28:47
3rd equation
3rd equation
Hydroxide
2012-03-30 19:28:47
square last equation
square last equation
Flamewire
2012-03-30 19:28:47
Square the third equation, set p^2 + r^2 = (p+r)^2 - 2pr = 25
Square the third equation, set p^2 + r^2 = (p+r)^2 - 2pr = 25
sinnoel
2012-03-30 19:28:47
2nd and 3rd equation
2nd and 3rd equation
MNL9082
2012-03-30 19:28:47
use the bottom two equations
use the bottom two equations
copeland
2012-03-30 19:28:52
Since the last two equations only deal with $p$ and $r$, we should start with those. What's the first step in dealing with
\begin{align*}
p+r&=31,\\
\sqrt{p^2+r^2}&=25?
\end{align*}
Since the last two equations only deal with $p$ and $r$, we should start with those. What's the first step in dealing with
\begin{align*}
p+r&=31,\\
\sqrt{p^2+r^2}&=25?
\end{align*}
copeland
2012-03-30 19:28:56
Let's square the bottom equation:\[p^2+r^2=625.\]
Let's square the bottom equation:\[p^2+r^2=625.\]
copeland
2012-03-30 19:29:01
What else?
What else?
ABCDE
2012-03-30 19:29:43
square the first one and subtrack
square the first one and subtrack
brokenfixer
2012-03-30 19:29:43
square the top equation
square the top equation
lazorpenguin27143
2012-03-30 19:29:43
square p+r = 31
square p+r = 31
centralbs
2012-03-30 19:29:43
square the top equation and subtract
square the top equation and subtract
DF2222
2012-03-30 19:29:43
square the top equation
square the top equation
robinpark
2012-03-30 19:29:43
Square $p+r$ then subtract $p^2 + r^2$
Square $p+r$ then subtract $p^2 + r^2$
Seedleaf
2012-03-30 19:29:43
square the top one to create square values
square the top one to create square values
lily6481
2012-03-30 19:29:43
square p+r
square p+r
pl210741
2012-03-30 19:29:45
square the first equation
square the first equation
copeland
2012-03-30 19:29:48
This is quadratic, so it might help to make the other equation quadratic, too:
This is quadratic, so it might help to make the other equation quadratic, too:
copeland
2012-03-30 19:29:53
\begin{align*}
p^2+2pr+r^2&=961,\\
p^2+r^2&=625.
\end{align*}
\begin{align*}
p^2+2pr+r^2&=961,\\
p^2+r^2&=625.
\end{align*}
copeland
2012-03-30 19:29:57
So we could subtract those to get $2pr$, and that might be helpful, but what else could we get that would be more helpful?
So we could subtract those to get $2pr$, and that might be helpful, but what else could we get that would be more helpful?
brokenfixer
2012-03-30 19:30:42
(p-r)^2
(p-r)^2
AbsoluteFriend
2012-03-30 19:30:42
A difference of two squares.
A difference of two squares.
admin25
2012-03-30 19:30:42
$ p-r $, so we can substitute that into the first equation!
$ p-r $, so we can substitute that into the first equation!
copeland
2012-03-30 19:30:44
Good!
Good!
copeland
2012-03-30 19:30:46
Wait, how?
Wait, how?
brokenfixer
2012-03-30 19:31:54
625 - (961-625)
625 - (961-625)
proglote
2012-03-30 19:31:54
get 2pr first
get 2pr first
sonchecky
2012-03-30 19:31:54
Subtract twice the second equation minus the first.
Subtract twice the second equation minus the first.
admin25
2012-03-30 19:31:54
subtract $ 4pr $ from $ (p+r)^2 $ to get $ (p-r)^2 $
subtract $ 4pr $ from $ (p+r)^2 $ to get $ (p-r)^2 $
nackster12
2012-03-30 19:31:54
find 2pr then subtract 2pr from the bottom equation
find 2pr then subtract 2pr from the bottom equation
Imsacred
2012-03-30 19:31:54
find 2pr, then subtract 4pr from the first equation?
find 2pr, then subtract 4pr from the first equation?
alex31415
2012-03-30 19:31:54
(p-r)^2=289
(p-r)^2=289
copeland
2012-03-30 19:31:58
We notice that \[2(p^2+r^2)-(p^2+2pr+r^2)=p^2-2pr+r^2=(p-r)^2.\] That should be useful.
We notice that \[2(p^2+r^2)-(p^2+2pr+r^2)=p^2-2pr+r^2=(p-r)^2.\] That should be useful.
copeland
2012-03-30 19:32:05
Therefore\[(p-r)^2=2(p^2+r^2)-(p^2+2pr+r^2)=2\cdot625-961=289=17^2.\]
Therefore\[(p-r)^2=2(p^2+r^2)-(p^2+2pr+r^2)=2\cdot625-961=289=17^2.\]
copeland
2012-03-30 19:32:12
So what is $p-r$?
So what is $p-r$?
wmcho1007
2012-03-30 19:33:08
p-r=17
p-r=17
flyrain
2012-03-30 19:33:08
17
17
trident
2012-03-30 19:33:08
17
17
pl210741
2012-03-30 19:33:08
17
17
Hydroxide
2012-03-30 19:33:08
17
17
kmc927
2012-03-30 19:33:08
17
17
sonchecky
2012-03-30 19:33:08
17
17
lazorpenguin27143
2012-03-30 19:33:08
17
17
sinnoel
2012-03-30 19:33:08
17
17
matholympiad25
2012-03-30 19:33:08
17
17
ashgabat
2012-03-30 19:33:08
17.
17.
googol.plex
2012-03-30 19:33:08
17, but we know p+r is 31 so we have r!
17, but we know p+r is 31 so we have r!
alex31415
2012-03-30 19:33:08
p-r=17, p+r=31, solve!
p-r=17, p+r=31, solve!
FunnyBounny
2012-03-30 19:33:08
17
17
ytao
2012-03-30 19:33:08
$\sqrt{17^2}=17$
$\sqrt{17^2}=17$
TigerSneak1
2012-03-30 19:33:08
17
17
EuclidGenius
2012-03-30 19:33:08
17
17
sarvottam
2012-03-30 19:33:08
17
17
bunniesrcute
2012-03-30 19:33:08
17
17
Leafpelt
2012-03-30 19:33:08
17
17
shreyash
2012-03-30 19:33:08
17
17
EuclidGenius
2012-03-30 19:33:08
17
17
zinko1991
2012-03-30 19:33:08
17
17
ahaanomegas
2012-03-30 19:33:08
17
17
iamthygod!!!!!!
2012-03-30 19:33:08
the square root of 17^2, which is 17
the square root of 17^2, which is 17
copeland
2012-03-30 19:33:10
No!
No!
copeland
2012-03-30 19:33:15
Hrm.
Hrm.
copeland
2012-03-30 19:33:36
This is why I missed this problem, too. :)
This is why I missed this problem, too. :)
nackster12
2012-03-30 19:33:53
17 or -17
17 or -17
DF2222
2012-03-30 19:33:53
plus or minus 17
plus or minus 17
MNL9082
2012-03-30 19:33:53
plus or minus 17?
plus or minus 17?
nackster12
2012-03-30 19:33:53
could be negative
could be negative
matholympiad25
2012-03-30 19:33:53
COULD IT BE -17?
COULD IT BE -17?
kmc927
2012-03-30 19:33:53
or -17?
or -17?
dantx5
2012-03-30 19:33:53
+/- 17?
+/- 17?
wmcho1007
2012-03-30 19:33:53
or maybe -17?
or maybe -17?
waveahu
2012-03-30 19:33:53
plus or minus 17?
plus or minus 17?
shreyash
2012-03-30 19:33:53
it can also be -17
it can also be -17
matholympiad25
2012-03-30 19:33:53
Couldn't it also be -17?
Couldn't it also be -17?
mathnerd101
2012-03-30 19:33:53
it could be -17 too
it could be -17 too
copeland
2012-03-30 19:34:00
Careful! This is the trickiest part of this problem. We know that $p-r=\pm17$, but we don't yet know the sign.
Careful! This is the trickiest part of this problem. We know that $p-r=\pm17$, but we don't yet know the sign.
copeland
2012-03-30 19:34:04
What are $p$ and $r$?
What are $p$ and $r$?
alex31415
2012-03-30 19:34:56
24 and 7, respectively
24 and 7, respectively
matholympiad25
2012-03-30 19:34:56
if p-r = -17, p+r = 31, p = 7, r = 24
if p-r = -17, p+r = 31, p = 7, r = 24
TigerSneak1
2012-03-30 19:34:56
one is 24 and the other 7, but we don't know which.
one is 24 and the other 7, but we don't know which.
wmcho1007
2012-03-30 19:34:56
7 and 24?
7 and 24?
MNL9082
2012-03-30 19:34:56
24 and 7
24 and 7
googol.plex
2012-03-30 19:34:56
well r is either 24 or 7
well r is either 24 or 7
nmandi7
2012-03-30 19:34:57
24 and 7
24 and 7
copeland
2012-03-30 19:35:01
If the sum of two numbers is 31 and the difference is 17, then the two numbers must be 24 and 7. We just don't know the order yet.
If the sum of two numbers is 31 and the difference is 17, then the two numbers must be 24 and 7. We just don't know the order yet.
copeland
2012-03-30 19:35:08
If $p=7$ and $r=24$ then what is $q$?
If $p=7$ and $r=24$ then what is $q$?
lazorpenguin27143
2012-03-30 19:35:38
30
30
lucylai
2012-03-30 19:35:38
30
30
Hydroxide
2012-03-30 19:35:38
30
30
ytao
2012-03-30 19:35:38
30
30
Seedleaf
2012-03-30 19:35:38
q = 30
q = 30
Imsacred
2012-03-30 19:35:38
30
30
zinko1991
2012-03-30 19:35:38
30
30
kmc927
2012-03-30 19:35:38
30
30
admin25
2012-03-30 19:35:38
$ 60/3=30 $
$ 60/3=30 $
copeland
2012-03-30 19:35:42
If $p=7$ and $r=24$ then \[q=\frac{43+r-p}2=\frac{43+17}2=30.\]
If $p=7$ and $r=24$ then \[q=\frac{43+r-p}2=\frac{43+17}2=30.\]
copeland
2012-03-30 19:35:51
If $p=24$ and $r=7$ then what is $q$?
If $p=24$ and $r=7$ then what is $q$?
Fire-Sword
2012-03-30 19:36:41
13
13
ptes77
2012-03-30 19:36:41
13
13
Seedleaf
2012-03-30 19:36:41
q = 13
q = 13
lucylai
2012-03-30 19:36:41
13
13
joshxiong
2012-03-30 19:36:41
13
13
mathswimmer
2012-03-30 19:36:41
13
13
iamthygod!!!!!!
2012-03-30 19:36:41
13
13
copeland
2012-03-30 19:36:47
If $p=24$ and $r=7$ then \[q=\frac{43+r-p}2=\frac{43-17}2=13.\]
If $p=24$ and $r=7$ then \[q=\frac{43+r-p}2=\frac{43-17}2=13.\]
copeland
2012-03-30 19:36:50
Hmm. Are there two solutions?
Hmm. Are there two solutions?
nackster12
2012-03-30 19:37:29
13 but q cant be less than p according to the problem
13 but q cant be less than p according to the problem
Flamewire
2012-03-30 19:37:29
Which can't work because q > p
Which can't work because q > p
GeorgiaTechMan
2012-03-30 19:37:29
but p>q
but p>q
Mary_Posa
2012-03-30 19:37:29
no, 13 is less than 24
no, 13 is less than 24
himym83
2012-03-30 19:37:29
no, we are told that q>p
no, we are told that q>p
sonchecky
2012-03-30 19:37:29
No - q must be greater than p because the field's longer side runs west.
No - q must be greater than p because the field's longer side runs west.
shreyash
2012-03-30 19:37:29
q has to greater than p therefore q is 30, p = 7, r = 24
q has to greater than p therefore q is 30, p = 7, r = 24
sarvottam
2012-03-30 19:37:29
no
no
m1sterzer0
2012-03-30 19:37:29
long side of the rectangles runs east to west
long side of the rectangles runs east to west
copeland
2012-03-30 19:37:33
No! We also assumed that $p<q$. Since 24 is greater than 13, we cannot have $p=24$ and $q=13$. Therefore $p:q:r=7:30:24$.
No! We also assumed that $p<q$. Since 24 is greater than 13, we cannot have $p=24$ and $q=13$. Therefore $p:q:r=7:30:24$.
copeland
2012-03-30 19:37:36
What is the answer?
What is the answer?
EuclidGenius
2012-03-30 19:38:07
061
061
flyrain
2012-03-30 19:38:07
61
61
proglote
2012-03-30 19:38:07
061
061
claudiafeng
2012-03-30 19:38:07
61
61
ABCDE
2012-03-30 19:38:07
7+30+24=061
7+30+24=061
trident
2012-03-30 19:38:07
7+30+24 = 061
7+30+24 = 061
ytao
2012-03-30 19:38:07
30+24+7=061
30+24+7=061
CantonMathGuy
2012-03-30 19:38:07
61
61
hatchguy
2012-03-30 19:38:07
61
61
AbsoluteFriend
2012-03-30 19:38:07
61
61
ptes77
2012-03-30 19:38:07
61
61
copeland
2012-03-30 19:38:11
Since these integers are relatively prime, the answer is the sum: $p+q+r=7+30+24=\boxed{061}$.
Since these integers are relatively prime, the answer is the sum: $p+q+r=7+30+24=\boxed{061}$.
copeland
2012-03-30 19:38:26
5. In the accompanying figure, the outer square $S$ has side length 40. A second square $S'$ of side length 15 is constructed inside $S$ with the same center as $S$ and with sides parallel to those of $S$. From each midpoint of a side of $S$, segments are drawn to the two closest vertices of $S'$. The result is a four-pointed starlike figure inscribed in $S$. The star figure is cut out and then folded to form a pyramid with base $S'$. Find the volume of this pyramid.
5. In the accompanying figure, the outer square $S$ has side length 40. A second square $S'$ of side length 15 is constructed inside $S$ with the same center as $S$ and with sides parallel to those of $S$. From each midpoint of a side of $S$, segments are drawn to the two closest vertices of $S'$. The result is a four-pointed starlike figure inscribed in $S$. The star figure is cut out and then folded to form a pyramid with base $S'$. Find the volume of this pyramid.
copeland
2012-03-30 19:38:34
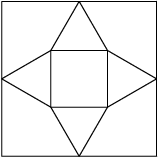

copeland
2012-03-30 19:38:41
Hope you guys brought your scissors.
Hope you guys brought your scissors.
copeland
2012-03-30 19:39:03
I like building these things out of cardboard and filling them with pudding.
I like building these things out of cardboard and filling them with pudding.
mathnerd101
2012-03-30 19:39:23
do we have to cut?
do we have to cut?
copeland
2012-03-30 19:39:24
Yes. Safety scissors for you, though!
Yes. Safety scissors for you, though!
copeland
2012-03-30 19:39:28
What's the easiest formula for the volume of a pyramid?
What's the easiest formula for the volume of a pyramid?
Flamewire
2012-03-30 19:39:55
Bh/3
Bh/3
alex31415
2012-03-30 19:39:55
1/3*b*h
1/3*b*h
googol.plex
2012-03-30 19:39:55
b*h/3
b*h/3
matholympiad25
2012-03-30 19:39:55
1/3 * base area * height
1/3 * base area * height
Voytek
2012-03-30 19:39:55
1/3 * base * height
1/3 * base * height
lily6481
2012-03-30 19:39:55
1/3bh
1/3bh
Past
2012-03-30 19:39:55
bh/3
bh/3
coldsummer
2012-03-30 19:39:55
1/3bh
1/3bh
TeamJacob
2012-03-30 19:39:55
bh/3
bh/3
copeland
2012-03-30 19:40:00
The volume is $\frac{Bh}3$, where $B$ is the area of the base, and $h$ is the height.
The volume is $\frac{Bh}3$, where $B$ is the area of the base, and $h$ is the height.
copeland
2012-03-30 19:40:06
Do we know either of these values?
Do we know either of these values?
copeland
2012-03-30 19:40:24
(Wait, I'm being told that pudding is not allowed on the AIME.)
(Wait, I'm being told that pudding is not allowed on the AIME.)
wmcho1007
2012-03-30 19:40:41
we have the base, which is 15*15=225
we have the base, which is 15*15=225
brokenfixer
2012-03-30 19:40:41
225
225
admin25
2012-03-30 19:40:41
Area of base=$ 15^2=225 $
Area of base=$ 15^2=225 $
centralbs
2012-03-30 19:40:41
B=225
B=225
deepankar
2012-03-30 19:40:41
we know side of square is 15, so B = 15^2 = 225
we know side of square is 15, so B = 15^2 = 225
MNL9082
2012-03-30 19:40:41
the base, 225
the base, 225
TigerSneak1
2012-03-30 19:40:41
we know the base, its 225
we know the base, its 225
ahaanomegas
2012-03-30 19:40:46
We know B, since the base is a square with side length 15.
We know B, since the base is a square with side length 15.
copeland
2012-03-30 19:40:49
The base is a square of side length 15, so $B=15^2.$
The base is a square of side length 15, so $B=15^2.$
copeland
2012-03-30 19:40:53
All we need is the height!
All we need is the height!
copeland
2012-03-30 19:40:57
Time to visualize:
Time to visualize:
copeland
2012-03-30 19:41:02
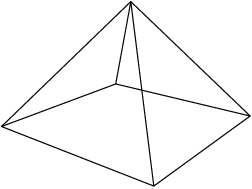

copeland
2012-03-30 19:41:05
We know the length of the base. What else can we compute easily?
We know the length of the base. What else can we compute easily?
GeorgiaTechMan
2012-03-30 19:41:42
lateral height
lateral height
trident
2012-03-30 19:41:42
find the lateral height of one of the triangles
find the lateral height of one of the triangles
centralbs
2012-03-30 19:41:42
The slant height
The slant height
heliootrope
2012-03-30 19:41:42
slant height
slant height
Potla
2012-03-30 19:41:42
Height of the side face
Height of the side face
Imsacred
2012-03-30 19:41:42
slant height
slant height
kmc927
2012-03-30 19:41:42
height of triangle
height of triangle
nmandi7
2012-03-30 19:41:42
the slant height
the slant height
lazorpenguin27143
2012-03-30 19:41:42
the altitude of the triangle faces
the altitude of the triangle faces
Voytek
2012-03-30 19:41:42
The distance from one edge to the top
The distance from one edge to the top
copeland
2012-03-30 19:41:46
We can compute the distance from the vertex to the midpoint of a side of the base:
We can compute the distance from the vertex to the midpoint of a side of the base:
copeland
2012-03-30 19:41:51


copeland
2012-03-30 19:41:53


copeland
2012-03-30 19:41:54
What is that distance?
What is that distance?
joshxiong
2012-03-30 19:42:33
Lateral Height=25/2
Lateral Height=25/2
Hydroxide
2012-03-30 19:42:33
25/2
25/2
lucylai
2012-03-30 19:42:33
25/2
25/2
jasonmathcounts
2012-03-30 19:42:33
12.5
12.5
wmcho1007
2012-03-30 19:42:33
(40-15)/2=25/2
(40-15)/2=25/2
ashgabat
2012-03-30 19:42:33
12.5
12.5
Seedleaf
2012-03-30 19:42:33
(40 - 15)/2 = 25/2
(40 - 15)/2 = 25/2
n2010Math
2012-03-30 19:42:33
25/2
25/2
DF2222
2012-03-30 19:42:33
12.5
12.5
copeland
2012-03-30 19:42:38
If that distance is $x$, then $x+15+x=40$, so $x=\frac{25}2$.
If that distance is $x$, then $x+15+x=40$, so $x=\frac{25}2$.
copeland
2012-03-30 19:42:41
What other distance can we compute easily?
What other distance can we compute easily?
himym83
2012-03-30 19:43:35
distance from edge to center of square
distance from edge to center of square
lazorpenguin27143
2012-03-30 19:43:35
the distance from the center of the circle to the side
the distance from the center of the circle to the side
danielguo94
2012-03-30 19:43:35
center to edge of square
center to edge of square
Past
2012-03-30 19:43:35
distance from a side to the center
distance from a side to the center
deepankar
2012-03-30 19:43:35
apothem of base
apothem of base
joshxiong
2012-03-30 19:43:35
distance from the center of the square to a midpoint
distance from the center of the square to a midpoint
mathnerd101
2012-03-30 19:43:35
half the side length of the base
half the side length of the base
copeland
2012-03-30 19:43:38
We can compute the distance from the center of the base to the midpoint of any base edge:
We can compute the distance from the center of the base to the midpoint of any base edge:
copeland
2012-03-30 19:43:42
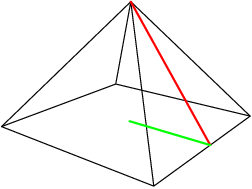

copeland
2012-03-30 19:43:46
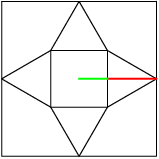

copeland
2012-03-30 19:43:47
How long is that segment?
How long is that segment?
EuclidGenius
2012-03-30 19:44:15
It is 15/2
It is 15/2
iamthygod!!!!!!
2012-03-30 19:44:15
7.5
7.5
shreyash
2012-03-30 19:44:15
7.5
7.5
ptes77
2012-03-30 19:44:15
15/2
15/2
Fire-Sword
2012-03-30 19:44:15
15/2
15/2
thunderPA
2012-03-30 19:44:15
7.5
7.5
ABCDE
2012-03-30 19:44:15
15/2
15/2
sarvottam
2012-03-30 19:44:15
15/2
15/2
sonchecky
2012-03-30 19:44:15
$15/2 = 7.5$
$15/2 = 7.5$
claudiafeng
2012-03-30 19:44:15
7.5
7.5
m1sterzer0
2012-03-30 19:44:15
15/2
15/2
admin25
2012-03-30 19:44:15
$ \frac{15}{2} $, half the side length of the square
$ \frac{15}{2} $, half the side length of the square
wlpj11
2012-03-30 19:44:15
15/2=7.5
15/2=7.5
copeland
2012-03-30 19:44:19
This is half the square, so has length $\frac{15}2$.
This is half the square, so has length $\frac{15}2$.
copeland
2012-03-30 19:44:23
What is the height of the pyramid?
What is the height of the pyramid?
copeland
2012-03-30 19:44:27
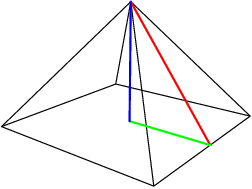

mathswimmer
2012-03-30 19:45:08
15/2 3-4-5 triangle!
15/2 3-4-5 triangle!
Larklight
2012-03-30 19:45:08
25/2^2-15/2^2=20/2=10
25/2^2-15/2^2=20/2=10
deepankar
2012-03-30 19:45:08
20/2 = 10 (it's a 3-4-5 right triangle)
20/2 = 10 (it's a 3-4-5 right triangle)
m1sterzer0
2012-03-30 19:45:08
20/2 (scaled 3-4-5 triangle)
20/2 (scaled 3-4-5 triangle)
mathswimmer
2012-03-30 19:45:08
it's a 3-4-5 triangle, so 20/5=10
it's a 3-4-5 triangle, so 20/5=10
flyrain
2012-03-30 19:45:08
20/2=10
20/2=10
newchie123
2012-03-30 19:45:08
10
10
Flamewire
2012-03-30 19:45:08
sqrt(625/4 - 225/4) = sqrt(400/4) = 10
sqrt(625/4 - 225/4) = sqrt(400/4) = 10
ytao
2012-03-30 19:45:08
By the Pythagorean Theorem, 20/2=10
By the Pythagorean Theorem, 20/2=10
Mattchu386
2012-03-30 19:45:08
it's a 3-4-5 right triangle, so 20/2=10.
it's a 3-4-5 right triangle, so 20/2=10.
coldsummer
2012-03-30 19:45:08
we can now use 7.5=a and 12.5=c and use the pythagorean theorem, which shows b=10
we can now use 7.5=a and 12.5=c and use the pythagorean theorem, which shows b=10
hrq
2012-03-30 19:45:08
10
10
theone142857
2012-03-30 19:45:08
10
10
copeland
2012-03-30 19:45:11
We have a right triangle here. it has hypotenuse $\frac{25}2$ and the green base is $\frac{15}2$. We notice that these are the dimensions of a $3-4-5$ triangle, with edges $\frac{15}2-\frac{20}2-\frac{25}2$. Therefore the height is $\frac{20}2=10$.
We have a right triangle here. it has hypotenuse $\frac{25}2$ and the green base is $\frac{15}2$. We notice that these are the dimensions of a $3-4-5$ triangle, with edges $\frac{15}2-\frac{20}2-\frac{25}2$. Therefore the height is $\frac{20}2=10$.
copeland
2012-03-30 19:45:19
What is the volume?
What is the volume?
ahaanomegas
2012-03-30 19:45:44


brokenfixer
2012-03-30 19:45:44
(1/3) * 225 * 10 = 750 !
(1/3) * 225 * 10 = 750 !
alex31415
2012-03-30 19:45:44
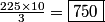
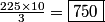
TeamJacob
2012-03-30 19:45:44
750
750
claudiafeng
2012-03-30 19:45:44
750
750
CantonMathGuy
2012-03-30 19:45:44
750
750
Imsacred
2012-03-30 19:45:44
1/3 * 10 * 15 * 15 = 750
1/3 * 10 * 15 * 15 = 750
Tigeraops
2012-03-30 19:45:44
750
750
nackster12
2012-03-30 19:45:44
225*10/3=750
225*10/3=750
matholympiad25
2012-03-30 19:45:44
1/3 * 10 * 15^2 = 750
1/3 * 10 * 15^2 = 750
TeamJacob
2012-03-30 19:45:44
225(10)/3 = 750
225(10)/3 = 750
copeland
2012-03-30 19:45:49
The volume is $\frac{15^2\cdot10}3=\boxed{750}.$
The volume is $\frac{15^2\cdot10}3=\boxed{750}.$
Past
2012-03-30 19:46:13
can I have your pudding recipe?
can I have your pudding recipe?
copeland
2012-03-30 19:46:14
No. My mom would KILL me. Family secrets. You understand, I'm sure.
No. My mom would KILL me. Family secrets. You understand, I'm sure.
copeland
2012-03-30 19:46:22
6. Let $z = a + bi$ be the complex number with $|z| = 5$ and $b > 0$ such that the distance between $(1 + 2i) z^3$ and $z^5$ is maximized, and let $z^4 = c + di$. Find $c + d$.
6. Let $z = a + bi$ be the complex number with $|z| = 5$ and $b > 0$ such that the distance between $(1 + 2i) z^3$ and $z^5$ is maximized, and let $z^4 = c + di$. Find $c + d$.
copeland
2012-03-30 19:46:36
Let's start with the distance statement. What is the distance from point $a$ to point $b$ in the complex plane?
Let's start with the distance statement. What is the distance from point $a$ to point $b$ in the complex plane?
proglote
2012-03-30 19:47:21
|a-b|
|a-b|
mathswimmer
2012-03-30 19:47:21
|a-b|
|a-b|
admin25
2012-03-30 19:47:21
|a-b|
|a-b|
sonchecky
2012-03-30 19:47:21
|a-b|
|a-b|
nackster12
2012-03-30 19:47:21
|a-b|
|a-b|
Imsacred
2012-03-30 19:47:21
|b-a|
|b-a|
Potla
2012-03-30 19:47:21
|a-b|
|a-b|
copeland
2012-03-30 19:47:29
The distance between two complex numbers is the modulus of their difference $|a-b|$.
The distance between two complex numbers is the modulus of their difference $|a-b|$.
copeland
2012-03-30 19:47:42
The distance between $(1+2i)z^3$ and $z^5$ is \[|(1+2i)z^3-z^5|.\]
The distance between $(1+2i)z^3$ and $z^5$ is \[|(1+2i)z^3-z^5|.\]
copeland
2012-03-30 19:47:45
Do you see an easy way to simplify this?
Do you see an easy way to simplify this?
mathswimmer
2012-03-30 19:48:14
z^3 pops otu
z^3 pops otu
lucylai
2012-03-30 19:48:14
factor out z^3
factor out z^3
lazorpenguin27143
2012-03-30 19:48:14
factor out |z^3|
factor out |z^3|
Hydroxide
2012-03-30 19:48:14
factor out the z^3
factor out the z^3
admin25
2012-03-30 19:48:14
We can factor out a $ z^3 $
We can factor out a $ z^3 $
kmc927
2012-03-30 19:48:14
factor a z^3
factor a z^3
centralbs
2012-03-30 19:48:14
Factor out a abs (z^3)
Factor out a abs (z^3)
copeland
2012-03-30 19:48:20
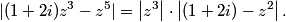
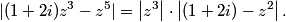
copeland
2012-03-30 19:48:25
Can we simplify this quantity further?
Can we simplify this quantity further?
shreyash
2012-03-30 19:49:06
Factor out the magnitude of z^3 which is 125
Factor out the magnitude of z^3 which is 125
brokenfixer
2012-03-30 19:49:06
|z^3| is known
|z^3| is known
matholympiad25
2012-03-30 19:49:06
Yes |z^3|=125
Yes |z^3|=125
shreyash
2012-03-30 19:49:06
Magnitude of z^3 is 5^3 = 125
Magnitude of z^3 is 5^3 = 125
lucylai
2012-03-30 19:49:06
|z^3|=|z|^3=125
|z^3|=|z|^3=125
nmandi7
2012-03-30 19:49:06
125
125
TeamJacob
2012-03-30 19:49:06
magnitude of z^3 is 5^3
magnitude of z^3 is 5^3
Hydroxide
2012-03-30 19:49:06
|z^3|=|z|^3=5^3=125
|z^3|=|z|^3=5^3=125
nmandi7
2012-03-30 19:49:08
mag of z^3 = 125
mag of z^3 = 125
copeland
2012-03-30 19:49:14
We know that $|z|=5$ and since $|z^3|=|z|^3=125$, we can say \[|(1+2i)z^3-z^5|=125|(1+2i)-z^2|.\]
We know that $|z|=5$ and since $|z^3|=|z|^3=125$, we can say \[|(1+2i)z^3-z^5|=125|(1+2i)-z^2|.\]
copeland
2012-03-30 19:49:17
Now we want to maximize this value. Specifically we want to find the point $z^2$ such that $|z^2|=25$ and $z^2$ is as far away as possible from the point $1+2i$.
Now we want to maximize this value. Specifically we want to find the point $z^2$ such that $|z^2|=25$ and $z^2$ is as far away as possible from the point $1+2i$.
copeland
2012-03-30 19:49:26
What is the set $|u|=25$, where $u$ is a complex number?
What is the set $|u|=25$, where $u$ is a complex number?
himym83
2012-03-30 19:49:55
the circle of radius 25
the circle of radius 25
danielguo94
2012-03-30 19:49:55
circle w/ center at origin and radius 25
circle w/ center at origin and radius 25
sonchecky
2012-03-30 19:49:55
A circle with radius 25 centered around the point 0+0i
A circle with radius 25 centered around the point 0+0i
lucylai
2012-03-30 19:49:55
circle of radius 25 centered on origin
circle of radius 25 centered on origin
nackster12
2012-03-30 19:49:55
the circle with radius 25 centered at the origin
the circle with radius 25 centered at the origin
heliootrope
2012-03-30 19:49:55
A circle centered at the origin with radius 25
A circle centered at the origin with radius 25
copeland
2012-03-30 19:49:59
This set is a circle of radius 25 centered at the origin.
This set is a circle of radius 25 centered at the origin.
copeland
2012-03-30 19:50:03

copeland
2012-03-30 19:50:05
What point on the circle is farthest from the given point?
What point on the circle is farthest from the given point?
brokenfixer
2012-03-30 19:50:55
make sure that z^2 points opposite to (1+2i) ... z^2 = - C * (1+2i) where C real >0
make sure that z^2 points opposite to (1+2i) ... z^2 = - C * (1+2i) where C real >0
theone142857
2012-03-30 19:50:55
line through 1+2i and origin hits circle lz^2l=25 in third quadrant. That's z
line through 1+2i and origin hits circle lz^2l=25 in third quadrant. That's z
ptes77
2012-03-30 19:50:55
the diameter
the diameter
adamdai97
2012-03-30 19:50:55
oppostite on the diameter
oppostite on the diameter
admin25
2012-03-30 19:50:55
If you draw a diameter through the point, it's the point where the diameter intersects the circle
If you draw a diameter through the point, it's the point where the diameter intersects the circle
claudiafeng
2012-03-30 19:50:55
The point farther from 1+2i on the diameter that contains 1+2i.
The point farther from 1+2i on the diameter that contains 1+2i.
ptes77
2012-03-30 19:50:55
the point on the opposite side in quadrant III
the point on the opposite side in quadrant III
AbsoluteFriend
2012-03-30 19:50:55
A point on the circumference in the lower left.
A point on the circumference in the lower left.
trident
2012-03-30 19:50:55
point where the diameter through 1 + 2i hits the circle
point where the diameter through 1 + 2i hits the circle
copeland
2012-03-30 19:50:59
The distance is maximized at the antipodal point:
The distance is maximized at the antipodal point:
copeland
2012-03-30 19:51:04

copeland
2012-03-30 19:51:12
Incidentally, the synthetic way to show that this point is farthest is by drawing (in blue below) the circle with center $1+2i$ that contains the antipodal point. By symmetry the two circles must be tangent, so every other point on the black circle is closer than this point of tangency.
Incidentally, the synthetic way to show that this point is farthest is by drawing (in blue below) the circle with center $1+2i$ that contains the antipodal point. By symmetry the two circles must be tangent, so every other point on the black circle is closer than this point of tangency.
copeland
2012-03-30 19:51:17
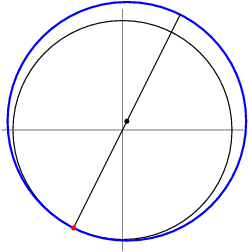

copeland
2012-03-30 19:51:32
Now how does this help us write $z^2$?
Now how does this help us write $z^2$?
brokenfixer
2012-03-30 19:52:39
-(1+2i)*25 / |1+2i|
-(1+2i)*25 / |1+2i|
googol.plex
2012-03-30 19:52:39
we know the slope of the line and the length of the line
we know the slope of the line and the length of the line
mathswimmer
2012-03-30 19:52:39
x^2+(2x)^2=25^2
x^2+(2x)^2=25^2
nackster12
2012-03-30 19:52:39
we can find that point by coordinate bashing?
we can find that point by coordinate bashing?
copeland
2012-03-30 19:52:46
That's a lot of fancy ideas.
That's a lot of fancy ideas.
copeland
2012-03-30 19:53:14
What do we KNOW about this point? How is it related to 1+2i?
What do we KNOW about this point? How is it related to 1+2i?
matholympiad25
2012-03-30 19:53:57
it is a real number * (1+2i)
it is a real number * (1+2i)
heliootrope
2012-03-30 19:53:57
a and b have the same ratio?
a and b have the same ratio?
m1sterzer0
2012-03-30 19:53:57
on the line through 0 and 1+2i
on the line through 0 and 1+2i
admin25
2012-03-30 19:53:57
the ratio of the imaginary part to the real part is the same, since it's on the same line through the origin
the ratio of the imaginary part to the real part is the same, since it's on the same line through the origin
nackster12
2012-03-30 19:53:57
the real part is half of the imaginary part
the real part is half of the imaginary part
TeamJacob
2012-03-30 19:53:57
the coefficients are proportional
the coefficients are proportional
shreyash
2012-03-30 19:53:57
-1 - 2i
-1 - 2i
joshxiong
2012-03-30 19:53:57
b=2a
b=2a
copeland
2012-03-30 19:54:03
We know that $z^2$ has to be a positive multiple of $-1-2i$. We also know that $|z^2|=|z|^2=25.$ What is $z^2$?
We know that $z^2$ has to be a positive multiple of $-1-2i$. We also know that $|z^2|=|z|^2=25.$ What is $z^2$?
GeorgiaTechMan
2012-03-30 19:55:00
5sqrt5(-1-2i)
5sqrt5(-1-2i)
iamthygod!!!!!!
2012-03-30 19:55:00
-25/(sqrt5)
-25/(sqrt5)
iamthygod!!!!!!
2012-03-30 19:55:00
(-25/root5)*(1+2i)
(-25/root5)*(1+2i)
matholympiad25
2012-03-30 19:55:00
-sqrt(125) - sqrt(500) * i
-sqrt(125) - sqrt(500) * i
lazorpenguin27143
2012-03-30 19:55:00
$ z^{2}=-5\sqrt{5}-10\sqrt{5}i $
$ z^{2}=-5\sqrt{5}-10\sqrt{5}i $
sonchecky
2012-03-30 19:55:00
(-1-2i)(25/sqrt(5)) = -5sqrt(5) - 10sqrt(5)i
(-1-2i)(25/sqrt(5)) = -5sqrt(5) - 10sqrt(5)i
brokenfixer
2012-03-30 19:55:00
-5sqrt(5) -10sqrt(5) i
-5sqrt(5) -10sqrt(5) i
m1sterzer0
2012-03-30 19:55:07
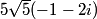
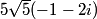
copeland
2012-03-30 19:55:08
Since $|-1-2i|=\sqrt{1^2+2^2}=\sqrt5$, We need $z^2=(5\sqrt5)(-1-2i)$. As a check, this does indeed give us \[|z^2|=|(5\sqrt5)(-1-2i)|=5\sqrt5|-1-2i|=25.\]
Since $|-1-2i|=\sqrt{1^2+2^2}=\sqrt5$, We need $z^2=(5\sqrt5)(-1-2i)$. As a check, this does indeed give us \[|z^2|=|(5\sqrt5)(-1-2i)|=5\sqrt5|-1-2i|=25.\]
copeland
2012-03-30 19:55:12
Now what is $z^4$?
Now what is $z^4$?
lazorpenguin27143
2012-03-30 19:56:08
$ z^{4}=-375+500i $
$ z^{4}=-375+500i $
Duncanyang
2012-03-30 19:56:08
125(-3+4i)
125(-3+4i)
brokenfixer
2012-03-30 19:56:08
125(-3+4i)
125(-3+4i)
alex31415
2012-03-30 19:56:08
-375+500i?
-375+500i?
Duncanyang
2012-03-30 19:56:08
-375+500i
-375+500i
copeland
2012-03-30 19:57:02
Squaring $z^2$ gives us
\begin{align*}
z^4&=(z^2)^2\\
&=(5\sqrt5)^2(-1-2i)^2\\
&=125(1+2i)^2\\
&=125(1+4i-4)\\
&=-375+500i.
\end{align*}
Squaring $z^2$ gives us
\begin{align*}
z^4&=(z^2)^2\\
&=(5\sqrt5)^2(-1-2i)^2\\
&=125(1+2i)^2\\
&=125(1+4i-4)\\
&=-375+500i.
\end{align*}
copeland
2012-03-30 19:57:07
What does that give us for the solution?
What does that give us for the solution?
matholympiad25
2012-03-30 19:57:30
-375+500i, c+d = 125
-375+500i, c+d = 125
kmc927
2012-03-30 19:57:30
125
125
himym83
2012-03-30 19:57:30
500-375=125
500-375=125
lucylai
2012-03-30 19:57:30
125
125
19oshawott98
2012-03-30 19:57:30
125
125
Voytek
2012-03-30 19:57:30
125
125
centralbs
2012-03-30 19:57:30
125
125
ptes77
2012-03-30 19:57:30
125
125
ahaanomegas
2012-03-30 19:57:30
500 - 375 = 125.
500 - 375 = 125.
n2010Math
2012-03-30 19:57:30
125
125
jasonmathcounts
2012-03-30 19:57:30
125
125
ytao
2012-03-30 19:57:30
500+(-375)=125
500+(-375)=125
lucylai
2012-03-30 19:57:30
125
125
ABCDE
2012-03-30 19:57:30
125
125
claudiafeng
2012-03-30 19:57:30
125
125
CantonMathGuy
2012-03-30 19:57:30
125
125
Hydroxide
2012-03-30 19:57:30
-375+500=125
-375+500=125
copeland
2012-03-30 19:57:32
$500+(-375)=\boxed{125}$.
$500+(-375)=\boxed{125}$.
nackster12
2012-03-30 19:57:49
why were we given b>0? did we use that at all?
why were we given b>0? did we use that at all?
copeland
2012-03-30 19:57:52
Good question.
Good question.
copeland
2012-03-30 19:58:03
We never needed to find $z$ to solve this problem.
We never needed to find $z$ to solve this problem.
copeland
2012-03-30 19:58:33
In fact there are TWO possibilities for $z$ that solve this problem and that restriction narrows it down to a unique value.
In fact there are TWO possibilities for $z$ that solve this problem and that restriction narrows it down to a unique value.
copeland
2012-03-30 19:58:56
7. Let $S$ be the increasing sequence of positive integers whose binary representation has exactly 8 ones. Let $N$ be the 1000th number in $S$. Find the remainder when $N$ is divided by 1000.
7. Let $S$ be the increasing sequence of positive integers whose binary representation has exactly 8 ones. Let $N$ be the 1000th number in $S$. Find the remainder when $N$ is divided by 1000.
copeland
2012-03-30 19:59:11
What information might be useful to know?
What information might be useful to know?
lucylai
2012-03-30 20:00:08
how many zeros N has
how many zeros N has
CantonMathGuy
2012-03-30 20:00:08
the number on numbers with a number of zeros
the number on numbers with a number of zeros
ytao
2012-03-30 20:00:08
How many 0s
How many 0s
copeland
2012-03-30 20:00:13
We might want to know how many digits are in the number we want.
We might want to know how many digits are in the number we want.
copeland
2012-03-30 20:00:17
How can we determine this?
How can we determine this?
copeland
2012-03-30 20:00:36
How many $k$-digit binary numbers are in $S$?
How many $k$-digit binary numbers are in $S$?
admin25
2012-03-30 20:01:34
$ \binom{k}{8}-\binom{k-1}{8} $
$ \binom{k}{8}-\binom{k-1}{8} $
nackster12
2012-03-30 20:01:34
k-1 choose 7
k-1 choose 7
alex31415
2012-03-30 20:01:34
(k-1)C7?
(k-1)C7?
copeland
2012-03-30 20:01:39
The first digit of any number has to be a 1, so the remaining $k-1$ digits consist of 7 ones and $k-8$ zeroes.
The first digit of any number has to be a 1, so the remaining $k-1$ digits consist of 7 ones and $k-8$ zeroes.
copeland
2012-03-30 20:01:46
So there are $\dbinom{k-1}{7}$ such numbers.
So there are $\dbinom{k-1}{7}$ such numbers.
copeland
2012-03-30 20:01:51
That is, there are:
\begin{align*}
\tbinom77 & \text{8-digit numbers}\\
\tbinom87 & \text{9-digit numbers}\\
\tbinom97 & \text{10-digit numbers}\\
\end{align*}
etc.
That is, there are:
\begin{align*}
\tbinom77 & \text{8-digit numbers}\\
\tbinom87 & \text{9-digit numbers}\\
\tbinom97 & \text{10-digit numbers}\\
\end{align*}
etc.
copeland
2012-03-30 20:01:58
How do we use this information? I don't want to compute all those numbers if I don't have to.
How do we use this information? I don't want to compute all those numbers if I don't have to.
copeland
2012-03-30 20:02:40
If we sum them, what do we get?
If we sum them, what do we get?
himym83
2012-03-30 20:02:46
hockey stick identity
hockey stick identity
alex31415
2012-03-30 20:02:46
Hockey Stick Identity
Hockey Stick Identity
flyrain
2012-03-30 20:02:46
hockey stick identity
hockey stick identity
joshxiong
2012-03-30 20:02:46
Hockey stick identity.
Hockey stick identity.
admin25
2012-03-30 20:02:46
Hockey stick identity!
Hockey stick identity!
lucylai
2012-03-30 20:02:46
hockey stick rule
hockey stick rule
ahaanomegas
2012-03-30 20:02:46
Is this the Hockey Stick Identity?
Is this the Hockey Stick Identity?
copeland
2012-03-30 20:02:49
We can use the Hockey Stick Identity!
We can use the Hockey Stick Identity!
copeland
2012-03-30 20:02:59
\[\binom77 + \binom87 + \cdots + \binom{n}{7} = \binom{n+1}{8}.\]
\[\binom77 + \binom87 + \cdots + \binom{n}{7} = \binom{n+1}{8}.\]
copeland
2012-03-30 20:03:04
What does this mean for us?
What does this mean for us?
alex31415
2012-03-30 20:03:47
You could put beginning 0's, so 10101 would be 010101, or 0010101, etc.
You could put beginning 0's, so 10101 would be 010101, or 0010101, etc.
copeland
2012-03-30 20:03:51
It means that there are $\binom{k}{8}$ numbers in $S$ with $k$ digits or less.
It means that there are $\binom{k}{8}$ numbers in $S$ with $k$ digits or less.
copeland
2012-03-30 20:03:56
We actually could have seen this directly: think of arranging 8 ones and $k-8$ zeroes, where we allow leading zeroes. (This illustrates a nice rule of thumb: whenever you find yourself using the Hockey Stick Identity, there's a really good chance you're doing things the hard way.)
We actually could have seen this directly: think of arranging 8 ones and $k-8$ zeroes, where we allow leading zeroes. (This illustrates a nice rule of thumb: whenever you find yourself using the Hockey Stick Identity, there's a really good chance you're doing things the hard way.)
himym83
2012-03-30 20:04:20
(n+1)C8 > 1000
(n+1)C8 > 1000
Hydroxide
2012-03-30 20:04:20
find smallest such that n+1C 8>1000
find smallest such that n+1C 8>1000
mathswimmer
2012-03-30 20:04:20
first n such that it is greater than 1000, that is the number of digits
first n such that it is greater than 1000, that is the number of digits
flyrain
2012-03-30 20:04:20
solve n when n+1 choose 8 is 1000
solve n when n+1 choose 8 is 1000
ptes77
2012-03-30 20:04:20
we find the least n that it will be over 1000
we find the least n that it will be over 1000
wmcho1007
2012-03-30 20:04:20
we find the largest n+1 such that c(n+1,8) is less than 1000
we find the largest n+1 such that c(n+1,8) is less than 1000
claudiafeng
2012-03-30 20:04:20
We need to find when (n+1)C8 is greater/equal to 1000?
We need to find when (n+1)C8 is greater/equal to 1000?
copeland
2012-03-30 20:04:24
Now we can test some values of $k.$
Now we can test some values of $k.$
copeland
2012-03-30 20:04:27
A little experimentation gives us\[\binom{12}{8} = 495\]and\[\binom{13}{8} = 1287.\]
A little experimentation gives us\[\binom{12}{8} = 495\]and\[\binom{13}{8} = 1287.\]
copeland
2012-03-30 20:04:33
So what can we conclude?
So what can we conclude?
awesomemathlete
2012-03-30 20:05:06
13 digits
13 digits
nmandi7
2012-03-30 20:05:06
13 digit
13 digit
TigerSneak1
2012-03-30 20:05:06
the number has 13 digits
the number has 13 digits
Larklight
2012-03-30 20:05:06
13 digits
13 digits
ABCDE
2012-03-30 20:05:06
N is a 13 digit binary number
N is a 13 digit binary number
nmandi7
2012-03-30 20:05:06
k is 13 digit #
k is 13 digit #
proglote
2012-03-30 20:05:06
the 1000th number has 13 digits
the 1000th number has 13 digits
trident
2012-03-30 20:05:06
the 1000th number has 13 digits
the 1000th number has 13 digits
copeland
2012-03-30 20:05:10
The number we want (the 1000th number in $S$) is a 13-digit number.
The number we want (the 1000th number in $S$) is a 13-digit number.
copeland
2012-03-30 20:05:13
Is there something stronger we can say?
Is there something stronger we can say?
googol.plex
2012-03-30 20:05:54
so it's the 505th number with 13 digits.
so it's the 505th number with 13 digits.
shreyash
2012-03-30 20:05:54
It is the 505th number with 13 digits
It is the 505th number with 13 digits
brokenfixer
2012-03-30 20:05:54
it is the 505th?
it is the 505th?
lucylai
2012-03-30 20:05:54
it's the 505th 13 digit number with 8 ones
it's the 505th 13 digit number with 8 ones
Imsacred
2012-03-30 20:05:54
it is the 505th 13 digit number
it is the 505th 13 digit number
nmandi7
2012-03-30 20:05:54
505th
505th
copeland
2012-03-30 20:05:58
The number we want is the 1000-495 = 505th 13-digit number in $S.$
The number we want is the 1000-495 = 505th 13-digit number in $S.$
copeland
2012-03-30 20:06:02
This number is the digit 1 placed in front of the 505th largest number with 7 ones and 5 zeroes.
This number is the digit 1 placed in front of the 505th largest number with 7 ones and 5 zeroes.
copeland
2012-03-30 20:06:07
Now the problem becomes a matter of careful counting and bookkeeping.
Now the problem becomes a matter of careful counting and bookkeeping.
copeland
2012-03-30 20:06:09
What next?
What next?
alex31415
2012-03-30 20:06:55
Apply that to every digit?
Apply that to every digit?
mathswimmer
2012-03-30 20:06:55
if the 12th digit is 0, see if filling in the remaining 11 is enough to get up to 505. if not, then the 12th digit is 1. continue in this manner
if the 12th digit is 0, see if filling in the remaining 11 is enough to get up to 505. if not, then the 12th digit is 1. continue in this manner
proglote
2012-03-30 20:06:55
consider the second digit
consider the second digit
nmandi7
2012-03-30 20:06:55
split it into lower combinations
split it into lower combinations
wmcho1007
2012-03-30 20:06:57
determine if the second digit is a 1 or a 0
determine if the second digit is a 1 or a 0
copeland
2012-03-30 20:07:07
We can determine if the 2nd digit (from the left) is a 0 or 1.
We can determine if the 2nd digit (from the left) is a 0 or 1.
copeland
2012-03-30 20:07:13
The 13-digit numbers in $S$ consist of all the 13-digit numbers in S starting with 10, followed by all the 13-digit numbers in $S$ starting with 11.
The 13-digit numbers in $S$ consist of all the 13-digit numbers in S starting with 10, followed by all the 13-digit numbers in $S$ starting with 11.
copeland
2012-03-30 20:07:16
How many numbers in the former group: that start with 10?
How many numbers in the former group: that start with 10?
mathswimmer
2012-03-30 20:08:26
11C7
11C7
Seedleaf
2012-03-30 20:08:26
330
330
admin25
2012-03-30 20:08:26
$ \binom{11}{7} $
$ \binom{11}{7} $
wmcho1007
2012-03-30 20:08:26
C(11,7)=330
C(11,7)=330
nackster12
2012-03-30 20:08:26
11 choose 7=330
11 choose 7=330
kmc927
2012-03-30 20:08:26
330
330
heliootrope
2012-03-30 20:08:26
11 choose 7
11 choose 7
iamthygod!!!!!!
2012-03-30 20:08:26
330
330
copeland
2012-03-30 20:08:32
Thus there are $\dbinom{11}{4} = 330$ such numbers.
Thus there are $\dbinom{11}{4} = 330$ such numbers.
copeland
2012-03-30 20:08:35
So since we wanted the 505th 13-digit number, we first have to exhaust the 330 13-digit numbers starting with 10.
So since we wanted the 505th 13-digit number, we first have to exhaust the 330 13-digit numbers starting with 10.
copeland
2012-03-30 20:08:41
Then we want the 505-330 = 175th 13-digit number starting with 11.
Then we want the 505-330 = 175th 13-digit number starting with 11.
copeland
2012-03-30 20:08:46
Now what?
Now what?
nackster12
2012-03-30 20:09:20
find the third digit
find the third digit
himym83
2012-03-30 20:09:20
do the same thing for the next digit
do the same thing for the next digit
lucylai
2012-03-30 20:09:20
find numbers starting with 110
find numbers starting with 110
coldsummer
2012-03-30 20:09:20
110 or 111
110 or 111
deepankar
2012-03-30 20:09:20
break into start with 110 or 111
break into start with 110 or 111
eccfcco15
2012-03-30 20:09:20
repeat the above process to get the next digit
repeat the above process to get the next digit
mathnerd101
2012-03-30 20:09:20
find the 3rd digit?
find the 3rd digit?
copeland
2012-03-30 20:09:27
Ugh, really?
Ugh, really?
copeland
2012-03-30 20:09:28
OK.
OK.
copeland
2012-03-30 20:09:32
Again, we split our group into 13-digit numbers starting with 110 and 13-digit numbers starting with 111.
Again, we split our group into 13-digit numbers starting with 110 and 13-digit numbers starting with 111.
copeland
2012-03-30 20:09:35
How many of the former: 13-digit numbers starting with 110?
How many of the former: 13-digit numbers starting with 110?
admin25
2012-03-30 20:10:16
There are $ \binom{10}{6} $ numbers that begin with 110
There are $ \binom{10}{6} $ numbers that begin with 110
joshxiong
2012-03-30 20:10:16
210.
210.
claudiafeng
2012-03-30 20:10:16
10C6
10C6
wmcho1007
2012-03-30 20:10:16
C(10,6)=210
C(10,6)=210
googol.plex
2012-03-30 20:10:16
10C4
10C4
lucylai
2012-03-30 20:10:16
C(10, 4)=210
C(10, 4)=210
iamthygod!!!!!!
2012-03-30 20:10:16
210?
210?
copeland
2012-03-30 20:10:20
There are 6 ones and 4 zeroes to place, so there are $\dbinom{10}{4} = 210$ of them.
There are 6 ones and 4 zeroes to place, so there are $\dbinom{10}{4} = 210$ of them.
copeland
2012-03-30 20:10:24
Since we only want the 175th 13-digit number starting with 11, we know it will also be the 175th 13-digit number among the 210 starting with 110.
Since we only want the 175th 13-digit number starting with 11, we know it will also be the 175th 13-digit number among the 210 starting with 110.
fredgauss
2012-03-30 20:10:41
is this the easiest way to do this?
is this the easiest way to do this?
copeland
2012-03-30 20:10:42
Trust me. If I knew a better answer we would NOT be doing this.
Trust me. If I knew a better answer we would NOT be doing this.
copeland
2012-03-30 20:10:46
So now we want the 175th 13-digit number in $S$ starting with 110.
So now we want the 175th 13-digit number in $S$ starting with 110.
copeland
2012-03-30 20:10:55
Now what?
Now what?
coldsummer
2012-03-30 20:11:19
1100 or 1101?
1100 or 1101?
ptes77
2012-03-30 20:11:19
do the same to the 4th digit
do the same to the 4th digit
shreyash
2012-03-30 20:11:19
Find the 4th digit
Find the 4th digit
wmcho1007
2012-03-30 20:11:19
the fourth digit......
the fourth digit......
eccfcco15
2012-03-30 20:11:19
continue
continue
claudiafeng
2012-03-30 20:11:19
Break it.. further..
Break it.. further..
nmandi7
2012-03-30 20:11:19
do the next digit ... ugh
do the next digit ... ugh
sonchecky
2012-03-30 20:11:19
consider all 13-digit numbers starting with 1100
consider all 13-digit numbers starting with 1100
copeland
2012-03-30 20:11:23
Same game: consider numbers starting with 1100 and numbers starting with 1101. How many of the former?
Same game: consider numbers starting with 1100 and numbers starting with 1101. How many of the former?
-Transcend-
2012-03-30 20:12:14
9C3
9C3
claudiafeng
2012-03-30 20:12:14
9C5
9C5
joshxiong
2012-03-30 20:12:14
84.
84.
kmc927
2012-03-30 20:12:14
84
84
coldsummer
2012-03-30 20:12:14
9C6
9C6
Seedleaf
2012-03-30 20:12:14
9C6 = 84
9C6 = 84
lucylai
2012-03-30 20:12:14
C(9, 3)=84
C(9, 3)=84
deepankar
2012-03-30 20:12:14
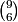
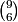
nackster12
2012-03-30 20:12:14
9C6=84
9C6=84
copeland
2012-03-30 20:12:18
We have 6 ones and 3 zeroes remaining, so there are $\binom93 = 84$ of them.
We have 6 ones and 3 zeroes remaining, so there are $\binom93 = 84$ of them.
copeland
2012-03-30 20:12:21
That means we want the 175 - 84 = 91st 13-digit number in $S$ starting with 1101.
That means we want the 175 - 84 = 91st 13-digit number in $S$ starting with 1101.
copeland
2012-03-30 20:12:30
And again: split into numbers beginning with 11010 and 11011. How many of the former?
And again: split into numbers beginning with 11010 and 11011. How many of the former?
sonchecky
2012-03-30 20:12:53
8 choose 3 = 56
8 choose 3 = 56
Duncanyang
2012-03-30 20:12:53
8 choose 5
8 choose 5
claudiafeng
2012-03-30 20:12:53
8C5=56
8C5=56
Relativity1618
2012-03-30 20:12:53
8C3
8C3
kmc927
2012-03-30 20:12:53
56
56
coldsummer
2012-03-30 20:12:53
therefore we do it again.......8C5, or 56
therefore we do it again.......8C5, or 56
copeland
2012-03-30 20:12:55
We have 5 ones and 3 zeroes remaining, so there are $\binom83 = 56$ of them.
We have 5 ones and 3 zeroes remaining, so there are $\binom83 = 56$ of them.
copeland
2012-03-30 20:12:59
That means we want the 91 - 56 = 35th 13-digit number in $S$ starting with 11011.
That means we want the 91 - 56 = 35th 13-digit number in $S$ starting with 11011.
copeland
2012-03-30 20:13:05
And again(!): split into starting with 110110 and 110111. How many of the former?
And again(!): split into starting with 110110 and 110111. How many of the former?
joshxiong
2012-03-30 20:13:42
35.
35.
flyrain
2012-03-30 20:13:42
110110 7C3
110110 7C3
shreyash
2012-03-30 20:13:42
7C3
7C3
mathnerd101
2012-03-30 20:13:42
7C3
7C3
Mary_Posa
2012-03-30 20:13:42
35
35
sinnoel
2012-03-30 20:13:42
35
35
sonchecky
2012-03-30 20:13:42
7 choose 3 = 35
7 choose 3 = 35
nackster12
2012-03-30 20:13:42
7C3=35
7C3=35
Seedleaf
2012-03-30 20:13:42
7C4 = 35
7C4 = 35
jinguluninja
2012-03-30 20:13:42
35
35
copeland
2012-03-30 20:13:46
We have 4 ones and 3 zeroes remaining, so there are $\binom73 = 35$ of them.
We have 4 ones and 3 zeroes remaining, so there are $\binom73 = 35$ of them.
sinnoel
2012-03-30 20:14:08
yyayyy!
yyayyy!
brokenfixer
2012-03-30 20:14:08
hooray
hooray
copeland
2012-03-30 20:14:12
Aha! We want the 35th such number (beginning with 110110), and there are exactly 35 of them.
Aha! We want the 35th such number (beginning with 110110), and there are exactly 35 of them.
copeland
2012-03-30 20:14:17
So we want the biggest one: the one with all the remaining 1's pushed all the way to the left.
So we want the biggest one: the one with all the remaining 1's pushed all the way to the left.
copeland
2012-03-30 20:14:20
That means that the number we're looking for is 1101101111000.
That means that the number we're looking for is 1101101111000.
copeland
2012-03-30 20:14:25
Now how do we finish?
Now how do we finish?
Relativity1618
2012-03-30 20:15:20
=7032
=7032
sonchecky
2012-03-30 20:15:20
Convert to base 10
Convert to base 10
Imsacred
2012-03-30 20:15:20
base 10!
base 10!
GeorgiaTechMan
2012-03-30 20:15:20
and that is 7032 base ten so our answer is 032!
and that is 7032 base ten so our answer is 032!
joshxiong
2012-03-30 20:15:20
Convert to base 10.
Convert to base 10.
ytao
2012-03-30 20:15:20
Convert to base 10.
Convert to base 10.
sinnoel
2012-03-30 20:15:20
convert to base 10 and add?
convert to base 10 and add?
-Transcend-
2012-03-30 20:15:20
Convert to base 10?
Convert to base 10?
deepankar
2012-03-30 20:15:20
Find base 10 value and divide by 1000
Find base 10 value and divide by 1000
alex31415
2012-03-30 20:15:20
2^3+2^4+2^5+2^6+2^8+2^9+2^11+2^12=7032, so the answer is 032
2^3+2^4+2^5+2^6+2^8+2^9+2^11+2^12=7032, so the answer is 032
thunderPA
2012-03-30 20:15:20
convert it into base ten and divide by 1000
convert it into base ten and divide by 1000
HeatDynasty
2012-03-30 20:15:20
convert it to base 10 number
convert it to base 10 number
19oshawott98
2012-03-30 20:15:26
unencrypt
unencrypt
copeland
2012-03-30 20:15:33
We need the last 3 digits of the base-10 representation of the binary number \[1101101111000.\]
We need the last 3 digits of the base-10 representation of the binary number \[1101101111000.\]
copeland
2012-03-30 20:15:37
This is the last 3 digits of\[8 + 16 + 32 + 64 + 256 + 512 + 2048 + 4096.\]
This is the last 3 digits of\[8 + 16 + 32 + 64 + 256 + 512 + 2048 + 4096.\]
copeland
2012-03-30 20:15:40
Since we can ignore thousands digits, this is just the last three digits of\[8 + 16 + 32 + 64 + 256 + 512 + 48 + 96.\]
Since we can ignore thousands digits, this is just the last three digits of\[8 + 16 + 32 + 64 + 256 + 512 + 48 + 96.\]
copeland
2012-03-30 20:15:43
These numbers sum to 1032, so our answer is $\boxed{032}$.
These numbers sum to 1032, so our answer is $\boxed{032}$.
copeland
2012-03-30 20:16:01
I notice that nobody said 7 when I asked what your favorite problems were. . .
I notice that nobody said 7 when I asked what your favorite problems were. . .
lucylai
2012-03-30 20:16:28
i did
i did
copeland
2012-03-30 20:16:37
Oh, there was one vote.
Oh, there was one vote.
copeland
2012-03-30 20:16:44
Yay. Love for #7.
Yay. Love for #7.
copeland
2012-03-30 20:16:45
8. The complex numbers $z$ and $w$ satisfy the system
\begin{align*}
z + \frac{20i}{w} &= 5 + i \\
w + \frac{12i}{z} &= -4 + 10i.
\end{align*}
Find the smallest possible value of $|zw|^2$.
8. The complex numbers $z$ and $w$ satisfy the system
\begin{align*}
z + \frac{20i}{w} &= 5 + i \\
w + \frac{12i}{z} &= -4 + 10i.
\end{align*}
Find the smallest possible value of $|zw|^2$.
mathnerd101
2012-03-30 20:17:11
ugh complex numbers
ugh complex numbers
copeland
2012-03-30 20:17:12
"Woohoo complex numbers!" you mean?
"Woohoo complex numbers!" you mean?
copeland
2012-03-30 20:17:13
How can we get something manageable from these equations?
How can we get something manageable from these equations?
Relativity1618
2012-03-30 20:17:33
multiply both equations
multiply both equations
claudiafeng
2012-03-30 20:17:33
Multiply the equations
Multiply the equations
theone142857
2012-03-30 20:17:33
mutiply them together
mutiply them together
proglote
2012-03-30 20:17:33
multiply the two equations
multiply the two equations
himym83
2012-03-30 20:17:33
multiply the equations together
multiply the equations together
jinguluninja
2012-03-30 20:17:33
multiply them
multiply them
sonchecky
2012-03-30 20:17:33
Multiply them together
Multiply them together
ABCDE
2012-03-30 20:17:33
multiply them
multiply them
zinko1991
2012-03-30 20:17:33
multiply them?
multiply them?
CantonMathGuy
2012-03-30 20:17:33
multiply!
multiply!
GeorgiaTechMan
2012-03-30 20:17:33
multiply!
multiply!
esque
2012-03-30 20:17:39
multiply them together~~~~
multiply them together~~~~
copeland
2012-03-30 20:17:41
Notice that if we take the product on the left side the cross-terms are going to be constants:\[\left(z+\frac{20i}w\right)\left(w+\frac{12i}z\right)=zw+20i\frac ww+12i\frac zz+\frac{20i\cdot12i}{wz}.\]
Notice that if we take the product on the left side the cross-terms are going to be constants:\[\left(z+\frac{20i}w\right)\left(w+\frac{12i}z\right)=zw+20i\frac ww+12i\frac zz+\frac{20i\cdot12i}{wz}.\]
copeland
2012-03-30 20:17:49
Therefore if we multiply these equations, left-by-left and right-by-right, we get \[zw+32i-\frac{240}{wz}=(5+i)(-4+10i)=-20-4i+50i-10=-30+46i.\]
Therefore if we multiply these equations, left-by-left and right-by-right, we get \[zw+32i-\frac{240}{wz}=(5+i)(-4+10i)=-20-4i+50i-10=-30+46i.\]
copeland
2012-03-30 20:17:58
We notice that $zw$ cannot be zero or the original system is not well-defined.
We notice that $zw$ cannot be zero or the original system is not well-defined.
copeland
2012-03-30 20:18:06
Multiplying this equation by $zw$ and simplifying gives us\[(zw)^2+(30-14i)(zw)-240=0.\]
Multiplying this equation by $zw$ and simplifying gives us\[(zw)^2+(30-14i)(zw)-240=0.\]
copeland
2012-03-30 20:18:14
This polynomial has two roots. How do we find them?
This polynomial has two roots. How do we find them?
Relativity1618
2012-03-30 20:18:41
quadratic formula
quadratic formula
ABCDE
2012-03-30 20:18:41
quadratic formula
quadratic formula
lucylai
2012-03-30 20:18:41
quadratic formula
quadratic formula
Xcellence
2012-03-30 20:18:41
vietas formulas
vietas formulas
Duncanyang
2012-03-30 20:18:41
quadratic formulae!!!
quadratic formulae!!!
coldsummer
2012-03-30 20:18:41
quadratic formula?
quadratic formula?
Hydroxide
2012-03-30 20:18:41
quadratoc formula
quadratoc formula
shreyash
2012-03-30 20:18:41
Quadratic equation
Quadratic equation
admin25
2012-03-30 20:18:41
Vietas?
Vietas?
nmandi7
2012-03-30 20:18:41
quadratic formula
quadratic formula
googol.plex
2012-03-30 20:18:41
we use quadratic formula
we use quadratic formula
adamdai97
2012-03-30 20:18:41
quadratic formula?
quadratic formula?
Seedleaf
2012-03-30 20:18:41
quadratic formula?
quadratic formula?
copeland
2012-03-30 20:18:45
The roots are actually guessable if you're really lucky (noticing that the product of the roots is real and negative is a big hint). The quadratic formula is probably the fastest way to go, though.
The roots are actually guessable if you're really lucky (noticing that the product of the roots is real and negative is a big hint). The quadratic formula is probably the fastest way to go, though.
copeland
2012-03-30 20:18:53
By the quadratic formula we must have \[zw=\frac{-30+14i\pm\sqrt{(30-14i)^2+4\cdot240}}2,\]which simplifies to \[zw=-15+7i\pm\sqrt{416-210i}.\]
By the quadratic formula we must have \[zw=\frac{-30+14i\pm\sqrt{(30-14i)^2+4\cdot240}}2,\]which simplifies to \[zw=-15+7i\pm\sqrt{416-210i}.\]
copeland
2012-03-30 20:19:02
Yuck. We need a square root, $a+bi=\sqrt{416-210i}$. We can find this square root by squaring, $(a+bi)^2=416-210i$.
Yuck. We need a square root, $a+bi=\sqrt{416-210i}$. We can find this square root by squaring, $(a+bi)^2=416-210i$.
copeland
2012-03-30 20:19:13
Expanding this and equating the real and imaginary parts tells us we want to solve
\begin{align*}
a^2-b^2&=416\\
2ab&=-210.
\end{align*}
Expanding this and equating the real and imaginary parts tells us we want to solve
\begin{align*}
a^2-b^2&=416\\
2ab&=-210.
\end{align*}
copeland
2012-03-30 20:19:26
Do you see the solutions?
Do you see the solutions?
copeland
2012-03-30 20:20:15
Check your answers! You don't want to be losing points on sign errors!
Check your answers! You don't want to be losing points on sign errors!
himym83
2012-03-30 20:20:46
21 and -5
21 and -5
esque
2012-03-30 20:20:46
a=-21, b=5 or a=21, b=-5
a=-21, b=5 or a=21, b=-5
ABCDE
2012-03-30 20:20:46
a=21 and b=-5
a=21 and b=-5
claudiafeng
2012-03-30 20:20:46
$(\pm 21, \mp 5)$
$(\pm 21, \mp 5)$
theone142857
2012-03-30 20:20:46
21 and -5
21 and -5
admin25
2012-03-30 20:20:46
(a,b)=(21,-5) or (-21,5)
(a,b)=(21,-5) or (-21,5)
vjnmath
2012-03-30 20:20:46
21 and -5
21 and -5
ABCDE
2012-03-30 20:20:46
a=21 and b=-5
a=21 and b=-5
-Transcend-
2012-03-30 20:20:46
(a, b) = (21, -5)
(a, b) = (21, -5)
karatemagic7
2012-03-30 20:20:46
a=21, b=-5 or a=-21, b=5
a=21, b=-5 or a=-21, b=5
nackster12
2012-03-30 20:20:46
(21, -5) or (-21,5)
(21, -5) or (-21,5)
alex31415
2012-03-30 20:20:46
-21,5?
-21,5?
ThEeLiTePaRk
2012-03-30 20:20:46
21 and -5 :D
21 and -5 :D
copeland
2012-03-30 20:20:52
Since $a^2>416$, we know that $a$ must be a factor of 105 and that $|a|$ must also be at least 20. That narrows things down a lot. Indeed we have to have $a=\pm21$ or $a=\pm35$ or $a=\pm105$.
Since $a^2>416$, we know that $a$ must be a factor of 105 and that $|a|$ must also be at least 20. That narrows things down a lot. Indeed we have to have $a=\pm21$ or $a=\pm35$ or $a=\pm105$.
copeland
2012-03-30 20:21:02
Checking we find that $21^2-416=441-416=25=5^2$, so indeed $a=\pm21$ and $b=\pm5$.
Checking we find that $21^2-416=441-416=25=5^2$, so indeed $a=\pm21$ and $b=\pm5$.
copeland
2012-03-30 20:21:10
Since $ab$ is negative, the square roots of $416-210i$ are $\pm(21-5i).$
Since $ab$ is negative, the square roots of $416-210i$ are $\pm(21-5i).$
copeland
2012-03-30 20:21:16
Therefore $zw=-15+7i\pm(21-5i)$, so $zw=6+2i$ or $zw=-36+12i$.
Therefore $zw=-15+7i\pm(21-5i)$, so $zw=6+2i$ or $zw=-36+12i$.
copeland
2012-03-30 20:21:20
What is the minimum value for $|zw|^2$?
What is the minimum value for $|zw|^2$?
copeland
2012-03-30 20:22:07
I'll give you a hint: This is an AIME problem. The answer is probably at least real.
I'll give you a hint: This is an AIME problem. The answer is probably at least real.
sinnoel
2012-03-30 20:22:19
040!
040!
wmcho1007
2012-03-30 20:22:19
therefore its 40?
therefore its 40?
GeorgiaTechMan
2012-03-30 20:22:19
6^2+2^2=040
6^2+2^2=040
karatemagic7
2012-03-30 20:22:19
6^2+2^2=40
6^2+2^2=40
Hydroxide
2012-03-30 20:22:19
40
40
brokenfixer
2012-03-30 20:22:19
040
040
admin25
2012-03-30 20:22:19
$ 6^2+2^2=\boxed{040} $
$ 6^2+2^2=\boxed{040} $
Seedleaf
2012-03-30 20:22:19
40
40
sonchecky
2012-03-30 20:22:19
$6^2 + 2^2 = 36+4 = 040$
$6^2 + 2^2 = 36+4 = 040$
proglote
2012-03-30 20:22:19
040
040
MNL9082
2012-03-30 20:22:19
40
40
copeland
2012-03-30 20:22:23
The minimum value for $|zw|^2$ is $6^2+2^2=\boxed{40}$.
The minimum value for $|zw|^2$ is $6^2+2^2=\boxed{40}$.
copeland
2012-03-30 20:22:28
Notice that we didn't actually solve our original system, but only solved an equation that is implied by our original system. In particular we don't know that there actually is a pair $(z,w)$ such that this system is solved. However we can use $zw=6+2i$ to eliminate $w$ from the first equation and solve for $z$. This shows that we can solve $zw=6+2i$ simultaneously with the first equation.
Notice that we didn't actually solve our original system, but only solved an equation that is implied by our original system. In particular we don't know that there actually is a pair $(z,w)$ such that this system is solved. However we can use $zw=6+2i$ to eliminate $w$ from the first equation and solve for $z$. This shows that we can solve $zw=6+2i$ simultaneously with the first equation.
copeland
2012-03-30 20:22:48
If we can solve the first equation and we can solve the product of the equations, then we can solve the second equation as well (since the right side of both equations is never 0).
If we can solve the first equation and we can solve the product of the equations, then we can solve the second equation as well (since the right side of both equations is never 0).
copeland
2012-03-30 20:23:26
9. Let $x$ and $y$ be real numbers such that $\dfrac{\sin x}{\sin y} = 3$ and $\dfrac{\cos x}{\cos y} = \frac{1}{2}$. The value of $\dfrac{\sin 2x}{\sin 2y} + \dfrac{\cos 2x}{\cos 2y}$ can be expressed in the form $\dfrac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p + q$.
9. Let $x$ and $y$ be real numbers such that $\dfrac{\sin x}{\sin y} = 3$ and $\dfrac{\cos x}{\cos y} = \frac{1}{2}$. The value of $\dfrac{\sin 2x}{\sin 2y} + \dfrac{\cos 2x}{\cos 2y}$ can be expressed in the form $\dfrac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p + q$.
copeland
2012-03-30 20:23:35
Perhaps we can solve this without actually having to compute any of the sines and cosines directly?
Perhaps we can solve this without actually having to compute any of the sines and cosines directly?
copeland
2012-03-30 20:23:39
Can we use trig identities to get at any part of the answer?
Can we use trig identities to get at any part of the answer?
shreyash
2012-03-30 20:24:10
First find sin2x/sin2y
First find sin2x/sin2y
esque
2012-03-30 20:24:10
the first part is immediately 3/2
the first part is immediately 3/2
Imsacred
2012-03-30 20:24:10
sin2x/sin2y
sin2x/sin2y
sonchecky
2012-03-30 20:24:10
sin 2x = 2 sin x cos x
sin 2x = 2 sin x cos x
nmandi7
2012-03-30 20:24:10
sin2x = 2sinxcosx
sin2x = 2sinxcosx
GeorgiaTechMan
2012-03-30 20:24:10
sin(2x)/sin(2y) is easy
sin(2x)/sin(2y) is easy
deepankar
2012-03-30 20:24:10
sin(2x)/sin(2y) = 3/2
sin(2x)/sin(2y) = 3/2
morpheus44
2012-03-30 20:24:10
sin2x/sin2y=sinxcosx/sinycosy=3/2
sin2x/sin2y=sinxcosx/sinycosy=3/2
eccfcco15
2012-03-30 20:24:10
yes, we can get sin(2x)/sin(2y)
yes, we can get sin(2x)/sin(2y)
ABCDE
2012-03-30 20:24:10
multiply them to get sin(2x)/sin(2y)
multiply them to get sin(2x)/sin(2y)
copeland
2012-03-30 20:24:14
The first fraction in the answer is accessible if we use the sine double-angle formula.
The first fraction in the answer is accessible if we use the sine double-angle formula.
copeland
2012-03-30 20:24:19
Specifically, we have\[\frac{\sin 2x}{\sin 2y} = \frac{2 \sin x \cos x}{2 \sin y \cos y}.\]
Specifically, we have\[\frac{\sin 2x}{\sin 2y} = \frac{2 \sin x \cos x}{2 \sin y \cos y}.\]
copeland
2012-03-30 20:24:24
So this term is just\[\frac{\sin x}{\sin y} \cdot \frac{\cos x}{\cos y} = 3 \cdot \frac12 = \frac32.\]
So this term is just\[\frac{\sin x}{\sin y} \cdot \frac{\cos x}{\cos y} = 3 \cdot \frac12 = \frac32.\]
copeland
2012-03-30 20:24:27
Hopefully the other term will be just as easy!
Hopefully the other term will be just as easy!
copeland
2012-03-30 20:24:34
. . . .
. . . .
copeland
2012-03-30 20:24:43
Well, maybe not. The cosine double-angle formula doesn't work as nicely for us.
Well, maybe not. The cosine double-angle formula doesn't work as nicely for us.
copeland
2012-03-30 20:24:49
So I think maybe we sure try to solve for the sines and cosines directly.
So I think maybe we sure try to solve for the sines and cosines directly.
copeland
2012-03-30 20:24:52
Let's set $c = \cos y$ and $s = \sin y$.
Let's set $c = \cos y$ and $s = \sin y$.
copeland
2012-03-30 20:24:57
(I chose these to keep the denominators as simple as possible and to force potentially more complicated stuff in the numerators.)
(I chose these to keep the denominators as simple as possible and to force potentially more complicated stuff in the numerators.)
copeland
2012-03-30 20:25:04
Then what are the trig functions for $x?$
Then what are the trig functions for $x?$
mathswimmer
2012-03-30 20:26:14
sin(x)=3y, cos(x)=c/2
sin(x)=3y, cos(x)=c/2
admin25
2012-03-30 20:26:14
$ \sin x=3s $, $ \cos x=\frac{c}{2} $
$ \sin x=3s $, $ \cos x=\frac{c}{2} $
nackster12
2012-03-30 20:26:14
sin(x)=3s and cos(x)=c/2
sin(x)=3s and cos(x)=c/2
ABCDE
2012-03-30 20:26:14
sinx=3s and 2cosx=c
sinx=3s and 2cosx=c
mathswimmer
2012-03-30 20:26:14
sin(x)=3s, cos(x)=c/2
sin(x)=3s, cos(x)=c/2
lucylai
2012-03-30 20:26:14
3c, s/2
3c, s/2
nmandi7
2012-03-30 20:26:14
sinx=3s
sinx=3s
nmandi7
2012-03-30 20:26:14
cosx=c/2
cosx=c/2
joshxiong
2012-03-30 20:26:14
cos(x)=c/2, sin(x)=3s
cos(x)=c/2, sin(x)=3s
copeland
2012-03-30 20:26:18
$\sin x = 3s$ and $\cos x = \frac12c$.
$\sin x = 3s$ and $\cos x = \frac12c$.
copeland
2012-03-30 20:26:22
But what else do we know?
But what else do we know?
Relativity1618
2012-03-30 20:27:22
set up systems of equations using pythagorean identity
set up systems of equations using pythagorean identity
theone142857
2012-03-30 20:27:22
sum of squares=1
sum of squares=1
brokenfixer
2012-03-30 20:27:22
s^2+c^2=1
s^2+c^2=1
ABCDE
2012-03-30 20:27:22
s^2+c^2=1
s^2+c^2=1
lucylai
2012-03-30 20:27:22
s^2+c^2=1
s^2+c^2=1
admin25
2012-03-30 20:27:22
$ s^2+c^2=1 $, and also $ (3s)^2+(\frac{c}{2})^2=1 $
$ s^2+c^2=1 $, and also $ (3s)^2+(\frac{c}{2})^2=1 $
deepankar
2012-03-30 20:27:22
sin^2(x) + cos^2(x) = 1
sin^2(x) + cos^2(x) = 1
GeorgiaTechMan
2012-03-30 20:27:22
sin(a)^2+cos(a)^2=1 for all a
sin(a)^2+cos(a)^2=1 for all a
sonchecky
2012-03-30 20:27:22
$s^2 + c^2 = 1$ and $(3s)^2 + (c/2)^2 = 1$
$s^2 + c^2 = 1$ and $(3s)^2 + (c/2)^2 = 1$
nmandi7
2012-03-30 20:27:22
9s^2 + c^2/4 = 1
9s^2 + c^2/4 = 1
morpheus44
2012-03-30 20:27:22
9s^2+1/4c^2=1
9s^2+1/4c^2=1
mathswimmer
2012-03-30 20:27:22
s^2+c^2=1, (3s)^2+(c/2)^2=1
s^2+c^2=1, (3s)^2+(c/2)^2=1
joshxiong
2012-03-30 20:27:22
(c/2)^2+9s^2=1 and c^2+s^2=1
(c/2)^2+9s^2=1 and c^2+s^2=1
lucylai
2012-03-30 20:27:22
9s^2+c^2/4=s^2+c^2=1
9s^2+c^2/4=s^2+c^2=1
copeland
2012-03-30 20:27:24
Yep. You lose your licenses for doing trig if you don't try that one first.
Yep. You lose your licenses for doing trig if you don't try that one first.
copeland
2012-03-30 20:27:27
$\sin^2 + \cos^2 = 1!$
$\sin^2 + \cos^2 = 1!$
copeland
2012-03-30 20:27:30
So we have the system of equations
\begin{align*}
s^2 + c^2 &= 1, \\
(3s)^2 + \left(\frac12c\right)^2 &= 1.
\end{align*}
So we have the system of equations
\begin{align*}
s^2 + c^2 &= 1, \\
(3s)^2 + \left(\frac12c\right)^2 &= 1.
\end{align*}
copeland
2012-03-30 20:27:35
We can easily solve this system!
We can easily solve this system!
copeland
2012-03-30 20:27:41
For example, multiply the second equation by 4, then subtract the first from the second, leaving $35s^2 = 3.$
For example, multiply the second equation by 4, then subtract the first from the second, leaving $35s^2 = 3.$
copeland
2012-03-30 20:27:50
This gives the solution\[s^2 = \frac{3}{35},\, c^2 = \frac{32}{35}.\]
This gives the solution\[s^2 = \frac{3}{35},\, c^2 = \frac{32}{35}.\]
copeland
2012-03-30 20:28:03
I'd leave the solution in terms of the squares, because we know that the cosine double-angle formula involves squares.
I'd leave the solution in terms of the squares, because we know that the cosine double-angle formula involves squares.
copeland
2012-03-30 20:28:12
What is the cosine double angle formula?
What is the cosine double angle formula?
ahaanomegas
2012-03-30 20:28:24
There are a few. :P
There are a few. :P
copeland
2012-03-30 20:28:26
Goo!
Goo!
copeland
2012-03-30 20:28:28
er,
er,
copeland
2012-03-30 20:28:29
Good!
Good!
copeland
2012-03-30 20:28:35
Which one is best?
Which one is best?
alex31415
2012-03-30 20:29:08
use cos2x=2cos^2x-1
use cos2x=2cos^2x-1
himym83
2012-03-30 20:29:08
cos 2x = 1-2sin^2x
cos 2x = 1-2sin^2x
ahaanomegas
2012-03-30 20:29:08
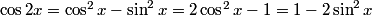
Xcellence
2012-03-30 20:29:08
cos(2u)=1-2sin^2u
cos(2u)=1-2sin^2u
theone142857
2012-03-30 20:29:08
2cos^2-1
2cos^2-1
shreyash
2012-03-30 20:29:08
2cos(x)^2 - 1
2cos(x)^2 - 1
Relativity1618
2012-03-30 20:29:08
1-2sin^2x
1-2sin^2x
theone142857
2012-03-30 20:29:08
2cos^2-1 and 1-2sin^2
2cos^2-1 and 1-2sin^2
copeland
2012-03-30 20:29:20
These are both useful here.
These are both useful here.
copeland
2012-03-30 20:29:25
Indeed,\[\frac{\cos 2x}{\cos 2y} = \frac{2 \cos^2 x - 1}{2 \cos^2 y - 1} = \frac{2(c/2)^2 - 1}{2c^2-1}.\]
Indeed,\[\frac{\cos 2x}{\cos 2y} = \frac{2 \cos^2 x - 1}{2 \cos^2 y - 1} = \frac{2(c/2)^2 - 1}{2c^2-1}.\]
copeland
2012-03-30 20:29:35
I won't torture you with arithmetic.
I won't torture you with arithmetic.
copeland
2012-03-30 20:29:36
We plug in our known $c^2 = \frac{32}{35}$ and we get\[\frac{\frac{16}{35} - 1}{\frac{64}{35} - 1}.\]
We plug in our known $c^2 = \frac{32}{35}$ and we get\[\frac{\frac{16}{35} - 1}{\frac{64}{35} - 1}.\]
copeland
2012-03-30 20:29:42
This simplifies to\[\frac{16 - 35}{64 - 35} = -\frac{19}{29}.\]
This simplifies to\[\frac{16 - 35}{64 - 35} = -\frac{19}{29}.\]
copeland
2012-03-30 20:29:51
And the solution?
And the solution?
matholympiad25
2012-03-30 20:31:20
3/2-19/29=49/58 => 107
3/2-19/29=49/58 => 107
Relativity1618
2012-03-30 20:31:20
49+58=107
49+58=107
brokenfixer
2012-03-30 20:31:20
need 3/2 - 19/29
need 3/2 - 19/29
joshxiong
2012-03-30 20:31:20
3/2-19/29=49/58, so p+q=107
3/2-19/29=49/58, so p+q=107
admin25
2012-03-30 20:31:20
$ \frac{3}{2}-\frac{19}{29}=\frac{49}{58} $
$ \frac{3}{2}-\frac{19}{29}=\frac{49}{58} $
ABCDE
2012-03-30 20:31:20
3/2-19/29=49/58 so 107
3/2-19/29=49/58 so 107
brokenfixer
2012-03-30 20:31:20
(87 - 38) / 58
(87 - 38) / 58
theone142857
2012-03-30 20:31:20
49/58
49/58
googol.plex
2012-03-30 20:31:20
107
107
deepankar
2012-03-30 20:31:26
107
107
Xcellence
2012-03-30 20:31:26
107
107
copeland
2012-03-30 20:31:36
Our final quantity is\[\frac32 - \frac{19}{29} = \frac{87 - 38}{58} = \frac{49}{58},\]these are coprime, so the final answer is $49 + 58 = \boxed{107}$.
Our final quantity is\[\frac32 - \frac{19}{29} = \frac{87 - 38}{58} = \frac{49}{58},\]these are coprime, so the final answer is $49 + 58 = \boxed{107}$.
copeland
2012-03-30 20:32:16
10. Find the number of positive integers $n$ less than 1000 for which there exists a positive real number $x$ such that $n = x \lfloor x \rfloor$.
Note: $\lfloor x \rfloor$ is the greatest integer less than or equal to $x$.
10. Find the number of positive integers $n$ less than 1000 for which there exists a positive real number $x$ such that $n = x \lfloor x \rfloor$.
Note: $\lfloor x \rfloor$ is the greatest integer less than or equal to $x$.
copeland
2012-03-30 20:32:22
What's the first trick to try when dealing with floor?
What's the first trick to try when dealing with floor?
tc1729
2012-03-30 20:33:07
express it with x and fractional part?
express it with x and fractional part?
Hydroxide
2012-03-30 20:33:07
write x=floor(x)+a
write x=floor(x)+a
Voytek
2012-03-30 20:33:07
round down to integers
round down to integers
adamdai97
2012-03-30 20:33:07
write it as x-n
write it as x-n
copeland
2012-03-30 20:33:13
We should write $x=a+r$, where $a$ is an integer and $0\leq r< 1$. The number $a$ is the integer part of $x$ and $r$ is the fractional part.
We should write $x=a+r$, where $a$ is an integer and $0\leq r< 1$. The number $a$ is the integer part of $x$ and $r$ is the fractional part.
copeland
2012-03-30 20:33:18
Now what is $n$ in terms of $a$ and $r$?
Now what is $n$ in terms of $a$ and $r$?
himym83
2012-03-30 20:34:02
n = a(a+r)
n = a(a+r)
lucylai
2012-03-30 20:34:02
a^2+ar
a^2+ar
brokenfixer
2012-03-30 20:34:02
a*(a+r)
a*(a+r)
sonchecky
2012-03-30 20:34:02
$a(a+r)$
$a(a+r)$
nmandi7
2012-03-30 20:34:02
a(a+r)
a(a+r)
19oshawott98
2012-03-30 20:34:02
a^2+ar
a^2+ar
nackster12
2012-03-30 20:34:02
a^2+a*r
a^2+a*r
claudiafeng
2012-03-30 20:34:02
a^2+ar
a^2+ar
Larklight
2012-03-30 20:34:02
a^2+ar
a^2+ar
edisonchew240
2012-03-30 20:34:02
a^{2}+ar
a^{2}+ar
nmandi7
2012-03-30 20:34:02
a^2+ar
a^2+ar
alex31415
2012-03-30 20:34:02
(a+r)a
(a+r)a
copeland
2012-03-30 20:34:07
$n=x\lfloor x\rfloor=(a+r)\lfloor a+r\rfloor=(a+r)a.\]
$n=x\lfloor x\rfloor=(a+r)\lfloor a+r\rfloor=(a+r)a.\]
copeland
2012-03-30 20:34:10
It will help us to have a name for this function, so let $f(x)=x\lfloor x\rfloor$. As above we have
It will help us to have a name for this function, so let $f(x)=x\lfloor x\rfloor$. As above we have
copeland
2012-03-30 20:34:13
$f(a+r)=a(a+r)$ when $a$ is an integer and $0\leq r<1$.
$f(a+r)=a(a+r)$ when $a$ is an integer and $0\leq r<1$.
copeland
2012-03-30 20:34:18
I don't quite see what's going on here yet. What should we do if we don't see what's going on?
I don't quite see what's going on here yet. What should we do if we don't see what's going on?
theone142857
2012-03-30 20:34:55
small cases
small cases
wmcho1007
2012-03-30 20:34:55
put in some numbers as a test
put in some numbers as a test
centralbs
2012-03-30 20:34:55
plug in some values into f(a+r)
plug in some values into f(a+r)
Relativity1618
2012-03-30 20:34:55
plug in values
plug in values
-Transcend-
2012-03-30 20:34:55
Plug in some numbers?
Plug in some numbers?
Seedleaf
2012-03-30 20:34:55
Test a few examples.
Test a few examples.
copeland
2012-03-30 20:34:59
Let's try the smallest examples.
Let's try the smallest examples.
copeland
2012-03-30 20:35:03
Now we are assuming that $x$ is positive, so the smallest that $a$ can be is zero. What $n$ can we get when $a=0$?
Now we are assuming that $x$ is positive, so the smallest that $a$ can be is zero. What $n$ can we get when $a=0$?
shreyash
2012-03-30 20:35:43
0
0
nackster12
2012-03-30 20:35:43
0
0
coldsummer
2012-03-30 20:35:43
0
0
19oshawott98
2012-03-30 20:35:43
0
0
nmandi7
2012-03-30 20:35:43
0
0
wmcho1007
2012-03-30 20:35:43
then its 0
then its 0
n2010Math
2012-03-30 20:35:43
0
0
copeland
2012-03-30 20:35:47
When $a=0$, we always get $0(0+x)=0$. This is not a positive integer so we can ignore this case.
When $a=0$, we always get $0(0+x)=0$. This is not a positive integer so we can ignore this case.
copeland
2012-03-30 20:35:50
What do we get if $a=1$?
What do we get if $a=1$?
copeland
2012-03-30 20:36:28
What do we get for $f$, that is?
What do we get for $f$, that is?
Duncanyang
2012-03-30 20:36:31
f(1+r)=1+r
f(1+r)=1+r
shreyash
2012-03-30 20:36:31
1+r
1+r
Relativity1618
2012-03-30 20:36:31
1+r
1+r
centralbs
2012-03-30 20:36:31
1+r
1+r
copeland
2012-03-30 20:36:46
When $a=1$, we get $f(1+r)=1(1+r)=1+r$. Since $0\leq r<1$, we get $1\leq f(a+r)<2$, so the possible outputs of $f$ are exactly the numbers in the interval $[1,2)$.
When $a=1$, we get $f(1+r)=1(1+r)=1+r$. Since $0\leq r<1$, we get $1\leq f(a+r)<2$, so the possible outputs of $f$ are exactly the numbers in the interval $[1,2)$.
copeland
2012-03-30 20:36:54
How many integers are in this interval?
How many integers are in this interval?
zinko1991
2012-03-30 20:37:20
n=1
n=1
ytao
2012-03-30 20:37:20
1
1
flyrain
2012-03-30 20:37:20
1
1
himym83
2012-03-30 20:37:20
1
1
Imsacred
2012-03-30 20:37:20
1; 1
1; 1
admin25
2012-03-30 20:37:20
Just one.
Just one.
Xcellence
2012-03-30 20:37:20
one
one
joshxiong
2012-03-30 20:37:20
1, that is 1.
1, that is 1.
sinnoel
2012-03-30 20:37:20
`1
`1
deepankar
2012-03-30 20:37:20
1
1
copeland
2012-03-30 20:37:27
Just $n=1$.
Just $n=1$.
copeland
2012-03-30 20:37:30
What do we get when $a=2$?
What do we get when $a=2$?
theone142857
2012-03-30 20:37:53
4+2r
4+2r
Relativity1618
2012-03-30 20:37:53
4+2r
4+2r
ptes77
2012-03-30 20:37:53
4+2r
4+2r
Hydroxide
2012-03-30 20:37:53
2(2+r)=4+2r
2(2+r)=4+2r
Duncanyang
2012-03-30 20:37:53
2(2+r)
2(2+r)
nackster12
2012-03-30 20:37:53
4+2r
4+2r
alex31415
2012-03-30 20:37:53
2(2+r)=4+2r
2(2+r)=4+2r
copeland
2012-03-30 20:38:07
When $a=2$, we get $f(2+r)=2(2+r)=2+2r$. Since $0\leq 2r<2$, we get $4\leq f(a+r)<6$, so the possible outputs of $f$ are exactly the numbers in the interval $[4,6)$.
When $a=2$, we get $f(2+r)=2(2+r)=2+2r$. Since $0\leq 2r<2$, we get $4\leq f(a+r)<6$, so the possible outputs of $f$ are exactly the numbers in the interval $[4,6)$.
copeland
2012-03-30 20:38:11
How many integers are in this interval?
How many integers are in this interval?
googol.plex
2012-03-30 20:38:42
2
2
mathswimmer
2012-03-30 20:38:42
2
2
sonchecky
2012-03-30 20:38:42
2 (namely 4 and 5)
2 (namely 4 and 5)
CantonMathGuy
2012-03-30 20:38:42
2
2
mathnerd101
2012-03-30 20:38:42
2
2
joshxiong
2012-03-30 20:38:42
4,5, so 2.
4,5, so 2.
Imsacred
2012-03-30 20:38:42
2; 4 and 5
2; 4 and 5
copeland
2012-03-30 20:38:47
Two: 4 and 5.
Two: 4 and 5.
copeland
2012-03-30 20:38:50
What do we get when $a=3$?
What do we get when $a=3$?
theone142857
2012-03-30 20:39:20
9+3r
9+3r
-Transcend-
2012-03-30 20:39:20
9+3r
9+3r
Duncanyang
2012-03-30 20:39:20
3(3+r)
3(3+r)
shreyash
2012-03-30 20:39:20
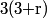
Relativity1618
2012-03-30 20:39:20
9+3r
9+3r
flyrain
2012-03-30 20:39:20
f(3+r)= 9+3r
f(3+r)= 9+3r
Hydroxide
2012-03-30 20:39:20
3(3+r)=9+3r
3(3+r)=9+3r
nackster12
2012-03-30 20:39:20
9+3r
9+3r
copeland
2012-03-30 20:39:24
When $a=3$, we get $f(3+r)=3(3+r)=3+3r$. Since $0\leq 3r<3$, we get $9\leq f(a+r)<12$, so the possible outputs of $f$ are exactly the numbers in the interval $[9,12)$.
When $a=3$, we get $f(3+r)=3(3+r)=3+3r$. Since $0\leq 3r<3$, we get $9\leq f(a+r)<12$, so the possible outputs of $f$ are exactly the numbers in the interval $[9,12)$.
copeland
2012-03-30 20:39:27
How many integers are in this interval?
How many integers are in this interval?
lucylai
2012-03-30 20:40:02
3
3
n2010Math
2012-03-30 20:40:02
[9,12), so 3 - 9,10,11
[9,12), so 3 - 9,10,11
sonchecky
2012-03-30 20:40:02
3 (9, 10, and 11)
3 (9, 10, and 11)
nackster12
2012-03-30 20:40:02
3
3
shreyash
2012-03-30 20:40:02
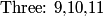
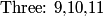
adamdai97
2012-03-30 20:40:02
3-9,10,11
3-9,10,11
-Transcend-
2012-03-30 20:40:02
3
3
nmandi7
2012-03-30 20:40:02
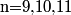
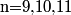
wmcho1007
2012-03-30 20:40:02
9,10,11, so 3
9,10,11, so 3
Duncanyang
2012-03-30 20:40:02
3
3
copeland
2012-03-30 20:40:06
Three: 9, 10, and 11.
Three: 9, 10, and 11.
copeland
2012-03-30 20:40:09
And for an arbitrary $a$, what do we get?
And for an arbitrary $a$, what do we get?
sinnoel
2012-03-30 20:40:38
a
a
Duncanyang
2012-03-30 20:40:38
a(a+r)
a(a+r)
nmandi7
2012-03-30 20:40:38


googol.plex
2012-03-30 20:40:38
it should be a
it should be a
Xcellence
2012-03-30 20:40:38
a integers
a integers
Duncanyang
2012-03-30 20:40:38
and a integers possible
and a integers possible
adamdai97
2012-03-30 20:40:38
there are a numbers that work
there are a numbers that work
sonchecky
2012-03-30 20:40:38
a integers (a^2, a^2 + 1, ... a(a-1) - 1)
a integers (a^2, a^2 + 1, ... a(a-1) - 1)
awesomemathlete
2012-03-30 20:40:38
a
a
copeland
2012-03-30 20:40:57
For arbitrary (integers) $a$ we get we get $f(a+r)=a(a+r)=a+ar$. Since $0\leq ar<a$, we get $a^2\leq f(a+r)<a^2+a$, so the possible outputs of $f$ are exactly the numbers in the interval $[a^2,a^2+a)$.
For arbitrary (integers) $a$ we get we get $f(a+r)=a(a+r)=a+ar$. Since $0\leq ar<a$, we get $a^2\leq f(a+r)<a^2+a$, so the possible outputs of $f$ are exactly the numbers in the interval $[a^2,a^2+a)$.
copeland
2012-03-30 20:41:01
The integers in this interval are $\{a^2,a^2+1,\ldots,a^2+a-1\}$. There are $a$ integers in this interval.
The integers in this interval are $\{a^2,a^2+1,\ldots,a^2+a-1\}$. There are $a$ integers in this interval.
copeland
2012-03-30 20:41:10
Can we just add these up and be done?
Can we just add these up and be done?
copeland
2012-03-30 20:41:49
Two things:
Two things:
alex31415
2012-03-30 20:41:52
floor(sqrt1000)=31
floor(sqrt1000)=31
sonchecky
2012-03-30 20:41:52
We need the upper limit for a
We need the upper limit for a
theone142857
2012-03-30 20:41:52
less than 1000
less than 1000
nmandi7
2012-03-30 20:41:52
must be <1000
must be <1000
nackster12
2012-03-30 20:41:52
we need to check where we add up to
we need to check where we add up to
Imsacred
2012-03-30 20:41:52
well we have to check to make sure all of the numbers are under 1000
well we have to check to make sure all of the numbers are under 1000
copeland
2012-03-30 20:41:56
We'll get to that.
We'll get to that.
centralbs
2012-03-30 20:42:01
We must ensure that there is no overlap in the intervals
We must ensure that there is no overlap in the intervals
heliootrope
2012-03-30 20:42:01
check for double-counted integers?
check for double-counted integers?
copeland
2012-03-30 20:42:10
This is scarier for me, though.
This is scarier for me, though.
copeland
2012-03-30 20:42:14
We need to check that all of the intervals are disjoint.
We need to check that all of the intervals are disjoint.
copeland
2012-03-30 20:42:16
Are they?
Are they?
brokenfixer
2012-03-30 20:42:54
a^2 + a - 1 < (a+1)^2 yep
a^2 + a - 1 < (a+1)^2 yep
himym83
2012-03-30 20:42:54
yes: a^2+a < a^2+2a+1
yes: a^2+a < a^2+2a+1
sonchecky
2012-03-30 20:42:54
Yes because $(a+1)^2 = a^2 + 2a + 1 > a^2 + a$
Yes because $(a+1)^2 = a^2 + 2a + 1 > a^2 + a$
theone142857
2012-03-30 20:42:54
But that's obvious due to the fact that a^2-a+1<(a+1)^2
But that's obvious due to the fact that a^2-a+1<(a+1)^2
nackster12
2012-03-30 20:42:54
yes since (a)(a+1) is less than (a+1)(a+1)
yes since (a)(a+1) is less than (a+1)(a+1)
admin25
2012-03-30 20:42:54
Yes: $ a^2+a-1<(a+1)^2 $
Yes: $ a^2+a-1<(a+1)^2 $
copeland
2012-03-30 20:43:00
$a(a+1)$ is the rightmost endpoint of the $a^{th}$ interval and $(a+1)(a+1)$ is the leftmost endpoint of the next interval, so these intervals are disjoint.
$a(a+1)$ is the rightmost endpoint of the $a^{th}$ interval and $(a+1)(a+1)$ is the leftmost endpoint of the next interval, so these intervals are disjoint.
copeland
2012-03-30 20:43:05
The first interval is $[1,2)$. What is the last interval?
The first interval is $[1,2)$. What is the last interval?
alex31415
2012-03-30 20:43:53
[961,992)
[961,992)
himym83
2012-03-30 20:43:53
[961,992)
[961,992)
Imsacred
2012-03-30 20:43:53
[961,992)
[961,992)
shreyash
2012-03-30 20:43:53
[961,992)
[961,992)
sonchecky
2012-03-30 20:43:53
[961, 992)
[961, 992)
19oshawott98
2012-03-30 20:43:53
961-991
961-991
brokenfixer
2012-03-30 20:43:53
31^2 to 31^2+31-1
31^2 to 31^2+31-1
copeland
2012-03-30 20:44:01
Since $31^2=961$ and $32^2=1024$, the last interval we need to deal with is $[31^2,31\cdot32)$.
Since $31^2=961$ and $32^2=1024$, the last interval we need to deal with is $[31^2,31\cdot32)$.
copeland
2012-03-30 20:44:14
Here was something that should have made us nervous:
Here was something that should have made us nervous:
googol.plex
2012-03-30 20:44:18
There might be a partial thing at the end
There might be a partial thing at the end
copeland
2012-03-30 20:44:36
Fortuitously, all 31 of the numbers are less than 1000 so the counting is much easier.
Fortuitously, all 31 of the numbers are less than 1000 so the counting is much easier.
copeland
2012-03-30 20:44:40
So what is the answer?
So what is the answer?
Relativity1618
2012-03-30 20:45:18
so 31*32/2=496
so 31*32/2=496
Relativity1618
2012-03-30 20:45:18
496
496
alex31415
2012-03-30 20:45:18
496
496
GeorgiaTechMan
2012-03-30 20:45:18
496
496
Duncanyang
2012-03-30 20:45:18
496
496
shreyash
2012-03-30 20:45:18
496
496
theone142857
2012-03-30 20:45:18
496
496
proglote
2012-03-30 20:45:18
31*32/2 = 496
31*32/2 = 496
himym83
2012-03-30 20:45:18
1+2+3+...+31 = (31)(32)/2 = 496
1+2+3+...+31 = (31)(32)/2 = 496
-Transcend-
2012-03-30 20:45:18
496
496
eccfcco15
2012-03-30 20:45:18
496
496
wmcho1007
2012-03-30 20:45:18
1+2+3+4+....+30+31=496
1+2+3+4+....+30+31=496
vjnmath
2012-03-30 20:45:18
31*16 = 496
31*16 = 496
numbertheorist17
2012-03-30 20:45:18
496
496
GeorgiaTechMan
2012-03-30 20:45:21
yay perfect numbers
yay perfect numbers
Relativity1618
2012-03-30 20:45:21
3rd perfect number
3rd perfect number
copeland
2012-03-30 20:45:26
Since the intervals are disjoint we need to add the number of elements in all of them:\[1+2+3+\cdots+31=\frac{31\cdot32}2=\boxed{496}.\]
Since the intervals are disjoint we need to add the number of elements in all of them:\[1+2+3+\cdots+31=\frac{31\cdot32}2=\boxed{496}.\]
copeland
2012-03-30 20:45:34
Phew. 10 down.
Phew. 10 down.
copeland
2012-03-30 20:45:37
Man we're good.
Man we're good.
danielguo94
2012-03-30 20:46:02
Yay.
Yay.
-Transcend-
2012-03-30 20:46:02
yay!
yay!
Duncanyang
2012-03-30 20:46:02
yay.
yay.
copeland
2012-03-30 20:46:06
11. Let $f_1(x) = \frac{2}{3} - \frac{3}{3x + 1}$, and for $n \ge 1$, define $f_n(x) = f_1 (f_{n - 1}(x))$. The value of $x$ that satisfies $f_{1001}(x) = x - 3$ can be expressed in the form $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m + n$.
11. Let $f_1(x) = \frac{2}{3} - \frac{3}{3x + 1}$, and for $n \ge 1$, define $f_n(x) = f_1 (f_{n - 1}(x))$. The value of $x$ that satisfies $f_{1001}(x) = x - 3$ can be expressed in the form $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m + n$.
copeland
2012-03-30 20:46:15
Does anybody know the name of this type of function?
Does anybody know the name of this type of function?
brokenfixer
2012-03-30 20:46:47
moebius transformations
moebius transformations
copeland
2012-03-30 20:46:52
This type of of function is a called a Mobius transformation.
This type of of function is a called a Mobius transformation.
copeland
2012-03-30 20:46:56
(There should be dots: Möbius, but they're annoying to type.)
(There should be dots: Möbius, but they're annoying to type.)
copeland
2012-03-30 20:47:00
A Mobius transformation has the form $g(x)=\frac{ax+b}{cx+d}$. Ours is in disguise though:
A Mobius transformation has the form $g(x)=\frac{ax+b}{cx+d}$. Ours is in disguise though:
copeland
2012-03-30 20:47:06
\[f_1(x)=\frac23-\frac{3}{3x+1}=\frac{6x+2}{9x+3}-\frac{9}{9x+3}=\frac{6x-7}{9x+3}.\]
\[f_1(x)=\frac23-\frac{3}{3x+1}=\frac{6x+2}{9x+3}-\frac{9}{9x+3}=\frac{6x-7}{9x+3}.\]
copeland
2012-03-30 20:47:12
(Henceforth I'm going to use $f$ to denote $f_1$, since that's easier.)
(Henceforth I'm going to use $f$ to denote $f_1$, since that's easier.)
copeland
2012-03-30 20:47:16
When you see a Mobius transformation on a math contest, what's the first thing you should assume?
When you see a Mobius transformation on a math contest, what's the first thing you should assume?
danielguo94
2012-03-30 20:48:07
cyclicity
cyclicity
himym83
2012-03-30 20:48:07
function is cyclic
function is cyclic
ABCDE
2012-03-30 20:48:07
it repeats?
it repeats?
Imsacred
2012-03-30 20:48:07
it cycles?
it cycles?
sonchecky
2012-03-30 20:48:07
$f_n(x) = x$ for some n
$f_n(x) = x$ for some n
CantonMathGuy
2012-03-30 20:48:07
it repeats
it repeats
wmcho1007
2012-03-30 20:48:07
it's going to repeat after some time
it's going to repeat after some time
lucylai
2012-03-30 20:48:07
it's cyclic
it's cyclic
copeland
2012-03-30 20:48:11
It's probably periodic (meaning applying it the right number of times gives back the identity). Most math contest Mobius transformations are periodic. There's a really good hint to this in the problem, too: we want to iterate the function 1001 times.
It's probably periodic (meaning applying it the right number of times gives back the identity). Most math contest Mobius transformations are periodic. There's a really good hint to this in the problem, too: we want to iterate the function 1001 times.
copeland
2012-03-30 20:48:21
Don't get the wrong idea here. Mobius transformations are very interesting and useful in mathematics. If you pull one out of the blue, it almost certainly will not be periodic. If you meet one at your next swim meet, it's probably not periodic. If you run across one on a math contest, however, it is likely that it will turn out to be periodic.
Don't get the wrong idea here. Mobius transformations are very interesting and useful in mathematics. If you pull one out of the blue, it almost certainly will not be periodic. If you meet one at your next swim meet, it's probably not periodic. If you run across one on a math contest, however, it is likely that it will turn out to be periodic.
copeland
2012-03-30 20:48:32
So our goal now should be to find the period.
So our goal now should be to find the period.
copeland
2012-03-30 20:48:45
We could iterate our function, but that sounds tedious. is there a nice number we should start with instead?
We could iterate our function, but that sounds tedious. is there a nice number we should start with instead?
centralbs
2012-03-30 20:49:24
0
0
theone142857
2012-03-30 20:49:24
x=0
x=0
Relativity1618
2012-03-30 20:49:24
0
0
zinko1991
2012-03-30 20:49:24
0
0
theone142857
2012-03-30 20:49:24
x=7/6
x=7/6
brokenfixer
2012-03-30 20:49:24
x = 0
x = 0
copeland
2012-03-30 20:49:28
There are actually two nice choices:
There are actually two nice choices:
copeland
2012-03-30 20:49:32
We can apply the function to $x=0$ to get \[f(0)=\frac{-7}3.\]
We can apply the function to $x=0$ to get \[f(0)=\frac{-7}3.\]
copeland
2012-03-30 20:49:36
We could also apply the function to $x=\frac76$ to get \[\frac{6\cdot\frac76-7}{\text{stuff}}=\frac{7-7}{\text{stuff}}=0.\]
We could also apply the function to $x=\frac76$ to get \[\frac{6\cdot\frac76-7}{\text{stuff}}=\frac{7-7}{\text{stuff}}=0.\]
copeland
2012-03-30 20:49:59
Yeah, I'm down with stuff, too. Stuff rules.
Yeah, I'm down with stuff, too. Stuff rules.
zinko1991
2012-03-30 20:50:04
i like stuff
i like stuff
copeland
2012-03-30 20:50:10
You know what else rules? Things rule.
You know what else rules? Things rule.
copeland
2012-03-30 20:50:13
What is $f\left(-\tfrac73\right)$?
What is $f\left(-\tfrac73\right)$?
lucylai
2012-03-30 20:51:17
7/6 wow
7/6 wow
alex31415
2012-03-30 20:51:17
7/6
7/6
matholympiad25
2012-03-30 20:51:17
7/6
7/6
ABCDE
2012-03-30 20:51:17
7/6
7/6
admin25
2012-03-30 20:51:17
Woah, $ \frac{7}{6} $
Woah, $ \frac{7}{6} $
nackster12
2012-03-30 20:51:17
7/6
7/6
googol.plex
2012-03-30 20:51:17
7/6
7/6
ptes77
2012-03-30 20:51:17
7/6
7/6
Duncanyang
2012-03-30 20:51:17
2/3+1/2=7/6
2/3+1/2=7/6
Relativity1618
2012-03-30 20:51:17
$\frac{7}{6}$
$\frac{7}{6}$
Yongyi781
2012-03-30 20:51:17
7/6
7/6
copeland
2012-03-30 20:51:19
$f\left(-\tfrac73\right)=\frac{6\left(-\tfrac73\right)-7}{9\left(-\tfrac73\right)+3}=\frac{6(-7)-7\cdot3}{9(-7)+3\cdot3}=\frac{9(-7)}{9(-6)}=\frac76$
$f\left(-\tfrac73\right)=\frac{6\left(-\tfrac73\right)-7}{9\left(-\tfrac73\right)+3}=\frac{6(-7)-7\cdot3}{9(-7)+3\cdot3}=\frac{9(-7)}{9(-6)}=\frac76$
copeland
2012-03-30 20:51:32
And what is $f\left(\tfrac76\right)$?
And what is $f\left(\tfrac76\right)$?
Relativity1618
2012-03-30 20:51:56
and f(7/6)=0
and f(7/6)=0
Relativity1618
2012-03-30 20:51:56
so the period is 3
so the period is 3
numbertheorist17
2012-03-30 20:51:56
0
0
numbertheorist17
2012-03-30 20:51:56
0
0
nmandi7
2012-03-30 20:51:56
0
0
nackster12
2012-03-30 20:51:56
0
0
himym83
2012-03-30 20:51:56
zero
zero
theone142857
2012-03-30 20:51:56
0
0
ABCDE
2012-03-30 20:51:56
0!
0!
Xcellence
2012-03-30 20:51:56
0
0
adamdai97
2012-03-30 20:51:56
0
0
flyrain
2012-03-30 20:51:56
0!
0!
kmc927
2012-03-30 20:51:56
0
0
shreyash
2012-03-30 20:51:56
0
0
loserboy
2012-03-30 20:51:56
0
0
19oshawott98
2012-03-30 20:51:56
0
0
admin25
2012-03-30 20:51:56
$ 0 $! It's repeating! :D
$ 0 $! It's repeating! :D
copeland
2012-03-30 20:52:00
We already know that this gives 0.
We already know that this gives 0.
copeland
2012-03-30 20:52:04
This does not prove that $f$ has period 3. This proves only that if $f$ is periodic at all, then the period is a multiple of 3. That's OK. For now let's work on the assumption that $f$ does have period 3. Therefore $f(f(f(x)))=x$ for every $x$.
This does not prove that $f$ has period 3. This proves only that if $f$ is periodic at all, then the period is a multiple of 3. That's OK. For now let's work on the assumption that $f$ does have period 3. Therefore $f(f(f(x)))=x$ for every $x$.
copeland
2012-03-30 20:52:28
(Incidentally, I conjectured the period was 6 when I first looked at this problem.)
(Incidentally, I conjectured the period was 6 when I first looked at this problem.)
copeland
2012-03-30 20:52:36
Periodicity means that $f_{n+3}=f_n$. In particular we are conjecturing that $f_{1001}=f_2$.
Periodicity means that $f_{n+3}=f_n$. In particular we are conjecturing that $f_{1001}=f_2$.
copeland
2012-03-30 20:52:48
So next we ought to try to solve the equation $f_2(x)=x-3$.
So next we ought to try to solve the equation $f_2(x)=x-3$.
copeland
2012-03-30 20:52:53
Darn! This means we have to apply $f$ twice, right?
Darn! This means we have to apply $f$ twice, right?
brokenfixer
2012-03-30 20:53:43
take f(x-3)
take f(x-3)
Duncanyang
2012-03-30 20:53:43
iterate this.
iterate this.
copeland
2012-03-30 20:53:46
If $f$ is periodic, then we can apply $f$ to this equation to get $f_3(x)=f(x-3)$ so $f(x-3)=x$. That should be easier to solve.
If $f$ is periodic, then we can apply $f$ to this equation to get $f_3(x)=f(x-3)$ so $f(x-3)=x$. That should be easier to solve.
copeland
2012-03-30 20:53:58
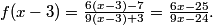
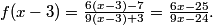
copeland
2012-03-30 20:54:01
We want this to be equal to $x$, so we want to solve \[x=\frac{6x-25}{9x-24}.\]
We want this to be equal to $x$, so we want to solve \[x=\frac{6x-25}{9x-24}.\]
copeland
2012-03-30 20:54:08
Cross-multiplying gives \[9x^2-24x=6x-25\]or\[9x^2-30x+25=0.\]
Cross-multiplying gives \[9x^2-24x=6x-25\]or\[9x^2-30x+25=0.\]
copeland
2012-03-30 20:54:13
What are the solutions to this quadratic?
What are the solutions to this quadratic?
alex31415
2012-03-30 20:54:42
x=5/3 is the only solution
x=5/3 is the only solution
Duncanyang
2012-03-30 20:54:42
x=5/3 only
x=5/3 only
success
2012-03-30 20:54:42
5/3
5/3
sonchecky
2012-03-30 20:54:42
(3x-5)^2 = 0, so x = 5/3
(3x-5)^2 = 0, so x = 5/3
ytao
2012-03-30 20:54:42
5/3 with multiplicity 2.
5/3 with multiplicity 2.
kmc927
2012-03-30 20:54:42
5/3
5/3
herro66
2012-03-30 20:54:42
5/3
5/3
lucylai
2012-03-30 20:54:42
double root, 5/3
double root, 5/3
nackster12
2012-03-30 20:54:42
5/3
5/3
19oshawott98
2012-03-30 20:54:42
5/3
5/3
admin25
2012-03-30 20:54:42
It's a perfect square! So $ x=\frac{5}{3} $
It's a perfect square! So $ x=\frac{5}{3} $
theGCF
2012-03-30 20:54:42
5/3
5/3
herro66
2012-03-30 20:54:42
5/3
5/3
joshxiong
2012-03-30 20:54:42
(3x-5)^2=0, so 5/3
(3x-5)^2=0, so 5/3
coldsummer
2012-03-30 20:54:42
it has solution 5/3
it has solution 5/3
copeland
2012-03-30 20:54:46
The quadratic is a square! \[9x^2-30x+25=(3x-5)^2.\] The only solution is $\frac53$.
The quadratic is a square! \[9x^2-30x+25=(3x-5)^2.\] The only solution is $\frac53$.
copeland
2012-03-30 20:54:49
Remember, though, that we assumed $f$ was periodic. We actually don't need anything that strong to show that $f_{1001}(\frac53)=\frac53-3.$ We can look just as what successively applications of $f$ do to the value $\frac53$.
Remember, though, that we assumed $f$ was periodic. We actually don't need anything that strong to show that $f_{1001}(\frac53)=\frac53-3.$ We can look just as what successively applications of $f$ do to the value $\frac53$.
copeland
2012-03-30 20:55:03
Notice $f_1\left(\frac53\right)=\frac23-\frac3{3\cdot\frac53+1}=\frac23-\frac12=\frac16$.
Notice $f_1\left(\frac53\right)=\frac23-\frac3{3\cdot\frac53+1}=\frac23-\frac12=\frac16$.
copeland
2012-03-30 20:55:22
Then $f_2\left(\frac53\right)=f\left(\frac16\right)=\frac23-\frac3{3\cdot\frac16+1}\frac23-2=-\frac43$.
Then $f_2\left(\frac53\right)=f\left(\frac16\right)=\frac23-\frac3{3\cdot\frac16+1}\frac23-2=-\frac43$.
copeland
2012-03-30 20:55:32
Finally we note that $-\frac43=\frac53-3$ and $f\left(\frac53-3\right)=\frac53$, so these three values do repeat, and $f_{1001}\left(\frac53\right)=-\frac43=\frac53-3$.
Finally we note that $-\frac43=\frac53-3$ and $f\left(\frac53-3\right)=\frac53$, so these three values do repeat, and $f_{1001}\left(\frac53\right)=-\frac43=\frac53-3$.
copeland
2012-03-30 20:55:42
So. . . .
So. . . .
shreyash
2012-03-30 20:56:37
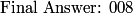
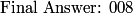
theone142857
2012-03-30 20:56:37
008
008
alex31415
2012-03-30 20:56:37
zinko1991
2012-03-30 20:56:37
answer it 8
answer it 8
-Transcend-
2012-03-30 20:56:37
008
008
GeorgiaTechMan
2012-03-30 20:56:37
our answer is 5+3=8!
our answer is 5+3=8!
mathswimmer
2012-03-30 20:56:37
008
008
googol.plex
2012-03-30 20:56:37
the answer is $\boxed {8}$
the answer is $\boxed {8}$
copeland
2012-03-30 20:56:40
The answer to the problem is $5+3=\boxed{008}$.
The answer to the problem is $5+3=\boxed{008}$.
copeland
2012-03-30 20:57:19
12. For a positive integer $p$, define the positive integer $n$ to be $p$-safe if $n$ differs in absolute value by more than 2 from all multiples of $p$. For example, the set of 10-safe numbers is $\{3, 4, 5, 6, 7, 13, 14, 15, 16, 17, 23, \dots\}$. Find the number of positive integers less than or equal to 10,000 which are simultaneously 7-safe, 11-safe, and 13-safe.
12. For a positive integer $p$, define the positive integer $n$ to be $p$-safe if $n$ differs in absolute value by more than 2 from all multiples of $p$. For example, the set of 10-safe numbers is $\{3, 4, 5, 6, 7, 13, 14, 15, 16, 17, 23, \dots\}$. Find the number of positive integers less than or equal to 10,000 which are simultaneously 7-safe, 11-safe, and 13-safe.
copeland
2012-03-30 20:57:28
How can we tell if a number is 7-safe?
How can we tell if a number is 7-safe?
Relativity1618
2012-03-30 20:58:03
3 or 4 mod 7
3 or 4 mod 7
GeorgiaTechMan
2012-03-30 20:58:03
congruent to 3 or 4 mod 7
congruent to 3 or 4 mod 7
alex31415
2012-03-30 20:58:03
if it is 3 or 4 mod 7
if it is 3 or 4 mod 7
numberdance
2012-03-30 20:58:03
3 or 4 mod 7
3 or 4 mod 7
googol.plex
2012-03-30 20:58:03
It's 3 or 4 mod 7
It's 3 or 4 mod 7
awesomemathlete
2012-03-30 20:58:03
3 or 4 mod 7
3 or 4 mod 7
nackster12
2012-03-30 20:58:03
the number is congruent to 3 or 4 mod 7
the number is congruent to 3 or 4 mod 7
ABCDE
2012-03-30 20:58:03
n==3 or 4 (mod 7)
n==3 or 4 (mod 7)
Imsacred
2012-03-30 20:58:03
n is 7-safe if n-3 or n-4 is a multiple of 7
n is 7-safe if n-3 or n-4 is a multiple of 7
copeland
2012-03-30 20:58:06
The 7-safe numbers are the ones that are congruent to 3 or 4 mod 7.
The 7-safe numbers are the ones that are congruent to 3 or 4 mod 7.
copeland
2012-03-30 20:58:09
How can we tell if a number is 11-safe?
How can we tell if a number is 11-safe?
alex31415
2012-03-30 20:58:44
3-8 mod 11
3-8 mod 11
himym83
2012-03-30 20:58:44
3,4,5,6,7,8 mod 7
3,4,5,6,7,8 mod 7
hodgeheg
2012-03-30 20:58:44
if it is congruent to 3, 4, 5, 6, 7, 8, mod 11
if it is congruent to 3, 4, 5, 6, 7, 8, mod 11
ahaanomegas
2012-03-30 20:58:44
It is 3, 4, 5, 6, 7, or 8 (mod 11).
It is 3, 4, 5, 6, 7, or 8 (mod 11).
googol.plex
2012-03-30 20:58:44
3, 4, 5, 6, 7, 8 mod 11
3, 4, 5, 6, 7, 8 mod 11
-Transcend-
2012-03-30 20:58:44
3, 4, 5, 6, 7, 8 mod 11
3, 4, 5, 6, 7, 8 mod 11
19oshawott98
2012-03-30 20:58:44
3,4,5,6,7,8mod11
3,4,5,6,7,8mod11
copeland
2012-03-30 20:58:48
The 11-safe numbers are the ones that are congruent to 3, 4, 5, 6, 7, or 8 mod 11.
The 11-safe numbers are the ones that are congruent to 3, 4, 5, 6, 7, or 8 mod 11.
copeland
2012-03-30 20:58:51
How can we tell if a number is 13-safe?
How can we tell if a number is 13-safe?
awesomemathlete
2012-03-30 20:59:40
3-10 mod 13
3-10 mod 13
ptes77
2012-03-30 20:59:40
3-10 mod 13
3-10 mod 13
sonchecky
2012-03-30 20:59:40
congruent to 3-10 mod 13
congruent to 3-10 mod 13
Mary_Posa
2012-03-30 20:59:40
3-10 mod 13
3-10 mod 13
-Transcend-
2012-03-30 20:59:40
3 to 10 mod 13
3 to 10 mod 13
brokenfixer
2012-03-30 20:59:40
same: congruent to 3,4,5,6,7,8,9,10 mod 13
same: congruent to 3,4,5,6,7,8,9,10 mod 13
adamdai97
2012-03-30 20:59:40
3,4,5,6,7,8,9,10 mod 13
3,4,5,6,7,8,9,10 mod 13
ahaanomegas
2012-03-30 20:59:40
It is 3, 4, 5, 6, 7, 8, 9, or 10 (mod 13).
It is 3, 4, 5, 6, 7, 8, 9, or 10 (mod 13).
numberdance
2012-03-30 20:59:40
Congruent to 3, 4, 5, 6, 7, 8, 9, or 10 mod 13
Congruent to 3, 4, 5, 6, 7, 8, 9, or 10 mod 13
Xcellence
2012-03-30 20:59:40
must be congruent to 3,4,5,6,7,8,9,10 mod 13
must be congruent to 3,4,5,6,7,8,9,10 mod 13
wmcho1007
2012-03-30 20:59:40
3,4,5,6,7,8,9,10 mod 13
3,4,5,6,7,8,9,10 mod 13
copeland
2012-03-30 20:59:45
The 13-safe numbers are the ones that are congruent to 3, 4, 5, 6, 7, 8, 9, and 10 mod 13.
The 13-safe numbers are the ones that are congruent to 3, 4, 5, 6, 7, 8, 9, and 10 mod 13.
copeland
2012-03-30 20:59:52
What theorem do we want to apply here?
What theorem do we want to apply here?
Relativity1618
2012-03-30 21:00:35
chinese remainder theorem
chinese remainder theorem
GeorgiaTechMan
2012-03-30 21:00:35
Chinese remainder theorem kills this problem
Chinese remainder theorem kills this problem
19oshawott98
2012-03-30 21:00:35
we can use the CRT?
we can use the CRT?
Relativity1618
2012-03-30 21:00:35
chinese remainder theorem
chinese remainder theorem
brokenfixer
2012-03-30 21:00:35
chinese remainder
chinese remainder
mcdonalds106_7
2012-03-30 21:00:35
CRT
CRT
himym83
2012-03-30 21:00:35
chinese remainder theorem?
chinese remainder theorem?
alex31415
2012-03-30 21:00:35
CHinese remainder theorem?
CHinese remainder theorem?
19oshawott98
2012-03-30 21:00:35
Chinese remainder theorem
Chinese remainder theorem
nackster12
2012-03-30 21:00:35
chinese remainder theorem
chinese remainder theorem
MNL9082
2012-03-30 21:00:35
chinese remainder theorem
chinese remainder theorem
theone142857
2012-03-30 21:00:35
Chinese remainder thereom
Chinese remainder thereom
danielguo94
2012-03-30 21:00:35
chinese remainder
chinese remainder
copeland
2012-03-30 21:00:45
The Chinese Remainder Theorem tells us that for every $x$, $y$, and $z$, there is exactly one residue class modulo $7\cdot11\cdot13=1001$ such that the numbers $N$ in this residue class simultaneously solve
\begin{align*}
N\equiv x\pmod 7\\
N\equiv y\pmod 11\\
N\equiv z\pmod 13
\end{align*}
The Chinese Remainder Theorem tells us that for every $x$, $y$, and $z$, there is exactly one residue class modulo $7\cdot11\cdot13=1001$ such that the numbers $N$ in this residue class simultaneously solve
\begin{align*}
N\equiv x\pmod 7\\
N\equiv y\pmod 11\\
N\equiv z\pmod 13
\end{align*}
copeland
2012-03-30 21:00:51
What does this tell us about the number of integers from 1-1001that are simultaneously 7-safe, 11-safe, and 13-safe?
What does this tell us about the number of integers from 1-1001that are simultaneously 7-safe, 11-safe, and 13-safe?
alex31415
2012-03-30 21:02:40
There are 96 of them?
There are 96 of them?
danielguo94
2012-03-30 21:02:40
2*6*8 numbers
2*6*8 numbers
mcdonalds106_7
2012-03-30 21:02:40
there are 2*6*8 of them
there are 2*6*8 of them
sonchecky
2012-03-30 21:02:40
There are 2 * 6 * 8 = 96 between 1 and 1001.
There are 2 * 6 * 8 = 96 between 1 and 1001.
admin25
2012-03-30 21:02:40
There are 2*6*8=96
There are 2*6*8=96
numbertheorist17
2012-03-30 21:02:40
96
96
nackster12
2012-03-30 21:02:40
there are 2*6*8=96 of them
there are 2*6*8=96 of them
numberdance
2012-03-30 21:02:40
There are 2 (for 7)*6 (for 11)*8 (for 13) from 1-1001, so 96.
There are 2 (for 7)*6 (for 11)*8 (for 13) from 1-1001, so 96.
awesomemathlete
2012-03-30 21:02:40
there are 2*6*8
there are 2*6*8
Relativity1618
2012-03-30 21:02:40
they satisfy one of 96 linear congruences
they satisfy one of 96 linear congruences
CantonMathGuy
2012-03-30 21:02:40
2*6*8
2*6*8
brokenfixer
2012-03-30 21:02:40
there are 2 * 6 * 8 = 96 distinct possibilities from 1 ... 1001
there are 2 * 6 * 8 = 96 distinct possibilities from 1 ... 1001
copeland
2012-03-30 21:02:42
There are 2 choices (either 3 or 4) for the number's residue class mod 7. There are 6 choices (3-8) for the number's residue class mod 11. There are 8 choices (3-10) for the number's residue class mod 13. For each of these $2\cdot6\cdot8=96$ choices, there is exactly one number from 1 through 1001 that is 7-, 11-, and 13-safe (we'll call these numbers safe.
There are 2 choices (either 3 or 4) for the number's residue class mod 7. There are 6 choices (3-8) for the number's residue class mod 11. There are 8 choices (3-10) for the number's residue class mod 13. For each of these $2\cdot6\cdot8=96$ choices, there is exactly one number from 1 through 1001 that is 7-, 11-, and 13-safe (we'll call these numbers safe.
copeland
2012-03-30 21:02:46
What else?
What else?
alex31415
2012-03-30 21:04:10
there are 960 of them from 1-10010
there are 960 of them from 1-10010
brokenfixer
2012-03-30 21:04:10
they repeat every 1001
they repeat every 1001
nackster12
2012-03-30 21:04:10
from 1-10010 there are 96*10=960 safe numbers
from 1-10010 there are 96*10=960 safe numbers
PERFECTION
2012-03-30 21:04:10
from 1 to 10010, there are 960 numbers that match the conditions
from 1 to 10010, there are 960 numbers that match the conditions
admin25
2012-03-30 21:04:10
This repeats for the next multiples of 1001, so there are 96*10=960 through 10010
This repeats for the next multiples of 1001, so there are 96*10=960 through 10010
mcdonalds106_7
2012-03-30 21:04:10
so there are 960 from 1 to 10010... now cut out the end cases
so there are 960 from 1 to 10010... now cut out the end cases
copeland
2012-03-30 21:04:14
The same holds for 1002-2002. There are 96 safe integers in this interval as well.
The same holds for 1002-2002. There are 96 safe integers in this interval as well.
copeland
2012-03-30 21:04:17
There are 96 safe integers in each of the intervals 2003-3003, 3004-4004, all the way up to 8009-9009, and 9010-10010.
There are 96 safe integers in each of the intervals 2003-3003, 3004-4004, all the way up to 8009-9009, and 9010-10010.
copeland
2012-03-30 21:04:21
The first 9 intervals give us $9\cdot96$ total safe integers. However the last interval is only a partial interval. How can we count the number of safe integers in 9010-10000?
The first 9 intervals give us $9\cdot96$ total safe integers. However the last interval is only a partial interval. How can we count the number of safe integers in 9010-10000?
googol.plex
2012-03-30 21:05:27
subtract the ones from 10000-10010
subtract the ones from 10000-10010
GeorgiaTechMan
2012-03-30 21:05:27
just count the numbers from 10001-10010 that are p-safe and take 96- that number
just count the numbers from 10001-10010 that are p-safe and take 96- that number
CantonMathGuy
2012-03-30 21:05:27
subtract ones from 10000-10010
subtract ones from 10000-10010
brokenfixer
2012-03-30 21:05:27
find the safe integers in 10,001 to 10,010.
find the safe integers in 10,001 to 10,010.
sonchecky
2012-03-30 21:05:27
Go through 9010 - 10010 and then subtract out the extra ones above 10,000
Go through 9010 - 10010 and then subtract out the extra ones above 10,000
ABCDE
2012-03-30 21:05:27
subtract the number of safe integers in 10000-10010
subtract the number of safe integers in 10000-10010
nackster12
2012-03-30 21:05:27
960 minus the number of safe numbers in [10001, 10010]
960 minus the number of safe numbers in [10001, 10010]
copeland
2012-03-30 21:05:31
We know that there are 96 safe integers in 9010-10010. All we need to do is subtract the safe integers from 10001 to 10010.
We know that there are 96 safe integers in 9010-10010. All we need to do is subtract the safe integers from 10001 to 10010.
copeland
2012-03-30 21:05:34
Is 10010 safe?
Is 10010 safe?
himym83
2012-03-30 21:06:11
no, multiple of 1001
no, multiple of 1001
wmcho1007
2012-03-30 21:06:11
uh. no.
uh. no.
coldsummer
2012-03-30 21:06:11
NO WAY!!!!!!!!!!!!!!!!11
NO WAY!!!!!!!!!!!!!!!!11
-Transcend-
2012-03-30 21:06:11
no
no
lucylai
2012-03-30 21:06:11
nope
nope
numberdance
2012-03-30 21:06:11
No -- it's divisible by all of 7, 11, and 13.
No -- it's divisible by all of 7, 11, and 13.
nackster12
2012-03-30 21:06:11
no its divisible by 7, 11, and 13
no its divisible by 7, 11, and 13
awesomemathlete
2012-03-30 21:06:11
of course not
of course not
copeland
2012-03-30 21:06:12
No! This is a multiple of all 3.
No! This is a multiple of all 3.
copeland
2012-03-30 21:06:15
Is 10009 safe?
Is 10009 safe?
adamdai97
2012-03-30 21:07:06
noo
noo
sinnoel
2012-03-30 21:07:06
No
No
heliootrope
2012-03-30 21:07:06
No, it's too close to 10010
No, it's too close to 10010
mathnerd101
2012-03-30 21:07:06
no it is one less than a multiple of 7, 11, 13
no it is one less than a multiple of 7, 11, 13
admin25
2012-03-30 21:07:06
no, too close to 10010
no, too close to 10010
Relativity1618
2012-03-30 21:07:06
within 1 of a multiple of all 3
within 1 of a multiple of all 3
alex31415
2012-03-30 21:07:06
No, it is dangerous to 7
No, it is dangerous to 7
nackster12
2012-03-30 21:07:06
no, it's congruent to 6 modulo 7
no, it's congruent to 6 modulo 7
copeland
2012-03-30 21:07:13
No. This is within 1 of each of them.
No. This is within 1 of each of them.
copeland
2012-03-30 21:07:16
Now is a good time for a table:
Now is a good time for a table:
copeland
2012-03-30 21:07:20


copeland
2012-03-30 21:07:22
Which of these numbers are safe?
Which of these numbers are safe?
Relativity1618
2012-03-30 21:08:10
10006 and 10007
10006 and 10007
himym83
2012-03-30 21:08:10
10006, 10007
10006, 10007
mathnerd101
2012-03-30 21:08:10
10007 and 10008
10007 and 10008
vjnmath
2012-03-30 21:08:10
1006,1007
1006,1007
linpaws
2012-03-30 21:08:10
10006 and 10007
10006 and 10007
admin25
2012-03-30 21:08:10
10006 and 10007
10006 and 10007
coldsummer
2012-03-30 21:08:10
10007, 10006,
10007, 10006,
zinko1991
2012-03-30 21:08:10
10007, 10006
10007, 10006
MNL9082
2012-03-30 21:08:10
10006 10007
10006 10007
copeland
2012-03-30 21:08:15

copeland
2012-03-30 21:08:17
Only 2 of the numbers are safe. How many total safe numbers are there from 1 to 10000?
Only 2 of the numbers are safe. How many total safe numbers are there from 1 to 10000?
sonchecky
2012-03-30 21:09:18
960 - 2 = 958
960 - 2 = 958
Tuxianeer
2012-03-30 21:09:18
958
958
19oshawott98
2012-03-30 21:09:18
958!!
958!!
Relativity1618
2012-03-30 21:09:18
960-2=958
960-2=958
matholympiad25
2012-03-30 21:09:18
96*10-2=958
96*10-2=958
ahaanomegas
2012-03-30 21:09:18
958
958
loserboy
2012-03-30 21:09:18
958
958
hodgeheg
2012-03-30 21:09:18
There are 960-2=958 safe numbers. HOORAY... I understood the question
There are 960-2=958 safe numbers. HOORAY... I understood the question
bojobo
2012-03-30 21:09:18
958
958
copeland
2012-03-30 21:09:25
There are $9\cdot96+96-2=\boxed{958}$ total safe numbers through 10000.
There are $9\cdot96+96-2=\boxed{958}$ total safe numbers through 10000.
ptes77
2012-03-30 21:09:49
3 to go.
3 to go.
copeland
2012-03-30 21:09:52
Phew.
Phew.
copeland
2012-03-30 21:10:13
13. Equilateral $\triangle ABC$ has side length $\sqrt{111}$. There are four distinct triangles $AD_1 E_1$, $AD_1 E_2$, $AD_2 E_3$, and $AD_2 E_4$, each congruent to $\triangle ABC$, with $BD_1 = BD_2 = \sqrt{11}$. Find $\displaystyle \sum_{k = 1}^4 (CE_k)^2$.
13. Equilateral $\triangle ABC$ has side length $\sqrt{111}$. There are four distinct triangles $AD_1 E_1$, $AD_1 E_2$, $AD_2 E_3$, and $AD_2 E_4$, each congruent to $\triangle ABC$, with $BD_1 = BD_2 = \sqrt{11}$. Find $\displaystyle \sum_{k = 1}^4 (CE_k)^2$.
copeland
2012-03-30 21:10:30
Where do we start?
Where do we start?
GoldenFrog1618
2012-03-30 21:11:08
Since Phi_6(x) is the largest quadratic cyclotomic polynomial, can mobious transformations only have a period of 1 or 3?
Since Phi_6(x) is the largest quadratic cyclotomic polynomial, can mobious transformations only have a period of 1 or 3?
edisonchew240
2012-03-30 21:11:08
Diagram
Diagram
ABCDE
2012-03-30 21:11:08
draw a diagram but look at the triangles separately
draw a diagram but look at the triangles separately
Mary_Posa
2012-03-30 21:11:08
draw a diagram!
draw a diagram!
coldsummer
2012-03-30 21:11:08
diagram?
diagram?
brokenfixer
2012-03-30 21:11:08
draw a picture
draw a picture
Tuxianeer
2012-03-30 21:11:08
diagram
diagram
numbertheorist17
2012-03-30 21:11:08
diagram
diagram
copeland
2012-03-30 21:11:12
We should draw a picture.
We should draw a picture.
copeland
2012-03-30 21:11:17

copeland
2012-03-30 21:11:19
That's our first triangle. Where are the points $D_1$ and $D_2$?
That's our first triangle. Where are the points $D_1$ and $D_2$?
mathswimmer
2012-03-30 21:12:38
they all share point A and have same sidelengths-> circle and rotation
they all share point A and have same sidelengths-> circle and rotation
herro66
2012-03-30 21:12:38
equidistant from B
equidistant from B
ABCDE
2012-03-30 21:12:38
draw circle with center c and radius sqrt(111) and circle with center b with radius sqrt(11) and D_1 and D_2 are the intersections
draw circle with center c and radius sqrt(111) and circle with center b with radius sqrt(11) and D_1 and D_2 are the intersections
coldsummer
2012-03-30 21:12:38
on a circle with radius 11^1/2 with center B?
on a circle with radius 11^1/2 with center B?
brokenfixer
2012-03-30 21:12:38
draw circle around A of radius sqrt(111)
draw circle around A of radius sqrt(111)
sonchecky
2012-03-30 21:12:38
$sqrt(11)$ units away from B on separate arcs around C and A
$sqrt(11)$ units away from B on separate arcs around C and A
copeland
2012-03-30 21:12:41
These two points are on the circle of radius $\sqrt{11}$ centered at $B$, and they are also a distance of $\sqrt{111}$ from $A$. Therefore these two points are the intersection points of the circles of radius $\sqrt{11}$ and $\sqrt{111}$ centered at $B$ and $A$ respectively.
These two points are on the circle of radius $\sqrt{11}$ centered at $B$, and they are also a distance of $\sqrt{111}$ from $A$. Therefore these two points are the intersection points of the circles of radius $\sqrt{11}$ and $\sqrt{111}$ centered at $B$ and $A$ respectively.
copeland
2012-03-30 21:12:46


copeland
2012-03-30 21:12:48
Now we just draw equilateral triangles.
Now we just draw equilateral triangles.
copeland
2012-03-30 21:12:53

copeland
2012-03-30 21:12:59
Wow. Inscrutable. Let's focus on just one of those triangles:
Wow. Inscrutable. Let's focus on just one of those triangles:
copeland
2012-03-30 21:13:05

copeland
2012-03-30 21:13:08
How can we compute the distance $CE_1$?
How can we compute the distance $CE_1$?
GeorgiaTechMan
2012-03-30 21:13:54
that's easy. sqrt11!
that's easy. sqrt11!
edisonchew240
2012-03-30 21:13:54
CE_{1}=BD_{1}
CE_{1}=BD_{1}
brokenfixer
2012-03-30 21:13:54
BD1
BD1
Tuxianeer
2012-03-30 21:13:54
it is sqrt(11)
it is sqrt(11)
ABCDE
2012-03-30 21:13:54
it's symetrical so it's equal to BD_1 so sqrt(11)
it's symetrical so it's equal to BD_1 so sqrt(11)
GeorgiaTechMan
2012-03-30 21:13:54
ACE1 similar to ABD1
ACE1 similar to ABD1
heliootrope
2012-03-30 21:13:54
it's rotated the same distance away from C as D_1 is from B
it's rotated the same distance away from C as D_1 is from B
nackster12
2012-03-30 21:13:54
its just sqrt(11) since ABD_1 is congruent to ACE_1
its just sqrt(11) since ABD_1 is congruent to ACE_1
sonchecky
2012-03-30 21:13:54
$CE_1 = BD_1 = \sqrt(11)$
$CE_1 = BD_1 = \sqrt(11)$
herro66
2012-03-30 21:13:54
its sqrt{11}
its sqrt{11}
copeland
2012-03-30 21:13:57
This one's easy! $CE_1$ is equal to $BD_1$, since these two triangles are related by a rotation by some angle. The triangles $BAD_1$ and $CAE_1$ are SAS congruent, so
This one's easy! $CE_1$ is equal to $BD_1$, since these two triangles are related by a rotation by some angle. The triangles $BAD_1$ and $CAE_1$ are SAS congruent, so
copeland
2012-03-30 21:14:05
$CE_1^2=BD_1^2=11$.
$CE_1^2=BD_1^2=11$.
copeland
2012-03-30 21:14:10
Let's actually give this angle a name, since it looks like it's going to be important. Let $\theta=\angle CAE_1$.
Let's actually give this angle a name, since it looks like it's going to be important. Let $\theta=\angle CAE_1$.
copeland
2012-03-30 21:14:15
Good. Maybe the others will be this easy, too.
Good. Maybe the others will be this easy, too.
copeland
2012-03-30 21:14:20

copeland
2012-03-30 21:14:25
Or maybe not. . .
Or maybe not. . .
copeland
2012-03-30 21:14:29
What can we use to compute this distance?
What can we use to compute this distance?
himym83
2012-03-30 21:14:55
law of cosines
law of cosines
theone142857
2012-03-30 21:14:55
law of cos
law of cos
Relativity1618
2012-03-30 21:14:55
Law of Cosines
Law of Cosines
Duncanyang
2012-03-30 21:14:55
law of cosines
law of cosines
ahaanomegas
2012-03-30 21:14:55
Law of Cosines, maybe?
Law of Cosines, maybe?
eccfcco15
2012-03-30 21:14:55
law of cosines
law of cosines
alex31415
2012-03-30 21:14:55
law of cosines
law of cosines
copeland
2012-03-30 21:15:02
Since we have a lot of distances we know and angles we either know or can compute, it looks like the Law of Cosines could be very effective here.
Since we have a lot of distances we know and angles we either know or can compute, it looks like the Law of Cosines could be very effective here.
copeland
2012-03-30 21:15:24
We want $CE_2$ so we ought to think about $\triangle ACE_2$.
We want $CE_2$ so we ought to think about $\triangle ACE_2$.
copeland
2012-03-30 21:15:43
The Law of Cosines tells us that \[CE_2^2=AE_2^2+AC^2-2AE_2\cdot AC\cos\angle CAE_2.\]
The Law of Cosines tells us that \[CE_2^2=AE_2^2+AC^2-2AE_2\cdot AC\cos\angle CAE_2.\]
copeland
2012-03-30 21:15:47
All of those other lengths are known. In fact they're all $\sqrt{111}$. Therefore we have\[CE_2^2=111+111+2\cdot\sqrt{111}\sqrt{111}\cos\angle CAE_2\] so \[CE_2^2=222(1-\cos\angle CAE_2).\]
All of those other lengths are known. In fact they're all $\sqrt{111}$. Therefore we have\[CE_2^2=111+111+2\cdot\sqrt{111}\sqrt{111}\cos\angle CAE_2\] so \[CE_2^2=222(1-\cos\angle CAE_2).\]
copeland
2012-03-30 21:15:57
Another angle! Can we write $\angle CAE_2$ in terms of $\theta$?
Another angle! Can we write $\angle CAE_2$ in terms of $\theta$?
himym83
2012-03-30 21:17:13
120-theta
120-theta
ABCDE
2012-03-30 21:17:13
120-theta
120-theta
proglote
2012-03-30 21:17:13
yes, 120 - theta
yes, 120 - theta
nackster12
2012-03-30 21:17:13
120 degrees minus theta
120 degrees minus theta
sonchecky
2012-03-30 21:17:13
$120 - \theta$
$120 - \theta$
brokenfixer
2012-03-30 21:17:13
120 - theta i think
120 - theta i think
-Transcend-
2012-03-30 21:17:13
120-theta?
120-theta?
copeland
2012-03-30 21:17:21
Since $\theta=\angle BAD_1$, we know $\angle BAE_2=\frac\pi3-\theta$. Therefore \[\angle CAE_2=\angle CAB+\angle BAE_2=\frac\pi3+\frac\pi3-\theta.\]
Since $\theta=\angle BAD_1$, we know $\angle BAE_2=\frac\pi3-\theta$. Therefore \[\angle CAE_2=\angle CAB+\angle BAE_2=\frac\pi3+\frac\pi3-\theta.\]
copeland
2012-03-30 21:17:23
$CE_2^2=222(1-\cos(\tfrac{2\pi}3-\theta)).$
$CE_2^2=222(1-\cos(\tfrac{2\pi}3-\theta)).$
copeland
2012-03-30 21:17:35
I don't want to deal with that cosine yet. A lot of times in problems like these terms like that will cancel and we don't want to waste time. (Plus we can compare our expressions later and maybe find a mistake!)
I don't want to deal with that cosine yet. A lot of times in problems like these terms like that will cancel and we don't want to waste time. (Plus we can compare our expressions later and maybe find a mistake!)
copeland
2012-03-30 21:17:39
2 down. . . .
2 down. . . .
copeland
2012-03-30 21:17:49
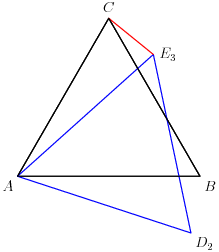

copeland
2012-03-30 21:18:05
Again we want the Law of Cosines. What is $\angle CAE_3$?
Again we want the Law of Cosines. What is $\angle CAE_3$?
sonchecky
2012-03-30 21:20:06
$\theta$
$\theta$
alex31415
2012-03-30 21:20:06
Is it the same as theta?
Is it the same as theta?
admin25
2012-03-30 21:20:06
it's equal to $ \angle BAD_2 $
it's equal to $ \angle BAD_2 $
numbertheorist17
2012-03-30 21:20:06
proglote
2012-03-30 21:20:06
isn't CE_3 = BD_2 = sqrt(11)?
isn't CE_3 = BD_2 = sqrt(11)?
numbertheorist17
2012-03-30 21:20:06
copeland
2012-03-30 21:20:09
Notice that $AD_1BD_2$ is a kite.
Notice that $AD_1BD_2$ is a kite.
copeland
2012-03-30 21:20:13


copeland
2012-03-30 21:20:25
Therefore $\angle CAD_2=\angle CAD_1=\theta$. By symmetry $\angle CAE_3=\angle BAD_2=\theta$.
Therefore $\angle CAD_2=\angle CAD_1=\theta$. By symmetry $\angle CAE_3=\angle BAD_2=\theta$.
copeland
2012-03-30 21:20:35
The LOC was a red herring.
The LOC was a red herring.
copeland
2012-03-30 21:20:36
We again have congruence, $\triangle CAE_3\cong \triangle BAD_2$, so
We again have congruence, $\triangle CAE_3\cong \triangle BAD_2$, so
copeland
2012-03-30 21:20:39
$CE_3^2=BD_2^2=11$.
$CE_3^2=BD_2^2=11$.
copeland
2012-03-30 21:21:09
One more;
One more;
copeland
2012-03-30 21:21:12

copeland
2012-03-30 21:21:14
Finally, $CE_4$. What is $\angle CAE_4$?
Finally, $CE_4$. What is $\angle CAE_4$?
himym83
2012-03-30 21:22:11
120+theta
120+theta
heliootrope
2012-03-30 21:22:11
120 + theta
120 + theta
ABCDE
2012-03-30 21:22:11
120+theta
120+theta
proglote
2012-03-30 21:22:11
120 + theta
120 + theta
-Transcend-
2012-03-30 21:22:11
120 + theta
120 + theta
sonchecky
2012-03-30 21:22:11
$120 + \theta$
$120 + \theta$
adamdai97
2012-03-30 21:22:11
120+theta
120+theta
Tuxianeer
2012-03-30 21:22:11
120+theta
120+theta
nackster12
2012-03-30 21:22:11
120+theta
120+theta
copeland
2012-03-30 21:22:14
$\angle CAE_4=\angle CAB+\angle BAD_2+\angle D_2AE_4=\frac{2\pi}3+\theta.$ Therefore
$\angle CAE_4=\angle CAB+\angle BAD_2+\angle D_2AE_4=\frac{2\pi}3+\theta.$ Therefore
copeland
2012-03-30 21:22:19
$CE_4^2=222(1-\cos(\tfrac{2\pi}3+\theta)).$
$CE_4^2=222(1-\cos(\tfrac{2\pi}3+\theta)).$
copeland
2012-03-30 21:22:24
When we add these four values we get
When we add these four values we get
copeland
2012-03-30 21:23:27
\begin{align*}CE_1^2+CE_2^2&+CE_3^2+CE_4^2=11+11\\&+222(1-\cos(\tfrac{2\pi}3-\theta))+222(1-\cos(\tfrac{2\pi}3+\theta)).\end{align*}
\begin{align*}CE_1^2+CE_2^2&+CE_3^2+CE_4^2=11+11\\&+222(1-\cos(\tfrac{2\pi}3-\theta))+222(1-\cos(\tfrac{2\pi}3+\theta)).\end{align*}
copeland
2012-03-30 21:23:31
$466-222(\cos(\tfrac{2\pi}3-\theta)+\cos(\tfrac{2\pi}3+\theta)).$
$466-222(\cos(\tfrac{2\pi}3-\theta)+\cos(\tfrac{2\pi}3+\theta)).$
Relativity1618
2012-03-30 21:23:52
now we use the sum to product formula
now we use the sum to product formula
theone142857
2012-03-30 21:23:52
2cos(2pi/3)cos(theta)
2cos(2pi/3)cos(theta)
brokenfixer
2012-03-30 21:23:52
cos(a+b) + cos(a-b)
cos(a+b) + cos(a-b)
Relativity1618
2012-03-30 21:23:52
sum to product formula
sum to product formula
copeland
2012-03-30 21:23:54
And. . .
And. . .
mathswimmer
2012-03-30 21:26:02
-cos(theta)
-cos(theta)
GeorgiaTechMan
2012-03-30 21:26:02
sorry, -cos(theta)
sorry, -cos(theta)
matholympiad25
2012-03-30 21:26:02
-cos theta
-cos theta
copeland
2012-03-30 21:26:07
We could use $\cos(x+y)+\cos(x-y)=2\cos x\cos y$, to write\[\cos(\tfrac{2\pi}3-\theta)+\cos(\tfrac{2\pi}3+\theta)=2\cos\tfrac{2\pi}3\cos\theta=-\cos\theta.\]
We could use $\cos(x+y)+\cos(x-y)=2\cos x\cos y$, to write\[\cos(\tfrac{2\pi}3-\theta)+\cos(\tfrac{2\pi}3+\theta)=2\cos\tfrac{2\pi}3\cos\theta=-\cos\theta.\]
copeland
2012-03-30 21:26:10
(Incidentally, this makes sense geometrically since the points $e^{i\theta}$, $e^{i(\theta+\frac{2\pi}3)}$ and $e^{i(\theta-\frac{2\pi}3)}$ are the vertices of an equilateral triangle with center of mass 0, so the real parts of these numbers must add to 0.)
(Incidentally, this makes sense geometrically since the points $e^{i\theta}$, $e^{i(\theta+\frac{2\pi}3)}$ and $e^{i(\theta-\frac{2\pi}3)}$ are the vertices of an equilateral triangle with center of mass 0, so the real parts of these numbers must add to 0.)
copeland
2012-03-30 21:26:21
$466+222\cos\theta.$
$466+222\cos\theta.$
copeland
2012-03-30 21:26:30
Hm. Of course we were going to have to figure something out about $\theta$. I guess now's the time. How can we find $\cos\theta$?
Hm. Of course we were going to have to figure something out about $\theta$. I guess now's the time. How can we find $\cos\theta$?
GeorgiaTechMan
2012-03-30 21:26:57
and we can use law of cosines on the sqrt111 sqrt111 sqrt 11 triangle to find out what cos theta is!
and we can use law of cosines on the sqrt111 sqrt111 sqrt 11 triangle to find out what cos theta is!
ABCDE
2012-03-30 21:26:57
law of cosines
law of cosines
admin25
2012-03-30 21:26:57
LOC on $ BAD_1 $
LOC on $ BAD_1 $
himym83
2012-03-30 21:26:57
use law of cosines on sqrt(11), sqrt(111), sqrt(111) triangle
use law of cosines on sqrt(11), sqrt(111), sqrt(111) triangle
proglote
2012-03-30 21:26:57
law of cosines in triangle BAD_1
law of cosines in triangle BAD_1
copeland
2012-03-30 21:27:01
We use the Law of Cosines on $\triangle ABD_1$.
We use the Law of Cosines on $\triangle ABD_1$.
copeland
2012-03-30 21:27:06

copeland
2012-03-30 21:27:10
$\cos\theta=\frac{\sqrt{111}^2+\sqrt{111}^2-\sqrt{11}^2}{2\sqrt{111}\cdot\sqrt{111}}=\frac{111+111-11}{222}=\frac{211}{222}$.
$\cos\theta=\frac{\sqrt{111}^2+\sqrt{111}^2-\sqrt{11}^2}{2\sqrt{111}\cdot\sqrt{111}}=\frac{111+111-11}{222}=\frac{211}{222}$.
copeland
2012-03-30 21:27:15
So what is the sum?
So what is the sum?
numbertheorist17
2012-03-30 21:28:01
Ans. 677
Ans. 677
alex31415
2012-03-30 21:28:01
so 466+211=677, the answer
so 466+211=677, the answer
Duncanyang
2012-03-30 21:28:01
677
677
nackster12
2012-03-30 21:28:01
466+211=677
466+211=677
numbertheorist17
2012-03-30 21:28:01


proglote
2012-03-30 21:28:01
677
677
sonchecky
2012-03-30 21:28:01
$466-222(-211/222) = 466+211=677$
$466-222(-211/222) = 466+211=677$
edisonchew240
2012-03-30 21:28:01
Ans=466+211=677
Ans=466+211=677
numbertheorist17
2012-03-30 21:28:01
466+211=677
466+211=677
math-rules
2012-03-30 21:28:01
677
677
-Transcend-
2012-03-30 21:28:01
677
677
copeland
2012-03-30 21:28:04
The sum is $466+222\cdot{211}{222}=466+211=\boxed{677}$.
The sum is $466+222\cdot{211}{222}=466+211=\boxed{677}$.
copeland
2012-03-30 21:28:13
Phew, that was 13. We have 2 to go.
Phew, that was 13. We have 2 to go.
copeland
2012-03-30 21:28:18
Still trucking?
Still trucking?
brokenfixer
2012-03-30 21:28:52
in need of pudding
in need of pudding
mathnerd101
2012-03-30 21:28:52
man im hungry for pudding :P
man im hungry for pudding :P
copeland
2012-03-30 21:28:54
I THINK IT AND YOU SAY IT! AMAZING!
I THINK IT AND YOU SAY IT! AMAZING!
copeland
2012-03-30 21:29:08
14. In a group of nine people each person shakes hands with exactly two of the other people from the group. Let $N$ be the number of ways this handshaking can occur. Consider two handshaking arrangements to be different if and only if at least two people who shake hands under one arrangement do not shake hands under the other arrangement. Find the remainder when $N$ is divided by 1000.
14. In a group of nine people each person shakes hands with exactly two of the other people from the group. Let $N$ be the number of ways this handshaking can occur. Consider two handshaking arrangements to be different if and only if at least two people who shake hands under one arrangement do not shake hands under the other arrangement. Find the remainder when $N$ is divided by 1000.
GeorgiaTechMan
2012-03-30 21:29:23
whats up with pudding?
whats up with pudding?
copeland
2012-03-30 21:29:25
Pudding rules, yo.
Pudding rules, yo.
copeland
2012-03-30 21:29:37
Hmm. Again it's not clear what to do here, so where should we start?
Hmm. Again it's not clear what to do here, so where should we start?
mathnerd101
2012-03-30 21:30:21
picture?
picture?
Imsacred
2012-03-30 21:30:21
picture? at least thats what i did
picture? at least thats what i did
admin25
2012-03-30 21:30:21
draw a diagram?
draw a diagram?
ahaanomegas
2012-03-30 21:30:21
Read the problem at least 3 times. Process the words.
Read the problem at least 3 times. Process the words.
Titandrake
2012-03-30 21:30:21
draw some graphs?
draw some graphs?
copeland
2012-03-30 21:30:26
Yeah, let's draw some stuff.
Yeah, let's draw some stuff.
brokenfixer
2012-03-30 21:30:31
what's with the "consider handshakings different" clause?
what's with the "consider handshakings different" clause?
copeland
2012-03-30 21:30:47
Yeah, right? I read that 4 times before I decided it didn't say anything.
Yeah, right? I read that 4 times before I decided it didn't say anything.
copeland
2012-03-30 21:31:13
When I started drawing pictures, I decided that 9 was WAY too big and started with smaller numbers instead.
When I started drawing pictures, I decided that 9 was WAY too big and started with smaller numbers instead.
copeland
2012-03-30 21:31:28
So let's begin with a smaller example. Let $n$ be the number of people.
So let's begin with a smaller example. Let $n$ be the number of people.
copeland
2012-03-30 21:31:32
Let's start with $n=3$. How many ways are there for 3 people to shake hands where each person shakes hands with two others?
Let's start with $n=3$. How many ways are there for 3 people to shake hands where each person shakes hands with two others?
Tuxianeer
2012-03-30 21:32:08
1
1
heliootrope
2012-03-30 21:32:08
1
1
lucylai
2012-03-30 21:32:08
1
1
MathTwo
2012-03-30 21:32:08
1 way
1 way
proglote
2012-03-30 21:32:08
only one, each person shakes the hands of the other two
only one, each person shakes the hands of the other two
mcdonalds106_7
2012-03-30 21:32:08
1 way
1 way
copeland
2012-03-30 21:32:11
There's only one way to do this.
There's only one way to do this.
copeland
2012-03-30 21:32:16

copeland
2012-03-30 21:32:17
If $n=4$ how many ways are there to shake hands?
If $n=4$ how many ways are there to shake hands?
GeorgiaTechMan
2012-03-30 21:32:46
3
3
lucylai
2012-03-30 21:32:46
3
3
Duncanyang
2012-03-30 21:32:46
3
3
Tuxianeer
2012-03-30 21:32:46
3
3
brokenfixer
2012-03-30 21:32:46
two bowties and a loop?
two bowties and a loop?
nackster12
2012-03-30 21:32:46
3
3
admin25
2012-03-30 21:32:46
3, right?
3, right?
copeland
2012-03-30 21:32:51
Each person shakes hands with 2 people so he does not shake hands with one other person. There are 3 ways to match 4 people into pairs of uncordial pairs.
Each person shakes hands with 2 people so he does not shake hands with one other person. There are 3 ways to match 4 people into pairs of uncordial pairs.
copeland
2012-03-30 21:32:57


copeland
2012-03-30 21:33:01
What do you notice?
What do you notice?
admin25
2012-03-30 21:34:01
it's a closed loop?
it's a closed loop?
Imsacred
2012-03-30 21:34:01
or you can always represent this problem with a closed loop or a system of closed loops
or you can always represent this problem with a closed loop or a system of closed loops
copeland
2012-03-30 21:34:06
Since every person is connected to two other people, all of our graphs are "loops."
Since every person is connected to two other people, all of our graphs are "loops."
copeland
2012-03-30 21:34:10
By this we mean we start with some Person A. Person A shakes hand with Person B. Person B shakes hands with one other person, Person C. Person C shakes with one other person, Person D. Since there are only finitely many people, eventually we must come around to the other person who shook hands with Person A.
By this we mean we start with some Person A. Person A shakes hand with Person B. Person B shakes hands with one other person, Person C. Person C shakes with one other person, Person D. Since there are only finitely many people, eventually we must come around to the other person who shook hands with Person A.
copeland
2012-03-30 21:34:21
When $n=9$, will all of the graphs be loops?
When $n=9$, will all of the graphs be loops?
GeorgiaTechMan
2012-03-30 21:34:53
so we can either have 1 loop, 2 loops, or 3 loops
so we can either have 1 loop, 2 loops, or 3 loops
lucylai
2012-03-30 21:34:53
no there can be separate loops
no there can be separate loops
nackster12
2012-03-30 21:34:53
you could have multiple loops
you could have multiple loops
proglote
2012-03-30 21:34:53
there might be disjoint loops
there might be disjoint loops
copeland
2012-03-30 21:34:56
No, it's possible that the graph breaks into multiple loops:
No, it's possible that the graph breaks into multiple loops:
copeland
2012-03-30 21:35:01

copeland
2012-03-30 21:35:03
However all 9 of the people must be in some loop or other.
However all 9 of the people must be in some loop or other.
copeland
2012-03-30 21:35:07
The graph could be a single loop of all 9 people.
The graph could be a single loop of all 9 people.
copeland
2012-03-30 21:35:12
If the graph breaks into two loops, what are the possibilites for the number of people in each loop?
If the graph breaks into two loops, what are the possibilites for the number of people in each loop?
GeorgiaTechMan
2012-03-30 21:35:45
3 and 6, or 4 and 5
3 and 6, or 4 and 5
math-rules
2012-03-30 21:35:45
3-6, 4-5
3-6, 4-5
ABCDE
2012-03-30 21:35:45
4&5 or 3&6
4&5 or 3&6
heliootrope
2012-03-30 21:35:45
3 and 6 or 4 and 5 in some order
3 and 6 or 4 and 5 in some order
proglote
2012-03-30 21:35:45
(3,6) and (4,5)
(3,6) and (4,5)
Imsacred
2012-03-30 21:35:45
3 and 6 or 4 and 5
3 and 6 or 4 and 5
dantx5
2012-03-30 21:35:45
3 and 6, 4 and 5
3 and 6, 4 and 5
copeland
2012-03-30 21:35:49
Since every loop needs at least 3 people, two loops can be created with sizes 3 and 6 or 4 and 5.
Since every loop needs at least 3 people, two loops can be created with sizes 3 and 6 or 4 and 5.
copeland
2012-03-30 21:35:53
What about 3 loops?
What about 3 loops?
brokenfixer
2012-03-30 21:36:13
3 3 3
3 3 3
proglote
2012-03-30 21:36:13
only (3, 3, 3)
only (3, 3, 3)
ABCDE
2012-03-30 21:36:13
3, 3, 3
3, 3, 3
himym83
2012-03-30 21:36:13
3, 3, and 3
3, 3, and 3
alex31415
2012-03-30 21:36:13
3, 3, and 3
3, 3, and 3
adamdai97
2012-03-30 21:36:13
3,3,3
3,3,3
success
2012-03-30 21:36:13
3,3,3
3,3,3
copeland
2012-03-30 21:36:18
With three loops, all of the loops must be of size 3.
With three loops, all of the loops must be of size 3.
copeland
2012-03-30 21:36:21
Therefore we're down to our casework. We can either have a single loop of size 9, we can have two loops of sizes {6,3} or {5,4} or we could have three loops of sizes {3,3,3}.
Therefore we're down to our casework. We can either have a single loop of size 9, we can have two loops of sizes {6,3} or {5,4} or we could have three loops of sizes {3,3,3}.
copeland
2012-03-30 21:36:27
OK, good. Now we are set up to start counting.
OK, good. Now we are set up to start counting.
copeland
2012-03-30 21:36:32
How many possible ways are there for 9 people to shake hands in a single loop?
How many possible ways are there for 9 people to shake hands in a single loop?
GeorgiaTechMan
2012-03-30 21:37:48
8 factorial divided by 2
8 factorial divided by 2
GeorgiaTechMan
2012-03-30 21:37:48
or 20160
or 20160
ABCDE
2012-03-30 21:37:48
8!/2=20160
8!/2=20160
lucylai
2012-03-30 21:37:48
20,160
20,160
dantx5
2012-03-30 21:37:48
8!/2 ?
8!/2 ?
lucylai
2012-03-30 21:37:48
8!/2=20160
8!/2=20160
sonchecky
2012-03-30 21:37:48
8! / 2 = 20160
8! / 2 = 20160
copeland
2012-03-30 21:37:52
We can construct a loop of 9 people in the same way as we would place 9 people around a round table. There are $8!$ ways to create such an arrangement, and we count these by finding where Person 1 is sitting and placing the remaining 8 people relative to him in any permutation. However there's a difference here: our loops don't have orientation, so reversing the order of the table gives the same loop.
We can construct a loop of 9 people in the same way as we would place 9 people around a round table. There are $8!$ ways to create such an arrangement, and we count these by finding where Person 1 is sitting and placing the remaining 8 people relative to him in any permutation. However there's a difference here: our loops don't have orientation, so reversing the order of the table gives the same loop.
copeland
2012-03-30 21:37:58
There are $\frac{8!}2$ ways to create a single loop of people shaking hands.
There are $\frac{8!}2$ ways to create a single loop of people shaking hands.
copeland
2012-03-30 21:38:05
We can compute this completely, or notice that \[8\cdot7\cdot6\cdot5\cdot4\cdot3=(7\cdot3)(6\cdot8)(5\cdot4)=21\cdot48\cdot20=21\cdot960.\]
We can compute this completely, or notice that \[8\cdot7\cdot6\cdot5\cdot4\cdot3=(7\cdot3)(6\cdot8)(5\cdot4)=21\cdot48\cdot20=21\cdot960.\]
copeland
2012-03-30 21:38:12
We only care about this value mod 1000, so\[21\cdot960\equiv21\cdot(-40)\equiv-840\equiv160\pmod{1000}.\]
We only care about this value mod 1000, so\[21\cdot960\equiv21\cdot(-40)\equiv-840\equiv160\pmod{1000}.\]
copeland
2012-03-30 21:38:23
How many ways are there to create a pair of loops if one has size 3 and the other has size 6?
How many ways are there to create a pair of loops if one has size 3 and the other has size 6?
copeland
2012-03-30 21:39:42
Hmm. Maybe that's too many steps at once.
Hmm. Maybe that's too many steps at once.
copeland
2012-03-30 21:39:48
First how many ways can we form the group of 3?
First how many ways can we form the group of 3?
-Transcend-
2012-03-30 21:40:23
9 choose 3
9 choose 3
brokenfixer
2012-03-30 21:40:23
9 choose 3
9 choose 3
himym83
2012-03-30 21:40:23
9C3
9C3
Duncanyang
2012-03-30 21:40:23
9 choose 3
9 choose 3
dantx5
2012-03-30 21:40:23
9 C 3
9 C 3
ABCDE
2012-03-30 21:40:23
9C3=84
9C3=84
math-rules
2012-03-30 21:40:23
9c3=84
9c3=84
proglote
2012-03-30 21:40:23
9C3 = 84
9C3 = 84
Tuxianeer
2012-03-30 21:40:23
9C3=84
9C3=84
wmcho1007
2012-03-30 21:40:26
9*8*7/6=84
9*8*7/6=84
copeland
2012-03-30 21:40:34
First we pick which people will be in the loop of size 3. There are $\binom93$ ways to do this.
First we pick which people will be in the loop of size 3. There are $\binom93$ ways to do this.
copeland
2012-03-30 21:40:46
Once we make that choice, we need to arrange the remaining people into a loop of 6.
Once we make that choice, we need to arrange the remaining people into a loop of 6.
copeland
2012-03-30 21:40:51
How many ways are there to do that?
How many ways are there to do that?
brokenfixer
2012-03-30 21:41:20
2!/2 * 5!/2 which is 5*4*3 = 60 ways
2!/2 * 5!/2 which is 5*4*3 = 60 ways
Tuxianeer
2012-03-30 21:41:20
1 way to loop group of 3, and 5!/2=60 WAYS FOR THE GROUP OF 6
1 way to loop group of 3, and 5!/2=60 WAYS FOR THE GROUP OF 6
lucylai
2012-03-30 21:41:20
5!/2=60
5!/2=60
himym83
2012-03-30 21:41:20
5!/2
5!/2
GeorgiaTechMan
2012-03-30 21:41:20
5!/2=60
5!/2=60
nackster12
2012-03-30 21:41:20
5!/2=60
5!/2=60
proglote
2012-03-30 21:41:20
5!/2 = 60
5!/2 = 60
copeland
2012-03-30 21:41:35
Once the trio has been chosen, there are $\frac{5!}2$ ways to organize the subgroup of 6 people and only $\frac{2!}2=1$ way to arrange the subgroup of size 3.
Once the trio has been chosen, there are $\frac{5!}2$ ways to organize the subgroup of 6 people and only $\frac{2!}2=1$ way to arrange the subgroup of size 3.
copeland
2012-03-30 21:41:40
There are $\binom93\cdot\frac{5!}2\cdot1=\frac{9!5!}{2\cdot3!6!}$ ways to organize 9 people into a loop of size 6 and a loop of size 3.
There are $\binom93\cdot\frac{5!}2\cdot1=\frac{9!5!}{2\cdot3!6!}$ ways to organize 9 people into a loop of size 6 and a loop of size 3.
copeland
2012-03-30 21:41:45
Again for some arithmetic. This one is easy enough to compute directly:\[\frac{(9\cdot8\cdot7)(5\cdot4)}2=72\cdot7\cdot10=5040.\]So we get another \[5040\equiv40\pmod{1000}.\]
Again for some arithmetic. This one is easy enough to compute directly:\[\frac{(9\cdot8\cdot7)(5\cdot4)}2=72\cdot7\cdot10=5040.\]So we get another \[5040\equiv40\pmod{1000}.\]
copeland
2012-03-30 21:41:51
Likewise there are $\binom94\cdot\frac{4!}2\cdot\frac{3!}2=\frac{9!4!3!}{2\cdot2\cdot5!\cdot4!}$ ways to organize 9 people into a loop of size 5 and a loop of size 4.
Likewise there are $\binom94\cdot\frac{4!}2\cdot\frac{3!}2=\frac{9!4!3!}{2\cdot2\cdot5!\cdot4!}$ ways to organize 9 people into a loop of size 5 and a loop of size 4.
copeland
2012-03-30 21:42:05
$\frac{9!4!3!}{2\cdot2\cdot5!\cdot4!}=\frac{9\cdot8\cdot7\cdot6\cdot3}2=(9\cdot6)(7\cdot3)\cdot\frac82=54\cdot21\cdot4=1134\cdot4.$
$\frac{9!4!3!}{2\cdot2\cdot5!\cdot4!}=\frac{9\cdot8\cdot7\cdot6\cdot3}2=(9\cdot6)(7\cdot3)\cdot\frac82=54\cdot21\cdot4=1134\cdot4.$
copeland
2012-03-30 21:42:10
Mod 1000 we get $1134\cdot4\equiv134\cdot4=536\pmod{1000}.$
Mod 1000 we get $1134\cdot4\equiv134\cdot4=536\pmod{1000}.$
copeland
2012-03-30 21:42:40
What about three loops of size 3? How many ways can we organize 9 people into such groups?
What about three loops of size 3? How many ways can we organize 9 people into such groups?
himym83
2012-03-30 21:44:13
9C3 * 6C3 * 3C3/3!
9C3 * 6C3 * 3C3/3!
nackster12
2012-03-30 21:44:13
9C3*6C3/3!
9C3*6C3/3!
ABCDE
2012-03-30 21:44:13
9C3*6C3/6
9C3*6C3/6
-Transcend-
2012-03-30 21:44:13
9C3 * 6C3 / 3! ?
9C3 * 6C3 / 3! ?
wmcho1007
2012-03-30 21:44:21
(9C3*6C3*3C3)/6
(9C3*6C3*3C3)/6
brokenfixer
2012-03-30 21:44:21
9C3 * 6C3 / 3!
9C3 * 6C3 / 3!
copeland
2012-03-30 21:44:22
We can paint the 9 people in three colors in $\binom 96\cdot\binom63$ ways. however the colors are irrelevant so we need to divide by $3!$ to handle overcounting.
We can paint the 9 people in three colors in $\binom 96\cdot\binom63$ ways. however the colors are irrelevant so we need to divide by $3!$ to handle overcounting.
copeland
2012-03-30 21:45:12
There is a total of $\frac{9\cdot8\cdot7\cdot6\cdot5\cdot4}{3!\cdot3!\cdot3!}=\frac{8\cdot7\cdot5\cdot4}{2\cdot2}=280$ ways for the 9 people to be partitioned into groups of 3.
There is a total of $\frac{9\cdot8\cdot7\cdot6\cdot5\cdot4}{3!\cdot3!\cdot3!}=\frac{8\cdot7\cdot5\cdot4}{2\cdot2}=280$ ways for the 9 people to be partitioned into groups of 3.
copeland
2012-03-30 21:45:26
Our grand total is $160+40+536+280\equiv016\pmod{1000}.$
Our grand total is $160+40+536+280\equiv016\pmod{1000}.$
copeland
2012-03-30 21:45:32
The answer is $\boxed{016}$.
The answer is $\boxed{016}$.
ahaanomegas
2012-03-30 21:45:38
Therefore, our answer is 016.
Therefore, our answer is 016.
copeland
2012-03-30 21:45:40
Whee!
Whee!
copeland
2012-03-30 21:45:52
Hey, guess what?
Hey, guess what?
Fire-Sword
2012-03-30 21:46:12
time for the last one
time for the last one
19oshawott98
2012-03-30 21:46:12
LAAST PROBLEM!!!!
LAAST PROBLEM!!!!
-Transcend-
2012-03-30 21:46:12
Last one!
Last one!
numbertheorist17
2012-03-30 21:46:12
pudding is good
pudding is good
alex31415
2012-03-30 21:46:12
Last Problem!
Last Problem!
brokenfixer
2012-03-30 21:46:12
pudding!
pudding!
nackster12
2012-03-30 21:46:12
last question!
last question!
ahaanomegas
2012-03-30 21:46:12
Last one, best one.
Last one, best one.
mcdonalds106_7
2012-03-30 21:46:12
Last problem~
Last problem~
-Transcend-
2012-03-30 21:46:12
You like pudding?
You like pudding?
Duncanyang
2012-03-30 21:46:12
one more problem to go!!!!
one more problem to go!!!!
MathTwo
2012-03-30 21:46:12
we have one problem left!
we have one problem left!
copeland
2012-03-30 21:46:18
Yeah, last problem.
Yeah, last problem.
copeland
2012-03-30 21:46:29
copeland
2012-03-30 21:46:47
We'll start with a diagram:
We'll start with a diagram:
copeland
2012-03-30 21:46:53
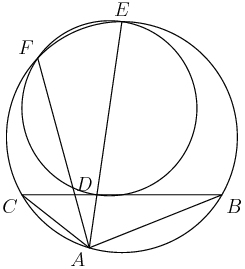

copeland
2012-03-30 21:47:00
That's clearly not enough. Do we know anything interesting about $E$ or $F?$
That's clearly not enough. Do we know anything interesting about $E$ or $F?$
numbertheorist17
2012-03-30 21:48:27
equilateral triangle
equilateral triangle
admin25
2012-03-30 21:48:27
EB=EC
EB=EC
proglote
2012-03-30 21:48:27
E is in the perpendicular bisector of BC
E is in the perpendicular bisector of BC
GeorgiaTechMan
2012-03-30 21:48:27
we can also do angle bisector and stewarts and then figure out EBC is equilateral.
we can also do angle bisector and stewarts and then figure out EBC is equilateral.
sonchecky
2012-03-30 21:48:27
BEC is an equilateral triangle.
BEC is an equilateral triangle.
copeland
2012-03-30 21:48:31
We know that $E$ is the midpoint of arc $BEC,$ since $AE$ bisects $\angle CAB.$
We know that $E$ is the midpoint of arc $BEC,$ since $AE$ bisects $\angle CAB.$
copeland
2012-03-30 21:48:45
Let's keep that in mind.
Let's keep that in mind.
copeland
2012-03-30 21:48:55
What other point wants to be labeled?
What other point wants to be labeled?
Duncanyang
2012-03-30 21:50:22
they interstctions.
they interstctions.
dantx5
2012-03-30 21:50:22
bottom of small circle?
bottom of small circle?
math-rules
2012-03-30 21:50:22
intersection of AF and smaller circle
intersection of AF and smaller circle
copeland
2012-03-30 21:50:31
OK, that's two suggestions of points that are already on the diagram.
OK, that's two suggestions of points that are already on the diagram.
copeland
2012-03-30 21:50:50
I like the point on CB because it has more to do with the things we know (ABC).
I like the point on CB because it has more to do with the things we know (ABC).
copeland
2012-03-30 21:50:59
We will think about the other point where the little circle hits $BC.$ Let's call that $M.$
We will think about the other point where the little circle hits $BC.$ Let's call that $M.$
copeland
2012-03-30 21:51:04
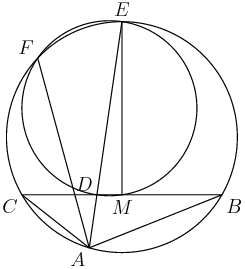

copeland
2012-03-30 21:51:07
Let's think about the little circle for a second.
Let's think about the little circle for a second.
copeland
2012-03-30 21:51:11

copeland
2012-03-30 21:51:19
Does the little circle tell us anything interesting about $M?$
Does the little circle tell us anything interesting about $M?$
Duncanyang
2012-03-30 21:52:00
EM perpendicular to CB
EM perpendicular to CB
brokenfixer
2012-03-30 21:52:00
EMD is right
EMD is right
himym83
2012-03-30 21:52:00
angle EMD is 90
angle EMD is 90
Fire-Sword
2012-03-30 21:52:00
ummm its perpendicular to CB?
ummm its perpendicular to CB?
admin25
2012-03-30 21:52:00
$ \angle EDM=90^\circ $
$ \angle EDM=90^\circ $
adamdai97
2012-03-30 21:52:00
EDM is right
EDM is right
brokenfixer
2012-03-30 21:52:00
EM is perpendicular to BC because EMD is right angle
EM is perpendicular to BC because EMD is right angle
heliootrope
2012-03-30 21:52:02
EMD is right
EMD is right
copeland
2012-03-30 21:52:05
We know that $\angle EMD$ is a right angle because $ED$ is a diameter of the small circle. So?
We know that $\angle EMD$ is a right angle because $ED$ is a diameter of the small circle. So?
numbertheorist17
2012-03-30 21:52:46
M is midpoint?
M is midpoint?
MathTwo
2012-03-30 21:52:46
M is the midpoint of BC
M is the midpoint of BC
sonchecky
2012-03-30 21:52:46
M is the midpoint of BC
M is the midpoint of BC
proglote
2012-03-30 21:52:46
so M is the midpoint of BC
so M is the midpoint of BC
admin25
2012-03-30 21:52:46
so EM is perpendicular to BC!
so EM is perpendicular to BC!
brokenfixer
2012-03-30 21:52:46
EM is perpendicular bisector to BC
EM is perpendicular bisector to BC
copeland
2012-03-30 21:52:52
Since $E$ is the midpoint of arc $BEC$ and $EM$ is perpendicular to $BC,$ we know that $EM$ bisects chord $BC.$ That is, $M$ is the midpoint of $BC.$
Since $E$ is the midpoint of arc $BEC$ and $EM$ is perpendicular to $BC,$ we know that $EM$ bisects chord $BC.$ That is, $M$ is the midpoint of $BC.$
copeland
2012-03-30 21:52:56
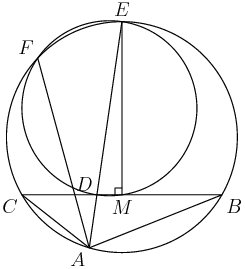

copeland
2012-03-30 21:53:01
We've stumbled on a couple interesting facts here: that $\angle EMD$ is a right angle, and that $M$ is the midpoint of $BC.$ When we stumble on interesting facts, we should check out where they lead. Where might we go from here?
We've stumbled on a couple interesting facts here: that $\angle EMD$ is a right angle, and that $M$ is the midpoint of $BC.$ When we stumble on interesting facts, we should check out where they lead. Where might we go from here?
GeorgiaTechMan
2012-03-30 21:54:24
DFE is right?
DFE is right?
admin25
2012-03-30 21:54:24
The center of the large circle lies on EM?
The center of the large circle lies on EM?
dantx5
2012-03-30 21:54:24
draw diameter of big circle
draw diameter of big circle
copeland
2012-03-30 21:54:29
There are a couple directions we could go. First, seeing the right angle at $\angle EMD,$ we realize that there's a right angle at $\angle DFE,$ again because $ED$ is a diameter (or because FEMD is cyclic).
There are a couple directions we could go. First, seeing the right angle at $\angle EMD,$ we realize that there's a right angle at $\angle DFE,$ again because $ED$ is a diameter (or because FEMD is cyclic).
copeland
2012-03-30 21:54:40
Since $M$ is the midpoint of $BC$ and $E$ is the midpoint of arc $BEC,$ extending $EM$ to hit the large circle again gives us a diameter of the large circle:
Since $M$ is the midpoint of $BC$ and $E$ is the midpoint of arc $BEC,$ extending $EM$ to hit the large circle again gives us a diameter of the large circle:
copeland
2012-03-30 21:54:52
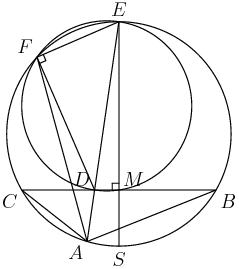

copeland
2012-03-30 21:55:00
What does this diagram make us wonder?
What does this diagram make us wonder?
proglote
2012-03-30 21:55:56
so F, D, S are collinear
so F, D, S are collinear
sonchecky
2012-03-30 21:55:56
if F, D, and S are collinear
if F, D, and S are collinear
eccfcco15
2012-03-30 21:56:01
are F, D, and S colinear
are F, D, and S colinear
brokenfixer
2012-03-30 21:56:01
does FD continue through S
does FD continue through S
copeland
2012-03-30 21:56:07
It sure looks like the extension of $FD$ hits $S.$ Does it?
It sure looks like the extension of $FD$ hits $S.$ Does it?
proglote
2012-03-30 21:57:05
yes, since EF is perpendicular to FD, it should hit the circle at the antipode of E, which is just S
yes, since EF is perpendicular to FD, it should hit the circle at the antipode of E, which is just S
himym83
2012-03-30 21:57:05
yes: EFS is a right angle since ES is the diameter
yes: EFS is a right angle since ES is the diameter
admin25
2012-03-30 21:57:05
ES is a diameter, EFD is a right angle, and F is on the circle, so yes!
ES is a diameter, EFD is a right angle, and F is on the circle, so yes!
sonchecky
2012-03-30 21:57:05
Yes because EFD is right so it must subtend a semicircle and the endpoints must be a diameter of the large circle
Yes because EFD is right so it must subtend a semicircle and the endpoints must be a diameter of the large circle
brokenfixer
2012-03-30 21:57:05
90 degree angle at F must hit both ends of the diameter ES
90 degree angle at F must hit both ends of the diameter ES
dantx5
2012-03-30 21:57:05
yes, because FED is a right angle, and ES is a diameter.
yes, because FED is a right angle, and ES is a diameter.
copeland
2012-03-30 21:57:09
Because $ES$ is a diameter of the large circle, $\angle EFS$ is a right angle. But we already know that $\angle EFD$ is right, so $D$ is on $FS:$
Because $ES$ is a diameter of the large circle, $\angle EFS$ is a right angle. But we already know that $\angle EFD$ is right, so $D$ is on $FS:$
copeland
2012-03-30 21:57:15

copeland
2012-03-30 21:57:24
We've found another surprise in that $EM$ and $FD$ meet on the circle at point $S,$ so we should investigate that point and how it relates to the rest of the diagram. See anything interesting?
We've found another surprise in that $EM$ and $FD$ meet on the circle at point $S,$ so we should investigate that point and how it relates to the rest of the diagram. See anything interesting?
copeland
2012-03-30 21:59:32
Several of you have found interesting similar triangles. These can be helpful for various tactics, but most of the suggestions give us relationships between unknown lengths.
Several of you have found interesting similar triangles. These can be helpful for various tactics, but most of the suggestions give us relationships between unknown lengths.
copeland
2012-03-30 21:59:37
Can we find any more right angles in here?
Can we find any more right angles in here?
himym83
2012-03-30 22:00:36
EAS
EAS
proglote
2012-03-30 22:00:36
EAS is right since F, E, A, S are concyclic
EAS is right since F, E, A, S are concyclic
sonchecky
2012-03-30 22:00:36
angle EAS
angle EAS
edisonchew240
2012-03-30 22:00:36
<EAS
<EAS
math-rules
2012-03-30 22:00:36
EAS is right
EAS is right
copeland
2012-03-30 22:00:40
Right angles lead to cyclic quadrilaterals and diameters lead to right angles. $\angle DMS = 90^\circ$, and $\angle SAE = 90^\circ$ because $ES$ is a diameter. $ADMS$ is cyclic!
Right angles lead to cyclic quadrilaterals and diameters lead to right angles. $\angle DMS = 90^\circ$, and $\angle SAE = 90^\circ$ because $ES$ is a diameter. $ADMS$ is cyclic!
copeland
2012-03-30 22:00:47

copeland
2012-03-30 22:00:54
Of course, we still haven't gotten around to $AF.$ We could chase and discover more stuff about this diagram (there's a lot of stuff lurking about), but it's not clear we're even getting closer to $AF.$ We have found lots of good stuff. At some point, we have to think about what we want, $AF,$ and focus our efforts. Let's try that now. We'd like to relate $AF$ to parts of the diagram that we know more about. What might we do to help us with that?
Of course, we still haven't gotten around to $AF.$ We could chase and discover more stuff about this diagram (there's a lot of stuff lurking about), but it's not clear we're even getting closer to $AF.$ We have found lots of good stuff. At some point, we have to think about what we want, $AF,$ and focus our efforts. Let's try that now. We'd like to relate $AF$ to parts of the diagram that we know more about. What might we do to help us with that?
copeland
2012-03-30 22:01:53
Triangles $AFD$ and $SED$ are similar, so we can relate $AF$ to $AD,$ $DF,$ and the sides of $SED.$ With a whole lot of effort, we can work out some of those lengths, but we sure would like to find something slicker to do. We'd prefer to relate AF to sides whose lengths we already know. What side lengths do we already know?
Triangles $AFD$ and $SED$ are similar, so we can relate $AF$ to $AD,$ $DF,$ and the sides of $SED.$ With a whole lot of effort, we can work out some of those lengths, but we sure would like to find something slicker to do. We'd prefer to relate AF to sides whose lengths we already know. What side lengths do we already know?
ABCDE
2012-03-30 22:02:52
AB BC and CA
AB BC and CA
proglote
2012-03-30 22:02:52
the side lengths of ABC
the side lengths of ABC
alex31415
2012-03-30 22:02:52
AC=3, AB=5, and BC=7
AC=3, AB=5, and BC=7
Tuxianeer
2012-03-30 22:02:52
AB=5,BC=7,AC=3
AB=5,BC=7,AC=3
copeland
2012-03-30 22:02:57
We know the side lengths of $\triangle ABC,$ we know $BM$ and $CM,$ and we can use the Angle Bisector Theorem to get at $DC$ and $DB.$
We know the side lengths of $\triangle ABC,$ we know $BM$ and $CM,$ and we can use the Angle Bisector Theorem to get at $DC$ and $DB.$
copeland
2012-03-30 22:03:01
We want to relate $AF$ to parts of $ABC.$ Let's connect $F$ to the other two vertices:
We want to relate $AF$ to parts of $ABC.$ Let's connect $F$ to the other two vertices:
copeland
2012-03-30 22:03:06

copeland
2012-03-30 22:03:12
Too much. We want to focus on $AF$ and relating it to parts of $\triangle ABC.$ Let's finish out a couple of these triangles that use lengths we know we can get to.
Too much. We want to focus on $AF$ and relating it to parts of $\triangle ABC.$ Let's finish out a couple of these triangles that use lengths we know we can get to.
copeland
2012-03-30 22:03:18

copeland
2012-03-30 22:03:31
Now that's a little less terrifying.
Now that's a little less terrifying.
copeland
2012-03-30 22:03:40
We should be looking at $\triangle AFC$ and $\triangle AFB,$ hoping to relate them to other triangles in the diagram. I'd start with $\triangle AFC,$ since it spans less of the diagram and seems easier to focus on. What are we trying to find?
We should be looking at $\triangle AFC$ and $\triangle AFB,$ hoping to relate them to other triangles in the diagram. I'd start with $\triangle AFC,$ since it spans less of the diagram and seems easier to focus on. What are we trying to find?
copeland
2012-03-30 22:03:57
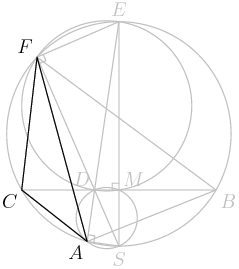

Xcellence
2012-03-30 22:04:17
AF
AF
brokenfixer
2012-03-30 22:04:17
eventually we want AF
eventually we want AF
ahaanomegas
2012-03-30 22:04:17
AF
AF
Duncanyang
2012-03-30 22:04:17
AF.
AF.
eccfcco15
2012-03-30 22:04:17
AF
AF
copeland
2012-03-30 22:04:23
Great.
Great.
copeland
2012-03-30 22:04:29
What will help us find that?
What will help us find that?
Fire-Sword
2012-03-30 22:05:28
arent triangles ABC and CFA similar?
arent triangles ABC and CFA similar?
brokenfixer
2012-03-30 22:05:28
a similar triangle and AC works
a similar triangle and AC works
copeland
2012-03-30 22:05:33
Perhaps $\triangle AFC$ and $\triangle CBA$ are similar. There are a few clues that this isn't the case. Most notably, that would lead us to an answer that doesn't fit the format of the problem. A less "cheating" way to check real quick that $AFC$ and $CBA$ aren't similar is to note that if $AFC$ and $CBA$ are similar, then they're congruent. A quick measurement with a compass or ruler would show that $AB$ and $FC$ aren't equal.
Perhaps $\triangle AFC$ and $\triangle CBA$ are similar. There are a few clues that this isn't the case. Most notably, that would lead us to an answer that doesn't fit the format of the problem. A less "cheating" way to check real quick that $AFC$ and $CBA$ aren't similar is to note that if $AFC$ and $CBA$ are similar, then they're congruent. A quick measurement with a compass or ruler would show that $AB$ and $FC$ aren't equal.
copeland
2012-03-30 22:06:06
However $\angle AFC = \angle ABC,$ since they're inscribed in the same arc. That's a really good start.
However $\angle AFC = \angle ABC,$ since they're inscribed in the same arc. That's a really good start.
copeland
2012-03-30 22:06:15
We do have $\angle AFC = \angle ABC,$ so we have something to look more closely at. Perhaps $\triangle AFC$ is similar to a triangle that includes $\angle ABC.$ There aren't many candidates! There are no notable points on $AB$ besides $A$ and $B,$ so we look at triangles with $AB$ as a side and the third vertex on $BC.$ The only candidates after dismissing $\triangle ABC$ are $\triangle ADB$ and $\triangle AMB.$
We do have $\angle AFC = \angle ABC,$ so we have something to look more closely at. Perhaps $\triangle AFC$ is similar to a triangle that includes $\angle ABC.$ There aren't many candidates! There are no notable points on $AB$ besides $A$ and $B,$ so we look at triangles with $AB$ as a side and the third vertex on $BC.$ The only candidates after dismissing $\triangle ABC$ are $\triangle ADB$ and $\triangle AMB.$
copeland
2012-03-30 22:06:23


copeland
2012-03-30 22:06:39
Which one looks like the better candidate?
Which one looks like the better candidate?
MathTwo
2012-03-30 22:07:20
AMB
AMB
brokenfixer
2012-03-30 22:07:20
AFC -> ABM
AFC -> ABM
Fire-Sword
2012-03-30 22:07:20
AMB
AMB
numbertheorist17
2012-03-30 22:07:20
AMB
AMB
ABCDE
2012-03-30 22:07:20
AMB
AMB
Duncanyang
2012-03-30 22:07:20
AMB
AMB
copeland
2012-03-30 22:07:24
$\angle AMB$ looks much more likely to be similar to $\angle AFC.$ (This is one example of why it's good to draw very precise diagrams!)
$\angle AMB$ looks much more likely to be similar to $\angle AFC.$ (This is one example of why it's good to draw very precise diagrams!)
copeland
2012-03-30 22:07:28
So, we'll go after $\angle AMB.$ We'd like to show that $\angle AMB = \angle ACF$ or $\angle MAB = \angle FAC.$ Which looks easier to chase with, $\angle AMB$ or $\angle MAB?$
So, we'll go after $\angle AMB.$ We'd like to show that $\angle AMB = \angle ACF$ or $\angle MAB = \angle FAC.$ Which looks easier to chase with, $\angle AMB$ or $\angle MAB?$
Duncanyang
2012-03-30 22:08:09
AMB
AMB
proglote
2012-03-30 22:08:09
AMB
AMB
numbertheorist17
2012-03-30 22:08:09
AMB
AMB
dantx5
2012-03-30 22:08:09
AMB
AMB
Xcellence
2012-03-30 22:08:09
AMB
AMB
math-rules
2012-03-30 22:08:11
AMB
AMB
copeland
2012-03-30 22:08:15
It looks easier to relate $\angle AMB$ to other parts of the diagram. It's hard to relate $\angle MAB$ to anything outside of $\triangle MAB$ (though it can be done-- think about extending $AM$ later).
It looks easier to relate $\angle AMB$ to other parts of the diagram. It's hard to relate $\angle MAB$ to anything outside of $\triangle MAB$ (though it can be done-- think about extending $AM$ later).
copeland
2012-03-30 22:08:24
What can we do with $\angle AMB?$
What can we do with $\angle AMB?$
copeland
2012-03-30 22:09:16
I bet I put that little circle in there for something. . . .
I bet I put that little circle in there for something. . . .
proglote
2012-03-30 22:10:04
it is 180 - CMA
it is 180 - CMA
brokenfixer
2012-03-30 22:10:04
look at supplemental AMD
look at supplemental AMD
copeland
2012-03-30 22:10:14
We have $\angle AMB = 180 - \angle DMA.$ What next?
We have $\angle AMB = 180 - \angle DMA.$ What next?
brokenfixer
2012-03-30 22:11:28
matches ASD
matches ASD
ABCDE
2012-03-30 22:11:28
angle DMA is equal to angle DSA
angle DMA is equal to angle DSA
Yongyi781
2012-03-30 22:11:28
AMB - 180 - AMD = 180 - ASD
AMB - 180 - AMD = 180 - ASD
sonchecky
2012-03-30 22:11:28
DMA = DSA
DMA = DSA
copeland
2012-03-30 22:11:33
Well, we have that surprising little circle there, and we haven't used it yet... Now looks like a good time.
Well, we have that surprising little circle there, and we haven't used it yet... Now looks like a good time.
copeland
2012-03-30 22:11:39


copeland
2012-03-30 22:11:46
We have $\angle AMB = 180 - \angle DMA = 180 - \angle DSA.$ What else can we do with $\angle DSA$?
We have $\angle AMB = 180 - \angle DMA = 180 - \angle DSA.$ What else can we do with $\angle DSA$?
Potla
2012-03-30 22:12:51
AMB=180-DMA=180-DSA=FCA
AMB=180-DMA=180-DSA=FCA
Potla
2012-03-30 22:12:51
DMA=DSA=180-FCA
DMA=DSA=180-FCA
admin25
2012-03-30 22:12:51
$ \angle DSA $ is the supplement to $ \angle ACF $, since $ ACFS $ is cyclic
$ \angle DSA $ is the supplement to $ \angle ACF $, since $ ACFS $ is cyclic
copeland
2012-03-30 22:12:59
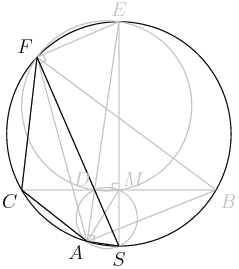

copeland
2012-03-30 22:13:03
From cyclic quad $FCAS,$ we have $\amgle AMB=180-\angle DSA = 180-\angle FSA = \angle FCA.$ SUCCESS!
From cyclic quad $FCAS,$ we have $\amgle AMB=180-\angle DSA = 180-\angle FSA = \angle FCA.$ SUCCESS!
copeland
2012-03-30 22:13:09
We now have $\angle AMB=\angle FCA$ and $\angle AFC = \angle ABM,$ so $\triangle AFC \sim\triangel ABM.$
We now have $\angle AMB=\angle FCA$ and $\angle AFC = \angle ABM,$ so $\triangle AFC \sim\triangel ABM.$
copeland
2012-03-30 22:13:12
gosh
gosh
copeland
2012-03-30 22:13:15
Let me try that again.
Let me try that again.
copeland
2012-03-30 22:13:23
From cyclic quad $FCAS,$ we have $\angle AMB=180-\angle DSA = 180-\angle FSA = \angle FCA.$ SUCCESS!
From cyclic quad $FCAS,$ we have $\angle AMB=180-\angle DSA = 180-\angle FSA = \angle FCA.$ SUCCESS!
copeland
2012-03-30 22:13:32
We now have $\angle AMB=\angle FCA$ and $\angle AFC = \angle ABM,$ so $\triangle AFC \sim\triangle ABM.$
We now have $\angle AMB=\angle FCA$ and $\angle AFC = \angle ABM,$ so $\triangle AFC \sim\triangle ABM.$
copeland
2012-03-30 22:13:39
What expression does that give us for $AF?$
What expression does that give us for $AF?$
Duncanyang
2012-03-30 22:14:49
AB/AF=AM/AC
AB/AF=AM/AC
brokenfixer
2012-03-30 22:14:49
AC / AF = AM / AB
AC / AF = AM / AB
sonchecky
2012-03-30 22:14:49
AF / AC = AB / AM, so AF = 2(AB)(AC)/(BC)
AF / AC = AB / AM, so AF = 2(AB)(AC)/(BC)
copeland
2012-03-30 22:14:53
We have $AF/AC = AB/AM,$ so $AF = AC\cdot AB/AM.$ Now we just have to find $AM.$
We have $AF/AC = AB/AM,$ so $AF = AC\cdot AB/AM.$ Now we just have to find $AM.$
copeland
2012-03-30 22:15:01
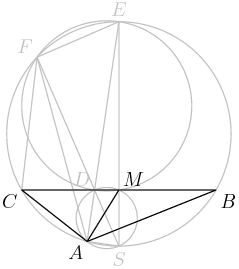

copeland
2012-03-30 22:15:07
Now we know $AC=3$, $AB=5$, and $CB=7$. There's a fancy theorem that tells us $AM$. The space in my brain is way too precious for me to place something as obscure as that in it, though.
Now we know $AC=3$, $AB=5$, and $CB=7$. There's a fancy theorem that tells us $AM$. The space in my brain is way too precious for me to place something as obscure as that in it, though.
copeland
2012-03-30 22:15:19
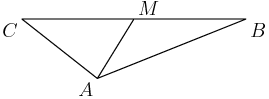

copeland
2012-03-30 22:15:27
Furthermore, there's a symmetry argument that will tell us $M$ quickly what should we draw?
Furthermore, there's a symmetry argument that will tell us $M$ quickly what should we draw?
ABCDE
2012-03-30 22:16:12
parallelogram?
parallelogram?
Fire-Sword
2012-03-30 22:16:12
another triangle with identical lines on the other side sharing side CB?
another triangle with identical lines on the other side sharing side CB?
brokenfixer
2012-03-30 22:16:12
A' reflecting A over ES
A' reflecting A over ES
heliootrope
2012-03-30 22:16:12
a parallelogram!
a parallelogram!
copeland
2012-03-30 22:16:16
$M$ is the midpoint. We can rotate the entire triangle by an angle of $180^\circ$ around $M$:
$M$ is the midpoint. We can rotate the entire triangle by an angle of $180^\circ$ around $M$:
copeland
2012-03-30 22:16:22

copeland
2012-03-30 22:16:34
$AM$ is half the diagonal of this parallelogram. The sum of the squares of the diagonals is the sum of the squares of the (four) side lengths. (Try proving that on your own! There are several pretty quick proofs.) What is $AM^2$?
$AM$ is half the diagonal of this parallelogram. The sum of the squares of the diagonals is the sum of the squares of the (four) side lengths. (Try proving that on your own! There are several pretty quick proofs.) What is $AM^2$?
copeland
2012-03-30 22:17:18
AC=3, AB=5, BC=7.
AC=3, AB=5, BC=7.
brokenfixer
2012-03-30 22:18:31
3^2+5^2+3^2+5^2 = 68 = 49+ 4*AM^2
3^2+5^2+3^2+5^2 = 68 = 49+ 4*AM^2
Duncanyang
2012-03-30 22:18:31
2(34)=49^2+(2AM)^2
2(34)=49^2+(2AM)^2
nackster12
2012-03-30 22:18:31
19/2
19/2
sonchecky
2012-03-30 22:18:31
$AM^2 = 1/4 (AA')^2 = 1/4 (3^2 + 3^2 + 5^2 + 5^2 - 7^2) = 19/4$
$AM^2 = 1/4 (AA')^2 = 1/4 (3^2 + 3^2 + 5^2 + 5^2 - 7^2) = 19/4$
brokenfixer
2012-03-30 22:18:31
19/4
19/4
Potla
2012-03-30 22:18:37
19/4
19/4
copeland
2012-03-30 22:19:24
$AM^2=\frac{(AA')^2}4=\frac{2AC^2+2AB^2-CB^2}4=\frac{18+50-49}{4}=\frac{19}4$.
$AM^2=\frac{(AA')^2}4=\frac{2AC^2+2AB^2-CB^2}4=\frac{18+50-49}{4}=\frac{19}4$.
copeland
2012-03-30 22:19:27
And what is $AF^2?$
And what is $AF^2?$
Potla
2012-03-30 22:20:12
900/19
900/19
numbertheorist17
2012-03-30 22:20:12
900/19
900/19
sonchecky
2012-03-30 22:20:12
$AF^2 = (AB)^2 (AC)^2 / (AM)^2 = \frac{3^2 (5^2)}{19/4} = \frac{900}{19}$
$AF^2 = (AB)^2 (AC)^2 / (AM)^2 = \frac{3^2 (5^2)}{19/4} = \frac{900}{19}$
brokenfixer
2012-03-30 22:20:12
3^2 5^2 * (4/19)
3^2 5^2 * (4/19)
heliootrope
2012-03-30 22:20:12
900/19
900/19
numbertheorist17
2012-03-30 22:20:12
900/19, So 919
900/19, So 919
copeland
2012-03-30 22:20:38
$AF^2 = \frac{AC^2\cdot AB^2}{AM^2}=\frac{3^2\cdot5^2}{\frac{19}4}=\frac{3^2\cdot10^2}{19}=\frac{900}{19}.$
$AF^2 = \frac{AC^2\cdot AB^2}{AM^2}=\frac{3^2\cdot5^2}{\frac{19}4}=\frac{3^2\cdot10^2}{19}=\frac{900}{19}.$
copeland
2012-03-30 22:20:43
These integers are relatively prime, so the answer is $\boxed{919}$.
These integers are relatively prime, so the answer is $\boxed{919}$.
copeland
2012-03-30 22:20:48
Woohoo!
Woohoo!
copeland
2012-03-30 22:20:49
We win.
We win.
ahaanomegas
2012-03-30 22:21:08
That was spectular!
That was spectular!
brokenfixer
2012-03-30 22:21:08
hooray
hooray
alex31415
2012-03-30 22:21:08
Wow! That Math Jam was probably the longest one in history!
Wow! That Math Jam was probably the longest one in history!
copeland
2012-03-30 22:21:11
Yeah, that's what I was thinking.
Yeah, that's what I was thinking.
copeland
2012-03-30 22:21:19
That's what we get for having me do the AIME. :)
That's what we get for having me do the AIME. :)
ahaanomegas
2012-03-30 22:21:25
That was spectacular!
That was spectacular!
19oshawott98
2012-03-30 22:21:25
WE win PUDDING!!!!
WE win PUDDING!!!!
ahaanomegas
2012-03-30 22:21:25
What a problem!
What a problem!
-Transcend-
2012-03-30 22:21:25
wow, that was an intense geometry problem
wow, that was an intense geometry problem
Fire-Sword
2012-03-30 22:21:25
pudding time!
pudding time!
Potla
2012-03-30 22:21:25
Great
Great
copeland
2012-03-30 22:21:42
OK, now it's time for me to sleep.
OK, now it's time for me to sleep.
copeland
2012-03-30 22:21:55
Thanks, everyone, for sticking around. It's been rad.
Thanks, everyone, for sticking around. It's been rad.
sonchecky
2012-03-30 22:22:00
This was even longer than the actual AIME, but thank you for your time doing this!
This was even longer than the actual AIME, but thank you for your time doing this!
math-rules
2012-03-30 22:22:00
ok. goodnight
ok. goodnight
alex31415
2012-03-30 22:22:00
Good night!
Good night!
Potla
2012-03-30 22:22:10
Good night
Good night
ahaanomegas
2012-03-30 22:22:10
Good night!
Good night!
proglote
2012-03-30 22:22:10
bye :)
bye :)
math-rules
2012-03-30 22:23:04
Good night
Good night
eccfcco15
2012-03-30 22:23:04
Thanks, and good night
Thanks, and good night
ahaanomegas
2012-03-30 22:23:04
Thanks a lot, Mr. Copeland, and, of course, the TAs such as Aryth and Mr. Lian!
Thanks a lot, Mr. Copeland, and, of course, the TAs such as Aryth and Mr. Lian!
copeland
2012-03-30 22:23:58
Alright, I'm going to shut down the room now. Thanks everyone!
Alright, I'm going to shut down the room now. Thanks everyone!
copeland
2012-03-30 22:25:24
Once I figure out how.
Once I figure out how.
copeland
2012-03-30 22:26:50
OK, I can't purge the room.
OK, I can't purge the room.
copeland
2012-03-30 22:26:56
But you should go now.
But you should go now.
copeland
2012-03-30 22:26:59
Really.
Really.
copeland
2012-03-30 22:27:02
The show's over.
The show's over.
copeland
2012-03-30 22:27:03
Thanks a lot.
Thanks a lot.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









