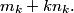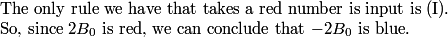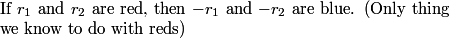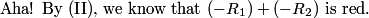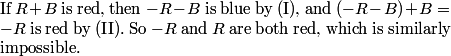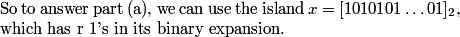Math Jams

rrusczyk 2012-06-26 19:00:40
Greetings and welcome to our Math Jam! Tonight, Yasha Berchenko-Kogan will host a discussion of the Qualifying Quiz for Canada/USA Mathcamp.

rrusczyk 2012-06-26 19:01:04
I first met Yasha many years ago. Guess where?

Mathpather 2012-06-26 19:01:19
mathcamp

yingted 2012-06-26 19:01:19
Mathcamp!

rrusczyk 2012-06-26 19:01:23
That's right!

rrusczyk 2012-06-26 19:01:46
I would later have dinner with him at the State Department, when he was a USAMO winner.

rrusczyk 2012-06-26 19:02:02
Now, we're very happy to have him as an instructor here at AoPS.

rrusczyk 2012-06-26 19:02:28
For those of you new to our classroom, the room is moderated, which means that everything you type will go to the instructors, not straight into the room.

rrusczyk 2012-06-26 19:02:38
Now, I'll turn the room over to Yasha!

Yasha 2012-06-26 19:02:55
Thanks Richard!

Yasha 2012-06-26 19:03:08
Hello everyone! Welcome to the Math Jam for the 2012 Mathcamp Qualifying Quiz.

Yasha 2012-06-26 19:03:31
My name is Yasha. I am a former student and counselor at Mathcamp, and I helped grade this year's quiz. As Richard mentioned, I'm also an instructor here at AoPS.

Yasha 2012-06-26 19:03:34
I'll be visiting camp in week 4 this summer, so I'll see some of you there.

Yasha 2012-06-26 19:03:50
For those of you who aren't familiar with it, the Mathcamp Qualifying Quiz is a seven-question untimed set of problems which all applicants to Canada/USA Mathcamp must solve for admission. You don't need to solve all of the problems, but you need to make good progress! It's one of several factors that impacts your admission. I'm expecting that many of you were indeed applicants this year. To follow along, you should all have the quiz open in another window: http://www.mathcamp.org/prospectiveapplicants/quiz/index.php

Yasha 2012-06-26 19:04:03
Additionally, if you did apply this year, I recommend having your solutions open. That way, you can reply more quickly to the questions I ask of the room. I like to have a very interactive session, so I'm expecting you all to pitch in to the solutions!

Yasha 2012-06-26 19:04:15
Also, feel free to ask questions at any time.

Yasha 2012-06-26 19:04:24
We are going to go through all seven problems on the quiz. I'm going to try to show you more than just fully correct answers: I also want to show you how you could come up with those answers, and how to write them up in a way that really communicates the mathematics you're doing.

Yasha 2012-06-26 19:04:35
This whole session is rather experimental --- we've only done it once before --- so I'd love to get your comments during or after the session on how it went and how useful it was (or wasn't).

Yasha 2012-06-26 19:04:44
We're going to start relatively slowly, but accelerate as we go along. The idea is for everyone to be able to follow at first, but be warned that things will get more and more difficult as we go on.

Yasha 2012-06-26 19:05:22
As Richard mentioned, this chat room is moderated. That means your messages go only to me, and I will choose which to pass on, so feel free to contribute to problems and ask questions.

Yasha 2012-06-26 19:05:46
If you have any questions about how we select problems or how we grade solutions, save them and I'll try to leave time to answer them at the end of the Math Jam. If I don't end up getting to them, feel free to post them on the Mathcamp forum on AoPS at http://www.artofproblemsolving.com/Forum/viewforum.php?f=314

Yasha 2012-06-26 19:06:20
For now, let's go ahead and tackle these problems!

Yasha 2012-06-26 19:06:24
Problem 1: Frog Catching.

Yasha 2012-06-26 19:06:29

Watermelon876 2012-06-26 19:06:42
The problems have names?

Yasha 2012-06-26 19:06:46
They do now!

Yasha 2012-06-26 19:06:54

Yasha 2012-06-26 19:07:07
First off, there's some ambiguity in the wording of the problem: When you make your first guess, it's not clear whether the problem intends for the frog to have had time for one jump or two. We accepted solutions based on either interpretation, but for the sake of staying on the same page in this Math Jam, let's interpret the problem to mean that the frog had time for one jump when you make your first guess. So, for example, if n=17, then when you make your first guess the frog is at 17, when you make your second guess the frog is at 34, and so forth.

Yasha 2012-06-26 19:07:28
So, how can we catch the frog without knowing what n is?

Watermelon876 2012-06-26 19:07:50
we can guess a value of n equal ot the elapsed seconds.

viperstrike 2012-06-26 19:07:55
after the first second the frog is on n and we begin guessing its location. so after s seconds the frog is on the integer x=ns

CDerwin1 2012-06-26 19:08:00
we can systematically check each n

Yasha 2012-06-26 19:08:14
We can systematically go through all the possibilities for n, starting with n=1, then n=2, then n=3, and so forth. Each time we guess a value for n, we search the integer where we'd expect the frog to be if our guess were correct. Eventually, we'll guess the right value and find the frog.

Yasha 2012-06-26 19:08:24
For our first guess, we guess that n=1. Where should we search for the frog?

jared429 2012-06-26 19:08:40
1

dantx5 2012-06-26 19:08:40
at 1

numbertheorist17 2012-06-26 19:08:40
at 1

Watermelon876 2012-06-26 19:08:40
n*s=1*1=1

viperstrike 2012-06-26 19:08:40
1

Yasha 2012-06-26 19:08:47
The frog has had time to jump once, so, assuming n=1, it will be at the integer 1. We should search there. If we don't find it, we guess that n=2. Where should we search for the frog for our second guess?

theGoodGuy 2012-06-26 19:08:58
4

yingted 2012-06-26 19:08:58
4

numbertheorist17 2012-06-26 19:08:58
at 4

nemarci 2012-06-26 19:09:07
4

dantx5 2012-06-26 19:09:08
4

jjchoi5 2012-06-26 19:09:08
4

MA7HL0V3R 2012-06-26 19:09:08
4

spacebacon99 2012-06-26 19:09:08
4

viperstrike 2012-06-26 19:09:08
4

Yasha 2012-06-26 19:09:14
By the time we make our second guess, the frog has had time to jump twice. Assuming n=2, the frog jumped 2 to the right each time, so it will end up at the integer 4. We search there. Where do we search for our third guess?

yingted 2012-06-26 19:09:31
9

theGoodGuy 2012-06-26 19:09:31
9

CDerwin1 2012-06-26 19:09:31
9

dantx5 2012-06-26 19:09:31
9

numbertheorist17 2012-06-26 19:09:31
9

frtennis1 2012-06-26 19:09:31
9

nemarci 2012-06-26 19:09:31
9

spacebacon99 2012-06-26 19:09:31
6

jjchoi5 2012-06-26 19:09:31
9

numbertheorist17 2012-06-26 19:09:31
9

Watermelon876 2012-06-26 19:09:31

Mathpather 2012-06-26 19:09:31
3^2=9

MA7HL0V3R 2012-06-26 19:09:31
9

Yasha 2012-06-26 19:09:39
For our third guess, we guess that n=3. Since the frog has had time to jump three times, it will be at the integer 9, so we search there.

dantx5 2012-06-26 19:09:54
perfect square integers?

melikababadi 2012-06-26 19:09:54
n^2?

Mathpather 2012-06-26 19:09:54
so we check n^2 for the frog at each n

numbertheorist17 2012-06-26 19:09:54
basically at every perfect square

viperstrike 2012-06-26 19:09:54
since n=s x is a perfect sqaure

Yasha 2012-06-26 19:10:12
On our kth guess, we guess that n=k. By then, the frog has had time to jump k times going k to the right each time, landing on the integer k^2.

19oshawott98 2012-06-26 19:11:02
but what about the second in the beginning

Yasha 2012-06-26 19:11:05
The problem is a bit ambiguous about whether the frog got to jump once or twice when you make your first guess. We accepted both interpretations, but for the MathJam we're sticking with once.

Yasha 2012-06-26 19:11:23
OK, so our strategy is to search the integer k^2 on guess number k. How long will it take us to catch the frog?

frtennis1 2012-06-26 19:11:42
n times

Mathpather 2012-06-26 19:11:42
n seconds

koel17 2012-06-26 19:11:45
n seconds

Yasha 2012-06-26 19:11:52
We will catch the frog on guess number n. On that guess, we will search integer n^2, which is where the frog will be after n seconds.

Yasha 2012-06-26 19:11:59
Any questions about this part?

Yasha 2012-06-26 19:12:16

Yasha 2012-06-26 19:12:27
How can we modify our reasoning in part (a) to solve this problem?

Yasha 2012-06-26 19:12:48
In part (b), we need to not only go through all of the possibilities for n, but also both possibilities for the frog's direction.

Yasha 2012-06-26 19:12:53
How can we take into account all of the possibilities in our search for the frog?

Mathpather 2012-06-26 19:13:06
we check n=1, n=-1, n=2, n=-2, and so on

spacebacon99 2012-06-26 19:13:06
we first try a positive n, and then a negative n

Watermelon876 2012-06-26 19:13:06
alternate between positive and negative guesses (starting with 0)

CDerwin1 2012-06-26 19:13:06
we can check n=1,n=-1,n=2,n=-2,etc.

yingted 2012-06-26 19:13:06
alternate positive and negative numbers

dantx5 2012-06-26 19:13:06
find if the frog's jumps are -1, then 1, then -2, then 2, and so on

Yasha 2012-06-26 19:13:15
Here's one way to do it: On our first guess, we assume that n=1 and the frog goes right. On the second guess, we assume n=1 and left, on the third guess, we assume n=2 and right, on the fourth guess, we assume n=2 and left, and so forth.

Yasha 2012-06-26 19:13:21
To make matters easier, we can use negative values of n to denote motion to the left, and positive values to denote motion to the right. For example, n=-3 means the frog jumps three units to the left each second, and n=5 means the frog jumps five units to the right each second.

Yasha 2012-06-26 19:13:31
The order we have for guessing the values of n is 1, -1, 2, -2, 3, -3, and so forth.

Yasha 2012-06-26 19:13:38
Of course, a different order can work just as well, such as -1, 1, -2, 2, -3, 3, and so forth.

Yasha 2012-06-26 19:13:49
The important part is that every possibility for the frog's jumping strength and direction appears in this list, so, eventually, we will guess the correct value of n.

Yasha 2012-06-26 19:13:59
OK, so assuming that the order in which we guess the values of n is 1, -1, 2, -2, 3, -3, etc., what should be the first integer we search?

Mathpather 2012-06-26 19:14:12
1

dantx5 2012-06-26 19:14:12
1

MA7HL0V3R 2012-06-26 19:14:12
1

yingted 2012-06-26 19:14:12
1

viperstrike 2012-06-26 19:14:12
1

spacebacon99 2012-06-26 19:14:12
1

frtennis1 2012-06-26 19:14:12
1

Yasha 2012-06-26 19:14:20
If n=1, then after one second the frog will be at the integer 1, so we should search there. What about the second integer we search?

Mathpather 2012-06-26 19:14:30
-2

Watermelon876 2012-06-26 19:14:30
-2

yingted 2012-06-26 19:14:30
-2

jared429 2012-06-26 19:14:30
-2

dantx5 2012-06-26 19:14:30
-2

frtennis1 2012-06-26 19:14:30
-2

nemarci 2012-06-26 19:14:30
-2

CDerwin1 2012-06-26 19:14:30
-2

numbertheorist17 2012-06-26 19:14:30
-2

MA7HL0V3R 2012-06-26 19:14:30
-2

spacebacon99 2012-06-26 19:14:30
-2

esque 2012-06-26 19:14:30
-2

Yasha 2012-06-26 19:14:36
On our second guess, we decided to check the possibility that n=-1. If n=-1, then after two seconds the frog will be at the integer -2, so we search there. What about the third guess?

nemarci 2012-06-26 19:15:00
6

Mathpather 2012-06-26 19:15:00
6

viperstrike 2012-06-26 19:15:00
then 6

dantx5 2012-06-26 19:15:00
6

MA7HL0V3R 2012-06-26 19:15:00
6

Watermelon876 2012-06-26 19:15:00
6

melikababadi 2012-06-26 19:15:00
6

yingted 2012-06-26 19:15:00
6

viperstrike 2012-06-26 19:15:00
6

Yasha 2012-06-26 19:15:08
On our third guess, we decided to assume that n=2. If n=2, then after three seconds the frog will be at the integer 6.

Yasha 2012-06-26 19:15:17
Likewise, on our fourth guess, we assume that n=-2. Then, after four seconds, the frog will be at the integer -8.

Yasha 2012-06-26 19:15:22
We now have a strategy for catching the frog: On our kth guess, we look at the kth term of the sequence 1, -1, 2, -2, 3, -3, .... This term gives us the value of n that we'd like to test. We multiply it by k (the number of seconds since the frog started) to find where the frog would be if our guess for n were correct, and we search at that integer.

jwp 2012-06-26 19:16:14
but how do we know the pace of the frog?

Yasha 2012-06-26 19:16:16
We don't, that's the beauty of it. We make a guess for the pace of the frog each time we search. Since we guess systematically, eventually we will be right.

Yasha 2012-06-26 19:16:35
At some point, we will reach n in the sequence, and at that point we will search for the frog in the correct place and catch it.

marupiravi 2012-06-26 19:16:59
how will we know we are right

Yasha 2012-06-26 19:17:00
We'll know because there will be a frog at the integer we search, and then we stop.

Yasha 2012-06-26 19:17:26
We have a strategy for catching the frog, so we've done everything the problem asked for, but let's go ahead and see if we can find an actual formula for the integer we should search on guess number k.

Yasha 2012-06-26 19:17:38
How can we start?

Watermelon876 2012-06-26 19:18:13
Write the sequence 1,-1,2,-2... in terms of t

Mathpather 2012-06-26 19:18:13
n odd and n even are different

theGoodGuy 2012-06-26 19:18:13
+- floor(k/2)*n

Yasha 2012-06-26 19:18:34
We consider the cases where k is odd and even separately, because on odd guesses we guess positive values of n, and on even guesses we guess negative values of n.

Yasha 2012-06-26 19:18:39
Let's first work with the case where k is odd. What is the value of n that we test on guess number k, in terms of k?

Yasha 2012-06-26 19:19:05
The value of n that we'd like to test is the kth term of the sequence 1, -1, 2, -2, 3, -3, .... What is the kth term of this sequence, in terms of k?

Yasha 2012-06-26 19:19:18
(We're working with odd k for now.)

yingted 2012-06-26 19:19:31
(k+1)/2

Yasha 2012-06-26 19:19:37

Yasha 2012-06-26 19:19:42
You can check the first couple of values to make sure that you're not off by one: When k=1 our guess is n=1. When k=3 our guess is n=2, and so forth.

Yasha 2012-06-26 19:19:58
At what integer should we search for the frog on our kth guess, where k is odd?

Watermelon876 2012-06-26 19:20:24

Mathpather 2012-06-26 19:20:24
k(k+1)/2

esque 2012-06-26 19:20:24
k(k+1)/2

Watermelon876 2012-06-26 19:20:24

Yasha 2012-06-26 19:20:29

Yasha 2012-06-26 19:20:36
OK, let's move on to even values of k. What value of n do we test on our kth guess when k is even?

yingted 2012-06-26 19:20:54
-k/2

MA7HL0V3R 2012-06-26 19:20:54
-k/2

Yasha 2012-06-26 19:21:00

Yasha 2012-06-26 19:21:07
At what integer should we search for the frog?

Mathpather 2012-06-26 19:21:24
-(k^2)/2

yingted 2012-06-26 19:21:24
-k^2/2

nemarci 2012-06-26 19:21:24
-k^2/2

Yasha 2012-06-26 19:21:40

Yasha 2012-06-26 19:21:51

frtennis1 2012-06-26 19:22:55
Around n*2 tries

Watermelon876 2012-06-26 19:22:55
If n is positive, 2n-1. If n is neg. -2n

dantx5 2012-06-26 19:22:55
2n-1 odd, 2n even

Yasha 2012-06-26 19:23:04

Yasha 2012-06-26 19:23:22

Yasha 2012-06-26 19:23:33
Any questions on this part?

Yasha 2012-06-26 19:23:49

Yasha 2012-06-26 19:24:07
Like in the previous part, let's let negative values of n denote moving to the left, and positive values of n denote moving to the right.

Yasha 2012-06-26 19:24:17
Also, let's let the variable m represent the frog's starting point.

Yasha 2012-06-26 19:24:24
What would we need to do in order to be able to use a strategy similar to the one we've used in the previous parts?

skycao 2012-06-26 19:24:40
count all the lattice points

Maz906 2012-06-26 19:24:52
check where the frog is for various (m,n)

frtennis1 2012-06-26 19:24:52
Find a way to systematically navigate all possible combinations of n and m

Watermelon876 2012-06-26 19:24:52
We need a way to biject pairs of m and n to the natural numbers (time in seconds)

yingted 2012-06-26 19:24:52
search the half-plane (m,n),n>0

Yasha 2012-06-26 19:24:58
We'd need to go through all possible pairs (n,m), testing one of them each guess.

Yasha 2012-06-26 19:25:04
Each guess, we'd search the integer where we'd expect the frog to be if our guess (n,m) of its jumping speed and initial position were correct. We want to eventually hit every possibility for (n,m). If we manage that, then at some point our guess (n,m) will be correct, and we'll find the frog.

Yasha 2012-06-26 19:25:25
So, how can we go through all of the possibilities for (n,m)?

Yasha 2012-06-26 19:25:55
Unfortunately, we can't let n=1 and go through all possibilities for m, and then move to n=-1, then n=2, and so forth: Since there are infinitely many values of m to try, we'll never actually get to n=-1!

Watermelon876 2012-06-26 19:26:43
We can draw a spiral on the np-plane where p is the initial position

Mathpather 2012-06-26 19:26:43
we spiral out from the origin of a cartesian plane

skycao 2012-06-26 19:26:43
spiral

frtennis1 2012-06-26 19:26:43
Try a spiral in the coordinate plane of n and m

Watermelon876 2012-06-26 19:26:43
You can do this by drawing a spiral starting from 0,0 to 0,1 to 1,1 to 0,1 to -1,1, to -1,0...

yingted 2012-06-26 19:26:43
for all m: for all n from 0 to m: try (n,m-n)

Yasha 2012-06-26 19:27:26
There are a lot of possible solutions, and all of them involve first taking those (n,m) where both n and m are small, and then gradually increasing them.

Yasha 2012-06-26 19:27:56
A lot of these ways look like spiraling out from the origin.

Yasha 2012-06-26 19:28:06
Here's one way to do it explicitly:

Yasha 2012-06-26 19:28:11
First, guess all possibilities for n and m where both of their absolute values are less than or equal to one. There are finitely many of these:

Yasha 2012-06-26 19:28:16

Yasha 2012-06-26 19:28:31
Next, guess all possibilities for n and m where both of their absolute values are less than or equal to two, (ignoring the ones we have guessed already). There are also finitely many of these:

Yasha 2012-06-26 19:28:40

Yasha 2012-06-26 19:28:50
Next, we continue up to three:

Yasha 2012-06-26 19:28:55

Yasha 2012-06-26 19:29:00

Yasha 2012-06-26 19:29:13
We can continue this way indefinitely, and we will eventually list every possible pair (n,m).

bobthesmartypants 2012-06-26 19:29:21
like with concentric circles?

Yasha 2012-06-26 19:29:29
Yup, sort of.

Yasha 2012-06-26 19:29:34
If you want to visualize this process geometrically, consider the pairs (n,m) as locations in the plane. We first take all the pairs (n,m) in a small square around the origin. Then we increase the size of the square, and we take all of the new pairs (n,m) that are now inside of it. Then we increase the size of the square again, and so forth.

viperstrike 2012-06-26 19:30:07
what is n and m

Yasha 2012-06-26 19:30:09
n was the velocity of the frog, and m was its starting location.

marupiravi 2012-06-26 19:30:39
all we have to do is make m zero and then move up on the value of n

Yasha 2012-06-26 19:30:41
If you do that, you'll only test the possibilities where m=0. You'll never get to any other values of m.

frtennis1 2012-06-26 19:30:53
Can this be put into an explict formula though?

Yasha 2012-06-26 19:31:11
You could, but it would be a very messy formula.

yingted 2012-06-26 19:31:16
using sqrt and floor :(

marupiravi 2012-06-26 19:31:39
you say n was so does that mean that the velocity of the frog has changed

Yasha 2012-06-26 19:31:43
No, the velocity of the frog stays the same, but our guess for the velocity of the frog changes.

Yasha 2012-06-26 19:32:58
Like I mentioned while we were doing part (b), the problem just asks for a strategy, which may or may not involve a formula.

Yasha 2012-06-26 19:33:15
We came up with a formula in (b) because it was easy, but I won't do it for (c), though it is possible.

Yasha 2012-06-26 19:33:38
In any case, we now have an infinite list of pairs (n,m).

Yasha 2012-06-26 19:33:46

yingted 2012-06-26 19:34:12
m_k+kn_k

nemarci 2012-06-26 19:34:25
m_k+k*n_k

Watermelon876 2012-06-26 19:34:25

Yasha 2012-06-26 19:34:28

Yasha 2012-06-26 19:34:39

Yasha 2012-06-26 19:35:52
You wouldn't need an explicit formula to get full credit. However, writing an explicit formula is a good way to make sure that your solution is a complete strategy.

Yasha 2012-06-26 19:36:11
Sorry, that was in response to the question:

Setalia 2012-06-26 19:36:13
So, for parts (a) and (b), did we get more "credit" or were our solutions given more weight if we had an explicit formula for which spot to search and how long it would take?

spacebacon99 2012-06-26 19:36:55
so in the test, you write this whole explanation down?

Yasha 2012-06-26 19:36:58
You'd want to write enough to have a complete argument. I've included more details and examples than is necessary for a complete solution.

viperstrike 2012-06-26 19:37:15
how long will this take

Yasha 2012-06-26 19:37:33
I'm aiming for two hours, but we'll see. If you get tired you don't have to stay of course.

Yasha 2012-06-26 19:37:57
Or perhaps you were talking about catching the frog.

Yasha 2012-06-26 19:38:13
You can work it out afterwards if you'd like.

marupiravi 2012-06-26 19:38:16
yingted said m_k+kn_k what does mean (undrescore)

Yasha 2012-06-26 19:38:21
The underscore means subscript.

Yasha 2012-06-26 19:38:34

Yasha 2012-06-26 19:38:40
We'll discuss all seven.

upleit 2012-06-26 19:38:42
How many questions are we going to discuss?

Yasha 2012-06-26 19:38:51
Anyways, let's move on.

Yasha 2012-06-26 19:38:55
Problem 2: Coloring the number line.

Yasha 2012-06-26 19:38:58
Each integer on the number line is colored with exactly one of three possible colors—red, green or blue—according to the following two rules: the negative of a red number must be colored blue, and the sum of two blue numbers (not necessarily distinct) must be colored red.

Yasha 2012-06-26 19:39:03
(a) Show that the negative of a blue number must be colored red and the sum of two red numbers must be colored blue.

Yasha 2012-06-26 19:39:20
Okay, so we have two rules that we know the coloring must satisfy. Let's give them names so that we can cite them in our argument.

Yasha 2012-06-26 19:39:24
(I) The negative of a red number is blue.
(II) The sum of two blue numbers is red.

Yasha 2012-06-26 19:39:34
Let's start by showing that the negative of a blue number must be red. Where do we start?

Yasha 2012-06-26 19:39:51

esque 2012-06-26 19:40:16
-B_0 is red

AwesomeToad 2012-06-26 19:40:16

jared429 2012-06-26 19:40:16

Watermelon876 2012-06-26 19:40:16
-b is red

Mathpather 2012-06-26 19:40:16
-B_0 is red

Maz906 2012-06-26 19:40:16
-B_0 is red

koel17 2012-06-26 19:40:16
-B_0 is red

spacebacon99 2012-06-26 19:40:16
-B_0 is red

Yasha 2012-06-26 19:40:22

bobthesmartypants 2012-06-26 19:40:39
by following the rules?

yingted 2012-06-26 19:40:56
2b is red

Yasha 2012-06-26 19:41:10

Yasha 2012-06-26 19:41:14
Now what?

yingted 2012-06-26 19:41:28
-2b is blue

Maz906 2012-06-26 19:41:28
by (II) 2B_0 is red, by (I) -2B_0 is blue

Watermelon876 2012-06-26 19:41:28
That means that -2b is blue

Yasha 2012-06-26 19:41:32

Watermelon876 2012-06-26 19:42:10
-b=-2b+b. We're done as those are both blue and sum to a red

esque 2012-06-26 19:42:10
by rule 2, -2b+b = -b must be red and we win

Tonitruant 2012-06-26 19:42:10
-2b+b=-b is red.

Yasha 2012-06-26 19:42:18

Yasha 2012-06-26 19:42:23

spacebacon99 2012-06-26 19:43:42
a red number is x. a blue number will be -x. if x is already negative, then the colors are switched...?

Yasha 2012-06-26 19:43:46
Nope, so before proving this, we might have thought that 10 is blue and -10 is green. Now we know that that's impossible.

Yasha 2012-06-26 19:44:11
Now let's show that the sum of two red numbers must be blue. How do we start?

Watermelon876 2012-06-26 19:44:15

Yasha 2012-06-26 19:44:23

Yasha 2012-06-26 19:44:38

nemarci 2012-06-26 19:44:56
-r_1-r_2 is red

viperstrike 2012-06-26 19:45:02
thus -(n1+n2) is red and negating this sum n1+N2 IS BLUE

Maz906 2012-06-26 19:45:04
then -R_1 + (-R_2) is the sum of two blue numbers, which must be red by (II)

Yasha 2012-06-26 19:45:14

Yasha 2012-06-26 19:45:20

spacebacon99 2012-06-26 19:46:07
what's the point of the green color?

Yasha 2012-06-26 19:46:10
If it weren't for the green color, we could say that something that isn't red must be blue. But with the green color there, we don't know that.

Yasha 2012-06-26 19:46:19
Okay, that wasn't too hard. But that part of the problem was just the warm-up!

Yasha 2012-06-26 19:46:24
(b) Determine all possible colorings of the integers that satisfy these rules.

Yasha 2012-06-26 19:46:41
First, let's restate our rules, now including the two new ones we've just proved.

Yasha 2012-06-26 19:46:46
(I) The negative of a red number is blue, and the negative of a blue number is red.
(II) The sum of two red numbers is blue, and the sum of two blue numbers is red.

Yasha 2012-06-26 19:47:03
Just looking at these rules, do you notice anything important?

yingted 2012-06-26 19:47:22
symmetry!

Maz906 2012-06-26 19:47:22
no mention of green numbers

Yasha 2012-06-26 19:47:31
Right. There is symmetry between red and blue numbers in the following sense: if you exchanged the words "red" and "blue" in the above rules, you would get the same set of rules.

Yasha 2012-06-26 19:47:37
That implies that if we have any coloring that fits these rules, we can swap the red and blue numbers, and get another legal coloring! That kind of observation will definitely save us some work.

Yasha 2012-06-26 19:47:52
Also, there is no mention of green in the rules.

Yasha 2012-06-26 19:48:03
Can you think of any colorings that fit these rules?

viperstrike 2012-06-26 19:48:20
all greens

skycao 2012-06-26 19:48:20
all numbers are green

yingted 2012-06-26 19:48:20
all green :(

CDerwin1 2012-06-26 19:48:20
everything green

Yasha 2012-06-26 19:48:26
Of course. The rules don't place any restrictions on green numbers, so we could color all the integers green! Do you think that's the only possibility?

viperstrike 2012-06-26 19:48:37
no

yingted 2012-06-26 19:48:38
no

dantx5 2012-06-26 19:48:38
no

Yasha 2012-06-26 19:48:43
Let's start with assuming there's at least one non-green integer, and see where we get. Suppose, say, 0 is blue.

bobthesmartypants 2012-06-26 19:49:10
then that doesn't work

Tonitruant 2012-06-26 19:49:10
-0 must be red?

Maz906 2012-06-26 19:49:10
then it's also red, since -0 = 0 must be red

Watermelon876 2012-06-26 19:49:10
then 0 is red because -0=0

nemarci 2012-06-26 19:49:10
then 0 has to be red, because 0=-0

bobthesmartypants 2012-06-26 19:49:10
cause then -0 = 0 must be red

Yasha 2012-06-26 19:49:16
Uh-oh. 0 can't be blue, because then -0 is red.

Yasha 2012-06-26 19:49:21
Obviously, 0 can't be red either, because then -0 would be blue. Therefore, 0 is green. Okay, one integer down.

Yasha 2012-06-26 19:49:27
Let's start by assuming 1 is blue, then. Then 2 is red. What about 3?

Yasha 2012-06-26 19:49:40
We don't have a rule for the sum of a red and blue number. Could 3 be blue?

yingted 2012-06-26 19:49:57
-1+3=2

nemarci 2012-06-26 19:50:01
no

Yasha 2012-06-26 19:50:06
No, because then -3 is red, and -3 + 2 = -1 must be blue, which makes 1 red.

marupiravi 2012-06-26 19:50:40
negative zero does not exict

Yasha 2012-06-26 19:50:41
No, it's fine. -0 is equal to 0.

Yasha 2012-06-26 19:50:51
Could 3 be red?

yingted 2012-06-26 19:51:00
no

yingted 2012-06-26 19:51:10
-1+3=2, -2+3=1

Yasha 2012-06-26 19:51:18
No, because then -3 is blue, and -3 + 1 = -2 is red, which makes 2 blue. So 3 must be green.

dantx5 2012-06-26 19:51:35
-3 also green

melikababadi 2012-06-26 19:51:39
-0 and 0 are equal therefore 0 cant be blue and red at the same time

Yasha 2012-06-26 19:51:46
Exactly, that's why it has to be green.

Yasha 2012-06-26 19:52:07
We can continue with this sort of logic, and we'll get a pattern:

Yasha 2012-06-26 19:52:11

Yasha 2012-06-26 19:52:16
What would have happened if we'd started with 1 being red?

yingted 2012-06-26 19:52:25
flip

bobthesmartypants 2012-06-26 19:52:32
red blue switcheroo

MA7HL0V3R 2012-06-26 19:52:37
The same pattern, with blue and red interchanged.

Watermelon876 2012-06-26 19:52:37
red and blue swapped, green stays the same

Yasha 2012-06-26 19:52:42
Right, we'd just get the same pattern with red and blue exchanged. (You can also think of it as exchanging positive and negative numbers.)

Yasha 2012-06-26 19:52:46

Yasha 2012-06-26 19:52:52
Are these two the only possible solutions aside from the trivial all-green solution?

yingted 2012-06-26 19:53:18
no

Watermelon876 2012-06-26 19:53:18
No!!!

Yasha 2012-06-26 19:53:25
Nope, we left out a case. What was it?

nemarci 2012-06-26 19:53:38
1 is green

Yasha 2012-06-26 19:53:48
We forgot to consider what would happen if 1 were green. If 1 is green, what do we know about 2?

bobthesmartypants 2012-06-26 19:54:08
nothing?

Yasha 2012-06-26 19:54:13
We don't know anything about 2, because none of our rules deal with green numbers. So 2 is free to be anything. Again, we'll assume it's blue.

Yasha 2012-06-26 19:54:22
Applying the rules as before, we can easily prove that the even numbers fit the pattern we saw above:

yingted 2012-06-26 19:54:26
double everything

Yasha 2012-06-26 19:54:31

Yasha 2012-06-26 19:54:36
But how can we fill in the odd numbers?

bobthesmartypants 2012-06-26 19:54:47
all green

Tonitruant 2012-06-26 19:54:47
Multiply everything by a constant, with the remaining numbers green.

yingted 2012-06-26 19:54:47
green

MA7HL0V3R 2012-06-26 19:54:51
They can all be green.

Yasha 2012-06-26 19:55:14
We could certainly make them all green. That wouldn't cause any contradictions, since the even numbers can only affect other even numbers by rules (I) and (II).

Yasha 2012-06-26 19:55:27
Are there any other ways to fill them in?

al87289 2012-06-26 19:55:41
no

Yasha 2012-06-26 19:55:54
Probably not. If we play around with it, it doesn't seem like we can.

Yasha 2012-06-26 19:55:59
Let's leave that issue aside for now, and come back to it later. So we've dealt with the case where 2 is our smallest positive non-green number. Are there any other cases?

MA7HL0V3R 2012-06-26 19:56:24
2 is red.

Yasha 2012-06-26 19:56:35
OK, so that just swaps everything.

spacebacon99 2012-06-26 19:56:44
2 is green

al87289 2012-06-26 19:56:44
3 is, and 4, and so on

Watermelon876 2012-06-26 19:56:44
3 is smallest nongreen, 4 is smallest nongreen, 5 is, ...

Tonitruant 2012-06-26 19:56:44
3 is our smallest positive non-green number, or any integer.

Yasha 2012-06-26 19:56:49
Sure. We could have 3 be our smallest positive non-green number, or 4, or 5, or any positive integer. And no matter which number it was, we'd get the same pattern for multiples of that number, with all three colors repeating.

Yasha 2012-06-26 19:57:03
What if there's no smallest positive non-green number?

yingted 2012-06-26 19:57:20
all green!

spacebacon99 2012-06-26 19:57:20
then all green

Tonitruant 2012-06-26 19:57:20
All green.

bobthesmartypants 2012-06-26 19:57:20
all greeen

Yasha 2012-06-26 19:57:25
Then we're in the all-green case. So this should be all of them, if we can deal with the issue of filling in non-multiples. Let's now state our claim about the general form of a legal coloring under these rules:

Yasha 2012-06-26 19:57:35

Yasha 2012-06-26 19:57:40

Yasha 2012-06-26 19:57:58
On our way, let's start with a lemma, which some of you mentioned already. What do you think is true of the sum of a red and blue number?

yingted 2012-06-26 19:58:12
green

Watermelon876 2012-06-26 19:58:13
green?

AwesomeToad 2012-06-26 19:58:13
green

Yasha 2012-06-26 19:58:21

Yasha 2012-06-26 19:58:29

Yasha 2012-06-26 19:58:40

Yasha 2012-06-26 19:58:55
Therefore, R + B must be green!

bobthesmartypants 2012-06-26 19:59:49
r+b=r+-r=0=green

Yasha 2012-06-26 19:59:51
Not quite. You're assuming there that b=-r, but b could be any blue number.

Yasha 2012-06-26 20:00:02
Now, suppose we're in the second case, and n is the smallest non-green positive integer. n is blue. So 2n must be red. By our lemma, 3n is green. 4n = 2n + 2n is blue. 5n = 4n + n must be red. 6n = 2n + 4n is green again.

Yasha 2012-06-26 20:00:09
But we won't get far coloring finitely many integers at a time. What tool should we use?

yingted 2012-06-26 20:00:21
mod or induction

Yasha 2012-06-26 20:00:25
Induction! Let's do induction on following statement:

Yasha 2012-06-26 20:00:29
(3k)n is green.
(3k + 1)n is blue.
(3k + 2)n is red.

Yasha 2012-06-26 20:00:34
We've done base cases for k = 0 and k = 1, so let's do the induction step. We assume the above statement is true for k, and prove it's true for k + 1.

spacebacon99 2012-06-26 20:01:22
what's induction?

Yasha 2012-06-26 20:01:24
Unfortunately, I can't explain it that quickly. There are AoPS classes you could take to learn about it.

Yasha 2012-06-26 20:01:34
(3(k + 1))n = (3k + 1)n + 2n, which is the sum of blue number and red number. So it must be green.

Yasha 2012-06-26 20:01:43
(3(k + 1) + 1)n = (3k + 2)n + 2n, which is the sum of two red numbers. So it must be blue.

Yasha 2012-06-26 20:01:50
Lastly, (3(k + 1) + 2)n = (3k + 1)n + 4n, which is the sum of two blue numbers. So it must be red.

Yasha 2012-06-26 20:01:58
Now we've dealt with all the positive multiples of n. What about the ones that aren't multiples of n? What do we want to be true about them?

Watermelon876 2012-06-26 20:02:14
They have to be green

yingted 2012-06-26 20:02:18
green

bobthesmartypants 2012-06-26 20:02:18
all green

Yasha 2012-06-26 20:02:25
We want to show they're all green. Well, let's use proof by contradiction and suppose they're not. Let m be the least positive non-green integer that is not a multiple of n. What must be true of m?

basketball8 2012-06-26 20:02:54
be blue

Yasha 2012-06-26 20:02:58
It could be blue or red.

yingted 2012-06-26 20:03:09
m>smallest non-green

Yasha 2012-06-26 20:03:16
Clearly m > n, since n was chosen to be the least positive non-green integer, period!

Yasha 2012-06-26 20:03:46
(Remember, we declared m to be the smallest positive non-green integer that is not a multiple of n.)

Yasha 2012-06-26 20:03:55
Is there a convenient way we could write m, keeping in mind that it's not a multiple of n?

yingted 2012-06-26 20:04:11
nk+d

Yasha 2012-06-26 20:04:21
Let m = qn + r, where 0 < r < n is the remainder when m is divided by n. We know this remainder is nonzero, since m is not a multiple of n. We also know that q > 0, since m > n.

Yasha 2012-06-26 20:04:36
Since m must be either blue or red, we should go through both cases and find a contradiction.

Yasha 2012-06-26 20:04:42
Suppose m is red. Then, because -n is red, we know m - n = (q - 1)n + r is blue, which gives us a smaller non-green positive integer that's not a multiple of n.

Yasha 2012-06-26 20:05:27
OK, so let's suppose m is blue. Since m is blue, and -2n is blue, m - 2n = (q - 2)n + r is red. If q > 1, this gives us a smaller positive non-green integer that's not a multiple of n, which is a contradiction. But there's one minor problem here. What is it?

Watermelon876 2012-06-26 20:05:44
q=1

Yasha 2012-06-26 20:06:24
Right, we only get a contradiction if we find a _positive_ non-green integer smaller than n.

Yasha 2012-06-26 20:06:36
We might fall into the negatives, if q = 1!

nemarci 2012-06-26 20:06:53
if q=1, then (q-2)n+r=-n+r is red, then n-r is blue

Yasha 2012-06-26 20:06:56
But if q = 1, and m - 2n = -n + r is red, that means that n - r is blue by (I), another contradiction. Whew.

Yasha 2012-06-26 20:07:09
Now, we've shown that all the positive numbers which are multiples of n follow the mod 3 pattern, and all the ones which aren't multiples of n must be green. Do we need to show the same for negative numbers?

nemarci 2012-06-26 20:07:42
no, because of symmetry

Watermelon876 2012-06-26 20:07:42
no because each neg corresponds to a positive nongreen which is it's negative

Yasha 2012-06-26 20:07:47
No! Rule (I) handles that all for us. So we're done.

Yasha 2012-06-26 20:07:59
Questions before we go on?

Watermelon876 2012-06-26 20:08:19
This was so cool. I never realized that R+B was green

Yasha 2012-06-26 20:08:21
Yup, it's a pretty cool problem.

Yasha 2012-06-26 20:08:27
Problem 3: Campers in a circle with cookies.

Yasha 2012-06-26 20:08:38

Yasha 2012-06-26 20:09:03
Ah, one sec, a question on the previous problem:

viperstrike 2012-06-26 20:09:06
there are provable rules which apply to the green numbers which limit the possible solutions to all green and the alternating green red blue arrangements can you write a full solutions in sumary please

Yasha 2012-06-26 20:09:45
So the solutions are either all green, or there is some n where multiples of n cycle blue, red, green, and all non-multiples of n are green.

Yasha 2012-06-26 20:10:06
Of course, to get full credit, you need a proof, which is what we came up with earlier.

Yasha 2012-06-26 20:10:30
OK, anyways, on to problem 3.

Yasha 2012-06-26 20:10:46
Before we go any further, let's try some small cases so we get an idea of what's going on. The smallest case to try is p=3. What are the labels of the campers who get cookies, in order?

Watermelon876 2012-06-26 20:12:00
1,2,1,1,2,1,...

nemarci 2012-06-26 20:12:00
1;2;1;1;2;1;1;2;1...

xsad1300 2012-06-26 20:12:00
12112112112112112

AwesomeToad 2012-06-26 20:12:00
1, 2, 1, 1, 2, 1, ...

Yasha 2012-06-26 20:12:11
First camper 1 says 1, then camper 2, says 2. We skip over camper 3 and go back to camper 1, who says 3. Three spaces around the circle gets us back around to camper 1 again, who says 4. Continuing, we see that the sequence of campers who get cookies is 1, 2, 1, 1, 2, 1, 1, 2, 1, and so forth, repeating every three.

marupiravi 2012-06-26 20:12:23
the smallest case we can try is case p=1

Yasha 2012-06-26 20:12:24
Ah, nope, 1 is not considered to be a prime.

Yasha 2012-06-26 20:12:32
What about if p=5? What's the sequence of camper labels then?

viperstrike 2012-06-26 20:12:55
1,2,4,2,1

nemarci 2012-06-26 20:12:55
1;2;4;2;1;1;2;4;2;1...

Yasha 2012-06-26 20:13:01
With p=5, we can compute that the sequence of campers who get cookies is 1, 2, 4, 2, 1, 1, 2, 4, 2, 1, and so forth, repeating every five. What about if p=7?

spacebacon99 2012-06-26 20:13:25
1,2,4,7,4,2,1

yingted 2012-06-26 20:13:25
1247421

Mr.117 2012-06-26 20:13:25
1, 2, 4, 7, 4, 2, 1

Yasha 2012-06-26 20:13:31
With p=7, the sequence is 1, 2, 4, 7, 4, 2, 1, 1, 2, 4, 7, 4, 2, 1, and so forth, repeating every seven.

Yasha 2012-06-26 20:13:35
Any questions so far?

spacebacon99 2012-06-26 20:14:01
why the pattern?

Yasha 2012-06-26 20:14:05
We'll find out!

upleit 2012-06-26 20:14:08
why is there a 7 after 1,2, and 4

Yasha 2012-06-26 20:14:29
camper number 4 says 3, so you move three spots down the circle to camper number 7.

Yasha 2012-06-26 20:14:51
OK, keeping our examples in mind, let's tackle the problem:

Yasha 2012-06-26 20:14:55
(a) Show that there is a camper who never gets a cookie.

Yasha 2012-06-26 20:15:03
Looking at our examples, what can we do?

spacebacon99 2012-06-26 20:15:33
camper 3 never gets cookie

Yasha 2012-06-26 20:15:38
It looks like camper 3 never gets a cookie, but it turns out that if we were to try more examples, we'd find a value for p where camper 3 does get a cookie. For example, if p=13, then the sequence of campers is 1, 2, 4, 7, 11, 3, 9, 3, 11, 7, 4, 2, 1, and then it repeats.

Watermelon876 2012-06-26 20:16:11
we can show that camper 1 recieves at least two cookies. Or more generally that it's symmetric

yingted 2012-06-26 20:16:11
show one camper always gets more than one

Yasha 2012-06-26 20:16:18
Based on our examples, it looks like the sequence of campers getting cookies repeats every p cookies, and it looks like camper 1 gets the first and last cookie in each repeating block. Since there are p cookies given out each block and there are p campers, if camper 1 gets two cookies in a block, then that means some other camper has to have gotten no cookies.

nemarci 2012-06-26 20:16:28
in every period, 1 gets the first and last cookie

yingted 2012-06-26 20:16:32
since camper 1 always gets at least 2, some camper can't get any :(

vlchen888 2012-06-26 20:16:53
how can u prove the pattern though?

Yasha 2012-06-26 20:16:58
Don't worry, we'll get there.

upleit 2012-06-26 20:17:23
So, it circulates, and everybody ends up getting a cookie, right?

Yasha 2012-06-26 20:17:26
Nope, it looks like not everyone gets a cookie, and some people get lots of them.

Yasha 2012-06-26 20:17:36
Let's see if we can prove our hunches. First, can anyone find a way to determine the label of the camper who says the number n, in terms of n?

nemarci 2012-06-26 20:18:09
1+n(n-1)/2

Maz906 2012-06-26 20:18:23
a_n = 1 + T_(n-1), where T_n is the nth triangular number, and a_n is the label of the camper that shouts n

MA7HL0V3R 2012-06-26 20:18:27
Camper = n(n-1)/2+1 (mod p)

viperstrike 2012-06-26 20:18:33
n(n-1)/2 +1

Mr.117 2012-06-26 20:18:33
1+(n-1)(n-2)/2

viperstrike 2012-06-26 20:18:33
mode p

Yasha 2012-06-26 20:18:36

Yasha 2012-06-26 20:18:47
We'd like to show that the sequence of campers who speak is periodic with period p. That is, if a camper says n, then that camper will also say n+p.

Yasha 2012-06-26 20:19:07
How can we show that this statement is true?

bobthesmartypants 2012-06-26 20:19:26
mod

Yasha 2012-06-26 20:19:35
We could use some facts from modular arithmetic.

nemarci 2012-06-26 20:19:38
p(p-1)/2 is evenly divisible by p, because p-1 is even

Yasha 2012-06-26 20:19:48
We could also do it directly.

Yasha 2012-06-26 20:19:55

Yasha 2012-06-26 20:20:04

Yasha 2012-06-26 20:20:16

Yasha 2012-06-26 20:20:29
We conclude that the camper who says n also says n+p, so the sequence of campers who speak is periodic with period p.

Yasha 2012-06-26 20:20:37
Now, all we have left to show is that camper 1 gets two cookies in each repeating block, and from there we'll be able to conclude that some other camper must get no cookies.

Yasha 2012-06-26 20:20:51
How can we show that camper 1 gets two cookies in each round of p cookies?

bobthesmartypants 2012-06-26 20:21:18
symmetry

Yasha 2012-06-26 20:21:36
Alas, we haven't proved symmetry yet. Proving symmetry will suffice to do it.

marupiravi 2012-06-26 20:21:53
p=3

marupiravi 2012-06-26 20:21:53
because it will be 1,2,1

Yasha 2012-06-26 20:22:06
Yeah, it's easy to see for p=3, but we need to prove it for all values of p.

yingted 2012-06-26 20:22:34
he also gets the pth

yingted 2012-06-26 20:22:34
/she

vlchen888 2012-06-26 20:22:34
plug p into the equation

yingted 2012-06-26 20:22:34
if someone gets the pth cookie, they also get the (p+1)th cookie

Yasha 2012-06-26 20:23:06
So, we can be clever and notice that whoever says p also says the next number, since going p spaces around the circle gets you back to where you started.

Yasha 2012-06-26 20:23:20
We proved periodicity, so we know that camper 1 says p+1, so therefore camper 1 must say p.

Yasha 2012-06-26 20:23:44
However, even without a clever argument, you can still just plug p into the formula.

Yasha 2012-06-26 20:23:55

upleit 2012-06-26 20:24:17
Can other campers stil get more than 1 cookie?

Yasha 2012-06-26 20:24:28
Yes, in fact it seems like they do, from our examples.

bobthesmartypants 2012-06-26 20:24:43
wouldn't (p-1)/2 people get at least 2 cookies?

Yasha 2012-06-26 20:24:51
It sure looks that way, but we haven't proved it yet.

Yasha 2012-06-26 20:25:03
We showed that camper 1 gets two cookies in the first p turns. In the first p turns, there are p cookies to be distributed among p campers. If camper 1 gets two cookies, that means that some other camper must have gotten no cookies in the first p turns.

Yasha 2012-06-26 20:25:13
But we showed that the campers who speak are periodic with period p. Therefore, if a camper doesn't get a cookie in the first p turns, that camper will never get a cookie.

Yasha 2012-06-26 20:25:16
:(

marupiravi 2012-06-26 20:25:44
we can prove it with the example in the begginging

marupiravi 2012-06-26 20:25:44
of p=13

Yasha 2012-06-26 20:26:00
Again, that will just prove it for p=13, but we wouldn't know if it is true for p=17.

Yasha 2012-06-26 20:26:05
Or for p=997.

Yasha 2012-06-26 20:26:26
Maybe it stops being true once p gets big enough.

Yasha 2012-06-26 20:26:33
Until we prove it, it's just a hunch.

yingted 2012-06-26 20:26:45
what are we trying to show?

Yasha 2012-06-26 20:26:53
We were trying to show that some camper gets no cookies.

Yasha 2012-06-26 20:27:05
We're done with that now, so we're about to move to the next part.

upleit 2012-06-26 20:27:21
Is it possible to get an example that takes care of all cases?

Yasha 2012-06-26 20:27:23
Sometimes that's possible, but not in this problem.

jared429 2012-06-26 20:27:45
is there anything special about it being prime, or would it work if p were just some odd number?

Yasha 2012-06-26 20:27:47
Yes, there is something special about p being prime, though I don't think we've used it yet.

Yasha 2012-06-26 20:28:16
(b) Of the campers who do get cookies, is there one who at some point has at least ten more cookies than the others?

Yasha 2012-06-26 20:28:31
Based on our examples, what do we think the answer is?

Watermelon876 2012-06-26 20:28:55
No except if p=3

bobthesmartypants 2012-06-26 20:28:56
no

nemarci 2012-06-26 20:28:56
no

Yasha 2012-06-26 20:29:01
It looks like, in each block of p cookies, some campers get no cookies, some campers get two cookies, and one camper gets one cookie. For p>3, it looks like there are at least two campers who get two cookies each block, so none of them can get far ahead of all of the others. The answer seems to be no.

Yasha 2012-06-26 20:29:35
So just to be clear about the question: It is true that some campers get ahead of some other campers, but no camper gets ahead of all of the other campers.

Yasha 2012-06-26 20:29:53
When p=3, the sequence of campers who get cookies is 1, 2, 1, 1, 2, 1, and so forth. Camper 1 gets two cookies each block, camper 2 gets one cookie each block, and camper 3 gets no cookies. Therefore, after thirty turns, camper 1 will have twenty cookies, and camper 2 will have ten cookies. For p=3, the answer is yes.

Yasha 2012-06-26 20:30:17
OK, so now we still have to prove our theory that some campers get two cookies, some campers get no cookies, and one camper gets one cookie.

upleit 2012-06-26 20:30:43
So, it's only if p is smaller than 3?

Yasha 2012-06-26 20:31:08
There's only one odd prime less than or equal to 3, namely 3 itself. For p=3, the answer is yes. Otherwise, it is no.

Yasha 2012-06-26 20:31:44
Let's look at one of our examples again, with p=13: The sequence of campers who speak is 1, 2, 4, 7, 11, 3, 9, 3, 11, 7, 4, 2, 1, and then it repeats.

Yasha 2012-06-26 20:31:53
Lots of people have noticed that there is symmetry.

vlchen888 2012-06-26 20:31:57
the middle guy gets 1 cookie

Yasha 2012-06-26 20:32:19
Also, you can notice that the person who says the "middle" number is the one who only gets one cookie per block of p cookies.

marupiravi 2012-06-26 20:32:46
once angaing can you prove it with other numbers

Yasha 2012-06-26 20:33:02
We'll get there. We're looking at an example to get an idea for how to prove it, and then we'll prove it for all odd primes.

Yasha 2012-06-26 20:33:49
Anyways, the sequence seems to be a palindrome, which means that it is the same when read forwards and backwards. Can we prove that the sequence is always a palindrome, no matter what p is?

vlchen888 2012-06-26 20:34:17
with mod?

upleit 2012-06-26 20:34:17
yes

Watermelon876 2012-06-26 20:34:17
Yes; Modular arithmetic does the trick

Yasha 2012-06-26 20:34:32
Sure, we could use modular arithmetic. We don't necessarily need it: our formula is enough.

Yasha 2012-06-26 20:34:46
To show that the sequence is a palindrome, we have to show that the camper who says n also says p+1-n. (Check a few values of n in our example to convince yourself that p+1-n is the right formula for the "mirror image" of n in our palindrome.)

Yasha 2012-06-26 20:35:05
To do this, we can use our formula.

Yasha 2012-06-26 20:35:18

Yasha 2012-06-26 20:35:25

Yasha 2012-06-26 20:35:40

Yasha 2012-06-26 20:35:50
OK, so we know that the sequence of campers who say the first p numbers is a palindrome. Therefore, a camper who speaks in the first block of p numbers will speak a second time in that block, except for the camper who speaks in the exact middle of the block. (In our example with p=13, that camper was labeled 9.)

Yasha 2012-06-26 20:36:01
Are we done? Have we successfully shown that some campers speak exactly twice, and one camper speaks exactly once?

Mr.117 2012-06-26 20:36:14
have we proved the numbers in the palindrome only appear once/twice and not more?

Yasha 2012-06-26 20:36:32
Aha, that's the issue that we haven't yet dealt with.

Yasha 2012-06-26 20:36:41
We haven't ruled out the case where a camper speaks three times, or four times. What if the sequence instead looked like 1, 2, 4, 9, 11, 3, 9, 3, 11, 9, 4, 2, 1? Or 1, 2, 3, 7, 11, 3, 9, 3, 11, 7, 3, 2, 1? It's still a palindrome, but there is one camper that speaks more than twice and will eventually have ten more cookies than anyone else. We need to rule out this possibility.

yingted 2012-06-26 20:36:58
consider 15

Yasha 2012-06-26 20:37:20
Apparently, this happens if you try p=15, according to yingted.

nemarci 2012-06-26 20:37:28
15 is not prime

bobthesmartypants 2012-06-26 20:37:28
not a prime

Yasha 2012-06-26 20:37:30
Fortunately for us, 15 is not a prime.

Yasha 2012-06-26 20:37:47
This answers the earlier question of whether or not it matters that p is prime.

Yasha 2012-06-26 20:37:56

Yasha 2012-06-26 20:38:05

Yasha 2012-06-26 20:38:12
A value of n satisfies this equation if and only camper c says the number n.

Yasha 2012-06-26 20:38:16
What does this equation look like?

Watermelon876 2012-06-26 20:38:28
A quadratic equation!

Yasha 2012-06-26 20:38:33
It looks like a quadratic equation in n. What do we know about quadratic equations, at least when dealing with real numbers?

yingted 2012-06-26 20:39:05
<=2 solutions

MA7HL0V3R 2012-06-26 20:39:05
They have at most two roots.

nemarci 2012-06-26 20:39:05
they don't have more than 2 solutions

Yasha 2012-06-26 20:39:11
Quadratic equations over the real numbers have at most two solutions. This fact is also true over the integers mod p, if p is a prime. (In fact, quadratic equations have at most two solutions over any field, but don't worry if you haven't heard of fields before.)

Yasha 2012-06-26 20:39:42
There's also a way to do this problem without using this fact, but I'm going to use it to save time.

Yasha 2012-06-26 20:39:57

bobthesmartypants 2012-06-26 20:40:21
there can be 2 solutions at most

bobthesmartypants 2012-06-26 20:40:24
not over 2

Yasha 2012-06-26 20:40:31
The camper c says the number n if and only if that equation is satisfied. Therefore, in the first p turns, camper c will speak at most twice.

Yasha 2012-06-26 20:40:36
We showed that the sequence of campers who say the first p numbers is a palindrome. How can we use the fact that no camper speaks more than twice to finish the problem?

Yasha 2012-06-26 20:41:20

Yasha 2012-06-26 20:41:26
Since no camper can speak more than twice in a block, the campers who get the most cookies are the ones who do speak twice.

nemarci 2012-06-26 20:41:37
if p>=5, then there are more than 1 campers who get 2 cookies, but no one gets more

Yasha 2012-06-26 20:41:48
Exactly. For p>3, there are at least two numbers in the first half of the palindrome, and the campers who say those numbers have to different. (If a camper were to say two numbers in the first half of the palindrome, they would have to also say two numbers in the second half of the palindrome, for a total of four times.)

Tonitruant 2012-06-26 20:41:55
And there are (p-1)/2 of them.

Yasha 2012-06-26 20:42:09
Yes.

bobthesmartypants 2012-06-26 20:42:16
and there are more than one 2-cookie camper in p<=5

Yasha 2012-06-26 20:42:23
Ah, nope, not for p=3, as we've seen.

bobthesmartypants 2012-06-26 20:42:39
sorry, typo

bobthesmartypants 2012-06-26 20:42:44
p>=5

Yasha 2012-06-26 20:42:47
ah ok.

Yasha 2012-06-26 20:43:00
There are at least two campers who speak twice, and so they can't get far ahead of all the others in terms of number of cookies.

Yasha 2012-06-26 20:43:26
Any questions on this part?

Yasha 2012-06-26 20:43:36
(c) Of the campers who do get cookies, is there one who at some point has at least ten fewer cookies than the others?

Yasha 2012-06-26 20:43:45
Based on our work, what is the answer?

bobthesmartypants 2012-06-26 20:43:59
yes

Watermelon876 2012-06-26 20:43:59
yes

nemarci 2012-06-26 20:43:59
yes

bobthesmartypants 2012-06-26 20:43:59
the one who gets one cookie

yingted 2012-06-26 20:43:59
yes

Yasha 2012-06-26 20:44:04

Yasha 2012-06-26 20:44:12
All of the other campers who speak get two cookies in the first block of p numbers, since a camper who says a number in the first half of the palindrome also says a number in the second half, and vice versa.

Yasha 2012-06-26 20:44:21
Therefore, after ten blocks of p numbers, the camper who said (p+1)/2 will have ten cookies, whereas all of the other campers who got cookies will have twenty of them.

Watermelon876 2012-06-26 20:45:36
In the interest of saving time, maybe we can take a poll and find out which problems/sections people want to see. I only need to see 4 and 6 (maybe 5f). Anything else is just extra. Similarly I'm sure some people only need to see 5de or something...

Yasha 2012-06-26 20:45:38
Yes, as you can tell, we're going to run a bit over, which is fine. However, since some people might need to leave, I'd be up for switching up the order. How about we take a vote on which problem to see next. If there's a clear winner, I'll go with that, and if not I'll just move on to 4.

bobthesmartypants 2012-06-26 20:46:32
what is this for?

bobthesmartypants 2012-06-26 20:46:32
I just randomly joined

Yasha 2012-06-26 20:46:44
Ah, these are the Mathcamp qualifying quiz problems.

Yasha 2012-06-26 20:47:28
There's no clear consensus, so I'm going to move on to 4.

Yasha 2012-06-26 20:47:41
There will be a transcript at the end, so if you have to leave you can look back at it tomorrow.

Yasha 2012-06-26 20:47:50
Problem 4: Lollipops.

Yasha 2012-06-26 20:47:56
Let a be a rational number with 0 < a < 1. A lollipop in the xy-plane with base (a,0) consists of a line segment from (a,0) to some point (a,b) with b > 0, together with a filled in disc of radius less than b, centered at (a,b). Determine whether or not it is possible to have a set of lollipops in the xy-plane satisfying both of the following conditions:
* for every rational number a with 0 < a < 1, there is a lollipop whose base is the point (a,0),
* no two lollipops touch or overlap each other.
If such a set of lollipops exists, explain how to construct it. If not, justify why not.

Yasha 2012-06-26 20:48:23
First, are there any questions about what a lollipop is?

Watermelon876 2012-06-26 20:49:10
You could just troll and say that the radius is 0 I guess

Yasha 2012-06-26 20:49:13
True, so we assume that the radius has to be positive.

Yasha 2012-06-26 20:49:21
So, our task to construct a non-overlapping set of lollipops with bases at every rational number between 0 and 1. Or prove that it's impossible. How many lollipops is that?

jared429 2012-06-26 20:49:42
infinite

robinpark 2012-06-26 20:49:43
infinite

Watermelon876 2012-06-26 20:49:43
aleph-null

bobthesmartypants 2012-06-26 20:49:43
rational number? there are infinite of those

MA7HL0V3R 2012-06-26 20:49:46
Infinite number.

Global 2012-06-26 20:49:49
infinitely many

Yasha 2012-06-26 20:49:54
Yes, there are infinitely many. (In fact, the rationals between 0 and 1 form a countably infinite set.) Hmm, that's going to make things tough. We need to find some way to deal with this huge set of numbers.

Yasha 2012-06-26 20:50:02

Yasha 2012-06-26 20:50:06
It would be really convenient if we knew where to start. Is there a natural order to consider these numbers in? (That is, does S have a least element?)

bobthesmartypants 2012-06-26 20:50:32
0

Yasha 2012-06-26 20:50:33
Nope, it says 0<r.

Maz906 2012-06-26 20:50:40
...no?

robinpark 2012-06-26 20:50:40
S doesn't have a least element.

Yasha 2012-06-26 20:50:51
Unfortunately, the standard order of numbers is not going to be helpful. What's the first positive rational number?

Mr.117 2012-06-26 20:51:05
infinitely small...

Yasha 2012-06-26 20:51:09

Yasha 2012-06-26 20:51:20
Is there a better way to put S in order?

yingted 2012-06-26 20:51:37
by denominato

yingted 2012-06-26 20:51:37
you need to minimize the denominator, then the numerator

nemarci 2012-06-26 20:51:37
yes, we can put the elements of S into an order, similarly to 1c

Tonitruant 2012-06-26 20:51:37
Use the spiral method from the frog problem.

yingted 2012-06-26 20:51:39
by denominator

Yasha 2012-06-26 20:51:44
Right, we can sort them by denominator. First 1/2, then 1/3 and 2/3, then 1/4 and 3/4, then 1/5, 2/5, 3/5, and 4/5...

Yasha 2012-06-26 20:51:54
To make this more precise, each element of S can be written in lowest terms as p/q, where p and q have no common factors.

Yasha 2012-06-26 20:51:58

Yasha 2012-06-26 20:52:02

Yasha 2012-06-26 20:52:07

Yasha 2012-06-26 20:52:11

Yasha 2012-06-26 20:52:15

Yasha 2012-06-26 20:52:19
And so on.

Yasha 2012-06-26 20:52:22

Yasha 2012-06-26 20:52:28

Yasha 2012-06-26 20:52:35
Can our set of lollipops all be the same height?

yingted 2012-06-26 20:52:45
no

Watermelon876 2012-06-26 20:52:45
no

Global 2012-06-26 20:52:49
no

Mr.117 2012-06-26 20:52:49
no

bobthesmartypants 2012-06-26 20:52:49
no

Yasha 2012-06-26 20:52:56
No, that definitely won't work. If they're all the same height, then the discs will certainly overlap.

Yasha 2012-06-26 20:53:05
So what should we do with the heights as we go along? We could have them increase or decrease. (Or something more complicated, of course, but let's start with those.)

Yasha 2012-06-26 20:53:29
Which makes more sense, increasing heights or decreasing heights?

Watermelon876 2012-06-26 20:53:57
Decreasing actually makes more sense

Mr.117 2012-06-26 20:53:57
decreasing...

AwesomeToad 2012-06-26 20:53:57
decreasing?

Yasha 2012-06-26 20:54:01
Increasing heights won't help us. Once we have a lollipop of radius c > 0 based at 1/2, then any taller lollipop based at a number within c of 1/2 is going to overlap.

Watermelon876 2012-06-26 20:54:08
If we decrease, we don't have a chance of the stalk of the lollipop colliding with a disc

Yasha 2012-06-26 20:54:21
So we want the lollipops to be shorter and shorter as the denominator increases.

Yasha 2012-06-26 20:54:26

yingted 2012-06-26 20:54:50
make the top below the bottom

Yasha 2012-06-26 20:54:55

bobthesmartypants 2012-06-26 20:55:10
make them just below touching

Yasha 2012-06-26 20:55:13

Yasha 2012-06-26 20:55:24

Yasha 2012-06-26 20:55:42
yingted has provided us with a pretty awesome illustration:

yingted 2012-06-26 20:55:44

Yasha 2012-06-26 20:56:19
Again, let's make this precise. What a good way to divide the positive y-axis into infinitely many disjoint intervals that go to zero?

yingted 2012-06-26 20:57:11
1/denominator

Watermelon876 2012-06-26 20:57:11
geometric series?

Mr.117 2012-06-26 20:57:11
by denominators.

nemarci 2012-06-26 20:57:11
1/2; 1/4; 1/8; 1/16 ...

Yasha 2012-06-26 20:57:17

Yasha 2012-06-26 20:57:21

Yasha 2012-06-26 20:57:25

Yasha 2012-06-26 20:57:30

Yasha 2012-06-26 20:57:33
And so on.

Yasha 2012-06-26 20:57:41

Yasha 2012-06-26 20:57:48

Yasha 2012-06-26 20:58:03
For example, the lollipop on 1/2 is centered at (1/2, 3/4) and has radius 1/4. So the y-values of the disc are all between 1/2 and 1.

Yasha 2012-06-26 20:58:07
The lollipops on 1/3 and 2/3 are centered at (1/3, 5/12) and (2/3, 5/12) and have radius 1/12. So the y-values of the discs are all between 1/3 and 1/2.

Yasha 2012-06-26 20:58:12
Now we're guaranteed that lollipops in different layers won't have their discs overlap.

Yasha 2012-06-26 20:58:16
What about lollipops within the same layer?

marupiravi 2012-06-26 20:58:36
they will not touch

Yasha 2012-06-26 20:58:46

bobthesmartypants 2012-06-26 20:58:50
their distance is greater then their combined diameters

yingted 2012-06-26 20:58:54
they are too small to touch

Watermelon876 2012-06-26 20:58:54
too far apart. The closest they could be is within 1/(q-1) of each other and the radius is less

Yasha 2012-06-26 20:59:05
(Unless, of course, q = 2, but in that case there's only one lollipop in the layer!)

Yasha 2012-06-26 20:59:11
So lollipops in the same layer can't have overlapping discs either.

Yasha 2012-06-26 20:59:16
Are we done?

Yasha 2012-06-26 20:59:53
No! There's one other issue to deal with: the possible overlap between discs and the vertical line segments. We haven't dealt with that possibility at all.

nemarci 2012-06-26 21:00:02
no, because circles can cross line segments parallel with y-axis

Yasha 2012-06-26 21:00:06
Suppose we have a lollipop whose disc intersects some vertical segment belonging to a second lollipop. Which one is taller, the first or the second lollipop?

Watermelon876 2012-06-26 21:00:21
the second

MA7HL0V3R 2012-06-26 21:00:26
second

bobthesmartypants 2012-06-26 21:00:33
2nd

Yasha 2012-06-26 21:00:35

yingted 2012-06-26 21:00:58
anything q'<q

Yasha 2012-06-26 21:01:01

Yasha 2012-06-26 21:01:06
Now, since there are only finitely many lollipops taller than any given lollipop, we could simply shrink each radius so that it doesn't touch any of their stems.

Yasha 2012-06-26 21:01:13

Yasha 2012-06-26 21:01:18
Let's prove it.

Yasha 2012-06-26 21:01:24

Yasha 2012-06-26 21:01:31
How can we find out whether this happens?

yingted 2012-06-26 21:02:31
subtraction

Yasha 2012-06-26 21:02:36

bobthesmartypants 2012-06-26 21:03:12
They do not overlap!

Yasha 2012-06-26 21:03:15

Yasha 2012-06-26 21:03:23
The first inequality is true because the distance can't be zero, so the numerator has absolute value at least one. And the following one is true because n < q, so n is at most q - 1.

Yasha 2012-06-26 21:03:33

Yasha 2012-06-26 21:03:41
We proved earlier that there were no overlaps between discs and discs, and obviously two stems will never overlap, so our construction works and we're done!

Yasha 2012-06-26 21:03:43
Yay!

Yasha 2012-06-26 21:03:52
Any questions on this problem?

bobthesmartypants 2012-06-26 21:04:27
I have a question: What grade is this? I'm in 6th

Yasha 2012-06-26 21:04:35
Mathcamp is a summer program for people 13 and above.

Watermelon876 2012-06-26 21:04:58
I propose we move on to 6 and skip 5

Yasha 2012-06-26 21:05:14
Some people wanted to see 5 though, so I think we'll go in order.

Technik 2012-06-26 21:05:18
What is this MathJam?

Yasha 2012-06-26 21:05:25
This is the Mathcamp qualifying quiz Mathjam.

Yasha 2012-06-26 21:05:33
Problem 5: P-distances.

Yasha 2012-06-26 21:05:38
A convex body in the plane is a region with positive area such that for any two points in this region, the entire line segment between them also lies within the region. Let P be the perimeter (i.e., boundary) of a convex body in the plane. We will assume throughout this problem that P is centrally symmetric: that is, if (a,b) is a point on P, then so is (-a,-b).

Yasha 2012-06-26 21:05:42
For any nonnegative real number k, we define kP to be the subset of the plane obtained by multiplying all the points of P by k in each coordinate. In other words, for each point (a,b) of P, the point (ka,kb) is in kP.

Yasha 2012-06-26 21:05:46
If (x_1,y_1), (x_2,y_2) are two points in the plane, we define the P-distance between them to be the smallest nonnegative real number k such that when the set kP is translated by (x_1,y_1) (that is, by x_1 units horizontally and by y_1 units vertically), the point (x_2,y_2) lies on it. For example, suppose that P is the square with vertices (0,1), (1,0), (0,-1), (-1,0); then the P-distance between (3,5) and (4,10) is 6.

Yasha 2012-06-26 21:06:24
Before we start trying to prove part (a), let's make some observations about the notion of P-distance.

Yasha 2012-06-26 21:06:30

yingted 2012-06-26 21:06:53
yes

yingted 2012-06-26 21:06:57
f(x_1-x_2,y_1-y_2)

Watermelon876 2012-06-26 21:07:03
P-distance is in terms of a shape

nemarci 2012-06-26 21:07:06
the P-distance of (0;0) and (x_2-x_1;y_2-y_1)

Yasha 2012-06-26 21:07:12

Yasha 2012-06-26 21:07:20
So right off the bat, we can just think about P-distances from the origin. That means no translations are necessary; the P-distance between (0,0) and (x,y) is just the smallest factor of k such that kP contains (x,y).

Yasha 2012-06-26 21:07:30
How can we find this k?

yingted 2012-06-26 21:07:55
magnitude divided by projection

Global 2012-06-26 21:07:55
write P as a polar curve r=r(\theta)

Yasha 2012-06-26 21:08:12
We could write P as a polar curve, but you can do it without that.

Yasha 2012-06-26 21:08:17
We can draw a ray from the origin to (x,y), and see where that ray intersects P.

Yasha 2012-06-26 21:08:21
Suppose the ray from the origin to (x,y) intersects P in a point p. Then what is the P-distance between the origin and (x,y)?

yingted 2012-06-26 21:08:51
or for an intuitive approximation, draw several shapes for each integer k

Global 2012-06-26 21:08:55
yes; describe P as a polar curve, and use the radius

Global 2012-06-26 21:08:55
then, if tan \theta = y/x, the P-distance between origin and (x,y) is \sqrt(x^2+y^2)/r(\theta)

yingted 2012-06-26 21:08:57
(x,y)/p

Yasha 2012-06-26 21:09:06

Yasha 2012-06-26 21:09:18
(Here, we're using d(p,q) to mean normal Euclidean distance between the points p and q.)

Yasha 2012-06-26 21:09:22
There's one subtlety here: how do we know that the ray intersects the perimeter P in only one point?

yingted 2012-06-26 21:09:37
convex

MA7HL0V3R 2012-06-26 21:09:41
P is convex.

Yasha 2012-06-26 21:09:46
We have to use convexity. It's not hard, so I'll leave the details to you.

Yasha 2012-06-26 21:09:50
Okay, now let's tackle part (a).

Yasha 2012-06-26 21:09:58
(a) Let P be the perimeter of a disc of radius 1 centered at the origin. Find a formula for the P-distance between any two points (a,b) and (c,d) in the plane.

Yasha 2012-06-26 21:10:15
By our previous work, we just need the P-distance between the origin and (a - c, b - d).

Yasha 2012-06-26 21:10:19
What is that distance?

nemarci 2012-06-26 21:10:38
it equals the normal distance

Watermelon876 2012-06-26 21:10:38
d(a - c, b - d)

yingted 2012-06-26 21:10:38
euclidean

Yasha 2012-06-26 21:10:42
It doesn't matter where the ray intersects the disc, since for all points on the perimeter of the disc, d((0,0), p) = 1. That's the definition of a disc!

Yasha 2012-06-26 21:10:49

Yasha 2012-06-26 21:10:59
(b) Let P be the perimeter of a rhombus with vertices (2,0), (-2,0), (0,3), (0,-3). Find a formula for the P-distance between any two points (a,b) and (c,d) in the plane.

Yasha 2012-06-26 21:11:09
Can we save ourselves some trouble here by narrowing our cases?

nemarci 2012-06-26 21:11:36
study just one quarter of the plane

Watermelon876 2012-06-26 21:11:42
Yes, consider only first quadrant for now

Yasha 2012-06-26 21:11:46
By symmetry of the rhombus, we can get most of our information from the case where (a - c, b - d) is in the first quadrant. What's the equation for the line which is the portion of P in the first quadrant?

bobthesmartypants 2012-06-26 21:12:11
assuming that the center of the rhombus is at 0,0?

Yasha 2012-06-26 21:12:25
Yup, when we compute the distance from the origin, we don' tneed to translate.

MA7HL0V3R 2012-06-26 21:12:42
y=-3/2x+3

nemarci 2012-06-26 21:12:42
3x+2y=6

Yasha 2012-06-26 21:12:47
It's just 3x + 2y = 6.

Yasha 2012-06-26 21:12:51
When we scale this by a factor of k, what do we get?

nemarci 2012-06-26 21:13:12
3x+2y=6k

Yasha 2012-06-26 21:13:18
Right, 3x + 2y = 6k.

Yasha 2012-06-26 21:13:31
And if we want (a - c, b - d) to lie on this line, what should we do?

Maz906 2012-06-26 21:14:07
substitute that in and solve for k

bobthesmartypants 2012-06-26 21:14:07
replace x and y with the variables?

Global 2012-06-26 21:14:07
3(a-c)+2(b-d)=6k

adi12 2012-06-26 21:14:21
3(a-c)+2(b-d)=6k

Yasha 2012-06-26 21:14:24
We just plug them in to get 3(a - c) + 2(b - d) = 6k.

Yasha 2012-06-26 21:14:29

Yasha 2012-06-26 21:14:34
What if a - c is negative?

nemarci 2012-06-26 21:15:00
then use c-a

Global 2012-06-26 21:15:00
use symmetry of rhombus for other cases

MA7HL0V3R 2012-06-26 21:15:00
Use absolute values?

Watermelon876 2012-06-26 21:15:00
turns out if we drop absolute value bars around both terms, stuff works out

Yasha 2012-06-26 21:15:11
Then the x-coefficient in the equation for the line would also be negative, so it would still have a positive contribution to the distance.

yingted 2012-06-26 21:15:15
abs

Yasha 2012-06-26 21:15:22

Yasha 2012-06-26 21:15:29
(c) In part (a), we took it for granted that a filled-in disc of radius 1 is a convex body. Prove this rigorously, using the definition of convexity given above.

Yasha 2012-06-26 21:15:58
So we want to prove that, for any two points p and q in a disc of radius 1, every point r on the line segment connecting p to q is still within the disc.

Yasha 2012-06-26 21:16:05
Can we make any sort of assumptions about p and q to cut down the possibilities?

bobthesmartypants 2012-06-26 21:16:39
the circle doesn't have any part where it caves in

Yasha 2012-06-26 21:16:40
Yup, but we want to prove it rigorously.

Yasha 2012-06-26 21:16:58
If we extend the the line pq, it'll hit the boundary circle on both sides. So without loss of generality, it suffices to prove that r is in the disc whenever p and q are on the boundary circle.

Yasha 2012-06-26 21:17:11
Can we narrow things down even more? Is there a particular place we could put p without losing any generality?

Maz906 2012-06-26 21:17:44
(1,0)?

Tonitruant 2012-06-26 21:17:44
(0,1)?

Yasha 2012-06-26 21:17:49
Sure! The disc has rotational symmetry, so we can rotate everything until p = (0,1).

nemarci 2012-06-26 21:17:53
draw a segment between two points of the circle, and search the furthest point of the origin on the segment. It's going to be at the end of the segment

Yasha 2012-06-26 21:17:59
Yeah, we're going to do something like that.

Yasha 2012-06-26 21:18:06

yingted 2012-06-26 21:18:29
r=zp+(1-z)q

Yasha 2012-06-26 21:18:35

Global 2012-06-26 21:18:46
(0(1-t)+xt, 1(1-t)+yt), 0<=t<=1

Yasha 2012-06-26 21:18:54
How can we tell if such a point is within the disc of radius 1 centered at the origin?

CDerwin1 2012-06-26 21:19:35
distance from origin

Maz906 2012-06-26 21:19:35
if the distance between r and the origin is less than 1

Global 2012-06-26 21:19:35
show that (1-t+tx)^2 + (ty)^2 <=1

Yasha 2012-06-26 21:19:47
We can just take the distance squared using coordinates.

Yasha 2012-06-26 21:19:51

Yasha 2012-06-26 21:19:57

Yasha 2012-06-26 21:20:08
And we're done.

Yasha 2012-06-26 21:20:17
(d) Suppose P is a convex quadrilateral. What are the possible P-distances between vertices of P? What about when P is a convex hexagon? (Remember: P must still be centrally symmetric!)

Yasha 2012-06-26 21:20:36
Is there anything special about a centrally symmetric convex quadrilateral?

bobthesmartypants 2012-06-26 21:20:54
parallellogram

AwesomeToad 2012-06-26 21:20:54
it's a parallelogram

yingted 2012-06-26 21:20:58
parallelogram

bobthesmartypants 2012-06-26 21:20:58
paralellogram*

Yasha 2012-06-26 21:21:06
It must be a parallelogram! Given any side, multiplying it by -1 takes it to another side by central symmetry, and that new side is parallel to the original.

Yasha 2012-06-26 21:21:11
That should make things easier. Let's suppose our parallelogram has two adjacent corners p and q, so that its other corners are -p and -q.

Yasha 2012-06-26 21:21:17
What is the P-distance between any corner and its opposite?

Watermelon876 2012-06-26 21:21:26
2

yingted 2012-06-26 21:21:29
2

Yasha 2012-06-26 21:21:34
The p-distance between p and -p or q and -q is always 2, since the length of the diagonal is twice the distance from the origin to the corner.

Yasha 2012-06-26 21:21:40
What is the P-distance between p and q?

Watermelon876 2012-06-26 21:21:53
It turns out to be 2!

yingted 2012-06-26 21:22:02
2

Yasha 2012-06-26 21:22:04
This time, p - q corresponds to the length of the side connecting them, which is twice the length of the segment parallel to that side connecting the center and boundary. So the distance is 2 again.

Yasha 2012-06-26 21:22:11
And of course the P-distance between any vertex and itself is 0. So the possibilities are 0 and 2.

iamawesome123 2012-06-26 21:22:18
2

Yasha 2012-06-26 21:22:19
What happens in the case of a hexagon?

yingted 2012-06-26 21:22:48
2

Watermelon876 2012-06-26 21:22:48
This logic doesn't work as well

bobthesmartypants 2012-06-26 21:22:48
1?

Yasha 2012-06-26 21:22:55
Here's one example of how to do it: take the hexagon with vertices at (0,2), (1,d), (1,-d), (0,-2), (-1,-d), and (-1,d), where 0 < d < 2.

Yasha 2012-06-26 21:23:06
It's easy to show that the P-distance from (1,d) to (1, -d) is d. So we can get anything between 0 and 2 using adjacent vertices.

Yasha 2012-06-26 21:23:13
But we can also get 2 using opposite vertices, as before, and 0 using the distance from a vertex to itself.

Yasha 2012-06-26 21:23:20
However, we haven't shown that it's impossible to get anything higher than 2. Maybe there's some weird hexagon where the P-distance between adjacent vertices is 3. We'll need to use the proof of the next part to show that [0,2] is indeed all that's possible.

Yasha 2012-06-26 21:23:37
(e) Let P be the perimeter of some centrally symmetric convex body, and let (a,b) be a point on P. What is the largest possible P-distance from (a,b) to another point on P? Will (a,b) be at this P-distance from just one other point on P or from multiple other points? (If any of your answers depend on the geometry of P and/or on the choice of (a,b), explain how.)

Yasha 2012-06-26 21:23:58
Given what we've tried so far, we might suspect the answer is 2.

Yasha 2012-06-26 21:24:04
Is there definitely another point q on P such that the P-distance between p = (a,b) and q is 2?

Watermelon876 2012-06-26 21:24:59
It can be as large as we want it do if we construct a hexagon with vertices (-1,1) (0,2a) (a,a) and the reflections

Yasha 2012-06-26 21:25:01
That might not be convex for all a.

nemarci 2012-06-26 21:25:12
mirrored to the center of P

yingted 2012-06-26 21:25:12
there is one, but not guaranteed to be many

Watermelon876 2012-06-26 21:25:12
yes the opposite vvertex

yingted 2012-06-26 21:25:21
antipodal point?

Yasha 2012-06-26 21:25:26
Sure. We'll take q = (-a,-b), which must be on P by central symmetry. That gives us a P-distance of 2 between p and q.

Yasha 2012-06-26 21:25:32
Now, we want to prove that no greater distance is possible. Let's take an arbitrary p and q. We want to show the P-distance is less than or equal to 2. That means that the ray in the direction p - q intersects P at a point whose distance from the origin is at least 1/2 the length of p - q.

Yasha 2012-06-26 21:25:46
In other words, we want to show that the point 1/2 (p - q) is on or inside P. How can we do that?

yingted 2012-06-26 21:26:38
go to origin and back

Yasha 2012-06-26 21:26:41
You might be assuming the triangle inequality, which we haven't actually proved for P-distances!

Yasha 2012-06-26 21:27:10
But we can show that 1/2(p-q) is on or inside P from more basic principles.

Yasha 2012-06-26 21:27:23
Ideas?

Yasha 2012-06-26 21:27:46
We'll use symmetry first. Since q is on P, -q is on P. Then what?

Yasha 2012-06-26 21:28:34
So, p is on P, and -q is on P. What can we say about (p-q)/2?

Yasha 2012-06-26 21:29:05
Geometrically, how does the point (p-q)/2 relate to p and -q?

yingted 2012-06-26 21:29:17
midpoint!

yingted 2012-06-26 21:29:22
which is insode

Yasha 2012-06-26 21:29:27
1/2 (p - q) is the midpoint of the segment connecting p and -q. So 1/2 (p - q) is on or inside P, by convexity. Therefore, the ray in the direction p - q intersects P at a point whose distance from the origin is at least as far as 1/2 (p - q), which means the P-distance is at most 2.

Yasha 2012-06-26 21:29:49
Now let's answer the other parts: will (a,b) be P-distance 2 from just one other point, or multiples?

yingted 2012-06-26 21:30:09
can be multiple

Yasha 2012-06-26 21:30:19
Sure, the parallelogram gives us that example.

Yasha 2012-06-26 21:30:32
Could it be just one point?

yingted 2012-06-26 21:30:42
circle

Yasha 2012-06-26 21:30:55
Yeah, on the circle the opposite point is the only point distance two away.

Yasha 2012-06-26 21:31:05
The answer will depend on the geometry of P.

yingted 2012-06-26 21:31:27
you have to project it

yingted 2012-06-26 21:31:27
and find the tangent

yingted 2012-06-26 21:31:27
to get the solution set

Yasha 2012-06-26 21:31:37
For a convex quadrilateral, it's achieved for all other corners. In fact, it's not hard to show, using convexity, that the P-distance remains 2 on any line segment connecting two corners which are both P-distance 2 from the original point.

Yasha 2012-06-26 21:32:03
For general shapes, that is.

Yasha 2012-06-26 21:32:09
(f) In principle, we could define P-distance even when P doesn't come from a convex body and/or is not centrally symmetric. But it turns out that in both of these cases, the definition is problematic: the resulting quantity doesn't behave in the ways we expect a "distance" to behave. Can you determine what problematic issues arise?

Yasha 2012-06-26 21:32:20
First, what happens if we lose central symmetry?

yingted 2012-06-26 21:32:33
you lose actual symmetry

Yasha 2012-06-26 21:32:37
Then the P-distance from x to y is not necessarily the same as the P-distance from y to x, because we're taking the point in the opposite direction! This is bad; we want distance not to depend on order.

Watermelon876 2012-06-26 21:32:50
if it's not centrally symmetric, the distance between two points one way is different than the other way

Yasha 2012-06-26 21:32:52
What happens if we throw out convexity?

yingted 2012-06-26 21:33:02
triangle

Yasha 2012-06-26 21:33:07

Yasha 2012-06-26 21:34:35

bobthesmartypants 2012-06-26 21:34:59
multiple points?

Yasha 2012-06-26 21:35:12
It could be multiple points, but there is one point where we know it must hit P.

yingted 2012-06-26 21:35:25
it is at p

yingted 2012-06-26 21:35:32
but the magnitude is only 1-lambda

ehhhhe 2012-06-26 21:35:35
p

Yasha 2012-06-26 21:35:55

yingted 2012-06-26 21:36:07
lambda

Yasha 2012-06-26 21:36:11

Yasha 2012-06-26 21:36:17

yingted 2012-06-26 21:36:39
more than 1!?!

Yasha 2012-06-26 21:36:46
We don't know, but it must be more than 1, because that point is outside P.

Yasha 2012-06-26 21:36:51
So we've violated the triangle inequality! We can get from the origin to that point with total P-distance equal to 1, if we take an indirect route, but if we go straight there, the distance is greater than 1.

yingted 2012-06-26 21:37:23
the worst, though, is the loss of the "function" part

Yasha 2012-06-26 21:37:40
Well, so if you go by the original definition, I think it's still well-defined.

Yasha 2012-06-26 21:37:56
The original definition asks for the minimum k that puts the second point inside the region, which is still well-defined.

Yasha 2012-06-26 21:38:39
For a non-convex body, as you grow your region, you might eat up the point and then spit it out again and then eat it a third time, but the minimum value of k is still well-defined.

Yasha 2012-06-26 21:38:53
Anyways, onwards to problem 6:

Yasha 2012-06-26 21:38:57
Problem 6: Islands and Bridges.

Yasha 2012-06-26 21:39:01
An ocean has infinitely many islands. Every island is labeled by one of the integers ...,-3,-2,-1,0,1,2,3,..., with no two islands having the same label and every integer being the label of some island. Two islands are connected by a bridge if their labels differ by a power of two. For instance, there is a bridge connecting island 7 and island -25.

Yasha 2012-06-26 21:39:05
We define the distance between two islands k_1 and k_2 to be the minimum number of bridges needed to get from k_1 to k_2. For instance, the distance between the islands 0 and 7 is 2. (You can move from island 0 to island 8, then to island 7; this is the minimum, since you can't go from 0 to 7 using just one bridge.)

Yasha 2012-06-26 21:39:19
First, let's think a bit about this notion of distance. Does it have any nice properties?

Watermelon876 2012-06-26 21:39:49
the distance from x to y is the same as the distance from y to x

yingted 2012-06-26 21:39:49
symmetry?

Yasha 2012-06-26 21:40:05
Sure, since you can go both directions along bridges, there is symmetry.

bobthesmartypants 2012-06-26 21:40:09
you can get from any island to any other one

Yasha 2012-06-26 21:40:39
Yes, that's important, too. Otherwise, the distance could be infinite!

hatchguy 2012-06-26 21:40:59
bridges only join islands with same parity

Yasha 2012-06-26 21:41:01
Not quite, since 1 counts as a power of 2.

Watermelon876 2012-06-26 21:41:09
translation independent

Watermelon876 2012-06-26 21:41:09
the distance between x+n and y+n is the same as the distance between x and y

Yasha 2012-06-26 21:41:17
For one thing, distance is translation invariant. That is, d(x,y) = d(x + c, y + c) for any number c. Any sequence of adding or subtracting powers of two that will take us from x to y will also take us from x + c to y + c.

Yasha 2012-06-26 21:41:25
This means that if we want to find two islands that are distance r from each other, what do we actually need to find?

yingted 2012-06-26 21:41:51
you can erase a variable

Watermelon876 2012-06-26 21:41:51
an island a distance r from 0

Yasha 2012-06-26 21:41:58
It is necessary and sufficient to find an island x such that d(0,x) = r.

MA7HL0V3R 2012-06-26 21:42:10
An island r distance from island 0?

Yasha 2012-06-26 21:42:23
Can anyone think of such an island?

yingted 2012-06-26 21:42:33
basically space out powers

Tonitruant 2012-06-26 21:42:40
Binary number 101010...

Yasha 2012-06-26 21:42:46

Yasha 2012-06-26 21:42:52
(We decided to write all our numbers in binary because the central definition is about powers of two.)

Yasha 2012-06-26 21:43:02
It's certainly obvious that d(0,x) is no more than r. But is it obvious that it's actually equal to r?

Yasha 2012-06-26 21:43:45
The distance is no more than r because the binary expansion gives us the r powers of 2 we need to add to get to x.

Yasha 2012-06-26 21:43:54
It's not obvious that there's no shorter path to get to x from 0, though.

yingted 2012-06-26 21:43:57
use induction

Yasha 2012-06-26 21:44:05
Perhaps surprisingly, proving this one simple fact is the heart of this whole problem! We're going to state it as a stronger lemma, which will make the future parts of the problem easier.

Yasha 2012-06-26 21:44:17

Yasha 2012-06-26 21:44:29

Yasha 2012-06-26 21:44:33
Does anyone see one part of this equality which is straightforward?

Yasha 2012-06-26 21:45:07
It's not hard to see that the distance from 0 to any such x or y must be less than or equal to r, since each of these numbers only has r nonzero digits in binary, which provide a sequence of powers of two to add! So we really only need to show that it's at least r.

Yasha 2012-06-26 21:45:23
As yingted suggests, we can use induction.

Yasha 2012-06-26 21:45:31
The base cases for r = 1 and 2 are easy to check.

Yasha 2012-06-26 21:45:35
Now, let's assume it's true for all values up to r, and try to prove it for r+1.

Yasha 2012-06-26 21:45:42
This next part gets quite complicated, so I encourage you to try to go through it on your own afterwards; it's entirely possible you won't fully understand everything the first time.

Yasha 2012-06-26 21:46:00
In the interests of time, I'll just go through it quickly.

Yasha 2012-06-26 21:46:08

Yasha 2012-06-26 21:46:22

Yasha 2012-06-26 21:46:35

Yasha 2012-06-26 21:46:46
Therefore, d(0,y) = r+1.

Yasha 2012-06-26 21:46:53

Yasha 2012-06-26 21:46:58
But in either case, that gives us that d(0,y) = r + 1 as before.

Yasha 2012-06-26 21:47:03

Yasha 2012-06-26 21:47:11

Yasha 2012-06-26 21:47:16

Yasha 2012-06-26 21:47:22

Yasha 2012-06-26 21:47:27

Yasha 2012-06-26 21:47:34

Yasha 2012-06-26 21:47:38

Yasha 2012-06-26 21:47:43

Yasha 2012-06-26 21:47:48
Again, this was a rather complicated induction proof, so don't panic if you didn't catch all the details. The big picture is what counts: numbers with isolated by 1's, separated by zeroes in their binary expansion, have distance to 0 equal to the number of 1's in the expansion.

Yasha 2012-06-26 21:48:26
I'll pause for a bit to make sure you get this point, and then we'll move forward.

Yasha 2012-06-26 21:48:42

Yasha 2012-06-26 21:48:47
(b) An infinite path in our ocean consists of an infinite set of islands I and an infinite set of bridges B, with each bridge in B joining two islands in the set I, such that:
* every island in I is connected to exactly two bridges in B,
* for any two islands in I, you can get from one to the other using only bridges in B.
Here is one example of an infinite path: let I be the set of all odd-numbered islands and let B be the set of bridges between islands in I whose labels differ by 2. It is easy to see that I and B satisfy both conditions for an infinite path:
* Each island k in I is connected to exactly two bridges in B – namely, the bridges leading to islands k-2 and k+2;
* To get from any odd-numbered island to any other using bridges in B, you start at the smaller number and keep adding 2.
As a warm-up, can you create an infinite path with the same I as in the example above, but with a different B?

Yasha 2012-06-26 21:49:15
Does anyone see a simple way to modify the above example to make a different infinite path with the same set of islands?

Watermelon876 2012-06-26 21:50:11
0 to 4,4 to 2, etc.

Yasha 2012-06-26 21:50:34
Er, odd-numbered islands, but apart from that it's the right strategy.

Yasha 2012-06-26 21:50:43
We can just make one small local change. Here's an example:

Yasha 2012-06-26 21:50:48

Yasha 2012-06-26 21:50:52

Yasha 2012-06-26 21:51:07
Of course, there are lots of other possible examples.

Yasha 2012-06-26 21:51:12
(c) Is it possible to construct an infinite path in our ocean such that, for any two islands k_1, k_2 in I, the minimum number of bridges in B needed to get from k_1 to k_2 is exactly the distance between k_1 and k_2? For instance, the infinite path in our example does not have this property: it takes two bridges in B to go from island 1 to island 5 (you have to go via island 3), even though the distance between these two islands is 1 (there is a single bridge not in B that connects them to each other). If your answer is yes, give an example of sets I and B that work. If your answer is no, prove that it can't be done.

Yasha 2012-06-26 21:51:53
We'll make heavy use of the lemma we proved earlier.

Yasha 2012-06-26 21:52:02

Yasha 2012-06-26 21:52:13
If we subtract any two of these, we get a number with no consecutive ones, so it's easy to see that the minimum number of bridges is in fact the distance.

Yasha 2012-06-26 21:52:21
How can we extend this chain to be infinite in both directions?

nemarci 2012-06-26 21:53:05
-100, -1000100, ...

MA7HL0V3R 2012-06-26 21:53:08
0, 100, 1000100, 10001000100, etc.

Yasha 2012-06-26 21:53:14
We can just go into the negatives, but placing the ones slightly differently.

Yasha 2012-06-26 21:53:20

Yasha 2012-06-26 21:53:25
A few applications of the lemma will show that this infinite path has the desired properties. (I'll skip them for now in the interest of time.)

Yasha 2012-06-26 21:53:31
(d) Does there exist a set S of 9 islands such that:
* the configuration of bridges connecting pairs of islands in S is exactly as in the picture below (with no additional bridges between any of the islands), and
* the distance between any two islands in S equals the minimum number of bridges needed to get from one island to the other via islands in S?

Yasha 2012-06-26 21:54:00

What if, instead of a 3x3 grid, we had an nxn grid: for which n is such a configuration possible?

Yasha 2012-06-26 21:54:09
We'll dive straight into the nxn version.

yingted 2012-06-26 21:54:13
65,1,5,64,0,4,80,16,20

Yasha 2012-06-26 21:54:28
That looks like it might work for the 3 by 3 case, though I haven't checked it.

Yasha 2012-06-26 21:54:34

Yasha 2012-06-26 21:54:42
The sequences we used in part (c) will help us out here:

yingted 2012-06-26 21:54:59
you must split each row or column

yingted 2012-06-26 21:54:59
in base 4, assign a 1 to one side and 0 to the other side

Yasha 2012-06-26 21:55:11
That sounds somewhat similar to the solution I have,

Yasha 2012-06-26 21:55:15

Yasha 2012-06-26 21:55:19

Yasha 2012-06-26 21:55:23

Yasha 2012-06-26 21:55:28
Checking that the distances are correct uses similar logic to part (c), including the lemma from part (a).

Yasha 2012-06-26 21:55:39

Yasha 2012-06-26 21:55:44

Yasha 2012-06-26 21:55:49
Again, we'll skip the the other cases in the interest of time.

Yasha 2012-06-26 21:56:00
(e) Suppose, in a sea far away, we have islands labeled in the same way, with two islands connected by a bridge if their labels differ by a power of 3. Is there a one-to-one correspondence between islands in the ocean and islands in the far-away sea, such that two islands in the ocean are connected by a bridge precisely when the corresponding two islands in the sea are connected by a bridge?

yingted 2012-06-26 21:56:19
no

yingted 2012-06-26 21:56:19
0,1,2

yingted 2012-06-26 21:56:19
use parity

Yasha 2012-06-26 21:56:27
If you start by drawing the appropriate graph of bridges for small integers, you may suspect that there is no such correspondence.

Yasha 2012-06-26 21:56:30
Perhaps surprisingly, there's a way to prove this without any use of the preceding work.

Yasha 2012-06-26 21:56:59
We look for features that our set of islands in the Binary Sea has that the islands in the Ternary Sea might not have.

Yasha 2012-06-26 21:57:11
As yingted mentions, we have a triangle in the Binary sea: 0, 1, 2.

Yasha 2012-06-26 21:57:16
Is it possible for there to be three islands in the Ternary Sea with bridges connecting them?

MA7HL0V3R 2012-06-26 21:57:26
No

Yasha 2012-06-26 21:57:31
No, it isn't! Why not?

yingted 2012-06-26 21:58:03
all powers of 3 are odd

Yasha 2012-06-26 21:58:08
Powers of three are all odd. There's no way to add or subtract three of them and get back to zero, because you'll always get an odd number.

Yasha 2012-06-26 21:58:15
So the answer is no: there is no such correspondence.

Watermelon876 2012-06-26 21:58:37
that's a nice proof

Yasha 2012-06-26 21:58:49
Indeed, it's a neat trick for (e).

nemarci 2012-06-26 21:59:01
there are no a+b=c numbers, where a, b and c are power of 3

Yasha 2012-06-26 21:59:09
Yeah, that's another way of putting it.

Yasha 2012-06-26 21:59:13
OK, onwards to the last problem!

Yasha 2012-06-26 21:59:40
This one has some easier parts at the beginning, which will be refreshing after these tricky problems.

Yasha 2012-06-26 21:59:47
Problem 7: Mentor Pyramids.

Yasha 2012-06-26 21:59:53
Last summer, the graduate students teaching at Mathcamp (we call them "mentors") arranged themselves into a pyramid with four layers:

Yasha 2012-06-26 21:59:58

Watermelon876 2012-06-26 22:00:13
This was my favorite question

Yasha 2012-06-26 22:00:15
Awesome!

Yasha 2012-06-26 22:00:21

Yasha 2012-06-26 22:00:31

Yasha 2012-06-26 22:00:42
(a) Find the weight supported by the mentor at the bottom left corner of a pyramid with n layers.

Yasha 2012-06-26 22:00:53
The weight that someone supports does not depend on what happens below them. Therefore, the first few values for the weight supported by the mentor at the bottom left corner of a pyramid with n layers can be read off of the left side of the example above: 1, 3/2, 7/4, 15/8, etc.

Yasha 2012-06-26 22:01:01
Based on the first few values, what do we think the answer is?

jared429 2012-06-26 22:01:30

yingted 2012-06-26 22:01:30
2-2^(1-n)

nemarci 2012-06-26 22:01:30
2-(1/2)^(n-1)

Yasha 2012-06-26 22:01:36

JonathanLi 2012-06-26 22:01:41
Will the transcript be posted online? if so, where?

Yasha 2012-06-26 22:02:16
Yeah, if you go to the MathJams page, there's a link for archived MathJams. You can see transcripts of old MathJams there, and this one will be there in the next couple days.

Yasha 2012-06-26 22:02:26
Probably by tomorrow.

Yasha 2012-06-26 22:02:43
OK, so we have a guess for the formula for the weight supported by the bottom left mentor.

Yasha 2012-06-26 22:02:49
What is a technique we can use to prove this formula?

yingted 2012-06-26 22:02:58
induction ...

Yasha 2012-06-26 22:03:02
We can use induction. What is our base case?

yingted 2012-06-26 22:03:18
top

Watermelon876 2012-06-26 22:03:18
the top person who supports 1

Yasha 2012-06-26 22:03:22

Yasha 2012-06-26 22:03:28

Yasha 2012-06-26 22:03:43
Let's consider a pyramid with k+1 layers, and let's call the mentor at the bottom left corner Ian. Let's call the mentor right above him Paddy. Here's our picture again:

Yasha 2012-06-26 22:03:49

Yasha 2012-06-26 22:03:56
What is the weight supported by Paddy, in terms of k?

nemarci 2012-06-26 22:04:39
2-1/2^(k-1)

Yasha 2012-06-26 22:04:45

Yasha 2012-06-26 22:04:52
How can we find the weight that Ian supports?

Watermelon876 2012-06-26 22:05:17
1+ 1/2 of the weight Paddy supports

nemarci 2012-06-26 22:05:17
1+1/2*(2-1/2^(k-1))

Yasha 2012-06-26 22:05:22
Ian supports his weight of 1, plus half of the weight supported by the mentors leaning on him, which in this case is just the weight supported by Paddy.

Yasha 2012-06-26 22:05:27

Yasha 2012-06-26 22:05:31
This statement is exactly what we wanted to show, so it completes the induction.

Yasha 2012-06-26 22:05:34

Yasha 2012-06-26 22:05:38
Any questions on this part?

Watermelon876 2012-06-26 22:06:12
I thought n was different so my answers have n instead of n-1

Yasha 2012-06-26 22:06:40
I of course don't remember your particular case, but generally we don't take off points for typos like that.

Yasha 2012-06-26 22:06:58
as long as the math is correct

Yasha 2012-06-26 22:07:06

Yasha 2012-06-26 22:07:20
Let's call the (k+1)-th mentor from the left in the (m+1)-th layer Mo, and let's call the mentor directly above and to the left Susan, and the mentor above and to the right Mathieu. Here's the picture again:

Yasha 2012-06-26 22:07:26

Yasha 2012-06-26 22:07:34
What layer is Susan in, and how far is she from the left?

nemarci 2012-06-26 22:08:25
mth layer, kth from left

Yasha 2012-06-26 22:08:31
Susan is in the mth layer. Counting carefully, we see that she is the kth mentor from the left in that layer. What about Mathieu?

Watermelon876 2012-06-26 22:08:57
mth layer k+1 th from left

nemarci 2012-06-26 22:08:57
mth layer, (k+1)-th from left

Yasha 2012-06-26 22:09:03
Mathieu is in the mth layer and is the (k+1)-th mentor from the left.

Yasha 2012-06-26 22:09:07
In terms of W, what is the weight supported by Susan?

Watermelon876 2012-06-26 22:09:30
W(k-1,m-1)

Yasha 2012-06-26 22:09:35
By definition, the weight supported by Susan is W(k-1,m-1). What about the weight supported by Mathieu?

Watermelon876 2012-06-26 22:09:41
W(k,m-1)

Yasha 2012-06-26 22:09:47
By definition, the weight supported by Mathieu is W(k,m-1).

Yasha 2012-06-26 22:09:50
What is the weight supported by Mo?

yingted 2012-06-26 22:09:57
1+(left+right)/2

nemarci 2012-06-26 22:10:03
W(k,m)=1+1/2(W(k-1,m-1)+W(k,m-1))

Yasha 2012-06-26 22:10:10
By the definition of W, it is W(k,m). But, by the problem statement, the weight supported by Mo is equal to his weight plus half of the weight supported by Susan and half of the weight supported by Mathieu.

Yasha 2012-06-26 22:10:18

Yasha 2012-06-26 22:10:24
There's a slight issue, though. Can anyone see it?

Watermelon876 2012-06-26 22:10:41
But wait! What if susan doesn't exist because mathew's the leftmost?

yingted 2012-06-26 22:10:41
base cases

nemarci 2012-06-26 22:10:41
k=0

MA7HL0V3R 2012-06-26 22:10:41
The camper could be on the edge

jared429 2012-06-26 22:10:48
not defined for W(0,0)

ychen428 2012-06-26 22:10:55
First case

Yasha 2012-06-26 22:11:01
There is a problem with the mentors on the edges of the pyramid. They only have one mentor above them, so the formula doesn't quite make sense.

Yasha 2012-06-26 22:11:06

Yasha 2012-06-26 22:11:25
W(-1,m-1) represents the weight supported by the 0th mentor from the left in the mth row, which doesn't make sense. W(m,m-1) represents the weight supported by the (m+1)-th mentor in the mth row, which also doesn't make sense.

Yasha 2012-06-26 22:11:30
What should we do?

Watermelon876 2012-06-26 22:11:43
but wait! we have a formula for mentors on the edge!

Yasha 2012-06-26 22:11:46
We can do that, but there's something simpler we can do.

yingted 2012-06-26 22:11:58
basically, let everything else =0

nemarci 2012-06-26 22:11:58
their weights should be 0

yingted 2012-06-26 22:11:58
let the air =0

Yasha 2012-06-26 22:12:03
We can set W(k,m) to zero whenever it is out of the range of the pyramid. Doing this will make our recursive formula for W still correct even when we look at W(0,m) and W(m,m).

Yasha 2012-06-26 22:12:23
What values of k and m correspond to actual mentors in the pyramid?

yingted 2012-06-26 22:12:51
k is between 0 and m

nemarci 2012-06-26 22:12:57
0<=k<=m

Yasha 2012-06-26 22:13:00

Yasha 2012-06-26 22:13:08

Yasha 2012-06-26 22:13:15

Yasha 2012-06-26 22:13:23
Any questions on this part?

jared429 2012-06-26 22:13:53
what exactly is the final solution?

Yasha 2012-06-26 22:14:22

Yasha 2012-06-26 22:14:31
Otherwise, W(k,m)=0.

Yasha 2012-06-26 22:15:11
Onwards!

Yasha 2012-06-26 22:15:16

Yasha 2012-06-26 22:15:34
What's a technique that might be helpful for this problem?

Maz906 2012-06-26 22:15:51
generating functions?

Yasha 2012-06-26 22:16:01
There is a solution with generating functions, but I won't go through that one here.

Watermelon876 2012-06-26 22:16:17
Solving part d first and then looking at part c

Yasha 2012-06-26 22:16:34
It's unclear if there's a closed form for general W(k,m) actually. There is one in this special case, though.

nemarci 2012-06-26 22:16:50
induction

Yasha 2012-06-26 22:16:57
We could try induction. That is, we could try to find W(n,2n) in terms of W(n-1,2(n-1)).

Yasha 2012-06-26 22:17:21
It's not immediately clear how to get induction to work, but here's a picture that hints at one possible method:

Yasha 2012-06-26 22:17:27

BarbieRocks 2012-06-26 22:18:24
i experimented and found a summation that worked for (d), proved it by induction, then proved a hard identity to make (c) simpler

Yasha 2012-06-26 22:18:27
Yes, you can certainly find a summation formula for (d) and then try to sum it in part (c). We won't go that route though.

Yasha 2012-06-26 22:18:43
Anyways, the picture describes trying to compute W(3,6), which is the weight supported by the circled mentor.

Yasha 2012-06-26 22:18:50
Let's call the circled mentor Mo.

Yasha 2012-06-26 22:18:55
We're going to work with the special case n=3 for a while, and then we will see how we can generalize our method.

Yasha 2012-06-26 22:19:00
One way to compute the weight supported by Mo is to add up the contributions to that weight from all of the mentors in the pyramid (including Mo himself).

Yasha 2012-06-26 22:19:13
What can you say about the weight contributed by the mentors in the gray regions to the weight that Mo supports?

nemarci 2012-06-26 22:19:40
0

Maz906 2012-06-26 22:19:40
no contribution

yingted 2012-06-26 22:19:40
none?

Yasha 2012-06-26 22:19:46
There is no downward path from the mentors in the gray regions to Mo, so Mo does not support any of their weight. The only mentors whose weights matter are the ones in the diamond-shaped non-gray region.

yingted 2012-06-26 22:19:56
wait, a closed-form summation for (d)? no hypergeometric pFq functions?

Yasha 2012-06-26 22:20:23
Er, as in you can find a formula that involves a sum, but as far as I know you can't evaluate the sum to find a closed form solution.

Yasha 2012-06-26 22:20:28
For part (d), that is.

Yasha 2012-06-26 22:20:49
For part (c), we will find a closed form solution, as the problem asks.

Yasha 2012-06-26 22:21:01
Anyways, I think the picture might have floated all the way up, so I will repost it.

Yasha 2012-06-26 22:21:05

Yasha 2012-06-26 22:21:20
As we saw, we can ignore the gray vertices.

Yasha 2012-06-26 22:21:26
What can we say about the total weight contributed by the mentors in the black region?

Watermelon876 2012-06-26 22:21:56
equal to W(k-1, 2k-2)

yingted 2012-06-26 22:22:03
we can use induction

Maz906 2012-06-26 22:22:03
W(n-1, 2(n-1)

Yasha 2012-06-26 22:22:11
The mentors in the black region form a smaller diamond, which can be viewed as part of a smaller pyramid where Mo is in the middle of the fourth row.

Yasha 2012-06-26 22:22:17
Therefore, the weight contributed by the mentors in the black region is W(2,4).

Yasha 2012-06-26 22:22:41
When we do the general case, it will be W(n-1,2(n-1)), as people suggest.

Yasha 2012-06-26 22:22:47
OK, so now all we have to do is figure out the weights contributed by the mentors in the blue and red regions. (We will think of the top mentor as being both blue and red, and hence colored purple.)

Yasha 2012-06-26 22:22:56
As an example, let's pick one of the blue mentors and call her Quirk, and figure out how much weight Quirk contributes to the weight that Mo supports.

Yasha 2012-06-26 22:23:00

Yasha 2012-06-26 22:23:06
Let's say Quirk is the circled blue mentor, and let's consider downward paths from Quirk to Mo.

Yasha 2012-06-26 22:23:17

Yasha 2012-06-26 22:23:22
How many such downward paths are there from Quirk to Mo?

yingted 2012-06-26 22:23:42
5C2=5C3?

nemarci 2012-06-26 22:23:42
10

Yasha 2012-06-26 22:23:52

Yasha 2012-06-26 22:24:07
Given a particular path, how much of Quirk's weight "flows" along that path to Mo?

yingted 2012-06-26 22:24:25
2^-5

Maz906 2012-06-26 22:24:25
1/32=1/(2^5)

Yasha 2012-06-26 22:24:31

Yasha 2012-06-26 22:24:35
What then is the total weight that Quirk contributes to the weight supported by Mo?

Maz906 2012-06-26 22:24:54
ncr(5, 2)*1/(2^5)

nemarci 2012-06-26 22:24:54
10/32

Maz906 2012-06-26 22:24:54
10/32 = 5/16

yingted 2012-06-26 22:24:54
multiply them

Yasha 2012-06-26 22:24:59

Yasha 2012-06-26 22:25:04
What about the top mentor? How much weight does the top mentor contribute to Mo?

Watermelon876 2012-06-26 22:25:43
6 choose 3 times 2^{-6}

yingted 2012-06-26 22:25:48
6C3 2^-6

nemarci 2012-06-26 22:25:49
6C3/2^6=20/64=5/16

Yasha 2012-06-26 22:25:54

Yasha 2012-06-26 22:25:58
What about the blue mentor in the third row?

Yasha 2012-06-26 22:26:24
(Third from the top, that is, so in position (0,2).)

yingted 2012-06-26 22:26:55
4C1 2^-4

Maz906 2012-06-26 22:26:55
4/16=1/4

nemarci 2012-06-26 22:26:55
4C3/2^4=1/4

Yasha 2012-06-26 22:27:00

Yasha 2012-06-26 22:27:07
And the blue mentor in the fourth row?

yingted 2012-06-26 22:27:25
3C0 2^-3

Yasha 2012-06-26 22:27:31

nemarci 2012-06-26 22:27:41
1/8

Yasha 2012-06-26 22:27:48
What is the total contribution of the mentors in the blue region to the weight supported by Mo? (Remember that the top purple mentor counts as both blue and red.)

nemarci 2012-06-26 22:28:13
1

Yasha 2012-06-26 22:28:18

Yasha 2012-06-26 22:28:25
Therefore, the total weight contributed by the mentors in the red region is also 1.

Yasha 2012-06-26 22:28:34
What, then, is a recursive formula for W(3,6) in terms of W(2,4)?

Yasha 2012-06-26 22:29:35
It's tempting to add up the contributions from the black, blue, red regions. However, W(3,6) is not equal to W(2,4)+2. What is the problem?

nemarci 2012-06-26 22:29:55
we counted the top person twice

yingted 2012-06-26 22:30:05
overcounting?

Maz906 2012-06-26 22:30:05
overcounted the top most mentor - two times

Yasha 2012-06-26 22:30:07
We've double-counted the weight contributed by the purple mentor, since the purple mentor is both in the blue region and in the red region. What then is the correct formula for W(3,6) in terms of W(2,4)?

Maz906 2012-06-26 22:30:56
W(3,6)=W(2,4) + 27/16

nemarci 2012-06-26 22:30:56
W(3,6)=W(2,4)+2-6C3/2^6

Yasha 2012-06-26 22:31:01

Yasha 2012-06-26 22:31:06
In the case where n=3, the sum of the contributions from the blue region turned out to be exactly one. Assuming that this wasn't just a coincidence, what is the correct generalization of the above formula to a general n?

bluepie 2012-06-26 22:32:24
what is this class about?

Yasha 2012-06-26 22:32:26
We're going over the solutions of the Mathcamp qualifying quiz, available at http://www.mathcamp.org/prospectiveapplicants/quiz/index.php

nemarci 2012-06-26 22:32:33
W(n,2n)=W(n-1,2(n-1))+2-2nCn/2^(2n)

Yasha 2012-06-26 22:32:45
For a general n, we can split up the pyramid into gray, black, blue, and red regions analogously.

Yasha 2012-06-26 22:32:49
As before, the contribution of the gray region is zero and the contribution of the black region is W(n-1,2(n-1)).

Yasha 2012-06-26 22:32:52
We're assuming for now that the blue and red regions each contribute a weight of 1. (I'm leaving the proof of this fact for later.)

Yasha 2012-06-26 22:32:56

Yasha 2012-06-26 22:33:06

Yasha 2012-06-26 22:33:13

Yasha 2012-06-26 22:33:23
It's not immediately obvious how to compute this sum.

Yasha 2012-06-26 22:33:38
There are a couple approaches to tackling it. A natural thing to try first is to multiply through by 2^(2n) to get rid of the fractions, and then compute some of the first few values of the series.

Yasha 2012-06-26 22:33:43
The result is 1, 6, 30, 140, 630, 2772, 12012, 51480, and so forth.

Yasha 2012-06-26 22:33:52
Since you're allowed to use the internet, one thing to do after that is to try to find the sequence in the online encyclopedia of integer sequences at http://oeis.org/

Yasha 2012-06-26 22:34:26
You'll find it there, but of course you still have to prove it.

Yasha 2012-06-26 22:34:32
Without the internet, you could try to find a pattern. For example, if you try factoring, you might notice that this sequence is evenly divisible by the sequence 1, 3, 5, 7, 9, 11, 13, 15, etc. Dividing through, we get the sequence 1, 2, 6, 20, 70, 252, 924, 3432. If you look at Pascal's triangle, you'll notice that these numbers appear in the middle of the even-numbered rows.

yingted 2012-06-26 22:34:37
lol

Yasha 2012-06-26 22:34:49
You might also instead try dividing by the sequence 1, 2, 3, 4, 5, 6, 7, 8, etc. It turns out that you'd also find yourself with entries of Pascal's triangle.

Yasha 2012-06-26 22:35:01

ychen428 2012-06-26 22:35:19
WE COULD USE OEIS????

Yasha 2012-06-26 22:35:21
The quiz says that you're allowed to use the internet :)

Yasha 2012-06-26 22:35:29
Of course, finding it in OEIS is not enough.

Yasha 2012-06-26 22:35:47
OEIS will give you a formula that matches the first few terms, but you still have to prove that that formula works for all n.

ychen428 2012-06-26 22:35:59
oh okay :D

Yasha 2012-06-26 22:36:22
OK, so as I said, a guess for the formula is not good enough.

Yasha 2012-06-26 22:36:29
We need proof.

Yasha 2012-06-26 22:36:30

Yasha 2012-06-26 22:36:50
How can we prove this?

melikababadi 2012-06-26 22:37:08
induction

AwesomeToad 2012-06-26 22:37:08
induction?

yingted 2012-06-26 22:37:08
combinatorics or induction

Yasha 2012-06-26 22:37:16
Yes, induction seems like a good bet.

Yasha 2012-06-26 22:37:28
There might be a combinatorial way, but it would be quite tricky to come up with it.

Yasha 2012-06-26 22:37:33

Yasha 2012-06-26 22:37:40
Now we assume that the statement is true for n=m-1, and we'd like to prove it for n=m.

Yasha 2012-06-26 22:37:44

Yasha 2012-06-26 22:37:55

Yasha 2012-06-26 22:37:58
What now?

Yasha 2012-06-26 22:38:37
What can we do to the right hand side to start simplifying?

Yasha 2012-06-26 22:39:18
So, we have the inductive hypothesis to work with.

Yasha 2012-06-26 22:39:20

Yasha 2012-06-26 22:39:28
What can we do next?

Yasha 2012-06-26 22:40:13

yingted 2012-06-26 22:41:04
expand part of it

AwesomeToad 2012-06-26 22:41:04
bash

Yasha 2012-06-26 22:41:13
I'd rather do the opposite of expanding :)

Yasha 2012-06-26 22:41:31

Yasha 2012-06-26 22:41:45
What's something else we can do to get our expression looking more like what we want?

Maz906 2012-06-26 22:42:52
rewrite (2m-1)!/(m-1)!^2 as m*(2m-1)C(m-1)

Yasha 2012-06-26 22:42:59
Sure, that's one thing we could try.

Yasha 2012-06-26 22:43:05
But I want to keep our goal in mind.

Yasha 2012-06-26 22:43:41

Yasha 2012-06-26 22:43:49
We already have the 2^(2m) part.

Yasha 2012-06-26 22:43:56
Let's get the m!^2 part.

Yasha 2012-06-26 22:44:12

Yasha 2012-06-26 22:44:25
What can we do next?

Yasha 2012-06-26 22:44:56

Yasha 2012-06-26 22:45:13

Maz906 2012-06-26 22:45:38
4m^2(2m-1)! = 2m*(2m)!

Yasha 2012-06-26 22:45:48
Yup, that's another way to get to (2m+1)! in the numerator.

Yasha 2012-06-26 22:46:12
A good trick for proving that one expression is equal to another is taking out factors from one expression to make it line up with the other one.

Yasha 2012-06-26 22:46:18

Yasha 2012-06-26 22:46:24
What, then, is W(n,2n)?

Yasha 2012-06-26 22:47:30
I guess our expression for W(n,2n) floated quite a ways up.

Yasha 2012-06-26 22:47:46
Here's that line again:

Yasha 2012-06-26 22:47:48

Yasha 2012-06-26 22:48:00
So, now we substitute.

Yasha 2012-06-26 22:48:01

yingted 2012-06-26 22:48:10
beautiful

Yasha 2012-06-26 22:48:12
There are, of course, lots of equivalent expressions.

Yasha 2012-06-26 22:48:16
Are we done?

Yasha 2012-06-26 22:48:56
There was something I slipped under the rug on our way here.

Maz906 2012-06-26 22:49:18
that the sum of each blue/red region was 1?

Yasha 2012-06-26 22:49:26
Exactly, we used the fact that the weight contributed by the mentors in the blue regions sums to exactly one, and we postponed the proof until later.

Yasha 2012-06-26 22:49:52
In the interests of time, I'm just going to paste in the calculation, but let's set things up first.

Yasha 2012-06-26 22:49:54
Looking back on our example with n=3 to guide us, what is the contribution of the blue (leftmost) mentor in the (k+1)-th row to W(n,2n)?

Yasha 2012-06-26 22:50:46

Yasha 2012-06-26 22:50:52

Yasha 2012-06-26 22:50:57

Yasha 2012-06-26 22:51:02
We would like to show that when we sum this expression over k, we get 1.

Yasha 2012-06-26 22:51:08

Yasha 2012-06-26 22:51:13
In the interests of time, I'm just going to paste in the proof. You can look at it later or try to come up with it on your own.

Yasha 2012-06-26 22:51:17
We proceed by induction. The base case n=0 is easy.

Yasha 2012-06-26 22:51:22

Yasha 2012-06-26 22:51:27

yingted 2012-06-26 22:51:41
this is that proof?

yingted 2012-06-26 22:51:41
no it isn't...

Yasha 2012-06-26 22:52:01
Yup, this proves that the weights contributed by the mentors in the blue region sum to 1.

Yasha 2012-06-26 22:52:18
Anyways, with that, we're done!

Yasha 2012-06-26 22:52:38
Thank you all for coming, particularly those who stuck through all the way to the end.

Yasha 2012-06-26 22:52:51
I'm looking forward to meeting many of you at camp or elsewhere!

Canada/USA MathCamp Qualifying Quiz

Facilitator: Yasha Berchenko-Kogan