MATHCOUNTS Problem Discussion Hour
Go back to the Math Jam ArchiveFormer National MATHCOUNTS test champion Mathew Crawford will assist students in understanding solutions to challenging MATHCOUNTS problems.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Mathew Crawford
Mr.Ocax (19:21:25)
If two positive integers m and n satisfy 1/m+1/n=1/15, then what is the least m+n could be?
Mr.Ocax (19:21:40)
something like that of course, i'd also like to know how to do all problems in that format
MCrawford (19:29:12)
Our first problem is a number theory problem.
MCrawford (19:29:18)
What is difficult about this problem?
RC-7th_? (19:29:31)
Fractions
Monkey (19:29:37)
There are two variables, but only one equation.
MCrawford (19:29:51)
How might we begin dealing with these difficulties?
NoSoupForYou (19:29:59)
multiply by mn
sam3.14 (19:30:02)
multiply by common denom
RC-7th_? (19:30:03)
multiply through by mn?
MCrawford (19:30:40)
I would go one step farther and multiply by 15mn to clear all the denominators.
solafidefarms (19:30:38)
The common denominator is 15mn
MCrawford (19:30:55)
What do we get when we multiply out the denominators?
RC-7th_? (19:31:06)
15m+15n=mn
Mr.Ocax (19:31:09)
so 15(n+m)=mn?
NoSoupForYou (19:31:11)
15(m+n)=mn
oneal3691 (19:31:15)
15n+15m=mn
MCrawford (19:31:30)
Now we have an equation that looks easier to work with, but it still involves two variables.
MCrawford (19:31:38)
What could we do at this point?
solafidefarms (19:31:46)
factor?
MCrawford (19:32:05)
How could we factor?
RC-7th_? (19:32:08)
Move them over, and simon's favorite factoring trick?
Mr.Ocax (19:31:33)
(m-15)(n-15)=-225?
Mr.Ocax (19:31:45)
woops that's a 225
MCrawford (19:32:39)
We first stick everything on one side:
MCrawford (19:32:44)
mn - 15m - 15n = 0.
Mr.Ocax (19:32:34)
whats simon's fav factoring trick? i've heard all about it
Mr.Ocax (19:32:17)
add 225 to both sides?
MCrawford (19:33:09)
I suggest doing a search for it on the forums -- you'll see many great and insightful examples.
MCrawford (19:33:16)
But we'll finish this problem using it.
NoSoupForYou (19:33:13)
who's simon
MCrawford (19:33:31)
ComplexZeta on AoPS -- a great student of mathematics.
solafidefarms (19:33:10)
mn-m-n-1=0=> (m-1)(n-1)=0
MCrawford (19:34:06)
Simon's favorite factoring trick reminds us that we can take a product along with a linear combination of two variables and create a factorization.
MCrawford (19:34:17)
mn + m + n + 1 = (m + 1)(n + 1) for instance
MCrawford (19:34:32)
Here we want something in the form
MCrawford (19:34:39)
(m - something)(n - something)
MCrawford (19:34:55)
Clearly each "something" must be 15 in this case so that we get
MCrawford (19:35:04)
mn - 15m - 15n as part of our expression.
MCrawford (19:35:13)
But, we must do something to our equation.
Monkey (19:34:23)
For the sum of m and n to be as small as possible, then m-15 and n-15 have to be as close as possible to each other, and still multiply to 225.
solafidefarms (19:35:03)
(m-15)(n-15)=225
MCrawford (19:35:31)
We had to add 225, the product (-15)(-15)
Mr.Ocax (19:34:35)
ok i found it on the forum, very helpful
Mr.Ocax (19:31:56)
ahh.. and then use the factors of 225 to find m and n, ok
MCrawford (19:35:44)
Exactly!
MCrawford (19:36:01)
We manipulated our single equation into a form that allows us to apply what we know about integers.
MCrawford (19:36:11)
Hence the number theory aspect of the problem.
uclabb (19:29:29)
60
Mr.Ocax (19:33:02)
so would the answer be 60?
Monkey (19:35:44)
Thus, m and n are each 30, so the sum of them is 60
MCrawford (19:36:33)
How do we know these give us the smallest possible?
RC-7th_? (19:36:09)
Notice that this tells us that (m,n)=(0,0) is okay, but it obviously isn't
MCrawford (19:37:13)
Right -- we need positive integers.
Monkey (19:37:23)
Because they give 15x15=225 in our nice factored equation, and 15 and 15 are as close as possible to each other.
oneal3691 (19:37:23)
can m and n be the same?
MCrawford (19:37:51)
Unless it says "distinct integers", yes, they can be the same.
conartist (19:37:49)
because the extreme factors are larger than those that are closer together: if we have 225 and 1, then our sums are greater than if we have 15 and 15
uclabb (19:38:13)
just like for ab= 64. The lowest a + b can be is 16 (8 + 8)
sam3.14 (19:37:06)
if mn=k, then m+n is minimized when m is closest to n
MCrawford (19:38:38)
Why does this work?
RC-7th_? (19:38:51)
It's based on (a+b)(a-b)=a^2-b^2
MCrawford (19:39:06)
That's one way to do it.
MCrawford (19:39:29)
If the sum of two numbers is 2a, then the largest product is made by setting b equal to 0.
MCrawford (19:39:32)
Conversely...
MCrawford (19:40:17)
A higher sum could always make a higher product, so we still want a + b and a - b to be as close together as possible.
Monkey (19:39:22)
I'm not sure, but it might also work because of the AM-GM inequality.
MCrawford (19:40:36)
For those of you who are familiar with inequalities, this is another good solution.
MCrawford (19:40:57)
The arithmetic mean of a group of nonnegative real numbers is at least as large as their geometric mean.
MCrawford (19:41:10)
The only time equality occurs is when all variables are set equal.
ln(dx/dy)_2 (19:40:50)
What does AM-GM stand for?
MCrawford (19:41:25)
arithmetic mean-geometric mean inequality.
sam3.14 (19:40:43)
Ooh. We can do this with rectangle areas. If the area of a rectangle is fixed, then a square has the smallest perimeter
MCrawford (19:41:51)
True -- and we can use variables just like RC-7th did to make this leap to the geometric analogy!
oneal3691 (19:39:03)
think of it as squares and rectangles and the area of them
NoSoupForYou (19:38:47)
If 1/m+1/n=1/a, would m=a/2 and b/2 always give the greatest possible value for (m + n)?
MCrawford (19:42:23)
I think you mean m = 2a nd n = 2a.
NoSoupForYou (19:42:36)
yeah
MCrawford (19:42:44)
And yes, if you work out the algebra, so long as a is an integer, this will work out.
Mr.Ocax (19:43:03)
what if the number on top of a is a number other than 1?
Mr.Ocax (19:23:34)
Given the equation 1/m+1/n=2/15, where m and n are positive integers, find the value of m+n such that m>n and m is not a mulitple of n.
MCrawford (19:43:27)
Then you're back to working with Simon's favorite factoring trick.
MCrawford (19:43:40)
Let's take a brief review of the most important problem solving concepts here.
MCrawford (19:43:50)
First, we identified the difficulties with the given equation.
MCrawford (19:44:12)
This is extremely important in problem solving as it often gives us a clue as to what steps or tools we might apply.
MCrawford (19:44:33)
Identifying the fractions as a difficulty immediately helps us as we can multiply them away and see if that works:
solafidefarms (19:43:40)
15m+15n=2mn...
MCrawford (19:45:07)
Simon's favorite factoring trick might be a little harder to provoke here because the factorization is going to be harder to create.
Monkey (19:44:52)
Then get all the stuff to one side and factor again...
Mr.Ocax (19:45:03)
and divide by 2 to make factoring easier?
RC-7th_? (19:45:11)
56.25=2(m-7.5)(n-7.5)=>225=2(2m-15)(2n-15)
MCrawford (19:45:44)
Great work. So, what are the possible integers m and n?
kostya (19:45:42)
fractions is what you get
MCrawford (19:45:56)
How do you mean?
kostya (19:46:34)
I mean that if you divide by 2, you'l get fractoins for some time
MCrawford (19:46:52)
So there are no integer solutions.
Mr.Ocax (19:46:58)
they are each 15 aren't they?
MCrawford (19:47:10)
Hmmm, you're right -- where did we go wrong?
MCrawford (19:47:26)
I see the problem.
MCrawford (19:47:41)
RC-7th needed to add 2 * 56.25 to both sides.
MCrawford (19:48:04)
So we should have had 225 = (2m - 15)(2n-15)
MCrawford (19:48:09)
Sorry, I missed that.
Mr.Ocax (19:47:57)
my factorization was (m-7.5)(n-7.5)=56.25
MCrawford (19:48:27)
Yes, that multiplied by 4 gives the right idea.
Mr.Ocax (19:48:24)
so the next closest is m-15/2=45/2 and n-15/2=5/2, so m=30 and n=10
MCrawford (19:49:30)
Hmmm, 25*9 = 225
MCrawford (19:49:37)
I think this makes closer factors.
MCrawford (19:49:45)
But we should move on so that we can look at other problems.
uclabb (19:46:08)
What is the probability that a factor of 15^40 is a multiple of 15^25?
Farazy (19:48:39)
Wouldn't Greedy's Algorithm be quicker?
Farazy (19:49:44)
Greedy's algorithm says find the highest fraction with one in the numerator and subtract from what you want as your result.
MCrawford (19:50:02)
We'll work uclabb's problem.
MCrawford (19:50:17)
How can we examine this problem?
uberl33tmage (19:50:22)
We have 41*41 factors iin 15^40
Monkey (19:50:28)
First factor 15^40 into primes.
sam3.14 (19:50:42)
we should do the prime factorization of each number, I think
MCrawford (19:51:05)
We use prime factorization to organize information about integers.
MCrawford (19:51:19)
It is extremely important not to view this as a formulaic process.
MCrawford (19:51:36)
What must the prime factorization of 15^40 look like?
Farazy (19:51:50)
3^40*5^40
Monkey (19:51:51)
3^40x5^40
solafidefarms (19:51:51)
3^40 5^40
MCrawford (19:52:16)
Sorry, I meant to ask, "what must the prime factorization of a divisor of 15^40 look like?"
NoSoupForYou (19:52:31)
3^a*5^b
Monkey (19:52:38)
3^nx5^m
solafidefarms (19:52:40)
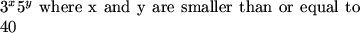
sam3.14 (19:52:43)
3^n 5^m , m,n <= 40
MCrawford (19:52:54)
Each exponent can be from 0 to 40.
MCrawford (19:53:04)
That's why we get 41*41 total divisors.
MCrawford (19:53:10)
Now what?
RC-7th_? (19:50:25)
Find the total number of factors, and find which are multiples
uberl33tmage (19:52:50)
3^(x>or= to 25) *5^(y>or=to 25)
Mr.Ocax (19:53:15)
but because you want a multiple of 15^25,the exponents have to be larger
MCrawford (19:53:38)
*at least as large as 25, but no larger than 40.
RC-7th_? (19:53:36)
16*16 are the number of divisors which are also mulitples
oneal3691 (19:51:00)
so we have 41^2 factors in the first
Monkey (19:53:08)
Which means there are 1681 factors.
uberl33tmage (19:53:47)
there are 16 integes between 25 and 40 inclusive. we have 16*16 successes out of 41*41 total, so our chances are 256/1681
uclabb (19:53:50)
41^2 = 1681, the denominater
uberl33tmage (19:51:33)
there are 16 factors for 3 and 5, As long as the power is more than or equal to 25, we have a success. The probability is (16/41)^2
MCrawford (19:54:21)
That is indeed the probability that a divisor of 15^40 is a multiple of 15^25.
MCrawford (19:54:45)
Remember, in hard divisor problems, prime factorization provides you with the organization for the information that you need.
MCrawford (19:55:02)
If you view divisor problems this way, they often turn into much simpler counting problems.
MCrawford (19:55:17)
Let's look at a geometry problem next.
E^(pi*i)=-1 (19:49:52)
A sphere is inscribed in a cube with side length 9 inches. Then, a smaller cube is inscribed in the sphere. How many cubic inches are in the volume of the inscibed cube?
MCrawford (19:55:34)
What do we need to do with this one?
Mr.Ocax (19:55:35)
make this a 2d problem
MCrawford (19:55:46)
That could help.
MCrawford (19:56:00)
But I think that might actually make this problem harder to think about.
MCrawford (19:56:06)
For a specific reason.
MCrawford (19:56:14)
(but it's often a good idea with 3-D problems)
oneal3691 (19:56:05)
the diameter of the sphere would be 9
Monkey (19:55:59)
Find the radius of the sphere first (which is easy).
Scrambled (19:55:54)
establish sides in terms of the largest radius
oneal3691 (19:56:13)
which would be the space diagonal of the cube
uberl33tmage (19:56:04)
The space diagonal of the smaller cube is equal to a side of the big cube.
oneal3691 (19:56:18)
or 9/rt(3)
Monkey (19:56:23)
Because a radius of the sphere is the space diagonal of the inner cube.
sam3.14 (19:56:23)
the internal diagonal of the smaller square is equal to the diameter of the sphere
uberl33tmage (19:56:41)
the ratio is 1 to root 3
MCrawford (19:57:12)
How do we know the ratio of the space diagonal of the cube to the edge is \sqrt{3}?
RC-7th_? (19:57:26)
Pythagoreas
MCrawford (19:57:41)
Explain.
oneal3691 (19:57:41)
because that's a common rule to know
MCrawford (19:58:08)
If we understand the origins of the common rules, we are more likely to solve the harder problems.
uclabb (19:58:04)
because its rt 1+1, which is rt2, then rt 2 + 1 Pythag
uberl33tmage (19:58:12)
we have 3 sides s. sqrt(s^2+s^2+s^2)=s(sqrt 3)
kchande (19:58:09)
the side of the smaller ssquare ^2 + the diagonal of a side is 9 * sq.root 3
NoSoupForYou (19:57:48)
rt(1+rt(2)^2)
MCrawford (19:58:56)
We use a right triangle that has one cube edge and a side diagonal that connect.
MCrawford (19:59:28)
That face diagonal is on a plane perpendicular with the edge and has a vertex that creates the space diagonal.
MCrawford (19:59:40)
It's a good idea to draw this out if you've never derived it yourself.
uberl33tmage (19:59:35)
and the space diagonal is equal to 9, so we are looking for the smaller side, space diagonal:smaller side :: root3 : 1
oneal3691 (19:56:58)
so 9/rt(3) ^ 3 would be
oneal3691 (19:57:19)
739/3rt(3)
RC-7th_? (19:58:47)
The diagonal of one side of the cube is s*sqrt(2), where s is the side length. We can form a right triangle with one leg a side and the other a side diagonal. The hypotenuse is s*sqrt(3)
MCrawford (20:00:10)
Is there an easier way to calculate oneal3691's answer?
uberl33tmage (20:00:01)
which is 3 root 3
Monkey (20:00:11)
The answer is thus 81(sqrt(3)
MCrawford (20:00:29)
Dividing by \sqrt{3} before cubing seems slightly easier to me.
RC-7th_? (20:00:40)
oneal3691 made a typo, that should be 729 in the numerator
MCrawford (20:00:58)
Now, are there any other problems any of you would like to explore?
uberl33tmage (20:01:04)
Isn't it a good rule to simplify as far as you can before attempting any long functions?
MCrawford (20:01:18)
Typically, though there are exceptions.
Monkey (20:01:17)
Modular arithmetic, I suppose.
MCrawford (20:01:40)
Have a specific problem? (I rely on students for this kind of Math Jam -- I have no problems for this)
Monkey (20:01:57)
Uh, not really, so never mind...
MCrawford (20:02:25)
Okay, I have one that's on the very hard side for MATHCOUNTS modular arithmetic.
MCrawford (20:02:50)
Find all ordered pairs of integers (a, b) such that
MCrawford (20:03:00)
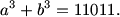
MCrawford (20:03:20)
Any ideas?
MCrawford (20:03:32)
(I'll do this one quickly -- it's just a nice exploratory problem)
Mr.Ocax (20:03:27)
factor?
Monkey (20:03:31)
Factor a^3+b^3?
sam3.14 (20:03:34)
this is probably stupid, but could we factor?
solafidefarms (20:03:34)
factorize
MCrawford (20:03:59)
That might help, but there is something specific that makes this easier.
Scrambled (20:03:36)
modulo 8?
MCrawford (20:04:24)
Searching for a good modulus in which to evaluate a number theory problem is often a good strategy.
MCrawford (20:04:33)
Here, mod 4, 8, 9 could all do the trick.
MCrawford (20:04:49)
Wait, sorry, I don't know about 4 or 8.
MCrawford (20:04:57)
But modulo 9 does.
NoSoupForYou (20:04:40)
Why?
kostya (20:04:40)
why
Mr.Ocax (20:04:42)
why?
MCrawford (20:05:11)
What are the possible residues of cubes in modulo 9?
oneal3691 (20:05:18)
what is modulo
MCrawford (20:05:56)
That's the "system" in which we're working in modular arithmetic. If you don't know modular arithmetic, it's worth asking about on the message board, though we don't have time to cover that completely here.
Mr.Ocax (20:05:34)
1, 8, 0, 1,.... ooooooooo only 3 possible
Ars_2 (20:05:39)
1,8,0
Monkey (20:05:53)
I think 1,8, and 0.
MCrawford (20:06:12)
It's easier to work with 8 as -1 in some cases.
MCrawford (20:06:17)
-1, 0, 1...
MCrawford (20:06:23)
What are the possible sums of these in pairs?
RC-7th_? (20:06:34)
0,2,-2,1,-1
MCrawford (20:06:49)
What can we now say?
RC-7th_? (20:07:02)
See what 11011 mod 9 is
uclabb (20:07:05)
11011's remainder
kostya (20:07:15)
where did 2, -2 com efrom?
MCrawford (20:07:29)
1 + 1 and -1 + (-1)
RC-7th_? (20:07:30)
11011 mod 9=4
RC-7th_? (20:07:43)
So there are no pairs!
MCrawford (20:08:08)
Sometimes a convenient modulus can tell us a lot about a number theory problem.
conartist (20:08:03)
so there are no solutions?
Mr.Ocax (20:08:05)
that's awesome
MCrawford (20:08:14)
No solutions.
RC-7th_? (20:02:44)
What is the smallest positive integer divisible by 11 which leaves a remainder of 1 when divided by 2,3,4,5,or 6?
conartist (20:08:36)
chinese remainder thereom!
Monkey (20:08:40)
Find the LCM of 2,3,4,5,and 6 first.
MCrawford (20:08:52)
I agree with Monkey.
MCrawford (20:08:56)
If you can simplify a problem -- do it.
uberl33tmage (20:08:48)
60 is the lcm
kostya (20:08:51)
60
solafidefarms (20:08:57)
60 is the LCM
NoSoupForYou (20:08:58)
60
uclabb (20:08:58)
60
MCrawford (20:09:17)
So, we're looking for a multiple of 11 that is 1 more than a multiple of 60.
solafidefarms (20:08:46)
121
kchande (20:09:09)
121
solafidefarms (20:09:27)
and then start adding multiples of 60 to 1 till you get a one divisivble by 11
MCrawford (20:09:55)
We could use the Chinese Remainder Theorem, but number sense says that we can plug and check more quickly.
georgeliu (20:09:47)
what's the Chinese remainder thereom?
MCrawford (20:10:27)
It's a method we teach in the Intro Number Theory class for solving systems of linear congruence. It would take a while to work through it here, but it's worth asking about on the message board.
solafidefarms (20:02:54)
If x is 3 mod 8, 5 mod 13, and 7 mod 9, what is the smallest value of x?
MCrawford (20:10:44)
We won't work through this one now...
MCrawford (20:10:53)
But this is a classic Chinese Remainder Theorem problem.
uberl33tmage (20:10:45)
For mathcounts problems, if you are competing, isn't it a lot more sensible to do things the short way? You only have 40 mins
MCrawford (20:11:04)
Yes, I agree...
MCrawford (20:11:25)
but, the harder problems require that you at least know how to solve the easier problems in an organized way, so it's good to practice both.
MCrawford (20:11:42)
When i competed, I did not hold to one fast rule religiously.
MCrawford (20:12:01)
I analyzed both the deeper methods and the shorter "tricks" and found the value in as much of it as I could.
uberl33tmage (20:11:58)
did you ever skip a problem and come back to it in a competition?
MCrawford (20:12:10)
Sure.
MCrawford (20:12:34)
I never worked in order -- I usually went from back to front actually, though I don't recommend that if you aren't confident you will finish any test.
Farazy (20:11:17)
Its good to know how its done though.
Farazy (20:11:30)
The idea sticks in your head a bit better.
MCrawford (20:12:48)
I agree strongly with this statement.
MCrawford (20:13:07)
There were many methods that I forgot several times until I saw "the guts" of the method.
NoSoupForYou (20:13:00)
I never skip problems. They generally get harder at the end anyway.
MCrawford (20:13:23)
I believe in skipping for a specific reason:
MCrawford (20:13:44)
I think your brain keeps working on the problem while you're not actually thinking about it.
MCrawford (20:13:49)
Then you can come back to it.
oneal3691 (20:13:23)
i do all the easy ones first
uberl33tmage (20:13:11)
If you come onto a ridiculously long question like the one we did early on a sprint round, would it likely be 0? I mean, it would take forever to solve it.
uberl33tmage (20:14:37)
I wouldn't skip too many because then you start to panic"OMG i'm not gonna finish!
Phelpedo (20:14:42)
i don't think it would necessarily be 0
MCrawford (20:15:02)
But's it's a reasonable guess -- just solve it later if not immediately.
NoSoupForYou (20:15:03)
Statistically, when a problem asks for a whole number solution, the answer is most likely 2.
MCrawford (20:15:24)
perhaps, I have no idea.
MCrawford (20:16:00)
let's move on to more problems.
Farazy (20:06:11)
oh yeah....my problem:
Suppose we have 30 foot by 63 foot room room with tiles that are 1 foot by 1 foot. If a line is drawn from one corner to an opposite corner, how many tiles does the line cross?
MCrawford (20:16:24)
How can we approach this one?
Scrambled (20:16:21)
find their gcf
MCrawford (20:16:34)
Why?
NoSoupForYou (20:16:33)
draw a diagram
uberl33tmage (20:16:19)
factor it to 10 by 21
solafidefarms (20:16:35)
It has to go over 30 vertical lines and 63 horizontal lines
uberl33tmage (20:16:43)
The tile cutting will "repeat"
MCrawford (20:17:01)
What do you mean?
Monkey (20:16:42)
Reduce the size to a 10x21.
MCrawford (20:17:29)
This is a good way to cut things up, but we'll generalize to what Scrambled mentioned.
kostya (20:16:46)
how many until it reaches an intersection
RC-7th_? (20:16:55)
But sometimes to goes over two lines at once
sam3.14 (20:17:05)
so subtract the number of lattice points
Scrambled (20:17:23)
if we anlalyze for a n/k thing where n/k is an integer, then if we multiply by k, we will get the total
uberl33tmage (20:17:31)
well, you can chop the diagram into several 10 by 21's because the line will hit a corner.
MCrawford (20:18:17)
The problem was as follows:
MCrawford (20:18:37)
We have a 30 foot by 63 foot room tiled with 1 x 1 tiles...
MCrawford (20:18:54)
If we draw a line from one corner to the other, how many tiles does it cross through?
solafidefarms (20:18:42)
So it goes throught 30+63-GCF(63,30) times that it crosses 2 lines at once, for 30+63-3=90.
uclabb (20:16:49)
93- the times it hits a vertex of four tiles
MCrawford (20:19:33)
i think of the problem this way:
MCrawford (20:19:49)
We start out on one tile and every time we hit an edge or vertex, we enter into another tile.
oneal3691 (20:20:00)
93-3
oneal3691 (20:20:03)
90
oneal3691 (20:20:06)
93-3=90
uberl33tmage (20:20:15)
It will hit every row and column
MCrawford (20:20:38)
Yes, there are 29 borders and 62 borders in the two directions.
MCrawford (20:20:57)
So, we cross 91 total borders minus the number of times we cross two at once.
oneal3691 (20:20:40)
the formulat is m+n-GCF(m,n)
uberl33tmage (20:21:00)
so you add the sides, and subtract the gcf, which is the number of times it hits an intersection, thus only entering one
MCrawford (20:21:38)
1 + (30 - 1) + (63 - 1) - (number of vertices).
MCrawford (20:21:53)
What's the number of vertices we cross between the diagonals?
NoSoupForYou (20:21:57)
3
uberl33tmage (20:22:00)
3
MCrawford (20:22:09)
No, "between"?
NoSoupForYou (20:22:13)
2
uberl33tmage (20:22:15)
2
MCrawford (20:22:25)
I hope I didn't confuse anyone.
MCrawford (20:22:42)
I started with 1 for the first tile, so in a sense I was altering the formula.
MCrawford (20:22:47)
But it works the same in the end.
MCrawford (20:22:59)
30 + 63 - gcd(30, 63) = 93 - 3 = 90.
MCrawford (20:23:34)
My calculation simplifies to this formula, but I wanted to explain from a "boundary crossing standpoint"
MCrawford (20:23:43)
Though I think we could still do that and make it nicer:
MCrawford (20:23:51)
Start outside the first vertex...
MCrawford (20:24:09)
Then consider that we "cross into the floor" through that first boundary vertex.
MCrawford (20:24:13)
Then we get
MCrawford (20:24:17)
30 + 63 boundaries
MCrawford (20:24:33)
- gcd(30, 63) where we double-counted.
oneal3691 (20:21:51)
if you didnt know this formula you could experiment with smaller grids until you figured the formula out
MCrawford (20:24:49)
I agree.
MCrawford (20:25:07)
Playing around and seeing or discovering things for yourself is by far the best way to learn problem solving math.
uberl33tmage (20:19:50)
wait so you add the number of cubes in the length and width and subtract the number of times it hits a vertex? Does that always work?
NoSoupForYou (20:25:15)
i think breaking it down into 3 10 * 21 grids is a good idea regardless of how you solve it
MCrawford (20:25:40)
NoSoupForYou's method will generalize the same way.
MCrawford (20:26:05)
And we could generalize to 3 dimensions, but the principle of inclusion-exclusion method gets a bit more complicated.
MCrawford (20:26:17)
There was an AIME problem about that which I cover in the AIME Problem Series.
MCrawford (20:26:28)
It might make for a good message board discussion to create such a problem and solve it.
Phelpedo (20:25:30)
what if the room is 30 by 30? the formula doesn't apply
MCrawford (20:26:44)
It does still apply, but it's trivialized.
MCrawford (20:26:53)
30 + 30 - 30 = 30, the correct answer.
uclabb (20:27:00)
yes it does... 30+30-30
kchande (20:27:10)
try 3 and 4
MCrawford (20:27:20)
It still works.
Phelpedo (20:27:12)
i thought there would be 59
MCrawford (20:27:39)
No, we cut a nice, symmetric diagonal through the 30 tiles on a "main diagonal".
NoSoupForYou (20:27:40)
3+4-1=6
Phelpedo (20:27:58)
is this including both diagonals?
MCrawford (20:28:13)
No, but that's a different problem.
MCrawford (20:28:21)
We were examining only one diagonal at a time.
MCrawford (20:28:43)
But the problem is nearly the same -- double it and subtract 1 if necessary.
uclabb (20:28:27)
isnt it just x2
MCrawford (20:28:57)
That depends on whether or not the diagonals cross in a common tile.
MCrawford (20:29:00)
Do they in this case?
Monkey (20:29:02)
No, because the diagonals have overlap.
MCrawford (20:29:12)
So 60 is our answer.
MCrawford (20:29:27)
But if they did, it would be 2n - 1 where n is the answer for one diagonal.
MCrawford (20:29:39)
That is all the time we have for tonight's Math Jam.
MCrawford (20:29:44)
I hope you enjoyed it.
Phelpedo (20:29:41)
but for a square, the diagonals to intersect
MCrawford (20:30:07)
The point is that they don't intersect in the interior of a tile -- they intersect on a vertex in some cases.
sam3.14 (20:29:45)
Thanks a lot!
uclabb (20:29:46)
thanks
oneal3691 (20:29:46)
ok
NoSoupForYou (20:30:23)
thanks
RC-7th_? (20:30:24)
Thanks!
Monkey (20:30:31)
Thanks, Mr.Crawford!
kostya (20:30:31)
[b][i]Thanks! Bye-bye![/i][/b]
uclabb (20:30:38)
who here is going to national?
Monkey (20:30:59)
Me.
Phelpedo (20:31:01)
i'm going
ln(dx/dy)_2 (20:31:03)
not me
kchande (20:31:07)
me
oneal3691 (20:31:08)
me
NoSoupForYou (20:31:14)
i'm going
uberl33tmage (20:31:14)
I am![img id=em-0]
RC-7th_? (20:31:15)
me
uclabb (20:31:17)
I came short by two points
uberl33tmage (20:31:17)
ME!
oneal3691 (20:31:19)
thanks mr crawford
solafidefarms (20:31:23)
I am going to nats!
sam3.14 (20:31:26)
I wish I had been more into extracurricular math in middle school
MCrawford (20:31:53)
It's never a bad time to start learning more problem solving math.
If two positive integers m and n satisfy 1/m+1/n=1/15, then what is the least m+n could be?
Mr.Ocax (19:21:40)
something like that of course, i'd also like to know how to do all problems in that format
MCrawford (19:29:12)
Our first problem is a number theory problem.
MCrawford (19:29:18)
What is difficult about this problem?
RC-7th_? (19:29:31)
Fractions
Monkey (19:29:37)
There are two variables, but only one equation.
MCrawford (19:29:51)
How might we begin dealing with these difficulties?
NoSoupForYou (19:29:59)
multiply by mn
sam3.14 (19:30:02)
multiply by common denom
RC-7th_? (19:30:03)
multiply through by mn?
MCrawford (19:30:40)
I would go one step farther and multiply by 15mn to clear all the denominators.
solafidefarms (19:30:38)
The common denominator is 15mn
MCrawford (19:30:55)
What do we get when we multiply out the denominators?
RC-7th_? (19:31:06)
15m+15n=mn
Mr.Ocax (19:31:09)
so 15(n+m)=mn?
NoSoupForYou (19:31:11)
15(m+n)=mn
oneal3691 (19:31:15)
15n+15m=mn
MCrawford (19:31:30)
Now we have an equation that looks easier to work with, but it still involves two variables.
MCrawford (19:31:38)
What could we do at this point?
solafidefarms (19:31:46)
factor?
MCrawford (19:32:05)
How could we factor?
RC-7th_? (19:32:08)
Move them over, and simon's favorite factoring trick?
Mr.Ocax (19:31:33)
(m-15)(n-15)=-225?
Mr.Ocax (19:31:45)
woops that's a 225
MCrawford (19:32:39)
We first stick everything on one side:
MCrawford (19:32:44)
mn - 15m - 15n = 0.
Mr.Ocax (19:32:34)
whats simon's fav factoring trick? i've heard all about it
Mr.Ocax (19:32:17)
add 225 to both sides?
MCrawford (19:33:09)
I suggest doing a search for it on the forums -- you'll see many great and insightful examples.
MCrawford (19:33:16)
But we'll finish this problem using it.
NoSoupForYou (19:33:13)
who's simon
MCrawford (19:33:31)
ComplexZeta on AoPS -- a great student of mathematics.
solafidefarms (19:33:10)
mn-m-n-1=0=> (m-1)(n-1)=0
MCrawford (19:34:06)
Simon's favorite factoring trick reminds us that we can take a product along with a linear combination of two variables and create a factorization.
MCrawford (19:34:17)
mn + m + n + 1 = (m + 1)(n + 1) for instance
MCrawford (19:34:32)
Here we want something in the form
MCrawford (19:34:39)
(m - something)(n - something)
MCrawford (19:34:55)
Clearly each "something" must be 15 in this case so that we get
MCrawford (19:35:04)
mn - 15m - 15n as part of our expression.
MCrawford (19:35:13)
But, we must do something to our equation.
Monkey (19:34:23)
For the sum of m and n to be as small as possible, then m-15 and n-15 have to be as close as possible to each other, and still multiply to 225.
solafidefarms (19:35:03)
(m-15)(n-15)=225
MCrawford (19:35:31)
We had to add 225, the product (-15)(-15)
Mr.Ocax (19:34:35)
ok i found it on the forum, very helpful
Mr.Ocax (19:31:56)
ahh.. and then use the factors of 225 to find m and n, ok
MCrawford (19:35:44)
Exactly!
MCrawford (19:36:01)
We manipulated our single equation into a form that allows us to apply what we know about integers.
MCrawford (19:36:11)
Hence the number theory aspect of the problem.
uclabb (19:29:29)
60
Mr.Ocax (19:33:02)
so would the answer be 60?
Monkey (19:35:44)
Thus, m and n are each 30, so the sum of them is 60
MCrawford (19:36:33)
How do we know these give us the smallest possible?
RC-7th_? (19:36:09)
Notice that this tells us that (m,n)=(0,0) is okay, but it obviously isn't
MCrawford (19:37:13)
Right -- we need positive integers.
Monkey (19:37:23)
Because they give 15x15=225 in our nice factored equation, and 15 and 15 are as close as possible to each other.
oneal3691 (19:37:23)
can m and n be the same?
MCrawford (19:37:51)
Unless it says "distinct integers", yes, they can be the same.
conartist (19:37:49)
because the extreme factors are larger than those that are closer together: if we have 225 and 1, then our sums are greater than if we have 15 and 15
uclabb (19:38:13)
just like for ab= 64. The lowest a + b can be is 16 (8 + 8)
sam3.14 (19:37:06)
if mn=k, then m+n is minimized when m is closest to n
MCrawford (19:38:38)
Why does this work?
RC-7th_? (19:38:51)
It's based on (a+b)(a-b)=a^2-b^2
MCrawford (19:39:06)
That's one way to do it.
MCrawford (19:39:29)
If the sum of two numbers is 2a, then the largest product is made by setting b equal to 0.
MCrawford (19:39:32)
Conversely...
MCrawford (19:40:17)
A higher sum could always make a higher product, so we still want a + b and a - b to be as close together as possible.
Monkey (19:39:22)
I'm not sure, but it might also work because of the AM-GM inequality.
MCrawford (19:40:36)
For those of you who are familiar with inequalities, this is another good solution.
MCrawford (19:40:57)
The arithmetic mean of a group of nonnegative real numbers is at least as large as their geometric mean.
MCrawford (19:41:10)
The only time equality occurs is when all variables are set equal.
ln(dx/dy)_2 (19:40:50)
What does AM-GM stand for?
MCrawford (19:41:25)
arithmetic mean-geometric mean inequality.
sam3.14 (19:40:43)
Ooh. We can do this with rectangle areas. If the area of a rectangle is fixed, then a square has the smallest perimeter
MCrawford (19:41:51)
True -- and we can use variables just like RC-7th did to make this leap to the geometric analogy!
oneal3691 (19:39:03)
think of it as squares and rectangles and the area of them
NoSoupForYou (19:38:47)
If 1/m+1/n=1/a, would m=a/2 and b/2 always give the greatest possible value for (m + n)?
MCrawford (19:42:23)
I think you mean m = 2a nd n = 2a.
NoSoupForYou (19:42:36)
yeah
MCrawford (19:42:44)
And yes, if you work out the algebra, so long as a is an integer, this will work out.
Mr.Ocax (19:43:03)
what if the number on top of a is a number other than 1?
Mr.Ocax (19:23:34)
Given the equation 1/m+1/n=2/15, where m and n are positive integers, find the value of m+n such that m>n and m is not a mulitple of n.
MCrawford (19:43:27)
Then you're back to working with Simon's favorite factoring trick.
MCrawford (19:43:40)
Let's take a brief review of the most important problem solving concepts here.
MCrawford (19:43:50)
First, we identified the difficulties with the given equation.
MCrawford (19:44:12)
This is extremely important in problem solving as it often gives us a clue as to what steps or tools we might apply.
MCrawford (19:44:33)
Identifying the fractions as a difficulty immediately helps us as we can multiply them away and see if that works:
solafidefarms (19:43:40)
15m+15n=2mn...
MCrawford (19:45:07)
Simon's favorite factoring trick might be a little harder to provoke here because the factorization is going to be harder to create.
Monkey (19:44:52)
Then get all the stuff to one side and factor again...
Mr.Ocax (19:45:03)
and divide by 2 to make factoring easier?
RC-7th_? (19:45:11)
56.25=2(m-7.5)(n-7.5)=>225=2(2m-15)(2n-15)
MCrawford (19:45:44)
Great work. So, what are the possible integers m and n?
kostya (19:45:42)
fractions is what you get
MCrawford (19:45:56)
How do you mean?
kostya (19:46:34)
I mean that if you divide by 2, you'l get fractoins for some time
MCrawford (19:46:52)
So there are no integer solutions.
Mr.Ocax (19:46:58)
they are each 15 aren't they?
MCrawford (19:47:10)
Hmmm, you're right -- where did we go wrong?
MCrawford (19:47:26)
I see the problem.
MCrawford (19:47:41)
RC-7th needed to add 2 * 56.25 to both sides.
MCrawford (19:48:04)
So we should have had 225 = (2m - 15)(2n-15)
MCrawford (19:48:09)
Sorry, I missed that.
Mr.Ocax (19:47:57)
my factorization was (m-7.5)(n-7.5)=56.25
MCrawford (19:48:27)
Yes, that multiplied by 4 gives the right idea.
Mr.Ocax (19:48:24)
so the next closest is m-15/2=45/2 and n-15/2=5/2, so m=30 and n=10
MCrawford (19:49:30)
Hmmm, 25*9 = 225
MCrawford (19:49:37)
I think this makes closer factors.
MCrawford (19:49:45)
But we should move on so that we can look at other problems.
uclabb (19:46:08)
What is the probability that a factor of 15^40 is a multiple of 15^25?
Farazy (19:48:39)
Wouldn't Greedy's Algorithm be quicker?
Farazy (19:49:44)
Greedy's algorithm says find the highest fraction with one in the numerator and subtract from what you want as your result.
MCrawford (19:50:02)
We'll work uclabb's problem.
MCrawford (19:50:17)
How can we examine this problem?
uberl33tmage (19:50:22)
We have 41*41 factors iin 15^40
Monkey (19:50:28)
First factor 15^40 into primes.
sam3.14 (19:50:42)
we should do the prime factorization of each number, I think
MCrawford (19:51:05)
We use prime factorization to organize information about integers.
MCrawford (19:51:19)
It is extremely important not to view this as a formulaic process.
MCrawford (19:51:36)
What must the prime factorization of 15^40 look like?
Farazy (19:51:50)
3^40*5^40
Monkey (19:51:51)
3^40x5^40
solafidefarms (19:51:51)
3^40 5^40
MCrawford (19:52:16)
Sorry, I meant to ask, "what must the prime factorization of a divisor of 15^40 look like?"
NoSoupForYou (19:52:31)
3^a*5^b
Monkey (19:52:38)
3^nx5^m
solafidefarms (19:52:40)
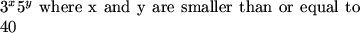
sam3.14 (19:52:43)
3^n 5^m , m,n <= 40
MCrawford (19:52:54)
Each exponent can be from 0 to 40.
MCrawford (19:53:04)
That's why we get 41*41 total divisors.
MCrawford (19:53:10)
Now what?
RC-7th_? (19:50:25)
Find the total number of factors, and find which are multiples
uberl33tmage (19:52:50)
3^(x>or= to 25) *5^(y>or=to 25)
Mr.Ocax (19:53:15)
but because you want a multiple of 15^25,the exponents have to be larger
MCrawford (19:53:38)
*at least as large as 25, but no larger than 40.
RC-7th_? (19:53:36)
16*16 are the number of divisors which are also mulitples
oneal3691 (19:51:00)
so we have 41^2 factors in the first
Monkey (19:53:08)
Which means there are 1681 factors.
uberl33tmage (19:53:47)
there are 16 integes between 25 and 40 inclusive. we have 16*16 successes out of 41*41 total, so our chances are 256/1681
uclabb (19:53:50)
41^2 = 1681, the denominater
uberl33tmage (19:51:33)
there are 16 factors for 3 and 5, As long as the power is more than or equal to 25, we have a success. The probability is (16/41)^2
MCrawford (19:54:21)
That is indeed the probability that a divisor of 15^40 is a multiple of 15^25.
MCrawford (19:54:45)
Remember, in hard divisor problems, prime factorization provides you with the organization for the information that you need.
MCrawford (19:55:02)
If you view divisor problems this way, they often turn into much simpler counting problems.
MCrawford (19:55:17)
Let's look at a geometry problem next.
E^(pi*i)=-1 (19:49:52)
A sphere is inscribed in a cube with side length 9 inches. Then, a smaller cube is inscribed in the sphere. How many cubic inches are in the volume of the inscibed cube?
MCrawford (19:55:34)
What do we need to do with this one?
Mr.Ocax (19:55:35)
make this a 2d problem
MCrawford (19:55:46)
That could help.
MCrawford (19:56:00)
But I think that might actually make this problem harder to think about.
MCrawford (19:56:06)
For a specific reason.
MCrawford (19:56:14)
(but it's often a good idea with 3-D problems)
oneal3691 (19:56:05)
the diameter of the sphere would be 9
Monkey (19:55:59)
Find the radius of the sphere first (which is easy).
Scrambled (19:55:54)
establish sides in terms of the largest radius
oneal3691 (19:56:13)
which would be the space diagonal of the cube
uberl33tmage (19:56:04)
The space diagonal of the smaller cube is equal to a side of the big cube.
oneal3691 (19:56:18)
or 9/rt(3)
Monkey (19:56:23)
Because a radius of the sphere is the space diagonal of the inner cube.
sam3.14 (19:56:23)
the internal diagonal of the smaller square is equal to the diameter of the sphere
uberl33tmage (19:56:41)
the ratio is 1 to root 3
MCrawford (19:57:12)
How do we know the ratio of the space diagonal of the cube to the edge is \sqrt{3}?
RC-7th_? (19:57:26)
Pythagoreas
MCrawford (19:57:41)
Explain.
oneal3691 (19:57:41)
because that's a common rule to know
MCrawford (19:58:08)
If we understand the origins of the common rules, we are more likely to solve the harder problems.
uclabb (19:58:04)
because its rt 1+1, which is rt2, then rt 2 + 1 Pythag
uberl33tmage (19:58:12)
we have 3 sides s. sqrt(s^2+s^2+s^2)=s(sqrt 3)
kchande (19:58:09)
the side of the smaller ssquare ^2 + the diagonal of a side is 9 * sq.root 3
NoSoupForYou (19:57:48)
rt(1+rt(2)^2)
MCrawford (19:58:56)
We use a right triangle that has one cube edge and a side diagonal that connect.
MCrawford (19:59:28)
That face diagonal is on a plane perpendicular with the edge and has a vertex that creates the space diagonal.
MCrawford (19:59:40)
It's a good idea to draw this out if you've never derived it yourself.
uberl33tmage (19:59:35)
and the space diagonal is equal to 9, so we are looking for the smaller side, space diagonal:smaller side :: root3 : 1
oneal3691 (19:56:58)
so 9/rt(3) ^ 3 would be
oneal3691 (19:57:19)
739/3rt(3)
RC-7th_? (19:58:47)
The diagonal of one side of the cube is s*sqrt(2), where s is the side length. We can form a right triangle with one leg a side and the other a side diagonal. The hypotenuse is s*sqrt(3)
MCrawford (20:00:10)
Is there an easier way to calculate oneal3691's answer?
uberl33tmage (20:00:01)
which is 3 root 3
Monkey (20:00:11)
The answer is thus 81(sqrt(3)
MCrawford (20:00:29)
Dividing by \sqrt{3} before cubing seems slightly easier to me.
RC-7th_? (20:00:40)
oneal3691 made a typo, that should be 729 in the numerator
MCrawford (20:00:58)
Now, are there any other problems any of you would like to explore?
uberl33tmage (20:01:04)
Isn't it a good rule to simplify as far as you can before attempting any long functions?
MCrawford (20:01:18)
Typically, though there are exceptions.
Monkey (20:01:17)
Modular arithmetic, I suppose.
MCrawford (20:01:40)
Have a specific problem? (I rely on students for this kind of Math Jam -- I have no problems for this)
Monkey (20:01:57)
Uh, not really, so never mind...
MCrawford (20:02:25)
Okay, I have one that's on the very hard side for MATHCOUNTS modular arithmetic.
MCrawford (20:02:50)
Find all ordered pairs of integers (a, b) such that
MCrawford (20:03:00)
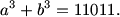
MCrawford (20:03:20)
Any ideas?
MCrawford (20:03:32)
(I'll do this one quickly -- it's just a nice exploratory problem)
Mr.Ocax (20:03:27)
factor?
Monkey (20:03:31)
Factor a^3+b^3?
sam3.14 (20:03:34)
this is probably stupid, but could we factor?
solafidefarms (20:03:34)
factorize
MCrawford (20:03:59)
That might help, but there is something specific that makes this easier.
Scrambled (20:03:36)
modulo 8?
MCrawford (20:04:24)
Searching for a good modulus in which to evaluate a number theory problem is often a good strategy.
MCrawford (20:04:33)
Here, mod 4, 8, 9 could all do the trick.
MCrawford (20:04:49)
Wait, sorry, I don't know about 4 or 8.
MCrawford (20:04:57)
But modulo 9 does.
NoSoupForYou (20:04:40)
Why?
kostya (20:04:40)
why
Mr.Ocax (20:04:42)
why?
MCrawford (20:05:11)
What are the possible residues of cubes in modulo 9?
oneal3691 (20:05:18)
what is modulo
MCrawford (20:05:56)
That's the "system" in which we're working in modular arithmetic. If you don't know modular arithmetic, it's worth asking about on the message board, though we don't have time to cover that completely here.
Mr.Ocax (20:05:34)
1, 8, 0, 1,.... ooooooooo only 3 possible
Ars_2 (20:05:39)
1,8,0
Monkey (20:05:53)
I think 1,8, and 0.
MCrawford (20:06:12)
It's easier to work with 8 as -1 in some cases.
MCrawford (20:06:17)
-1, 0, 1...
MCrawford (20:06:23)
What are the possible sums of these in pairs?
RC-7th_? (20:06:34)
0,2,-2,1,-1
MCrawford (20:06:49)
What can we now say?
RC-7th_? (20:07:02)
See what 11011 mod 9 is
uclabb (20:07:05)
11011's remainder
kostya (20:07:15)
where did 2, -2 com efrom?
MCrawford (20:07:29)
1 + 1 and -1 + (-1)
RC-7th_? (20:07:30)
11011 mod 9=4
RC-7th_? (20:07:43)
So there are no pairs!
MCrawford (20:08:08)
Sometimes a convenient modulus can tell us a lot about a number theory problem.
conartist (20:08:03)
so there are no solutions?
Mr.Ocax (20:08:05)
that's awesome
MCrawford (20:08:14)
No solutions.
RC-7th_? (20:02:44)
What is the smallest positive integer divisible by 11 which leaves a remainder of 1 when divided by 2,3,4,5,or 6?
conartist (20:08:36)
chinese remainder thereom!
Monkey (20:08:40)
Find the LCM of 2,3,4,5,and 6 first.
MCrawford (20:08:52)
I agree with Monkey.
MCrawford (20:08:56)
If you can simplify a problem -- do it.
uberl33tmage (20:08:48)
60 is the lcm
kostya (20:08:51)
60
solafidefarms (20:08:57)
60 is the LCM
NoSoupForYou (20:08:58)
60
uclabb (20:08:58)
60
MCrawford (20:09:17)
So, we're looking for a multiple of 11 that is 1 more than a multiple of 60.
solafidefarms (20:08:46)
121
kchande (20:09:09)
121
solafidefarms (20:09:27)
and then start adding multiples of 60 to 1 till you get a one divisivble by 11
MCrawford (20:09:55)
We could use the Chinese Remainder Theorem, but number sense says that we can plug and check more quickly.
georgeliu (20:09:47)
what's the Chinese remainder thereom?
MCrawford (20:10:27)
It's a method we teach in the Intro Number Theory class for solving systems of linear congruence. It would take a while to work through it here, but it's worth asking about on the message board.
solafidefarms (20:02:54)
If x is 3 mod 8, 5 mod 13, and 7 mod 9, what is the smallest value of x?
MCrawford (20:10:44)
We won't work through this one now...
MCrawford (20:10:53)
But this is a classic Chinese Remainder Theorem problem.
uberl33tmage (20:10:45)
For mathcounts problems, if you are competing, isn't it a lot more sensible to do things the short way? You only have 40 mins
MCrawford (20:11:04)
Yes, I agree...
MCrawford (20:11:25)
but, the harder problems require that you at least know how to solve the easier problems in an organized way, so it's good to practice both.
MCrawford (20:11:42)
When i competed, I did not hold to one fast rule religiously.
MCrawford (20:12:01)
I analyzed both the deeper methods and the shorter "tricks" and found the value in as much of it as I could.
uberl33tmage (20:11:58)
did you ever skip a problem and come back to it in a competition?
MCrawford (20:12:10)
Sure.
MCrawford (20:12:34)
I never worked in order -- I usually went from back to front actually, though I don't recommend that if you aren't confident you will finish any test.
Farazy (20:11:17)
Its good to know how its done though.
Farazy (20:11:30)
The idea sticks in your head a bit better.
MCrawford (20:12:48)
I agree strongly with this statement.
MCrawford (20:13:07)
There were many methods that I forgot several times until I saw "the guts" of the method.
NoSoupForYou (20:13:00)
I never skip problems. They generally get harder at the end anyway.
MCrawford (20:13:23)
I believe in skipping for a specific reason:
MCrawford (20:13:44)
I think your brain keeps working on the problem while you're not actually thinking about it.
MCrawford (20:13:49)
Then you can come back to it.
oneal3691 (20:13:23)
i do all the easy ones first
uberl33tmage (20:13:11)
If you come onto a ridiculously long question like the one we did early on a sprint round, would it likely be 0? I mean, it would take forever to solve it.
uberl33tmage (20:14:37)
I wouldn't skip too many because then you start to panic"OMG i'm not gonna finish!
Phelpedo (20:14:42)
i don't think it would necessarily be 0
MCrawford (20:15:02)
But's it's a reasonable guess -- just solve it later if not immediately.
NoSoupForYou (20:15:03)
Statistically, when a problem asks for a whole number solution, the answer is most likely 2.
MCrawford (20:15:24)
perhaps, I have no idea.
MCrawford (20:16:00)
let's move on to more problems.
Farazy (20:06:11)
oh yeah....my problem:
Suppose we have 30 foot by 63 foot room room with tiles that are 1 foot by 1 foot. If a line is drawn from one corner to an opposite corner, how many tiles does the line cross?
MCrawford (20:16:24)
How can we approach this one?
Scrambled (20:16:21)
find their gcf
MCrawford (20:16:34)
Why?
NoSoupForYou (20:16:33)
draw a diagram
uberl33tmage (20:16:19)
factor it to 10 by 21
solafidefarms (20:16:35)
It has to go over 30 vertical lines and 63 horizontal lines
uberl33tmage (20:16:43)
The tile cutting will "repeat"
MCrawford (20:17:01)
What do you mean?
Monkey (20:16:42)
Reduce the size to a 10x21.
MCrawford (20:17:29)
This is a good way to cut things up, but we'll generalize to what Scrambled mentioned.
kostya (20:16:46)
how many until it reaches an intersection
RC-7th_? (20:16:55)
But sometimes to goes over two lines at once
sam3.14 (20:17:05)
so subtract the number of lattice points
Scrambled (20:17:23)
if we anlalyze for a n/k thing where n/k is an integer, then if we multiply by k, we will get the total
uberl33tmage (20:17:31)
well, you can chop the diagram into several 10 by 21's because the line will hit a corner.
MCrawford (20:18:17)
The problem was as follows:
MCrawford (20:18:37)
We have a 30 foot by 63 foot room tiled with 1 x 1 tiles...
MCrawford (20:18:54)
If we draw a line from one corner to the other, how many tiles does it cross through?
solafidefarms (20:18:42)
So it goes throught 30+63-GCF(63,30) times that it crosses 2 lines at once, for 30+63-3=90.
uclabb (20:16:49)
93- the times it hits a vertex of four tiles
MCrawford (20:19:33)
i think of the problem this way:
MCrawford (20:19:49)
We start out on one tile and every time we hit an edge or vertex, we enter into another tile.
oneal3691 (20:20:00)
93-3
oneal3691 (20:20:03)
90
oneal3691 (20:20:06)
93-3=90
uberl33tmage (20:20:15)
It will hit every row and column
MCrawford (20:20:38)
Yes, there are 29 borders and 62 borders in the two directions.
MCrawford (20:20:57)
So, we cross 91 total borders minus the number of times we cross two at once.
oneal3691 (20:20:40)
the formulat is m+n-GCF(m,n)
uberl33tmage (20:21:00)
so you add the sides, and subtract the gcf, which is the number of times it hits an intersection, thus only entering one
MCrawford (20:21:38)
1 + (30 - 1) + (63 - 1) - (number of vertices).
MCrawford (20:21:53)
What's the number of vertices we cross between the diagonals?
NoSoupForYou (20:21:57)
3
uberl33tmage (20:22:00)
3
MCrawford (20:22:09)
No, "between"?
NoSoupForYou (20:22:13)
2
uberl33tmage (20:22:15)
2
MCrawford (20:22:25)
I hope I didn't confuse anyone.
MCrawford (20:22:42)
I started with 1 for the first tile, so in a sense I was altering the formula.
MCrawford (20:22:47)
But it works the same in the end.
MCrawford (20:22:59)
30 + 63 - gcd(30, 63) = 93 - 3 = 90.
MCrawford (20:23:34)
My calculation simplifies to this formula, but I wanted to explain from a "boundary crossing standpoint"
MCrawford (20:23:43)
Though I think we could still do that and make it nicer:
MCrawford (20:23:51)
Start outside the first vertex...
MCrawford (20:24:09)
Then consider that we "cross into the floor" through that first boundary vertex.
MCrawford (20:24:13)
Then we get
MCrawford (20:24:17)
30 + 63 boundaries
MCrawford (20:24:33)
- gcd(30, 63) where we double-counted.
oneal3691 (20:21:51)
if you didnt know this formula you could experiment with smaller grids until you figured the formula out
MCrawford (20:24:49)
I agree.
MCrawford (20:25:07)
Playing around and seeing or discovering things for yourself is by far the best way to learn problem solving math.
uberl33tmage (20:19:50)
wait so you add the number of cubes in the length and width and subtract the number of times it hits a vertex? Does that always work?
NoSoupForYou (20:25:15)
i think breaking it down into 3 10 * 21 grids is a good idea regardless of how you solve it
MCrawford (20:25:40)
NoSoupForYou's method will generalize the same way.
MCrawford (20:26:05)
And we could generalize to 3 dimensions, but the principle of inclusion-exclusion method gets a bit more complicated.
MCrawford (20:26:17)
There was an AIME problem about that which I cover in the AIME Problem Series.
MCrawford (20:26:28)
It might make for a good message board discussion to create such a problem and solve it.
Phelpedo (20:25:30)
what if the room is 30 by 30? the formula doesn't apply
MCrawford (20:26:44)
It does still apply, but it's trivialized.
MCrawford (20:26:53)
30 + 30 - 30 = 30, the correct answer.
uclabb (20:27:00)
yes it does... 30+30-30
kchande (20:27:10)
try 3 and 4
MCrawford (20:27:20)
It still works.
Phelpedo (20:27:12)
i thought there would be 59
MCrawford (20:27:39)
No, we cut a nice, symmetric diagonal through the 30 tiles on a "main diagonal".
NoSoupForYou (20:27:40)
3+4-1=6
Phelpedo (20:27:58)
is this including both diagonals?
MCrawford (20:28:13)
No, but that's a different problem.
MCrawford (20:28:21)
We were examining only one diagonal at a time.
MCrawford (20:28:43)
But the problem is nearly the same -- double it and subtract 1 if necessary.
uclabb (20:28:27)
isnt it just x2
MCrawford (20:28:57)
That depends on whether or not the diagonals cross in a common tile.
MCrawford (20:29:00)
Do they in this case?
Monkey (20:29:02)
No, because the diagonals have overlap.
MCrawford (20:29:12)
So 60 is our answer.
MCrawford (20:29:27)
But if they did, it would be 2n - 1 where n is the answer for one diagonal.
MCrawford (20:29:39)
That is all the time we have for tonight's Math Jam.
MCrawford (20:29:44)
I hope you enjoyed it.
Phelpedo (20:29:41)
but for a square, the diagonals to intersect
MCrawford (20:30:07)
The point is that they don't intersect in the interior of a tile -- they intersect on a vertex in some cases.
sam3.14 (20:29:45)
Thanks a lot!
uclabb (20:29:46)
thanks
oneal3691 (20:29:46)
ok
NoSoupForYou (20:30:23)
thanks
RC-7th_? (20:30:24)
Thanks!
Monkey (20:30:31)
Thanks, Mr.Crawford!
kostya (20:30:31)
[b][i]Thanks! Bye-bye![/i][/b]
uclabb (20:30:38)
who here is going to national?
Monkey (20:30:59)
Me.
Phelpedo (20:31:01)
i'm going
ln(dx/dy)_2 (20:31:03)
not me
kchande (20:31:07)
me
oneal3691 (20:31:08)
me
NoSoupForYou (20:31:14)
i'm going
uberl33tmage (20:31:14)
I am![img id=em-0]
RC-7th_? (20:31:15)
me
uclabb (20:31:17)
I came short by two points
uberl33tmage (20:31:17)
ME!
oneal3691 (20:31:19)
thanks mr crawford
solafidefarms (20:31:23)
I am going to nats!
sam3.14 (20:31:26)
I wish I had been more into extracurricular math in middle school
MCrawford (20:31:53)
It's never a bad time to start learning more problem solving math.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









